Полиномиальная множественная регрессионная модель Мультипликативная регрессионная модель Обратная

Полиномиальная множественная регрессионная модель Мультипликативная регрессионная модель Обратная регрессионная модель Экспоненциальная модель

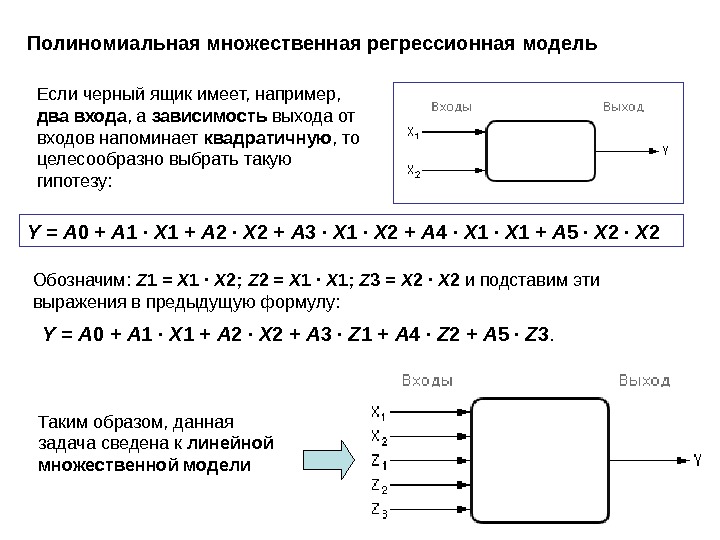
Полиномиальная множественная регрессионная модель Если черный ящик имеет, например, два входа , а зависимость выхода от входов напоминает квадратичную , то целесообразно выбрать такую гипотезу: Y = A 0 + A 1 · X 1 + A 2 · X 2 + A 3 · X 1 · X 2 + A 4 · X 1 + A 5 · X 2 Обозначим: Z 1 = X 1 · X 2; Z 2 = X 1 · X 1; Z 3 = X 2 · X 2 и подставим эти выражения в предыдущую формулу: Y = A 0 + A 1 · X 1 + A 2 · X 2 + A 3 · Z 1 + A 4 · Z 2 + A 5 · Z 3. Таким образом, данная задача сведена к линейной множественной модели

Мультипликативная регрессионная модель Прологарифмируем левую и правую части данного уравнения: ln( Y ) = ln( A 0) + A 1 · ln( X 1) + A 2 · ln( X 2) + … + Am · ln( Xm ). Обозначим : W = ln( Y ), B 0 = ln( A 0), Z 1 = ln( X 1), Z 2 = ln( X 2), …, Zm = ln( Xm ). Получим : W = B 0 + A 1 · Z 1 + A 2 · Z 2 + … + Am · Zm. То есть вновь осуществлен переход к линейной множественной модели. m. A m AA XXXAY*. . ***

Обратная регрессионная модельmm. XAXAA k Y *. . . *110 Заменим: W = 1/ Y , ai = Ai / k. И перейдем к линейной множественной модели W = a 0 + a 1 · X 1 + … + am · Xm.

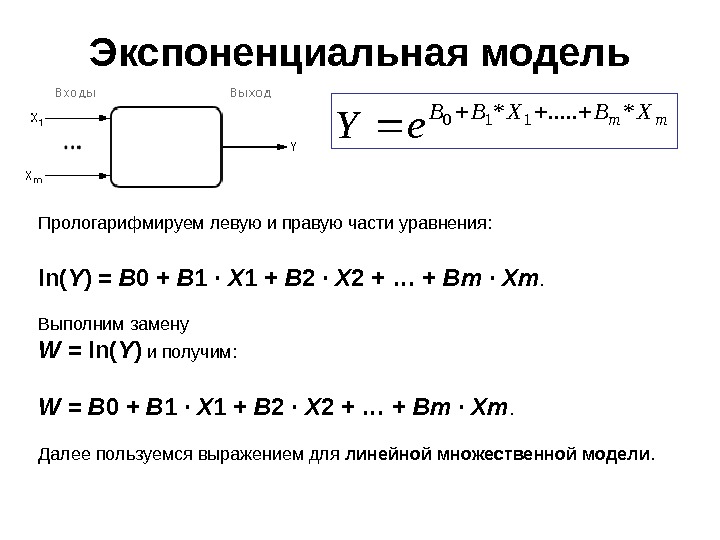
Экспоненциальная модельmm. XBXBB e. Y *. . . *110 Прологарифмируем левую и правую части уравнения: ln( Y ) = B 0 + B 1 · X 1 + B 2 · X 2 + … + Bm · Xm. Выполним замену W = ln( Y ) и получим: W = B 0 + B 1 · X 1 + B 2 · X 2 + … + Bm · Xm. Далее пользуемся выражением для линейной множественной модели.

Регрессионный анализ нелинейной модели Получены экспериментальные данные: Y 6 13, 5 24 37, 5 54 73, 5 X 2 3 4 5 6 7 По виду график похож на степенную функцию Y=a 0 a 1 x b + Для нахождения коэффициентов уравнения применим метод линеаризации, для этого прологарифмируем функцию и сделаем подстановку. L g y = L g a 0 L g a 1 + L g b x + Y=Lgy, A 0=Lga 0 Lga 1, A 1 + =Lgb Y=A 0 A 1 x + Построим новую табличную зависимость с учетом подстановки. y 6 13, 5 24 37, 5 54 73, 5 Y=Lgy 0. 778 1. 13 1. 38 1. 574 1. 732 1. 866 x 2 3 4 5 6 7 Y=Lgy, A 0=Lga 0 Lga 1, A 1 + =Lgb A 0 A 12 + =0, 778 A 0 A 17 + =1, 866 Решаем данную систему уравнений и находим значение коэффициент A 0 = 0 , 3 4 2 8 A 1 = 0 , 2 1 7 6 A 0=Lga 0 Lga 1, A 1 + =Lgb По виду зависимости предполагаем, что она проходит через ноль, следовательно a 0=0 A 0 = L g a 1 , a 1 = 1 0 0 , 3 4 2 8 b = 1 0 0, 2176 a 1=2, 2 b=1, 65 y=2, 2 x 1, 65 Y=a 0 a 1 x b +

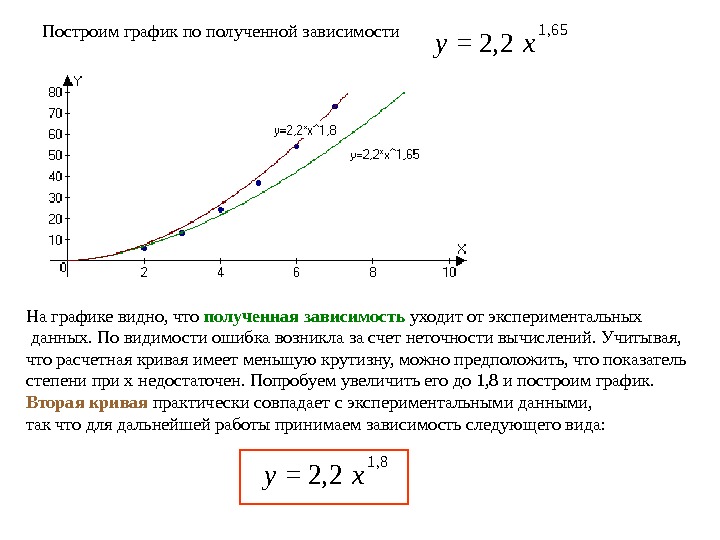
Построим график по полученной зависимости y=2, 2 x 1 , 6 5 На графике видно, что полученная зависимость уходит от экспериментальных данных. По видимости ошибка возникла за счет неточности вычислений. Учитывая, что расчетная кривая имеет меньшую крутизну, можно предположить, что показатель степени при х недостаточен. Попробуем увеличить его до 1, 8 и построим график. Вторая кривая практически совпадает с экспериментальными данными, так что для дальнейшей работы принимаем зависимость следующего вида: y=2, 2 x 1,

The end