Подземная гидромеханика — это наука о движе-нии нефти,





























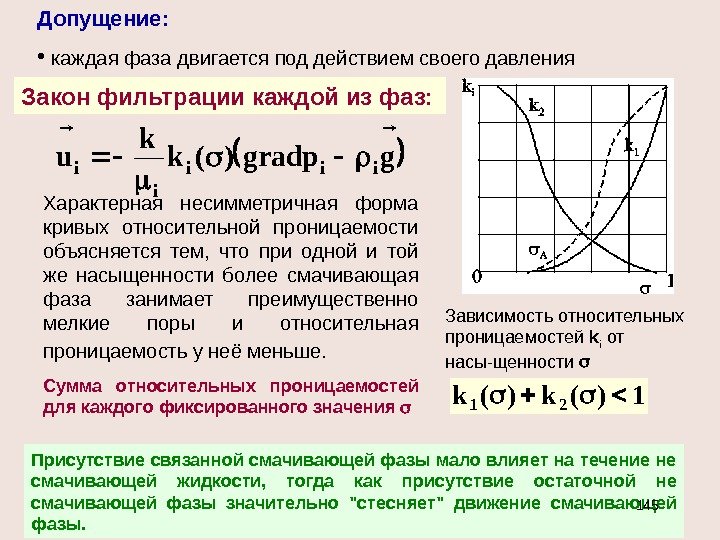
![Замыкающие соотношения [ , m, k, μ =f(p)] Зависимость плотности от Замыкающие соотношения [ , m, k, μ =f(p)] Зависимость плотности от](http://present5.com/presentforday2/20170114/pgm_prezent_images/pgm_prezent_44.jpg)




































































































































pgm_prezent.ppt
- Размер: 4.5 Мб
- Автор: Ivan Chistyakov
- Количество слайдов: 228
Описание презентации Подземная гидромеханика — это наука о движе-нии нефти, по слайдам
 Подземная гидромеханика — это наука о движе-нии нефти, воды, газа и их смесей в пористых и трещиновато-пористых горных породах, слагающих продуктивные пласты и массивы. Основу подземной гидромеханики составляет теория фильтрации, а сама наука является теоретической основой разработки нефтяных, газовых и газоконденсатных месторождений. Лектор: профессор Квеско Брониславович
Подземная гидромеханика — это наука о движе-нии нефти, воды, газа и их смесей в пористых и трещиновато-пористых горных породах, слагающих продуктивные пласты и массивы. Основу подземной гидромеханики составляет теория фильтрации, а сама наука является теоретической основой разработки нефтяных, газовых и газоконденсатных месторождений. Лектор: профессор Квеско Брониславович
 2 Разработка залежи — это вызов процесса движения пластовых жидкостей и управление его дальнейшим течением с помощью скважин. Система разработки залежи должна обеспечивать: а) заданный уровень добычи нефти или газа; б) минимум затрат; в) возможно более полное извлечение нефти или газа. Такая система является рациональной. Установление рациональной системы разработки путем промыслового эксперимента невозможно.
2 Разработка залежи — это вызов процесса движения пластовых жидкостей и управление его дальнейшим течением с помощью скважин. Система разработки залежи должна обеспечивать: а) заданный уровень добычи нефти или газа; б) минимум затрат; в) возможно более полное извлечение нефти или газа. Такая система является рациональной. Установление рациональной системы разработки путем промыслового эксперимента невозможно.
 3 С этой целью используют гидродинамические расчеты и модели-рование, то есть рассчитывают показатели разработки с помощью тех или иных теоретических зависимостей. Сущность гидродинамических методов заключается в установ-лении количественной связи между поведением дебитов сква-жин и давлений на забоях этих скважин и на определенных контурах, скоростей и сроков перемещения отдельных частиц пластовой жидкости в зависимости от формы залежи, параметров пласта, физико-химических свойств нефти, воды, газа и их смесей, числа и взаимного расположения скважин. Расчетные формулы базируются на: − основных законах фильтрации жидкостей в пористых и трещиновато- пористых средах; − законах взаимодействия отдельных скважин в процессе их совместной работы.
3 С этой целью используют гидродинамические расчеты и модели-рование, то есть рассчитывают показатели разработки с помощью тех или иных теоретических зависимостей. Сущность гидродинамических методов заключается в установ-лении количественной связи между поведением дебитов сква-жин и давлений на забоях этих скважин и на определенных контурах, скоростей и сроков перемещения отдельных частиц пластовой жидкости в зависимости от формы залежи, параметров пласта, физико-химических свойств нефти, воды, газа и их смесей, числа и взаимного расположения скважин. Расчетные формулы базируются на: − основных законах фильтрации жидкостей в пористых и трещиновато- пористых средах; − законах взаимодействия отдельных скважин в процессе их совместной работы.
 4 Для получения надежных результатов проектирования требуется предварительно создать модель разработки. Модель разработки можно определить как систему взаимосвя-занных количественных представлений о разработке залежи, которая состоит из модели пласта и модели процесса извлечения. Обе модели всегда облечены в математическую форму, т. е. харак-теризуются определенными математическими соотношениями. Как любая другая математическая модель, они основаны на упрощении (идеализации) реального состояния или процесса, что позволяет создать расчетные схемы, учитывающие только основные эффекты.
4 Для получения надежных результатов проектирования требуется предварительно создать модель разработки. Модель разработки можно определить как систему взаимосвя-занных количественных представлений о разработке залежи, которая состоит из модели пласта и модели процесса извлечения. Обе модели всегда облечены в математическую форму, т. е. харак-теризуются определенными математическими соотношениями. Как любая другая математическая модель, они основаны на упрощении (идеализации) реального состояния или процесса, что позволяет создать расчетные схемы, учитывающие только основные эффекты.
 5 Основными задачами подземной гидромеханики являются : 1) создание теории и методов расчета движения реальных жидкостей (газов) в пористых средах в процессе извлечения нефти или газа из недр; 2) получение данных, необходимых для научно обоснованного проектирования разработки месторождений углеводородного сырья.
5 Основными задачами подземной гидромеханики являются : 1) создание теории и методов расчета движения реальных жидкостей (газов) в пористых средах в процессе извлечения нефти или газа из недр; 2) получение данных, необходимых для научно обоснованного проектирования разработки месторождений углеводородного сырья.
 6 Этапы развития подземной гидромеханики Начало развитию подземной гидромеханики было положено французским инженером А. Дарси, который в процессе работы над проектом водоснабжения г. Дижона провел многочисленные опыты по изучению фильтрации воды через вертикальные песчаные фильтры. В 1856 г. им была опубликована книга с описанием опытов. В ней же был сформулирован экспериментальный закон, в соответ-ствии с которым скорость фильтрации жидкости прямо пропор-циональна градиенту давления. В эти же годы другой французский инженер Дюпюи опубли-ковал монографию, в которой впервые изложил гидравлическую теорию движения грунтовых вод.
6 Этапы развития подземной гидромеханики Начало развитию подземной гидромеханики было положено французским инженером А. Дарси, который в процессе работы над проектом водоснабжения г. Дижона провел многочисленные опыты по изучению фильтрации воды через вертикальные песчаные фильтры. В 1856 г. им была опубликована книга с описанием опытов. В ней же был сформулирован экспериментальный закон, в соответ-ствии с которым скорость фильтрации жидкости прямо пропор-циональна градиенту давления. В эти же годы другой французский инженер Дюпюи опубли-ковал монографию, в которой впервые изложил гидравлическую теорию движения грунтовых вод.
 7 Ч. Слихтер — гидрогеолог, работавший в США, — внес значительный вклад в развитие теории фильтрации. Им впервые были пред-ложены модели идеального и фиктивного грунтов, показано, что пористость и просветность фиктивного грунта зависят не от диаметра частиц, а лишь от плотности их укладки. Основоположниками отечественной школы теории фильтрации являются проф. Н. Е. Жуковский, академики Н. Н. Павловский и Л. С. Лейбензон. Н. Е. Жуковский в 1889 г. опубликовал первую работу по теории фильтрации “Теоретическое исследование о движении подпочвен-ных вод”. Им впервые были выведены общие ифференциальные уравнения теории фильтрации, указано на математическую аналогию теплопроводности и фильтрации. Им также решен ряд задач о притоке воды к скважинам.
7 Ч. Слихтер — гидрогеолог, работавший в США, — внес значительный вклад в развитие теории фильтрации. Им впервые были пред-ложены модели идеального и фиктивного грунтов, показано, что пористость и просветность фиктивного грунта зависят не от диаметра частиц, а лишь от плотности их укладки. Основоположниками отечественной школы теории фильтрации являются проф. Н. Е. Жуковский, академики Н. Н. Павловский и Л. С. Лейбензон. Н. Е. Жуковский в 1889 г. опубликовал первую работу по теории фильтрации “Теоретическое исследование о движении подпочвен-ных вод”. Им впервые были выведены общие ифференциальные уравнения теории фильтрации, указано на математическую аналогию теплопроводности и фильтрации. Им также решен ряд задач о притоке воды к скважинам.
 8 Н. Н. Павловским многие задачи фильтрации воды были сформули-рованы как краевые задачи математической физики. Он же впервые обосновал и предложил применение метода электро-динамической аналогии (ЭГДА) для решения фильтрационных задач, что в последующем нашло широкое применение для решения задач фильтрации нефти, воды и газа в продуктивных пластах. Н. Н. Павловский впервые предложил использовать пара-метр Рейнольдса в качестве критерия существования закона Дарси. Вплоть до середины 20 -х годов ХХ века подземная гидромеханика развивалась преимущественно в рамках инженерной гидро-геологии (отсюда название). В 20 -х и начале 30 -х годов этого века прогнозирование разработки нефтяных месторождений производилось в основном путем построения фактических зависимостей показателей разработки от времени, полученных в начальный период разработки, статистической обработки этих показателей и их экстраполяции на будущее.
8 Н. Н. Павловским многие задачи фильтрации воды были сформули-рованы как краевые задачи математической физики. Он же впервые обосновал и предложил применение метода электро-динамической аналогии (ЭГДА) для решения фильтрационных задач, что в последующем нашло широкое применение для решения задач фильтрации нефти, воды и газа в продуктивных пластах. Н. Н. Павловский впервые предложил использовать пара-метр Рейнольдса в качестве критерия существования закона Дарси. Вплоть до середины 20 -х годов ХХ века подземная гидромеханика развивалась преимущественно в рамках инженерной гидро-геологии (отсюда название). В 20 -х и начале 30 -х годов этого века прогнозирование разработки нефтяных месторождений производилось в основном путем построения фактических зависимостей показателей разработки от времени, полученных в начальный период разработки, статистической обработки этих показателей и их экстраполяции на будущее.
 9 Математические методы теории фильтрации, уже значительно развитые к этому времени Н. Е. Жуковским, Н. Н. Павловским и другими, еще не нашли применения в нефтяном деле. Основателем отечественной школы ученых и специалистов в области гидродинамической теории фильтрации нефти и газа является академик Л. С. Лейбензон. Теоретические и эспери-ментальные исследования Л. С. Лейбензона начались в 1921 г. в Баку. Обобщение этих исследований приведено в монографии “Нефтепромысловая механика”, в которой впервые изложены основы нефтегазовой подземной гидромеханики (1934 г. ). Выдающийся вклад в развитие теории фильтрации в нефте-газоводоносных пластах внесли С. А. Христианович, Б. Б. Лапук, И. А. Чарный, В. Н. Щелкачев и другие ученые.
9 Математические методы теории фильтрации, уже значительно развитые к этому времени Н. Е. Жуковским, Н. Н. Павловским и другими, еще не нашли применения в нефтяном деле. Основателем отечественной школы ученых и специалистов в области гидродинамической теории фильтрации нефти и газа является академик Л. С. Лейбензон. Теоретические и эспери-ментальные исследования Л. С. Лейбензона начались в 1921 г. в Баку. Обобщение этих исследований приведено в монографии “Нефтепромысловая механика”, в которой впервые изложены основы нефтегазовой подземной гидромеханики (1934 г. ). Выдающийся вклад в развитие теории фильтрации в нефте-газоводоносных пластах внесли С. А. Христианович, Б. Б. Лапук, И. А. Чарный, В. Н. Щелкачев и другие ученые.
 10 Широкие исследования в области подземной гидромеханики ведутся за рубежом. Стали классическими экспериментальные исследования, проведенные в США еще в 30 -е годы ХХ века Р. Викофом и Г. Ботсетом по изучению фазовых проницаемостей жидкости и газа. Существенное значение имеет классическая теория двухфазной фильтрации, предложенная С. Бакли и М. Левереттом. Значительное влияние на развитие теории фильтрации оказала работа А. Ван- Эвердингена и У. Херста о притоке упругой жидкости к скважине.
10 Широкие исследования в области подземной гидромеханики ведутся за рубежом. Стали классическими экспериментальные исследования, проведенные в США еще в 30 -е годы ХХ века Р. Викофом и Г. Ботсетом по изучению фазовых проницаемостей жидкости и газа. Существенное значение имеет классическая теория двухфазной фильтрации, предложенная С. Бакли и М. Левереттом. Значительное влияние на развитие теории фильтрации оказала работа А. Ван- Эвердингена и У. Херста о притоке упругой жидкости к скважине.
 11 В настоящее время интенсивно развиваются : − теория многофазной многокомпонентной фильтрации флюидов в деформируемых неоднородных пластах; − физико-химическая гидродинамика и гидродинамика новых методов извлечения нефти и газа из недр; − теория фильтрации неньютоновских жидкостей и неуглеводо-родных дисперсных систем; − подземная гидротермодинамика; − теория нелинейной нестационарной фильтрации и др. Для решения современных гидродинамических задач применяют широко развитый аппарат математической физики, вероят-ностно-статистические методы, используют возможности вычислительной техники.
11 В настоящее время интенсивно развиваются : − теория многофазной многокомпонентной фильтрации флюидов в деформируемых неоднородных пластах; − физико-химическая гидродинамика и гидродинамика новых методов извлечения нефти и газа из недр; − теория фильтрации неньютоновских жидкостей и неуглеводо-родных дисперсных систем; − подземная гидротермодинамика; − теория нелинейной нестационарной фильтрации и др. Для решения современных гидродинамических задач применяют широко развитый аппарат математической физики, вероят-ностно-статистические методы, используют возможности вычислительной техники.
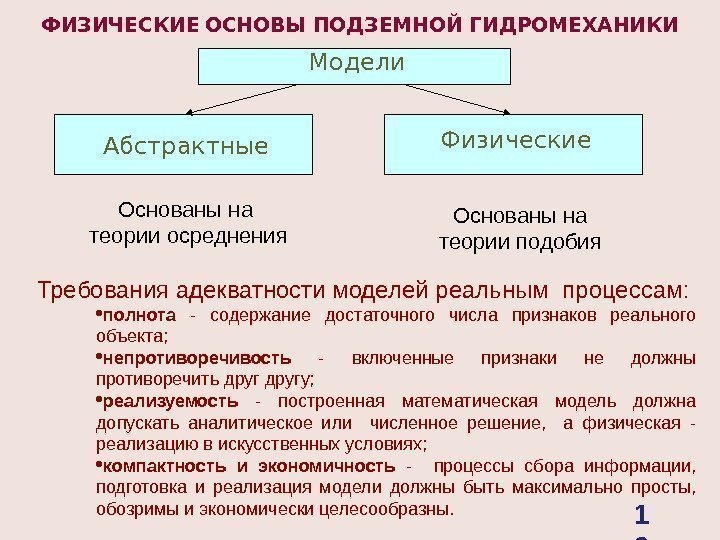
 ФИЗИЧЕСКИЕ ОСНОВЫ ПОДЗЕМНОЙ ГИДРОМЕХАНИКИ Модели Абстрактные Физические Требования адекватности моделей реальным процессам: полнота — содержание достаточного числа признаков реального объекта; непротиворечивость — включенные признаки не должны противоречить другу; реализуемость — построенная математическая модель должна допускать аналитическое или численное решение, а физическая — реализацию в искусственных условиях; компактность и экономичность — процессы сбора информации, подготовка и реализация модели должны быть максимально просты, обозримы и экономически целесообразны. Основаны на теории осреднения Основаны на теории подобия
ФИЗИЧЕСКИЕ ОСНОВЫ ПОДЗЕМНОЙ ГИДРОМЕХАНИКИ Модели Абстрактные Физические Требования адекватности моделей реальным процессам: полнота — содержание достаточного числа признаков реального объекта; непротиворечивость — включенные признаки не должны противоречить другу; реализуемость — построенная математическая модель должна допускать аналитическое или численное решение, а физическая — реализацию в искусственных условиях; компактность и экономичность — процессы сбора информации, подготовка и реализация модели должны быть максимально просты, обозримы и экономически целесообразны. Основаны на теории осреднения Основаны на теории подобия
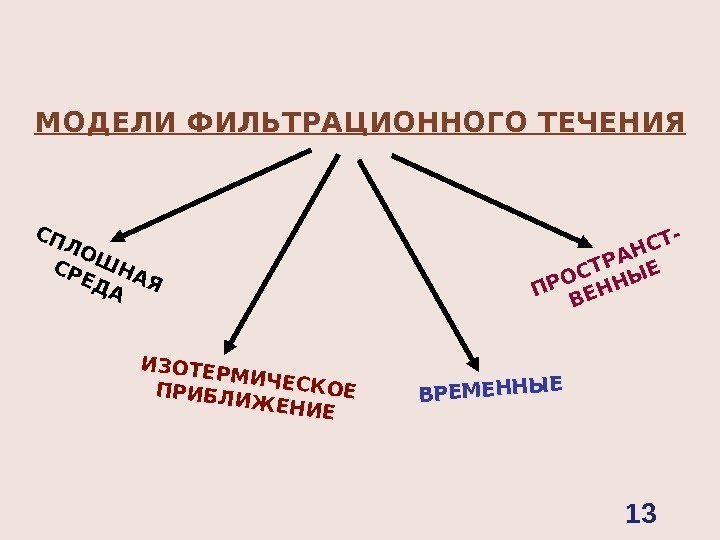
 МОДЕЛИ ФИЛЬТРАЦИОННОГО ТЕЧЕНИЯСПЛОШНАЯ СРЕДА ИЗОТЕРМИЧЕСКОЕ ПРИБЛИЖЕНИЕ ВРЕМЕННЫЕ ПРОСТРАНСТ- ВЕННЫЕ
МОДЕЛИ ФИЛЬТРАЦИОННОГО ТЕЧЕНИЯСПЛОШНАЯ СРЕДА ИЗОТЕРМИЧЕСКОЕ ПРИБЛИЖЕНИЕ ВРЕМЕННЫЕ ПРОСТРАНСТ- ВЕННЫЕ
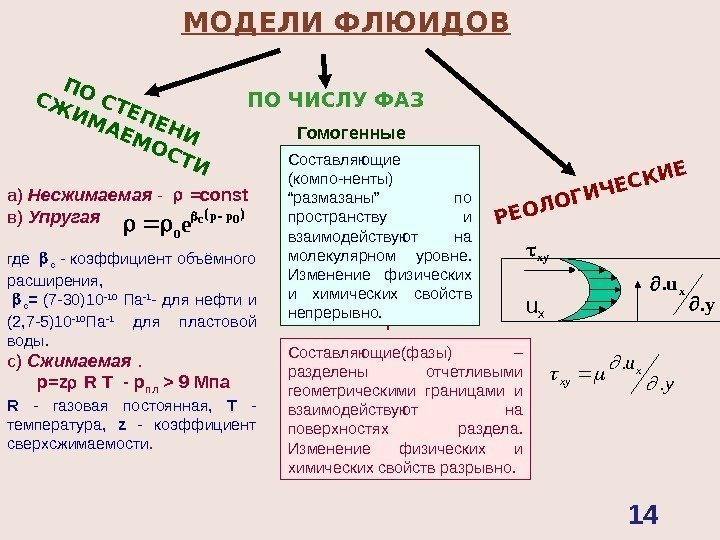
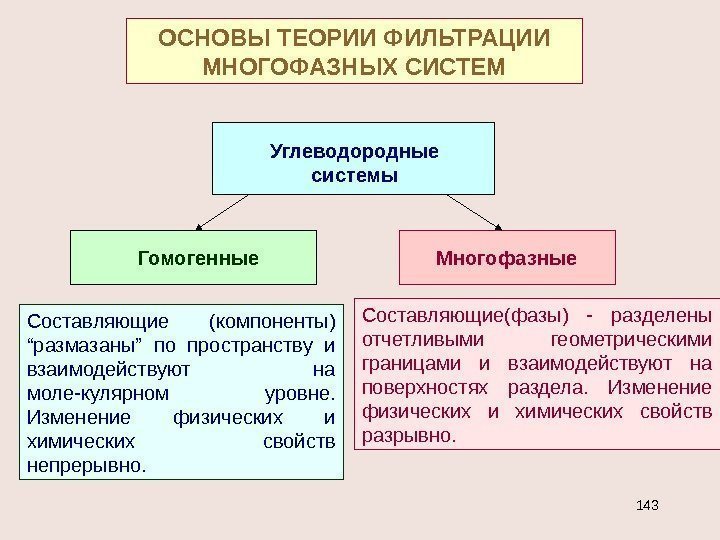
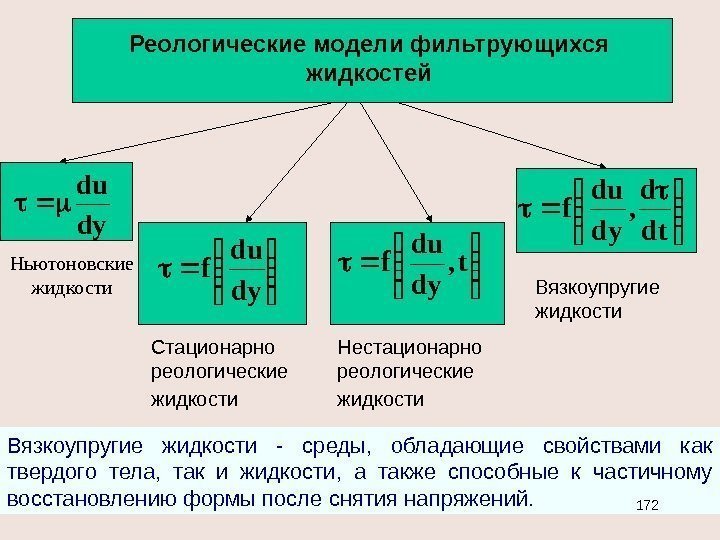
 ПО СТЕПЕНИ СЖИМАЕМОСТИПО ЧИСЛУ ФАЗ РЕОЛОГИЧЕСКИЕМОДЕЛИ ФЛЮИДОВ yu x xy. . а) Несжимаемая — =со nst в) Упругая где c — коэффициент объёмного расширения, c = (7 -30)10 -10 Па -1 — для нефти и (2, 7 -5)10 -10 Па -1 для пластовой воды. с) Сжимаемая . р =z R T — р пл > 9 Мпа R — газовая постоянная, Т — температура, z — коэффициент сверхсжимаемости. 0 ррс 0 e Гомогенные Многофазные. Составляющие (компо — ненты) “размазаны” по пространству и взаимодействуют на молекулярном уровне. Изменение физических и химических свойств непрерывно. u x y. u. x xy Составляющие(фазы) – разделены отчетливыми геометрическими границами и взаимодействуют на поверхностях раздела. Изменение физических и химических свойств разрывно.
ПО СТЕПЕНИ СЖИМАЕМОСТИПО ЧИСЛУ ФАЗ РЕОЛОГИЧЕСКИЕМОДЕЛИ ФЛЮИДОВ yu x xy. . а) Несжимаемая — =со nst в) Упругая где c — коэффициент объёмного расширения, c = (7 -30)10 -10 Па -1 — для нефти и (2, 7 -5)10 -10 Па -1 для пластовой воды. с) Сжимаемая . р =z R T — р пл > 9 Мпа R — газовая постоянная, Т — температура, z — коэффициент сверхсжимаемости. 0 ррс 0 e Гомогенные Многофазные. Составляющие (компо — ненты) “размазаны” по пространству и взаимодействуют на молекулярном уровне. Изменение физических и химических свойств непрерывно. u x y. u. x xy Составляющие(фазы) – разделены отчетливыми геометрическими границами и взаимодействуют на поверхностях раздела. Изменение физических и химических свойств разрывно.
 МОДЕЛИ КОЛЛЕКТОРОВ
МОДЕЛИ КОЛЛЕКТОРОВ
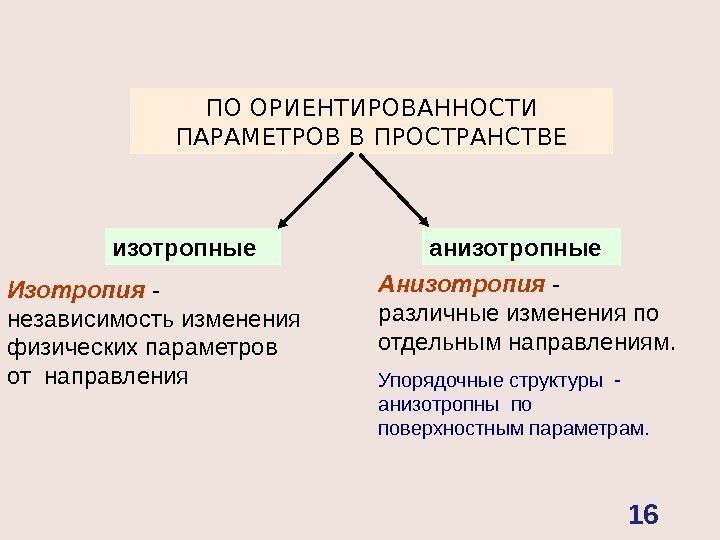
 ПО ОРИЕНТИРОВАННОСТИ ПАРАМЕТРОВ В ПРОСТРАНСТВЕ изотропные анизотропные Изотропия — независимость изменения физических параметров от направления Анизотропия — различные изменения по отдельным направлениям. Упорядочные структуры — анизотропны по поверхностным параметрам.
ПО ОРИЕНТИРОВАННОСТИ ПАРАМЕТРОВ В ПРОСТРАНСТВЕ изотропные анизотропные Изотропия — независимость изменения физических параметров от направления Анизотропия — различные изменения по отдельным направлениям. Упорядочные структуры — анизотропны по поверхностным параметрам.
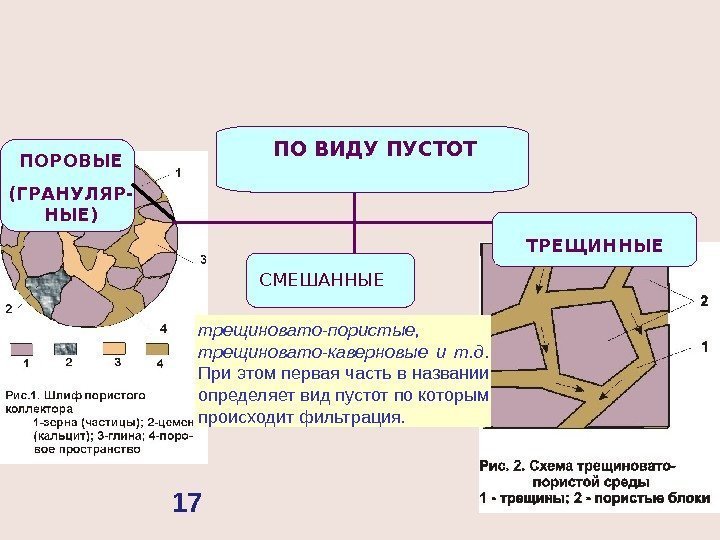
 СМЕШАННЫЕ ТРЕЩИННЫЕПО ВИДУ ПУСТОТ ПОРОВЫЕ (ГРАНУЛЯР- НЫЕ) трещиновато-пористые, трещиновато-каверновые и т. д. При этом первая часть в названии определяет вид пустот по которым происходит фильтрация.
СМЕШАННЫЕ ТРЕЩИННЫЕПО ВИДУ ПУСТОТ ПОРОВЫЕ (ГРАНУЛЯР- НЫЕ) трещиновато-пористые, трещиновато-каверновые и т. д. При этом первая часть в названии определяет вид пустот по которым происходит фильтрация.
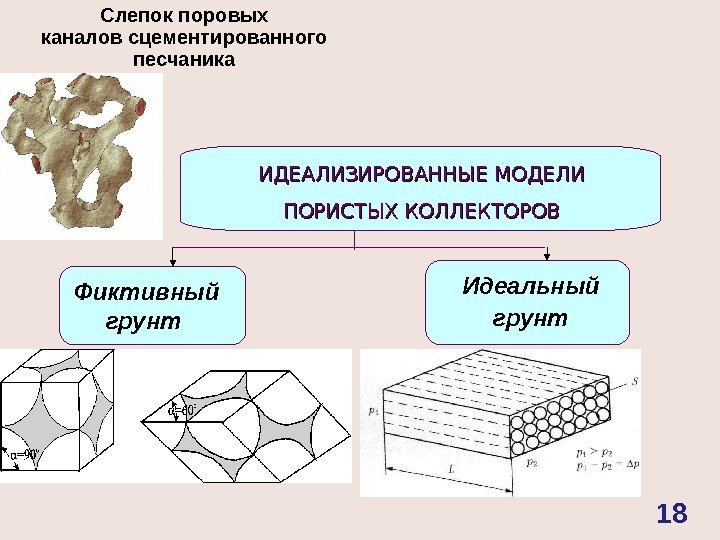
 Фиктивный грунт Идеальный грунт ИДЕАЛИЗИРОВАННЫЕ МОДЕЛИ ПОРИСТЫХ КОЛЛЕКТОРОВ Слепок поровых каналов сцементированного песчаника
Фиктивный грунт Идеальный грунт ИДЕАЛИЗИРОВАННЫЕ МОДЕЛИ ПОРИСТЫХ КОЛЛЕКТОРОВ Слепок поровых каналов сцементированного песчаника
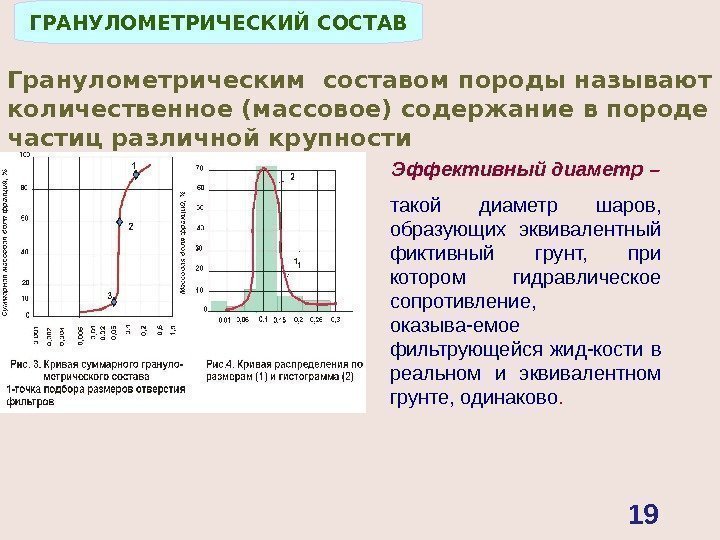
 ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВ Гранулометрическим составом породы называют количественное (массовое) содержание в породе частиц различной крупности Эффективный диаметр – такой диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлическое сопротивление, оказыва — емое фильтрующейся жид — кости в реальном и эквивалентном грунте, одинаково.
ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВ Гранулометрическим составом породы называют количественное (массовое) содержание в породе частиц различной крупности Эффективный диаметр – такой диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлическое сопротивление, оказыва — емое фильтрующейся жид — кости в реальном и эквивалентном грунте, одинаково.
 ФИЛЬТРАЦИОННО — ЁМКОСТНЫЕ ПАРАМЕТРЫ ПОРИСТЫХ КОЛЛЕКТОРОВ ЁМКОСТНЫЕ ПОРИСТОСТЬ ФИЛЬТРАЦИОННЫЕ ПРОНИЦАЕМОСТЬ
ФИЛЬТРАЦИОННО — ЁМКОСТНЫЕ ПАРАМЕТРЫ ПОРИСТЫХ КОЛЛЕКТОРОВ ЁМКОСТНЫЕ ПОРИСТОСТЬ ФИЛЬТРАЦИОННЫЕ ПРОНИЦАЕМОСТЬ
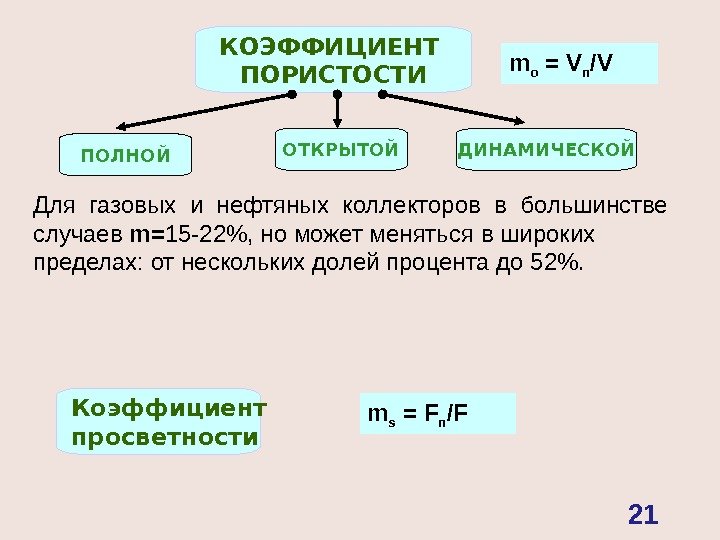
 КОЭФФИЦИЕНТ ПОРИСТОСТИ m о = V п /V ПОЛНОЙ ДИНАМИЧЕСКОЙОТКРЫТОЙ Коэффициент просветности m s = F п / F Для газовых и нефтяных коллекторов в большинстве случаев m= 15 -22%, но может меняться в широких пределах: от нескольких долей процента до 52%.
КОЭФФИЦИЕНТ ПОРИСТОСТИ m о = V п /V ПОЛНОЙ ДИНАМИЧЕСКОЙОТКРЫТОЙ Коэффициент просветности m s = F п / F Для газовых и нефтяных коллекторов в большинстве случаев m= 15 -22%, но может меняться в широких пределах: от нескольких долей процента до 52%.
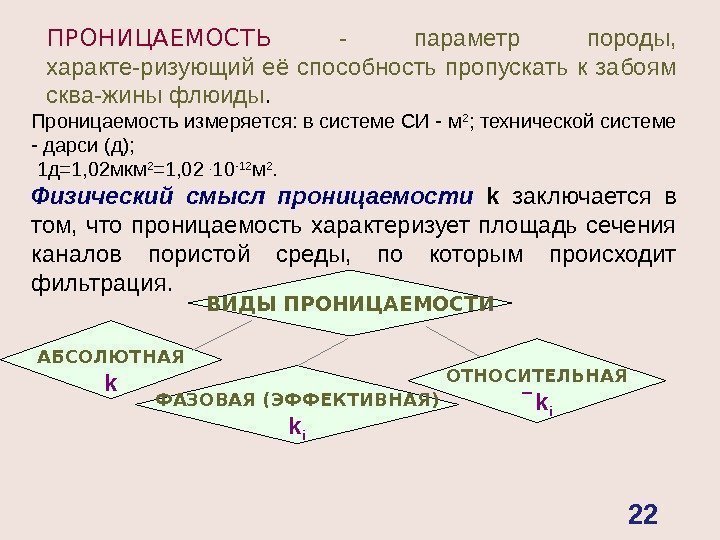
 ПРОНИЦАЕМОСТЬ — параметр породы, характе-ризующий её способность пропускать к забоям сква-жины флюиды. Проницаемость измеряется: в системе СИ — м 2 ; технической системе — дарси (д); 1 д=1, 02 мкм 2 =1, 02 . 10 -12 м 2. Физический смысл проницаемости k заключается в том, что проницаемость характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация. ВИДЫ ПРОНИЦАЕМОСТИ АБСОЛЮТНАЯ k ФАЗОВАЯ (ЭФФЕКТИВНАЯ) k i ОТНОСИТЕЛЬНАЯ k i
ПРОНИЦАЕМОСТЬ — параметр породы, характе-ризующий её способность пропускать к забоям сква-жины флюиды. Проницаемость измеряется: в системе СИ — м 2 ; технической системе — дарси (д); 1 д=1, 02 мкм 2 =1, 02 . 10 -12 м 2. Физический смысл проницаемости k заключается в том, что проницаемость характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация. ВИДЫ ПРОНИЦАЕМОСТИ АБСОЛЮТНАЯ k ФАЗОВАЯ (ЭФФЕКТИВНАЯ) k i ОТНОСИТЕЛЬНАЯ k i
 а) коэффициент насыщенности — отношение объёма Vf данного флюида, содержащегося в порах, к объёму пор Vп По виду флюида различают нефтенасыщенность, газонасыщенность, водонасыщенность. б) коэффициент связанности — отношение объёма, связанного с породой флюида V f с , к объёму пор ПАРАМЕТРЫ, СВЯЗАННЫЕ С НАЛИЧИЕМ ФЛЮИДОВп f f V V п fc f V V c
а) коэффициент насыщенности — отношение объёма Vf данного флюида, содержащегося в порах, к объёму пор Vп По виду флюида различают нефтенасыщенность, газонасыщенность, водонасыщенность. б) коэффициент связанности — отношение объёма, связанного с породой флюида V f с , к объёму пор ПАРАМЕТРЫ, СВЯЗАННЫЕ С НАЛИЧИЕМ ФЛЮИДОВп f f V V п fc f V V c
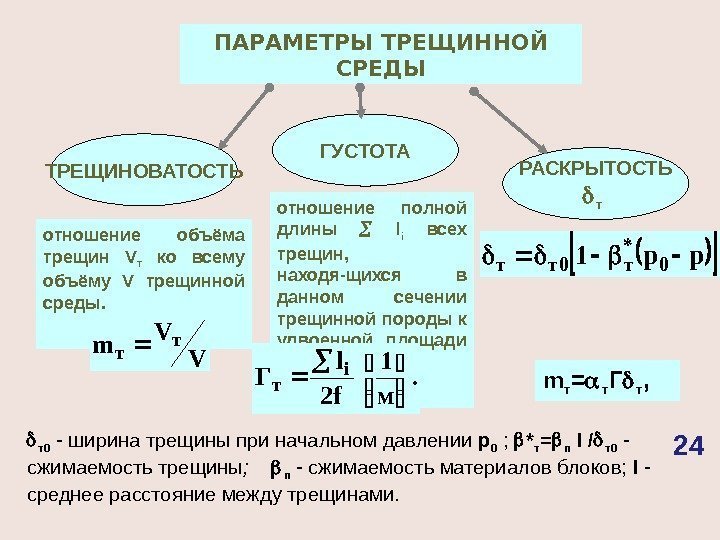
 ПАРАМЕТРЫ ТРЕЩИННОЙ СРЕДЫ ТРЕЩИНОВАТОСТЬ ГУСТОТА РАСКРЫТОСТЬ т отношение объёма трещин V т ко всему объёму V трещинной среды. V V mт т отношение полной длины l i всех трещин, находя-щихся в данном сечении трещинной породы к удвоенной площади сечения f. м 1 f 2 l Г i т m т = т Г т , рр10 * т0 тт т0 — ширина трещины при начальном давлении р 0 ; * т = п l / т0 — сжимаемость трещины ; п — сжимаемость материалов блоков; l — среднее расстояние между трещинами.
ПАРАМЕТРЫ ТРЕЩИННОЙ СРЕДЫ ТРЕЩИНОВАТОСТЬ ГУСТОТА РАСКРЫТОСТЬ т отношение объёма трещин V т ко всему объёму V трещинной среды. V V mт т отношение полной длины l i всех трещин, находя-щихся в данном сечении трещинной породы к удвоенной площади сечения f. м 1 f 2 l Г i т m т = т Г т , рр10 * т0 тт т0 — ширина трещины при начальном давлении р 0 ; * т = п l / т0 — сжимаемость трещины ; п — сжимаемость материалов блоков; l — среднее расстояние между трещинами.
 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ФИЛЬТРАЦИИ при отсутствии источников — стоков
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ФИЛЬТРАЦИИ при отсутствии источников — стоков
 Математическое описание гидродинамических процессов Смысл дифференциального уравнения Каждое из дифференциальных уравнений гидродинамики выражает определенный закон сохранения, в котором в качестве зависимой переменной используется некоторая физическая величина и отражен баланс между различными факторами, влияющими на эту переменную. Зависимыми переменными являются удельные свойства, т. е. свойства, отнесенные к единице массы, примерами являются: массовая концентрация, скорость (т. е. количество движения единицы массы), удельная энергия. Ч истое истечение на единицу объемаdiv. J z J y J x J zy x t Ф — скорость изменения соответствующего свойства в единице объема. Дифференциальное уравнение состоит из членов, каждый из которых выражает воздействие на единицу объема, а сумма — баланс этих воздействий.
Математическое описание гидродинамических процессов Смысл дифференциального уравнения Каждое из дифференциальных уравнений гидродинамики выражает определенный закон сохранения, в котором в качестве зависимой переменной используется некоторая физическая величина и отражен баланс между различными факторами, влияющими на эту переменную. Зависимыми переменными являются удельные свойства, т. е. свойства, отнесенные к единице массы, примерами являются: массовая концентрация, скорость (т. е. количество движения единицы массы), удельная энергия. Ч истое истечение на единицу объемаdiv. J z J y J x J zy x t Ф — скорость изменения соответствующего свойства в единице объема. Дифференциальное уравнение состоит из членов, каждый из которых выражает воздействие на единицу объема, а сумма — баланс этих воздействий.
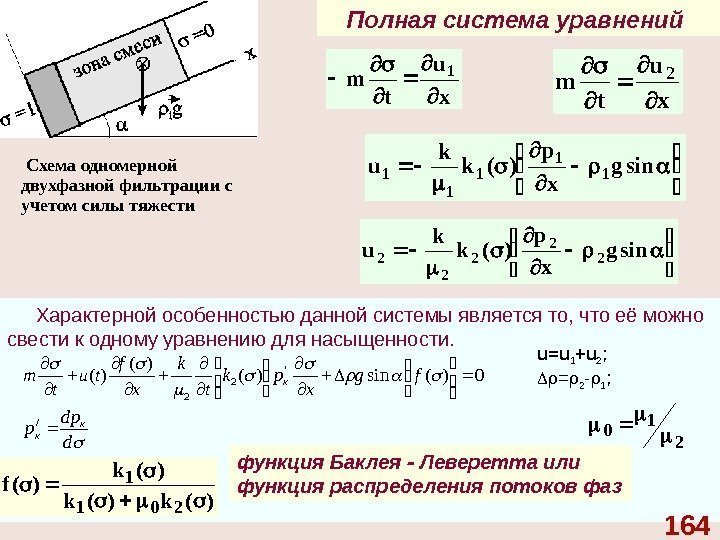
 1. Уравнение неразрывности 0 udiv t m 2. Уравнение движения где р * =р+ z g , u = d. G / dt , G — расход массы жидкости в единицу времени через поверхность равного потенциала (массовый дебит); среда изотропна ( k = const , μ = const ) c *2 Fgradpmudiv t u = 0 – течение медленное = 0 – изменение кинетической энергии мало u сau Re c 12 — массовая сила сопротивления флюида о скелет горной породы Получаем уравнение движения в форме Дарси * gradp k u
1. Уравнение неразрывности 0 udiv t m 2. Уравнение движения где р * =р+ z g , u = d. G / dt , G — расход массы жидкости в единицу времени через поверхность равного потенциала (массовый дебит); среда изотропна ( k = const , μ = const ) c *2 Fgradpmudiv t u = 0 – течение медленное = 0 – изменение кинетической энергии мало u сau Re c 12 — массовая сила сопротивления флюида о скелет горной породы Получаем уравнение движения в форме Дарси * gradp k u
 Уравнение неразрывности при установившаяся фильтрации : • сжимаемой жидкости • несжимаемой жидкостиz f y f x f fdivzyx k z +j y +i x grad равна сумме производных проекций векторной функции по соответствующим координатам 0 udiv 28 равен сумме произведений производных скалярной функции по координатам на единичные вектора данных координат
Уравнение неразрывности при установившаяся фильтрации : • сжимаемой жидкости • несжимаемой жидкостиz f y f x f fdivzyx k z +j y +i x grad равна сумме производных проекций векторной функции по соответствующим координатам 0 udiv 28 равен сумме произведений производных скалярной функции по координатам на единичные вектора данных координат
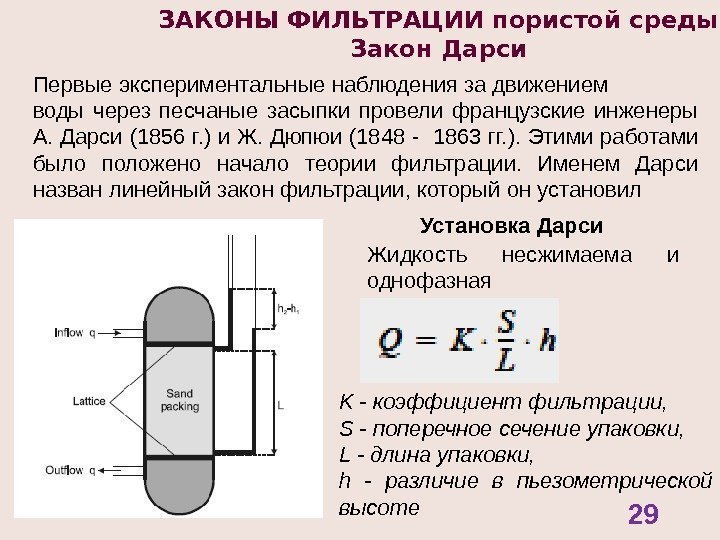
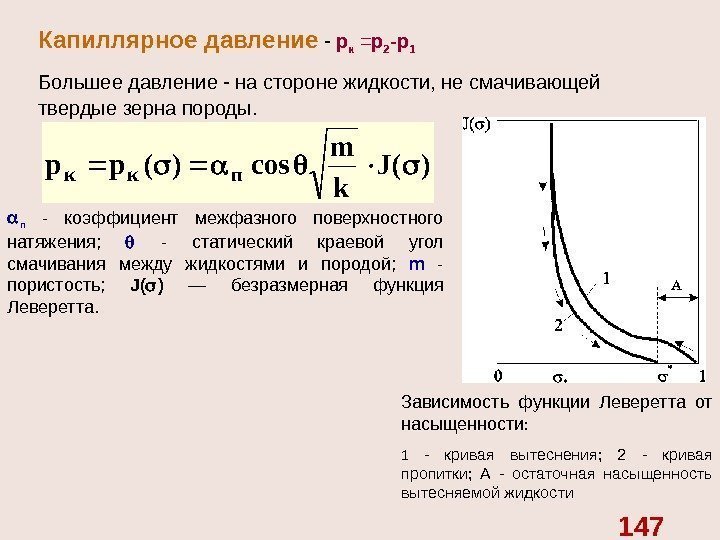
 Первые экспериментальные наблюдения за движением воды через песчаные засыпки провели французские инженеры А. Дарси (1856 г. ) и Ж. Дюпюи (1848 — 1863 гг. ). Этими работами было положено начало теории фильтрации. Именем Дарси назван линейный закон фильтрации, который он установил ЗАКОНЫ ФИЛЬТРАЦИИ пористой среды Закон Дарси Установка Дарси Жидкость несжимаема и однофазная K — коэффициент фильтрации, S — поперечное сечение упаковки, L — длина упаковки, h — различие в пьезометрической высоте
Первые экспериментальные наблюдения за движением воды через песчаные засыпки провели французские инженеры А. Дарси (1856 г. ) и Ж. Дюпюи (1848 — 1863 гг. ). Этими работами было положено начало теории фильтрации. Именем Дарси назван линейный закон фильтрации, который он установил ЗАКОНЫ ФИЛЬТРАЦИИ пористой среды Закон Дарси Установка Дарси Жидкость несжимаема и однофазная K — коэффициент фильтрации, S — поперечное сечение упаковки, L — длина упаковки, h — различие в пьезометрической высоте
 На первом Мировом Нефтяном Конгрессе в 1933 г. Fancher, Lewis и Barnes ввели понятие проницаемости. В том же самом году Wyckoff, Botset, Muskat и Reed предложили единицу проницаемости назвать именем Дарси. С того времени Закон Дарси описывается уравнением где: A — поперечное сечение пористой среды k – абсолютная проницаемость L — длина пористой среды Δp — перепад давления на пористой среде μ – вязкость жидкости
На первом Мировом Нефтяном Конгрессе в 1933 г. Fancher, Lewis и Barnes ввели понятие проницаемости. В том же самом году Wyckoff, Botset, Muskat и Reed предложили единицу проницаемости назвать именем Дарси. С того времени Закон Дарси описывается уравнением где: A — поперечное сечение пористой среды k – абсолютная проницаемость L — длина пористой среды Δp — перепад давления на пористой среде μ – вязкость жидкости
 Дарси ( Darcy ) — единица измерения проницаемости горных пород, выражающая их способность фильтровать жидкость с динамической вязкостью 1 спз через площадь поперечного сечения 1 см² со скоростью 1 см/сек при градиенте давления жидкости по направлению фильтрации 1 атм/ см
Дарси ( Darcy ) — единица измерения проницаемости горных пород, выражающая их способность фильтровать жидкость с динамической вязкостью 1 спз через площадь поперечного сечения 1 см² со скоростью 1 см/сек при градиенте давления жидкости по направлению фильтрации 1 атм/ см
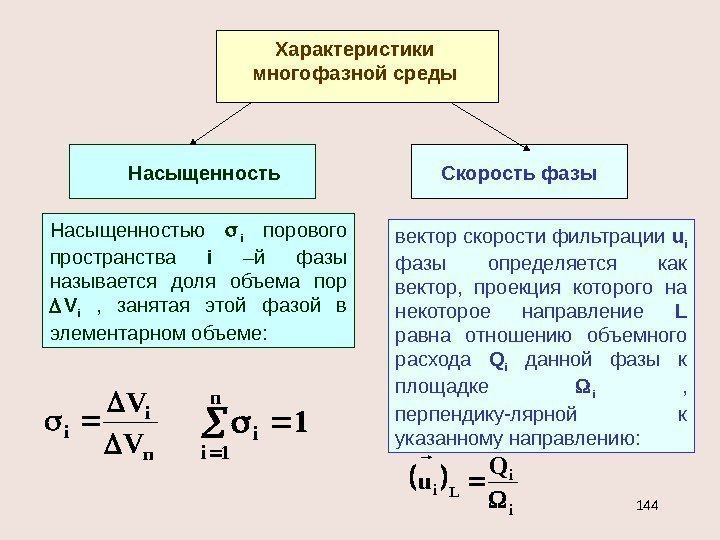
 СКОРОСТЬ ФИЛЬТРАЦИИ: Q = w F п = w m F mwu Физический смысл скорости фильтрации — среднерасходная скорость фиктивного потока, в котором расход через любое сечение равен реальному расходу, поля давлений фиктивного и реального потоков идентичны, а сила сопротивления фиктивного потока равна реальной.
СКОРОСТЬ ФИЛЬТРАЦИИ: Q = w F п = w m F mwu Физический смысл скорости фильтрации — среднерасходная скорость фиктивного потока, в котором расход через любое сечение равен реальному расходу, поля давлений фиктивного и реального потоков идентичны, а сила сопротивления фиктивного потока равна реальной.
 )( ln 2 ск c к рр r r hk Q Уравнение притока в форме Дюпюи * gradp k u Уравнение Дарси в дифференциальной форме к 2 к ст ст r р pz hk Q ln нефть газ z = ( z c + z к ) / 2; μ = ( μ c + μ к ) / 2; z с = z ( p с ), μ с = μ ( p с ), z к = z ( p к ), μ к = μ ( p к ). р* = р + pgz — приведенное давление
)( ln 2 ск c к рр r r hk Q Уравнение притока в форме Дюпюи * gradp k u Уравнение Дарси в дифференциальной форме к 2 к ст ст r р pz hk Q ln нефть газ z = ( z c + z к ) / 2; μ = ( μ c + μ к ) / 2; z с = z ( p с ), μ с = μ ( p с ), z к = z ( p к ), μ к = μ ( p к ). р* = р + pgz — приведенное давление
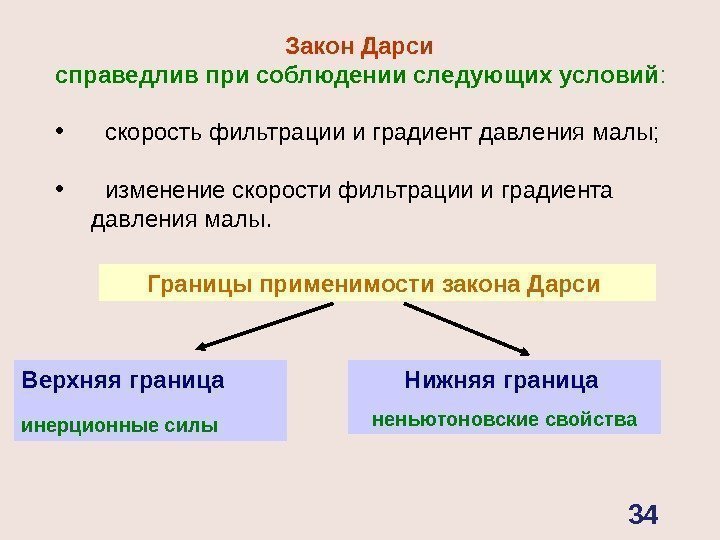
 Границы применимости закона Дарси Верхняя граница инерционные силы Нижняя граница неньютоновские свойства. Закон Дарси справедлив при соблюдении следующих условий : • скорость фильтрации и градиент давления малы; • изменение скорости фильтрации и градиента давления малы.
Границы применимости закона Дарси Верхняя граница инерционные силы Нижняя граница неньютоновские свойства. Закон Дарси справедлив при соблюдении следующих условий : • скорость фильтрации и градиент давления малы; • изменение скорости фильтрации и градиента давления малы.
 Число Рейнольдса Re = wa / μ ; w -характерная скорость течения: а — характерный геометри-ческий размер пористой среды; — плотность жидкости Зависимость Павловского Критическое число Рейнольдса Re кр =7, 5 -9. Зависимость Щелкачёва: Критическое число Рейнольдса Re кр =1 -12. Скорость фильтрации u кр , при которой нарушается закон Дарси, называется критической скоростью фильтрации Верхняя граница. = где , w=u; m k 10 а m ku 10 Re 3, 2 . ; 23, 075, 0 где , 23, 075, 0 Re w=u m dа= m ud
Число Рейнольдса Re = wa / μ ; w -характерная скорость течения: а — характерный геометри-ческий размер пористой среды; — плотность жидкости Зависимость Павловского Критическое число Рейнольдса Re кр =7, 5 -9. Зависимость Щелкачёва: Критическое число Рейнольдса Re кр =1 -12. Скорость фильтрации u кр , при которой нарушается закон Дарси, называется критической скоростью фильтрации Верхняя граница. = где , w=u; m k 10 а m ku 10 Re 3, 2 . ; 23, 075, 0 где , 23, 075, 0 Re w=u m dа= m ud
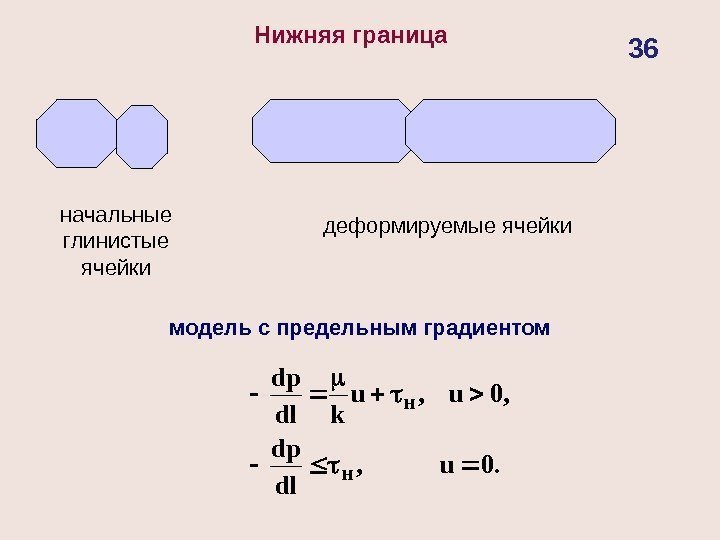
 Нижняя граница. 0 u, dl dp , 0 u, u kdl dp н н модель с предельным градиентомначальные глинистые ячейки деформируемые ячейки
Нижняя граница. 0 u, dl dp , 0 u, u kdl dp н н модель с предельным градиентомначальные глинистые ячейки деформируемые ячейки
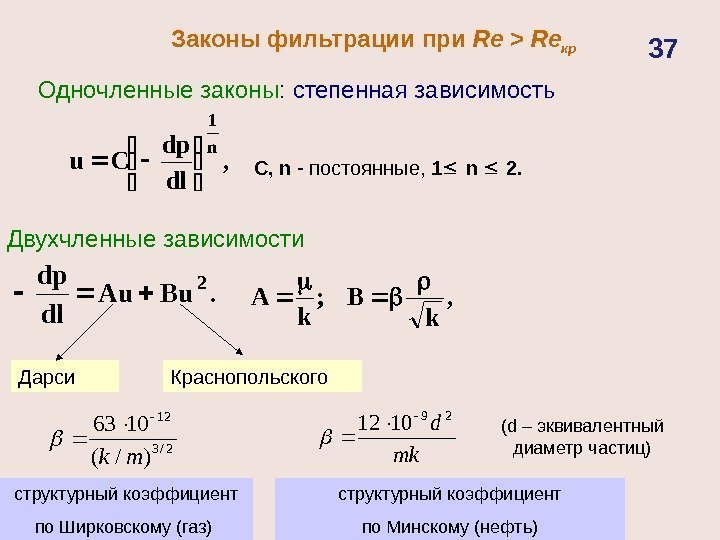
 Законы фильтрации при Re > Re кр Одночленные законы : степенная зависимость, dl dp Cu n 1 C , n — постоянные, 1 n 2. Двухчленные зависимости. Bu. Au dl dp 2 Дарси Краснопольского, k B; k A структурный коэффициент по Минскому (нефть)структурный коэффициент по Ширковскому (газ) 2/3 12 )/( 1063 mk mk d 29 10 12 (d – эквивалентный диаметр частиц)
Законы фильтрации при Re > Re кр Одночленные законы : степенная зависимость, dl dp Cu n 1 C , n — постоянные, 1 n 2. Двухчленные зависимости. Bu. Au dl dp 2 Дарси Краснопольского, k B; k A структурный коэффициент по Минскому (нефть)структурный коэффициент по Ширковскому (газ) 2/3 12 )/( 1063 mk mk d 29 10 12 (d – эквивалентный диаметр частиц)
 ксс к ск Rrh BQ r R kh Q 11 2 ln 2 рр2 2 2 22 22 2 ln ррст c стст ст c кст ск. Q krh p Q r R kh p Решая двухчленное уравнение фильтрации имеем уравнения притока: — для несжимаемой жидкости — для газа
ксс к ск Rrh BQ r R kh Q 11 2 ln 2 рр2 2 2 22 22 2 ln ррст c стст ст c кст ск. Q krh p Q r R kh p Решая двухчленное уравнение фильтрации имеем уравнения притока: — для несжимаемой жидкости — для газа
 ЗАКОНЫ ФИЛЬТРАЦИИ трещинной среды Линейный закон фильтрации Скорость фильтрации : u = m т w. Формула Буссинеска при представлении течения по трещинам, как течения между двумя плоскими параллельными пластинами. dl dp 12 w 2 т Линейный закон фильтрации. dl dp 1 12 Г u 3 ттт = k т –проницаемость трещиноватых сред. pp 1 kk 3 0 *0 mт Для трещиновато-пористой среды общая проницаемость определяется суммой межзерновой и трещинной проницаемостей 39 m т = т Г т ,
ЗАКОНЫ ФИЛЬТРАЦИИ трещинной среды Линейный закон фильтрации Скорость фильтрации : u = m т w. Формула Буссинеска при представлении течения по трещинам, как течения между двумя плоскими параллельными пластинами. dl dp 12 w 2 т Линейный закон фильтрации. dl dp 1 12 Г u 3 ттт = k т –проницаемость трещиноватых сред. pp 1 kk 3 0 *0 mт Для трещиновато-пористой среды общая проницаемость определяется суммой межзерновой и трещинной проницаемостей 39 m т = т Г т ,
 Границы применимости линейного закона фильтрации трещинной среды Значения критических чисел Рейнольдса значительно зависят от шероховатости : • для гладких трещин Re кр =500, • для шероховатых — 0, 4. Если величина относительной шероховатости меньше 0. 065, то её ролью в процессе фильтрации можно пренебречь. Число Re для трещинной среды: 4, 0, mm k 3 u 4 Re тт т кр. Re
Границы применимости линейного закона фильтрации трещинной среды Значения критических чисел Рейнольдса значительно зависят от шероховатости : • для гладких трещин Re кр =500, • для шероховатых — 0, 4. Если величина относительной шероховатости меньше 0. 065, то её ролью в процессе фильтрации можно пренебречь. Число Re для трещинной среды: 4, 0, mm k 3 u 4 Re тт т кр. Re
 ЛЕКЦИЯ
ЛЕКЦИЯ
 Потенциальным течением будем называть течение, при котором проекции массовой скорости на оси ортогональной системы координат будут являться производными некоторой функции по направлениям данных осей. Уравнения потенциального движения ПОТЕНЦИАЛ Cdp k ЗАКОН ДАРСИ через потенциал gradu gradpk u ЗАКОН ДАРСИ
Потенциальным течением будем называть течение, при котором проекции массовой скорости на оси ортогональной системы координат будут являться производными некоторой функции по направлениям данных осей. Уравнения потенциального движения ПОТЕНЦИАЛ Cdp k ЗАКОН ДАРСИ через потенциал gradu gradpk u ЗАКОН ДАРСИ
 УРАВНЕНИЕ ЛАПЛАСА t m 0 Установившееся течение zyx grad div 2 2 2 Уравнение неразрывности 0 udiv t m z f y f x f fdivzyx gradu Телеграфное уравнение
УРАВНЕНИЕ ЛАПЛАСА t m 0 Установившееся течение zyx grad div 2 2 2 Уравнение неразрывности 0 udiv t m z f y f x f fdivzyx gradu Телеграфное уравнение
 Свойства уравнения Лапласа , имеющие большое практическое приложение: сумма частных решений является также решением уравнения Лапласа; произведение частного решения на константу — также решение.
Свойства уравнения Лапласа , имеющие большое практическое приложение: сумма частных решений является также решением уравнения Лапласа; произведение частного решения на константу — также решение.
![Замыкающие соотношения [ , m, k, μ =f(p)] Зависимость плотности от Замыкающие соотношения [ , m, k, μ =f(p)] Зависимость плотности от](http://present5.com/presentforday2/20170114/pgm_prezent_images/pgm_prezent_44.jpg) Замыкающие соотношения [ , m, k, μ =f(p)] Зависимость плотности от давления или уравнения состояния а) Несжимаемая — =со nst. в) Упругая где c — коэффициент объёмного расширения, , V c — объём жидкости; c = (7 -30)10 -10 Па -1 — для нефти и (2, 7 -5)10 -10 Па -1 для пластовой воды. с) Сжимаемая . р = R T — р пл < 9 Мпа; р 9 Мпа где R — газовая постоянная, Т — температура, z — коэффициент сверхсжимаемости. Изотермический процесс — или 0 ррс 0 e dp d 1 dp d. V V 1 Т с с с ст ст р р ст ст ст рz рz
Замыкающие соотношения [ , m, k, μ =f(p)] Зависимость плотности от давления или уравнения состояния а) Несжимаемая — =со nst. в) Упругая где c — коэффициент объёмного расширения, , V c — объём жидкости; c = (7 -30)10 -10 Па -1 — для нефти и (2, 7 -5)10 -10 Па -1 для пластовой воды. с) Сжимаемая . р = R T — р пл < 9 Мпа; р 9 Мпа где R — газовая постоянная, Т — температура, z — коэффициент сверхсжимаемости. Изотермический процесс — или 0 ррс 0 e dp d 1 dp d. V V 1 Т с с с ст ст р р ст ст ст рz рz
 Зависимость пористости от давления эф +р пл =р горн =const р горн = горн g H – горное давление 00 рр mmm Зависимость вязкости и проницаемости от давления 0 ррa 0 e 0 ррka 0 ekk При р < 10 Мпа показатель в выше приведенных экспоненциальных зависимостях меньше 1 и, следовательно, данные зависимости можно разложить в ряд Тейлора. Ограничиваясь первыми двумя членами, получаем где — общее обозначение выше приведённых параметров. 00 ррa
Зависимость пористости от давления эф +р пл =р горн =const р горн = горн g H – горное давление 00 рр mmm Зависимость вязкости и проницаемости от давления 0 ррa 0 e 0 ррka 0 ekk При р < 10 Мпа показатель в выше приведенных экспоненциальных зависимостях меньше 1 и, следовательно, данные зависимости можно разложить в ряд Тейлора. Ограничиваясь первыми двумя членами, получаем где — общее обозначение выше приведённых параметров. 00 ррa
 Начальные и граничные условия Начальные условия = о ( x , y , z ) при t =0 Если при t =0 пласт не возмущён, то = о = const. Граничные условия Внешняя граница : 1)постоянный потенциал (Г, t )= к = const — контур питания ; 2) постоянный расход G = F u = const или 3) переменный поток массы через границу 4) замкнутая внешняя граница 5) бесконечный пласт lim x (Г, t )= к = const y ; const n ); t(f n 1 ; 0 n
Начальные и граничные условия Начальные условия = о ( x , y , z ) при t =0 Если при t =0 пласт не возмущён, то = о = const. Граничные условия Внешняя граница : 1)постоянный потенциал (Г, t )= к = const — контур питания ; 2) постоянный расход G = F u = const или 3) переменный поток массы через границу 4) замкнутая внешняя граница 5) бесконечный пласт lim x (Г, t )= к = const y ; const n ); t(f n 1 ; 0 n
 Внутренняя граница 1) постоянный потенциал (r c , t)= c =const 2) постоянный массовый дебит 3) переменный потенциал на забое ( r c , t )= f 2 ( t ) при r = r c ; 4) переменный массовый дебит 5) не работающая скважинаccc rr при h 2 G rr или const rhr 2 uf. G c 3 rr при • (t)f r r . rr при • 0 r rc
Внутренняя граница 1) постоянный потенциал (r c , t)= c =const 2) постоянный массовый дебит 3) переменный потенциал на забое ( r c , t )= f 2 ( t ) при r = r c ; 4) переменный массовый дебит 5) не работающая скважинаccc rr при h 2 G rr или const rhr 2 uf. G c 3 rr при • (t)f r r . rr при • 0 r rc
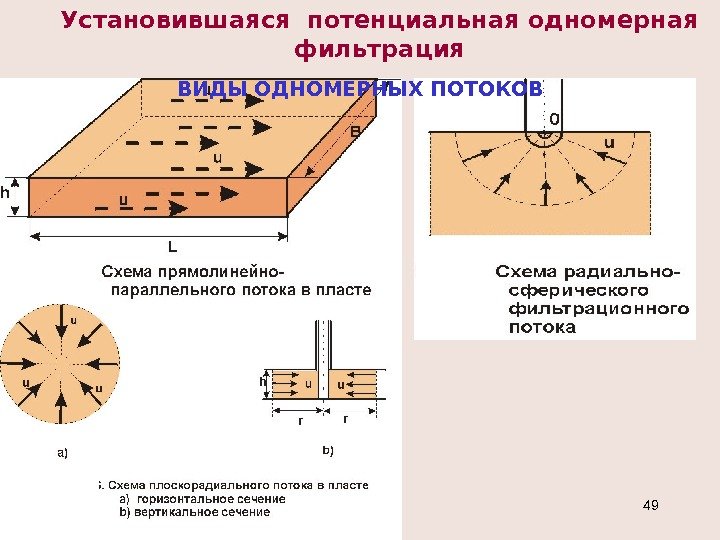
 Установившаяся потенциальная одномерная фильтрация ВИДЫ ОДНОМЕРНЫХ ПОТОКОВ
Установившаяся потенциальная одномерная фильтрация ВИДЫ ОДНОМЕРНЫХ ПОТОКОВ
 ИССЛЕДОВАНИЕ ОДНОМЕРНЫХ ТЕЧЕНИЙ Задача исследования установившегося фильтрационного потока заключается в определении дебита (расхода), давления, градиента давления и скорости фильтрации в любой точке потока, а также в установлении закона движения частиц жидкости (или газа) вдоль их траекторий и в определении средневзвешенного по объёму порового пространства пластового давления.
ИССЛЕДОВАНИЕ ОДНОМЕРНЫХ ТЕЧЕНИЙ Задача исследования установившегося фильтрационного потока заключается в определении дебита (расхода), давления, градиента давления и скорости фильтрации в любой точке потока, а также в установлении закона движения частиц жидкости (или газа) вдоль их траекторий и в определении средневзвешенного по объёму порового пространства пластового давления.
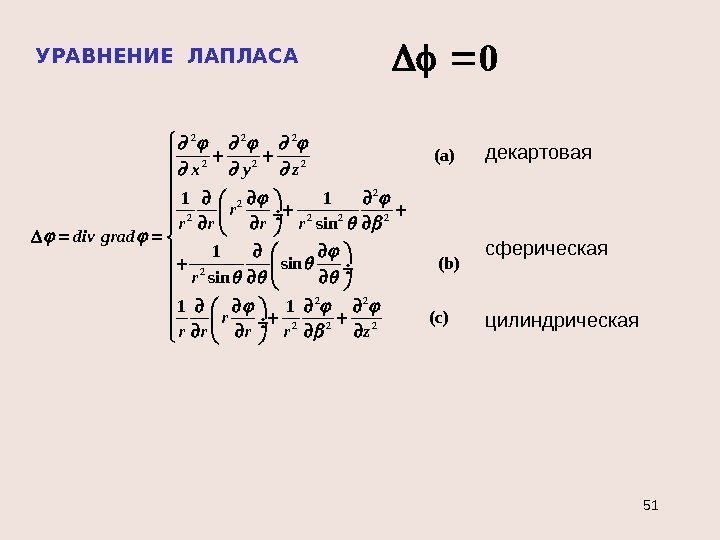
 2 2 2 2 21 1 sin (a) (b) (c)1 1 r r r x y z div gr r r rd za r УРАВНЕНИЕ ЛАПЛАСА 0 декартовая сферическая цилиндрическая
2 2 2 2 21 1 sin (a) (b) (c)1 1 r r r x y z div gr r r rd za r УРАВНЕНИЕ ЛАПЛАСА 0 декартовая сферическая цилиндрическая
 Решение общего дифференциального уравнения Показатель формы потока Начало системы координат : • галерея (для прямолинейно- параллельного потока); • центр контура скважины в плоскости подошвы пласта (для плоско-радиального потока); • центр полусферического забоя скважины (для сферически-радиального потока). Для укрупнённой трубки тока u= G /F( r ), где F = F ( r ) — площадь эквипотенциальной поверхности прямолинейно-параллельный поток — F ( r )= Bh ; плоско-радиальный поток — F ( r ) =2 h r ; радиально-сферический поток — F ( r ) = 2 r 2. G>0 — эксплуатационная скважина
Решение общего дифференциального уравнения Показатель формы потока Начало системы координат : • галерея (для прямолинейно- параллельного потока); • центр контура скважины в плоскости подошвы пласта (для плоско-радиального потока); • центр полусферического забоя скважины (для сферически-радиального потока). Для укрупнённой трубки тока u= G /F( r ), где F = F ( r ) — площадь эквипотенциальной поверхности прямолинейно-параллельный поток — F ( r )= Bh ; плоско-радиальный поток — F ( r ) =2 h r ; радиально-сферический поток — F ( r ) = 2 r 2. G>0 — эксплуатационная скважина
 Уравнение Дарси через расход j Ar G drd прямолинейно-параллельный поток — A = Bh , j =0 ; плоско-радиальный поток — A =2 h , j =1 ; радиально-сферический поток — A = 2 , j =2. j — показатель формы потока, т. к. характеризует вид одномерного течения. Уравнение для потенциала ( j =0; 2)C j 1 r A G j 1 Уравнение для потенциала ( j =1) Cr ln h 2 G
Уравнение Дарси через расход j Ar G drd прямолинейно-параллельный поток — A = Bh , j =0 ; плоско-радиальный поток — A =2 h , j =1 ; радиально-сферический поток — A = 2 , j =2. j — показатель формы потока, т. к. характеризует вид одномерного течения. Уравнение для потенциала ( j =0; 2)C j 1 r A G j 1 Уравнение для потенциала ( j =1) Cr ln h 2 G
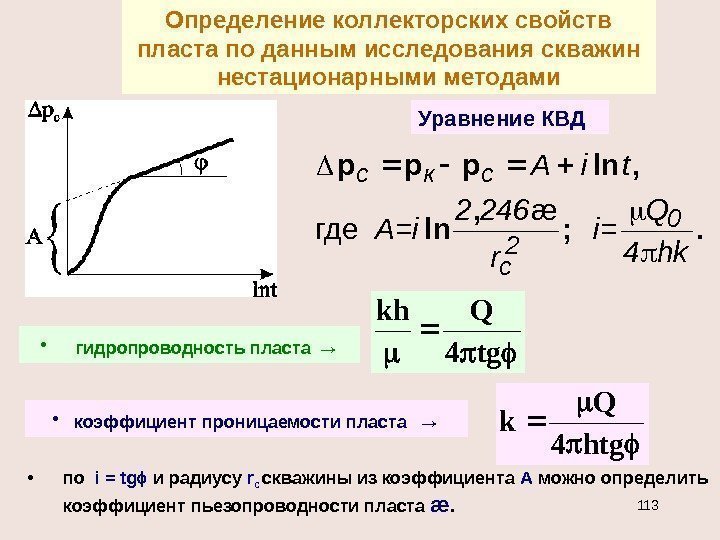
 r r ln a где , r r lna к ск к к ; rr j 1 AG j 1 c j 1 к cк Выражение для дебита при постоянных потенциалах на границах ( j =0; 2) , r r ln h 2 G c к ск ( j =1 Уравнение для потенциала ( j =0; 2) Уравнение для потенциала ( j =1) j 1 с j 1 к ск j 1 j 1 кк rr a где , rr a
r r ln a где , r r lna к ск к к ; rr j 1 AG j 1 c j 1 к cк Выражение для дебита при постоянных потенциалах на границах ( j =0; 2) , r r ln h 2 G c к ск ( j =1 Уравнение для потенциала ( j =0; 2) Уравнение для потенциала ( j =1) j 1 с j 1 к ск j 1 j 1 кк rr a где , rr a
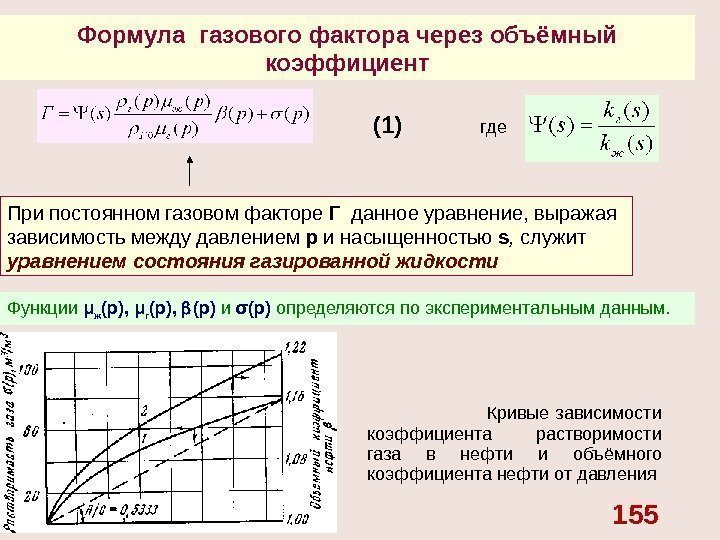
 № Вид коллектора Характери- стики Вид флюида Характеристики Потенциал 1 Недеформируемый (пористый) пласт k = const Несжимаемая жидкость = const ; μ= const 4 Недеформируемый (пористый) пласт k = const Совершенный газ = cт р/ р ст -изотермическое течение; μ = const 5 Недеформируемый (пористый) пласт k = const Реальный газ — изотермическое течение. ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ Cdp k Cp k Ср p 2 k 2 стст р= z R T – общий случай; μ =const; )p(z 1 р р ст ст C)p(f p k ст ст pdp)p(z)p()p(f 1 C z 2 p f 2 2 2 CT CT k k k dp C p C p p
№ Вид коллектора Характери- стики Вид флюида Характеристики Потенциал 1 Недеформируемый (пористый) пласт k = const Несжимаемая жидкость = const ; μ= const 4 Недеформируемый (пористый) пласт k = const Совершенный газ = cт р/ р ст -изотермическое течение; μ = const 5 Недеформируемый (пористый) пласт k = const Реальный газ — изотермическое течение. ПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ Cdp k Cp k Ср p 2 k 2 стст р= z R T – общий случай; μ =const; )p(z 1 р р ст ст C)p(f p k ст ст pdp)p(z)p()p(f 1 C z 2 p f 2 2 2 CT CT k k k dp C p C p p
 2 Трещиноватый (деформируемый) пласт Несжимаемая жидкость = const ; μ = const 3 Недеформируемый (пористый) пласт k = const Упругая жидкость μ = const. Cрр1 4 k 4 0 * * 0 m 0 ррж 0 e dpd ж С k ж 3 0 *0 mрр1 kk
2 Трещиноватый (деформируемый) пласт Несжимаемая жидкость = const ; μ = const 3 Недеформируемый (пористый) пласт k = const Упругая жидкость μ = const. Cрр1 4 k 4 0 * * 0 m 0 ррж 0 e dpd ж С k ж 3 0 *0 mрр1 kk
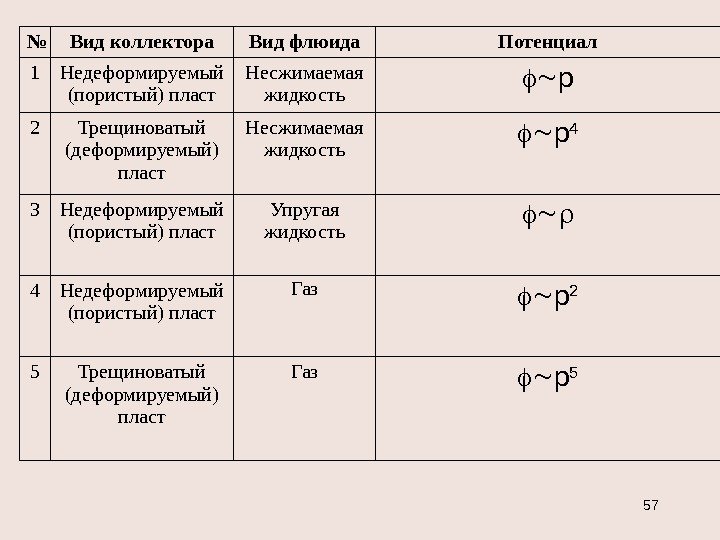
 № Вид коллектора Вид флюида Потенциал 1 Недеформируемый (пористый) пласт Несжимаемая жидкость p 2 Трещиноватый (деформируемый) пласт Несжимаемая жидкость p 4 3 Недеформируемый (пористый) пласт Упругая жидкость 4 Недеформируемый (пористый) пласт Газ p 2 5 Трещиноватый (деформируемый) пласт Газ p
№ Вид коллектора Вид флюида Потенциал 1 Недеформируемый (пористый) пласт Несжимаемая жидкость p 2 Трещиноватый (деформируемый) пласт Несжимаемая жидкость p 4 3 Недеформируемый (пористый) пласт Упругая жидкость 4 Недеформируемый (пористый) пласт Газ p 2 5 Трещиноватый (деформируемый) пласт Газ p
 Анализ основных видов одномерного течения по закону Дарси Течение несжимаемой жидкости через недеформируемый (пористый) пласт / плоско-радиальное течение/ Cp k
Анализ основных видов одномерного течения по закону Дарси Течение несжимаемой жидкости через недеформируемый (пористый) пласт / плоско-радиальное течение/ Cp k
 Функции плоско-радиальное Распределение давления Градиент давления
Функции плоско-радиальное Распределение давления Градиент давления
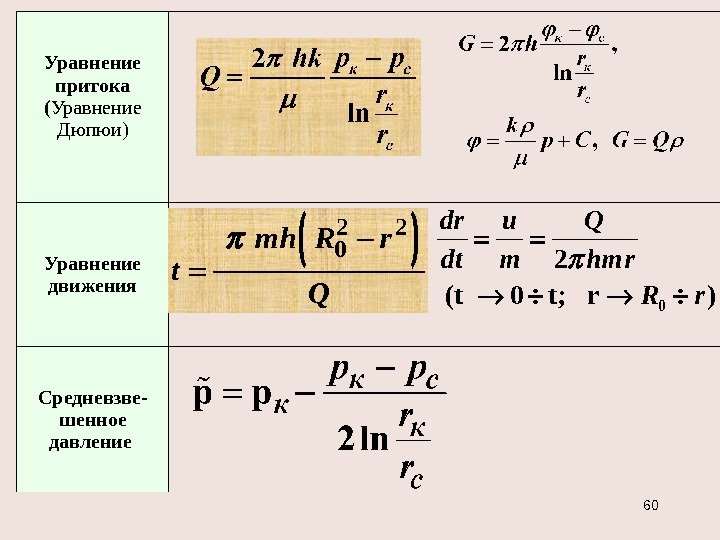
 Уравнение притока ( Уравнение Дюпюи) Уравнение движения Средневзве- шенное давление 2 2 0 mh R r t Q 0 2 (t 0 t; r ) dr u Q dt m hmr R r
Уравнение притока ( Уравнение Дюпюи) Уравнение движения Средневзве- шенное давление 2 2 0 mh R r t Q 0 2 (t 0 t; r ) dr u Q dt m hmr R r
 Средневзвешенное давление
Средневзвешенное давление
 Средневзвешенное давление
Средневзвешенное давление
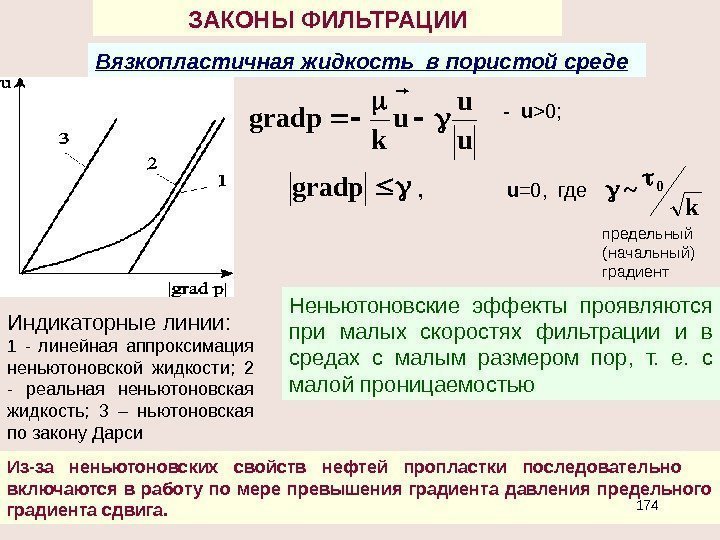
 1. Дебит не зависит от r , а только от депрессии d р. График зависимости Q от d р называется индикаторной диаграммой , а сама зависимость — индикаторной. Коэффициент продуктивности скважины 2. Градиент давления и, следовательно, скорость фильтрации обратно пропорциональны расстоянию и образуют гиперболу с резким возрастанием значений приближении к забою. Анализ: Па cм p Q K 3 к
1. Дебит не зависит от r , а только от депрессии d р. График зависимости Q от d р называется индикаторной диаграммой , а сама зависимость — индикаторной. Коэффициент продуктивности скважины 2. Градиент давления и, следовательно, скорость фильтрации обратно пропорциональны расстоянию и образуют гиперболу с резким возрастанием значений приближении к забою. Анализ: Па cм p Q K 3 к
 4. Изобары — концентрические, цилиндрические поверх — ности, ортогональные траекториям. 5. Дебит слабо зависит от величины радиуса контура r к для достаточно больших значений r к / r c , т. к. r к / r c входят в формулу под знаком логарифма. 3. Графиком зависимости р=р( r ) является логарифмическая кривая, вращением которой вокруг оси скважины образуется поверхность, называемая воронкой депрессии.
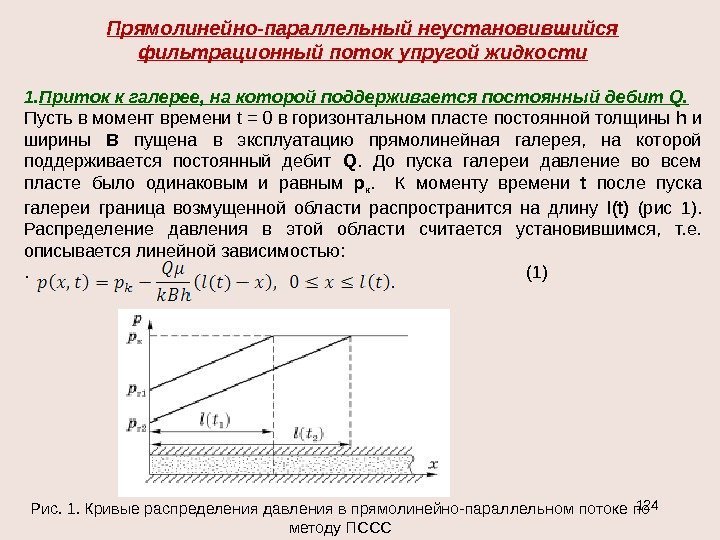
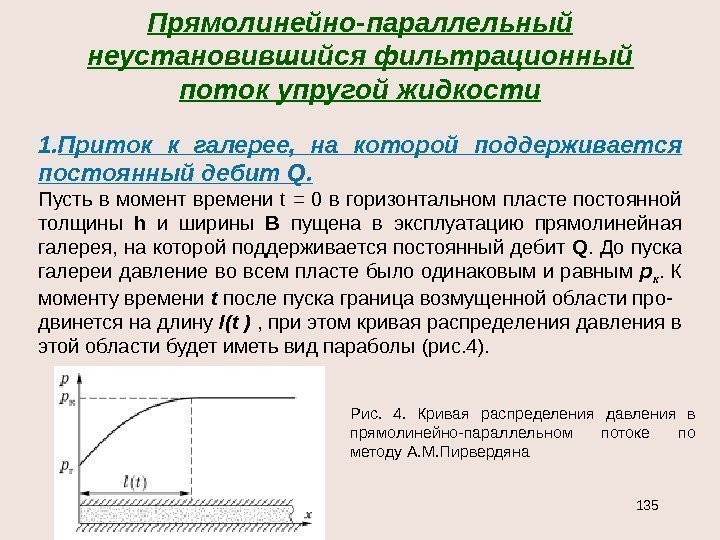
4. Изобары — концентрические, цилиндрические поверх — ности, ортогональные траекториям. 5. Дебит слабо зависит от величины радиуса контура r к для достаточно больших значений r к / r c , т. к. r к / r c входят в формулу под знаком логарифма. 3. Графиком зависимости р=р( r ) является логарифмическая кривая, вращением которой вокруг оси скважины образуется поверхность, называемая воронкой депрессии.
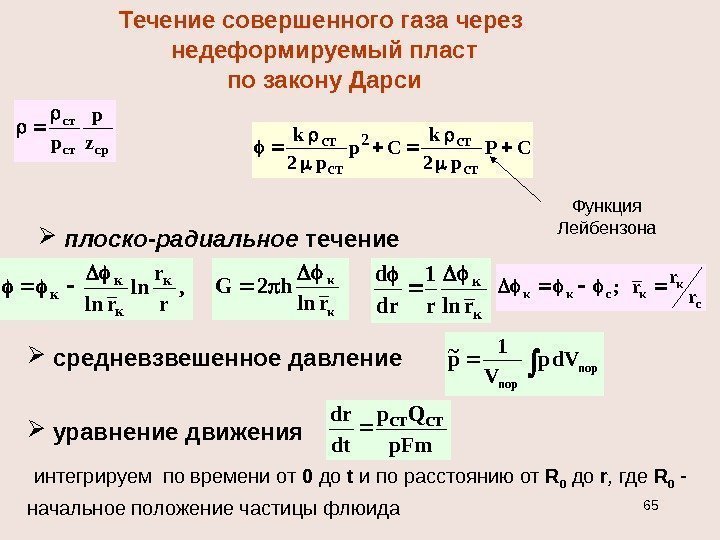
 Течение совершенного газа через недеформируемый пласт по закону Дарси. СР p 2 k Ср p 2 k ст ст2 ст ст плоско-радиальное течение , r r ln rln к кк к rln h 2 G к к rlnr 1 dr d с кксккr rr; средневзвешенное давление пор d. Vр V 1 р~ уравнение движения интегрируем по времени от 0 до t и по расстоянию от R 0 до r , где R 0 — начальное положение частицы флюида р. Fm Qр dt drстстcpстc т z р р Функция Лейбензона
Течение совершенного газа через недеформируемый пласт по закону Дарси. СР p 2 k Ср p 2 k ст ст2 ст ст плоско-радиальное течение , r r ln rln к кк к rln h 2 G к к rlnr 1 dr d с кксккr rr; средневзвешенное давление пор d. Vр V 1 р~ уравнение движения интегрируем по времени от 0 до t и по расстоянию от R 0 до r , где R 0 — начальное положение частицы флюида р. Fm Qр dt drстстcpстc т z р р Функция Лейбензона
 Распределения плоско-радиальное Распределение давления Р=р 2 Градиент давления Уравнение притока Уравнение движения Средневзвешенн ое давлениеpr 2 1 а dr рd 1 a р hk Q ст cт ст 22 0 Q r. Rmh t r 2 к с к rln 4 р р 1 1 рр ~ c к кк к r r r; rln P 1 a, r r ln 1 a. PP
Распределения плоско-радиальное Распределение давления Р=р 2 Градиент давления Уравнение притока Уравнение движения Средневзвешенн ое давлениеpr 2 1 а dr рd 1 a р hk Q ст cт ст 22 0 Q r. Rmh t r 2 к с к rln 4 р р 1 1 рр ~ c к кк к r r r; rln P 1 a, r r ln 1 a. PP
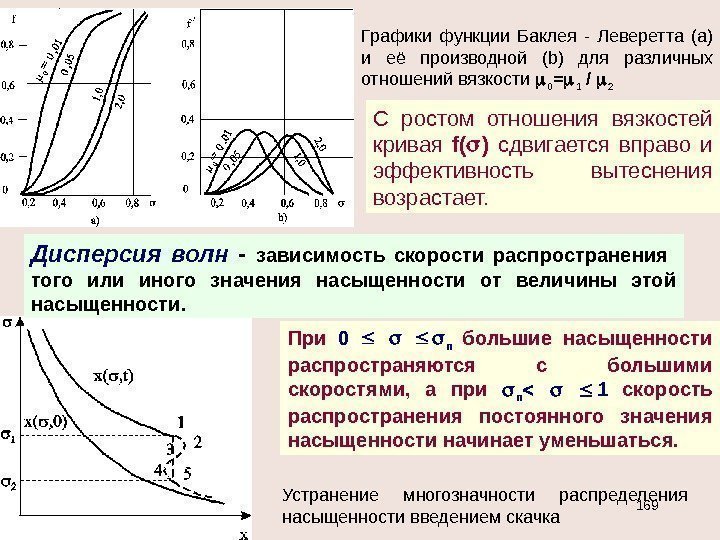
 Анализ – плоско-радиальное течение Распределение давления в недеформируемом пласте 1 — газ; 2 — несжимаемая жидкость Пьезометрическая кривая для газа имеет более пологий характер на большем своём протяжении, чем кривая несжимаемой жидкости; однако у неё более резкое изменение у стенки скважины, чем для несжимаемой жидкости. Распределение давления
Анализ – плоско-радиальное течение Распределение давления в недеформируемом пласте 1 — газ; 2 — несжимаемая жидкость Пьезометрическая кривая для газа имеет более пологий характер на большем своём протяжении, чем кривая несжимаемой жидкости; однако у неё более резкое изменение у стенки скважины, чем для несжимаемой жидкости. Распределение давления
 Индикаторная зависимость при фильтрации газа по закону Дарси в переменных Q – Δ p Уравнение притока . rln р р hk Q к 2 к ст ст Индикаторная зависимость для газа —параболическая зависимость дебита Q ст от депрессии р к ( с осью, параллельной оси дебитов ) и линейная зависимость дебита от разницы квадратов пластового и забойного давлений. 2 кккстр р р2 Q т. к. р к 2 — р с 2 = 2 р к р с — ( р с ) 2 (где р с = р к — р с ) Индикаторная зависимость при фильтрации газа по закону Дарси в переменных Q – Δ p
Индикаторная зависимость при фильтрации газа по закону Дарси в переменных Q – Δ p Уравнение притока . rln р р hk Q к 2 к ст ст Индикаторная зависимость для газа —параболическая зависимость дебита Q ст от депрессии р к ( с осью, параллельной оси дебитов ) и линейная зависимость дебита от разницы квадратов пластового и забойного давлений. 2 кккстр р р2 Q т. к. р к 2 — р с 2 = 2 р к р с — ( р с ) 2 (где р с = р к — р с ) Индикаторная зависимость при фильтрации газа по закону Дарси в переменных Q – Δ p
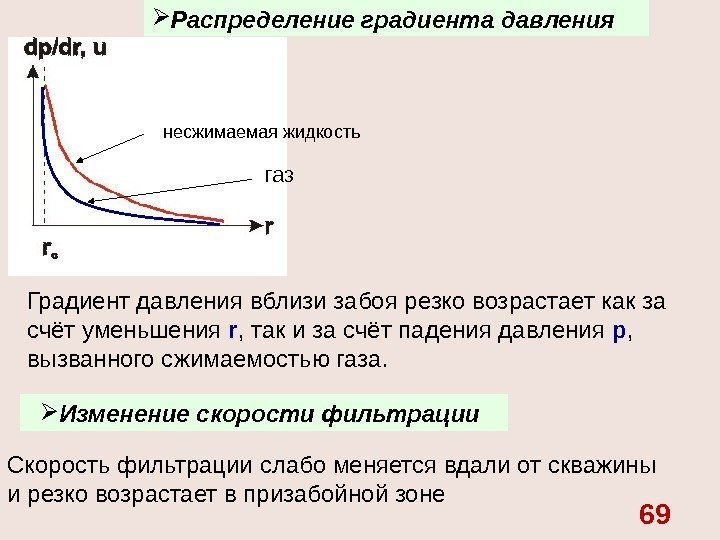
 Распределение градиента давления Градиент давления вблизи забоя резко возрастает как за счёт уменьшения r , так и за счёт падения давления р , вызванного сжимаемостью газа. Изменение скорости фильтрации Скорость фильтрации слабо меняется вдали от скважины и резко возрастает в призабойной зоне несжимаемая жидкость газ
Распределение градиента давления Градиент давления вблизи забоя резко возрастает как за счёт уменьшения r , так и за счёт падения давления р , вызванного сжимаемостью газа. Изменение скорости фильтрации Скорость фильтрации слабо меняется вдали от скважины и резко возрастает в призабойной зоне несжимаемая жидкость газ
 Течение несжимаемой жидкости в трещиноватом (деформируемом) пласте Потенциальная функция Cdpk Трещиноватый (деформируемый) пласт Не сжимаемая жидкость = const ; μ = const РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ
Течение несжимаемой жидкости в трещиноватом (деформируемом) пласте Потенциальная функция Cdpk Трещиноватый (деформируемый) пласт Не сжимаемая жидкость = const ; μ = const РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ
 ГРАДИЕНТ ДАВЛЕНИЯ 2 d G dr hr Объёмный дебит G Q
ГРАДИЕНТ ДАВЛЕНИЯ 2 d G dr hr Объёмный дебит G Q
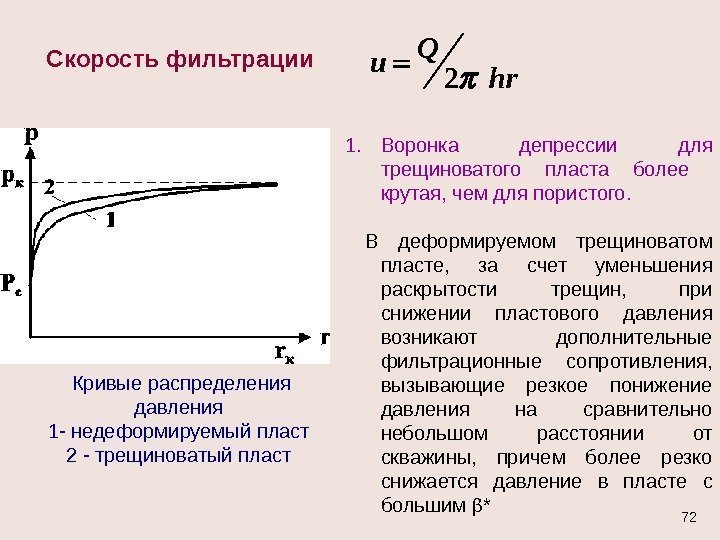
 Скорость фильтрации 2 Q u hr Кривые распределения давления 1 — недеформируемый пласт 2 — трещиноватый пласт 1. Воронка депрессии для трещиноватого пласта более крутая, чем для пористого. В деформируемом трещиноватом пласте, за счет уменьшения раскрытости трещин, при снижении пластового давления возникают дополнительные фильтрационные сопротивления, вызывающие резкое понижение давления на сравнительно небольшом расстоянии от скважины, причем более резко снижается давление в пласте с большим *
Скорость фильтрации 2 Q u hr Кривые распределения давления 1 — недеформируемый пласт 2 — трещиноватый пласт 1. Воронка депрессии для трещиноватого пласта более крутая, чем для пористого. В деформируемом трещиноватом пласте, за счет уменьшения раскрытости трещин, при снижении пластового давления возникают дополнительные фильтрационные сопротивления, вызывающие резкое понижение давления на сравнительно небольшом расстоянии от скважины, причем более резко снижается давление в пласте с большим *
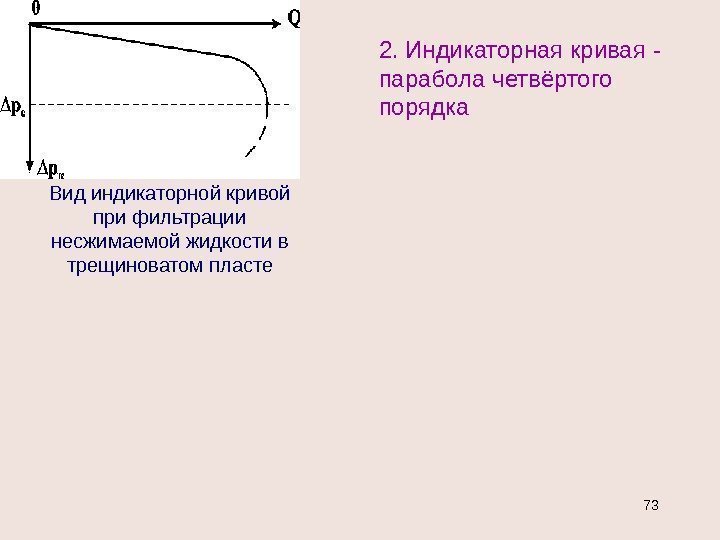
 2. Индикаторная кривая — парабола четвёртого порядка Вид индикаторной кривой при фильтрации несжимаемой жидкости в трещиноватом пласте
2. Индикаторная кривая — парабола четвёртого порядка Вид индикаторной кривой при фильтрации несжимаемой жидкости в трещиноватом пласте
 Анализ одномерных потоков при нелинейных законах фильтрации 2 buu kdrdp k b где
Анализ одномерных потоков при нелинейных законах фильтрации 2 buu kdrdp k b где
 Течение несжимаемой жидкости в недеформируемом пласте 22 rh 2 Q b rh 2 Q kdrdp Уравнение фильтрации при u=Q / (2 rh) Распределение давления в пласте Уравнение притока к 2 2 к к R 1 r 1 h 2 b. Q r R ln kh 2 Q рр кс22 с к ск R 1 r 1 h 2 b. Q r. R ln kh 2 Q рр • Дебит — положительный корень уравнения притока • Индикаторная линия — парабола. • Кривая распределения давления — гипербола и воронка депрессии — гипербола вращения. • Крутизна воронки депрессии у стенки скважины больше, чем у чисто логарифмической кривой при течении по закону Дарси.
Течение несжимаемой жидкости в недеформируемом пласте 22 rh 2 Q b rh 2 Q kdrdp Уравнение фильтрации при u=Q / (2 rh) Распределение давления в пласте Уравнение притока к 2 2 к к R 1 r 1 h 2 b. Q r R ln kh 2 Q рр кс22 с к ск R 1 r 1 h 2 b. Q r. R ln kh 2 Q рр • Дебит — положительный корень уравнения притока • Индикаторная линия — парабола. • Кривая распределения давления — гипербола и воронка депрессии — гипербола вращения. • Крутизна воронки депрессии у стенки скважины больше, чем у чисто логарифмической кривой при течении по закону Дарси.
 Идеальный газ в недеформируемом пласте 2 ст222 стст ст ст Q prkh 4 p Q khpr 2 p drdp Уравнение фильтрации т. к rhp 2 p. Q rh 2 p p Q f G uстст стст r 1 Q kh 2 p r r ln. Q kh p рр c 2 ст22 стст c ст ст2 с 2 Распределение давления отличается от распределения давления по закону Дарси наличием последнего члена, что диктует более резкое изменение давления в призабойной зоне.
Идеальный газ в недеформируемом пласте 2 ст222 стст ст ст Q prkh 4 p Q khpr 2 p drdp Уравнение фильтрации т. к rhp 2 p. Q rh 2 p p Q f G uстст стст r 1 Q kh 2 p r r ln. Q kh p рр c 2 ст22 стст c ст ст2 с 2 Распределение давления отличается от распределения давления по закону Дарси наличием последнего члена, что диктует более резкое изменение давления в призабойной зоне.
 Уравнение притока 2 ст c 22 стст c к ст ст2 с 2 к. Q krh 2 p r R ln. Q kh p рр 2 стст 2 с 2 к. ВQАQрр Коэффициенты А и В определяют по данным исследования газовых скважин при установившихся режимах. или
Уравнение притока 2 ст c 22 стст c к ст ст2 с 2 к. Q krh 2 p r R ln. Q kh p рр 2 стст 2 с 2 к. ВQАQрр Коэффициенты А и В определяют по данным исследования газовых скважин при установившихся режимах. или
 Однородная несжимаемая жидкость в деформируемом (трещиноватом) пласте Закон фильтрации, ubua l р2 где ттблт km 1120 l 69, 1 b ; k 1 a Уравнение притока через давление и объемный дебит кcтт бл cк mк rr h. G mk l rr hk G 11 1 120 69, 1 ln 2 р
Однородная несжимаемая жидкость в деформируемом (трещиноватом) пласте Закон фильтрации, ubua l р2 где ттблт km 1120 l 69, 1 b ; k 1 a Уравнение притока через давление и объемный дебит кcтт бл cк mк rr h. G mk l rr hk G 11 1 120 69, 1 ln 2 р
 Индикаторная кривая — результат сложения двух парабол: параболы четвёртого порядка , симметричной относительно оси, параллельной оси дебитов, и параболы второго порядка (относительно дебита Q ) симметричной относительно оси, параллельной оси депрессий ( р с ) и отстоящей от последней на расстояние кc бл c к т r 1 l r r lnm 1 h
Индикаторная кривая — результат сложения двух парабол: параболы четвёртого порядка , симметричной относительно оси, параллельной оси дебитов, и параболы второго порядка (относительно дебита Q ) симметричной относительно оси, параллельной оси депрессий ( р с ) и отстоящей от последней на расстояние кc бл c к т r 1 l r r lnm 1 h
 Идеальный газ в деформируемом (трещиноватом) пласте 22 21 120 69, 1 2 hr. G ml hr. G drd òáëò Закон фильтрации в дифференциальной форме через потенциал кcтбл cк кк кк ст т rrh Q m l r r h Q p p k 11 1120 69, 1 ln 2 р 1 5 р р 11 20 1 4 22 44 20 Уравнение притока через давление и объемный дебит
Идеальный газ в деформируемом (трещиноватом) пласте 22 21 120 69, 1 2 hr. G ml hr. G drd òáëò Закон фильтрации в дифференциальной форме через потенциал кcтбл cк кк кк ст т rrh Q m l r r h Q p p k 11 1120 69, 1 ln 2 р 1 5 р р 11 20 1 4 22 44 20 Уравнение притока через давление и объемный дебит
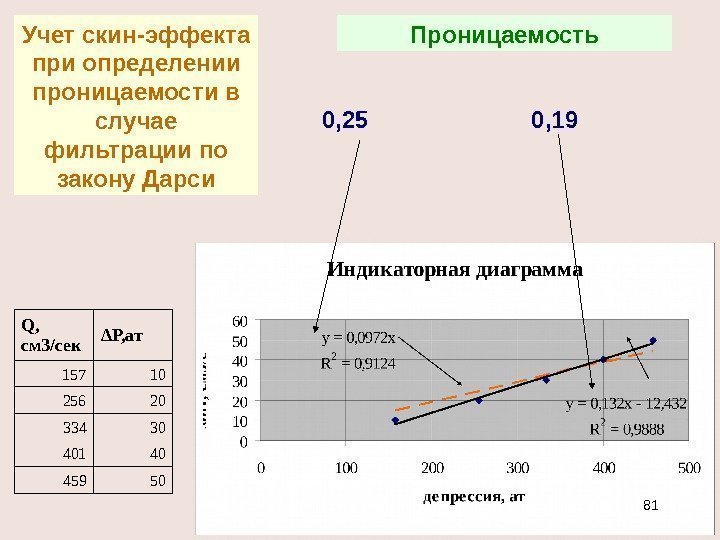
 Учет скин-эффекта при определении проницаемости в случае фильтрации по закону Дарси Q, cм 3/сек ΔР, ат 157 10 256 20 334 30 401 40 459 50 Проницаемость 0, 25 0,
Учет скин-эффекта при определении проницаемости в случае фильтрации по закону Дарси Q, cм 3/сек ΔР, ат 157 10 256 20 334 30 401 40 459 50 Проницаемость 0, 25 0,
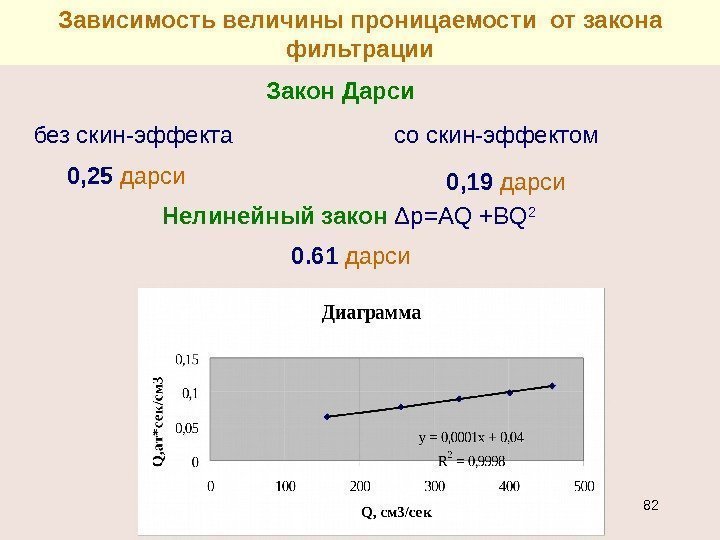
 Зависимость величины проницаемости от закона фильтрации Закон Дарси без скин-эффекта со скин-эффектом 0, 25 дарси 0, 19 дарси Нелинейный закон Δ р= AQ +BQ 2 0. 61 дарси
Зависимость величины проницаемости от закона фильтрации Закон Дарси без скин-эффекта со скин-эффектом 0, 25 дарси 0, 19 дарси Нелинейный закон Δ р= AQ +BQ 2 0. 61 дарси

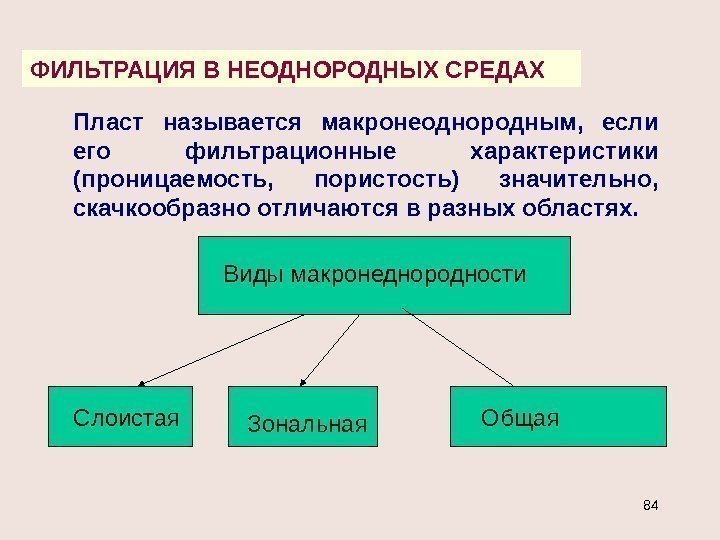
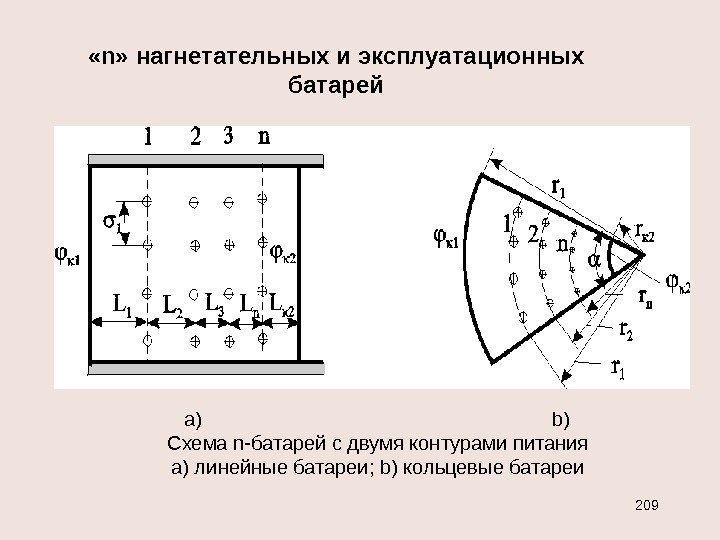
 ФИЛЬТРАЦИЯ В НЕОДНОРОДНЫХ СРЕДАХ Пласт называется макронеоднородным, если его фильтрационные характеристики (проницаемость, пористость) значительно, скачкообразно отличаются в разных областях. Виды макронеднородности Слоистая Зональная Общая
ФИЛЬТРАЦИЯ В НЕОДНОРОДНЫХ СРЕДАХ Пласт называется макронеоднородным, если его фильтрационные характеристики (проницаемость, пористость) значительно, скачкообразно отличаются в разных областях. Виды макронеднородности Слоистая Зональная Общая
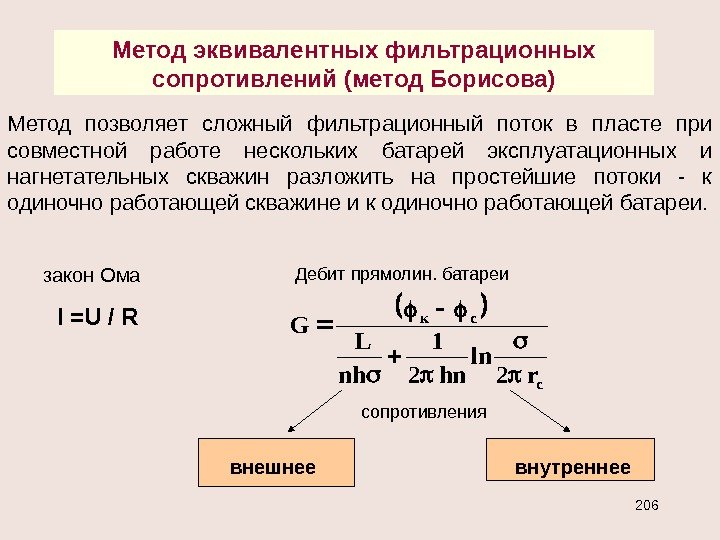
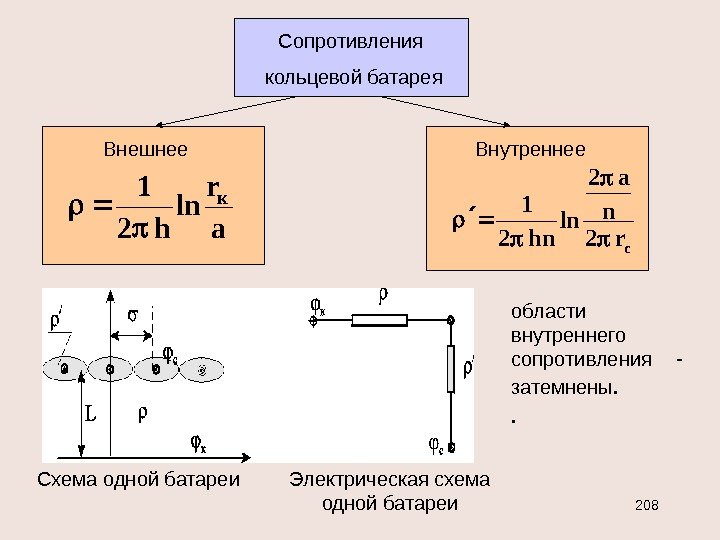
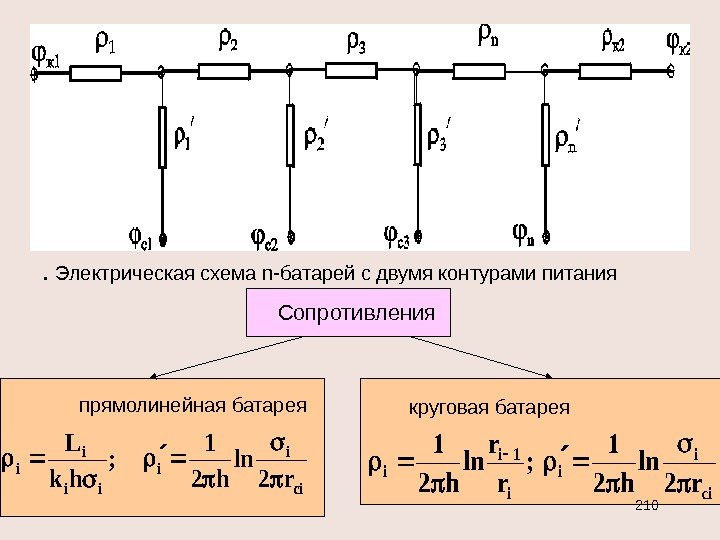
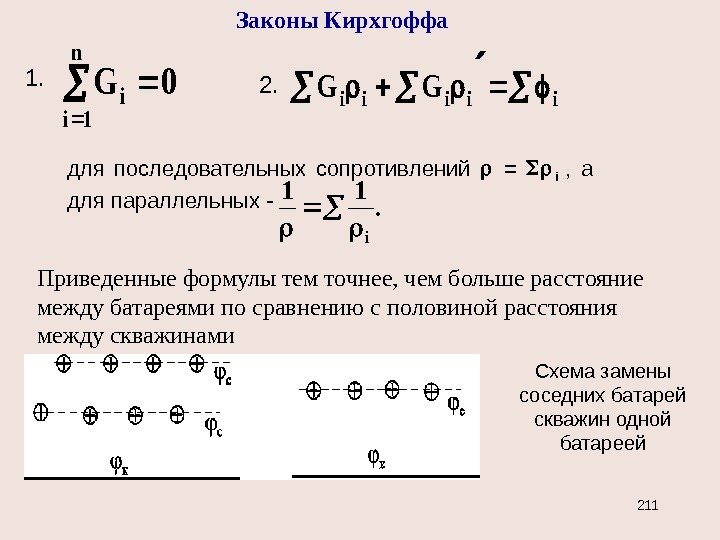
 ; cк cк rr Bh. G , ln 2 c к ск r r h. G прямолинейно-параллельный поток плоско-радиальный поток Cp k закон Ома I = U / R R pp G cк /Bhk l R /2 ln hk r r R c к для последовательных сопротивлений R = R i для параллельных — . 11 i. RR
; cк cк rr Bh. G , ln 2 c к ск r r h. G прямолинейно-параллельный поток плоско-радиальный поток Cp k закон Ома I = U / R R pp G cк /Bhk l R /2 ln hk r r R c к для последовательных сопротивлений R = R i для параллельных — . 11 i. RR
 Многослойный пласт — неоднородность по толщине пласта. Пропластки — гидравлически изолированы, либо гидравлически сообщающиеся. В пределах каждого пропластка фильтрационные параметры постоянны, а на границе соседних они претерпевают скачок. Если течение потенциально, то полный дебит пласта определяется как сумма дебитов всех пропластков. Квазиоднородное приближение : СЛОИСТАЯ НЕОДНОРОДНОСТЬ i ii cp h hk k
Многослойный пласт — неоднородность по толщине пласта. Пропластки — гидравлически изолированы, либо гидравлически сообщающиеся. В пределах каждого пропластка фильтрационные параметры постоянны, а на границе соседних они претерпевают скачок. Если течение потенциально, то полный дебит пласта определяется как сумма дебитов всех пропластков. Квазиоднородное приближение : СЛОИСТАЯ НЕОДНОРОДНОСТЬ i ii cp h hk k
 ЗОНАЛЬНАЯ НЕОДНОРОДНОСТЬ Пласт по площади состоит из нескольких зон различных фильтрационных параметров, на границах которых данные параметры меняются скачкообразно. Массовый дебит постоянен и равен: при плоскорадиальном потоке i 1 i i i ск r r ln k 1 h 2 G dp 1 Квазиоднородное приближение : i iicp kl. L k i 1 i i i c к cp r r ln k 1 r. R ln k
ЗОНАЛЬНАЯ НЕОДНОРОДНОСТЬ Пласт по площади состоит из нескольких зон различных фильтрационных параметров, на границах которых данные параметры меняются скачкообразно. Массовый дебит постоянен и равен: при плоскорадиальном потоке i 1 i i i ск r r ln k 1 h 2 G dp 1 Квазиоднородное приближение : i iicp kl. L k i 1 i i i c к cp r r ln k 1 r. R ln k
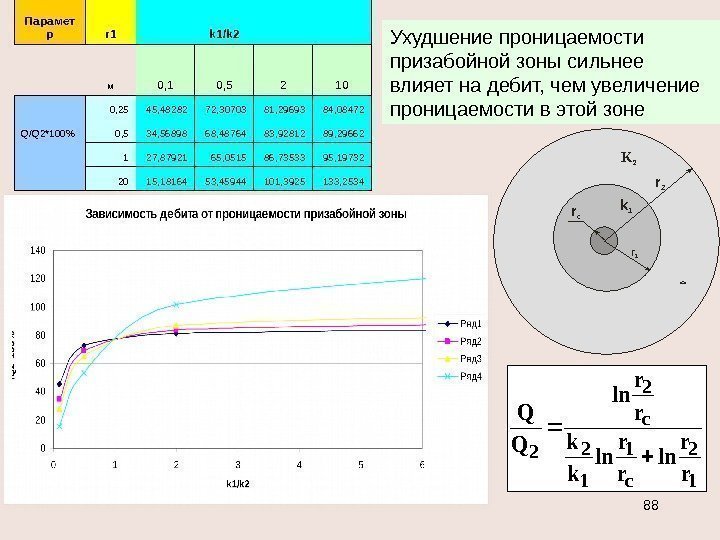
 Парамет р r 1 k 1/k 2 м 0, 1 0, 5 2 10 0, 25 45, 48282 72, 30703 81, 29693 84, 08472 Q/Q 2*100% 0, 5 34, 56898 68, 48764 83, 92812 89, 29662 1 27, 87921 65, 0515 86, 73533 95, 19732 20 15, 18164 53, 45944 101, 3925 133, 2534 Ухудшение проницаемости призабойной зоны сильнее влияет на дебит, чем увеличение проницаемости в этой зоне r c r 1 r 2 k 1 K 21 2 c 1 1 2 c 2 2 r r ln k k r r ln Q Q
Парамет р r 1 k 1/k 2 м 0, 1 0, 5 2 10 0, 25 45, 48282 72, 30703 81, 29693 84, 08472 Q/Q 2*100% 0, 5 34, 56898 68, 48764 83, 92812 89, 29662 1 27, 87921 65, 0515 86, 73533 95, 19732 20 15, 18164 53, 45944 101, 3925 133, 2534 Ухудшение проницаемости призабойной зоны сильнее влияет на дебит, чем увеличение проницаемости в этой зоне r c r 1 r 2 k 1 K 21 2 c 1 1 2 c 2 2 r r ln k k r r ln Q Q
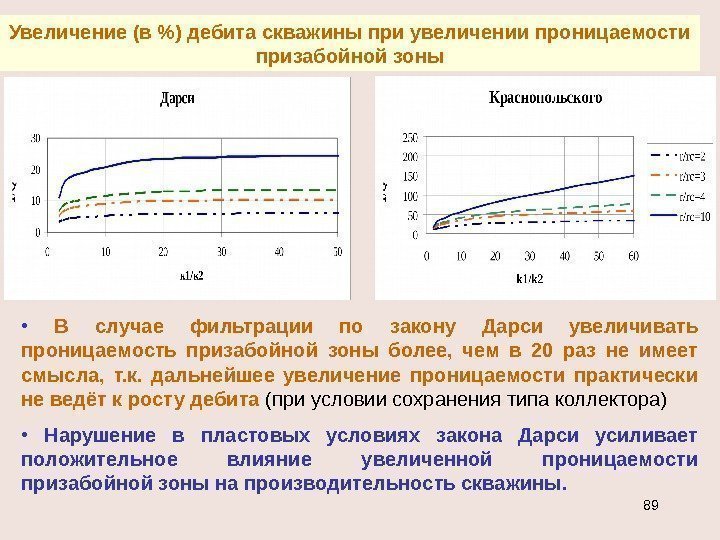
 Увеличение (в %) дебита скважины при увеличении проницаемости призабойной зоны • В случае фильтрации по закону Дарси увеличивать проницаемость призабойной зоны более, чем в 20 раз не имеет смысла, т. к. дальнейшее увеличение проницаемости практически не ведёт к росту дебита (при условии сохранения типа коллектора) • Нарушение в пластовых условиях закона Дарси усиливает положительное влияние увеличенной проницаемости призабойной зоны на производительность скважины.
Увеличение (в %) дебита скважины при увеличении проницаемости призабойной зоны • В случае фильтрации по закону Дарси увеличивать проницаемость призабойной зоны более, чем в 20 раз не имеет смысла, т. к. дальнейшее увеличение проницаемости практически не ведёт к росту дебита (при условии сохранения типа коллектора) • Нарушение в пластовых условиях закона Дарси усиливает положительное влияние увеличенной проницаемости призабойной зоны на производительность скважины.
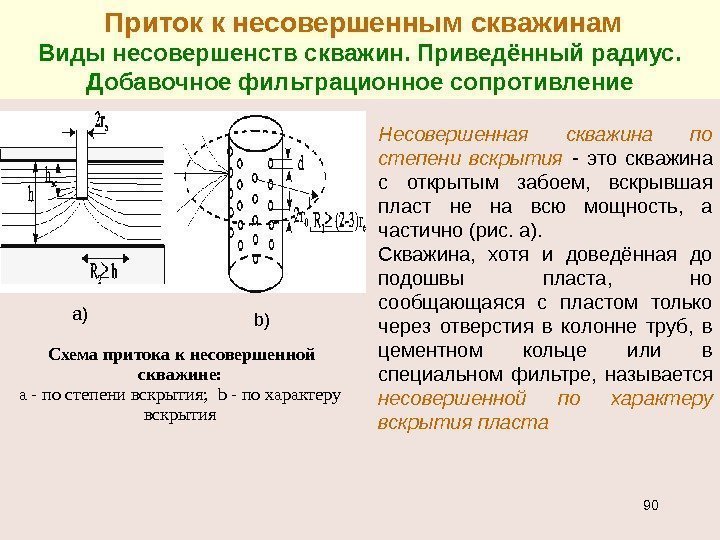
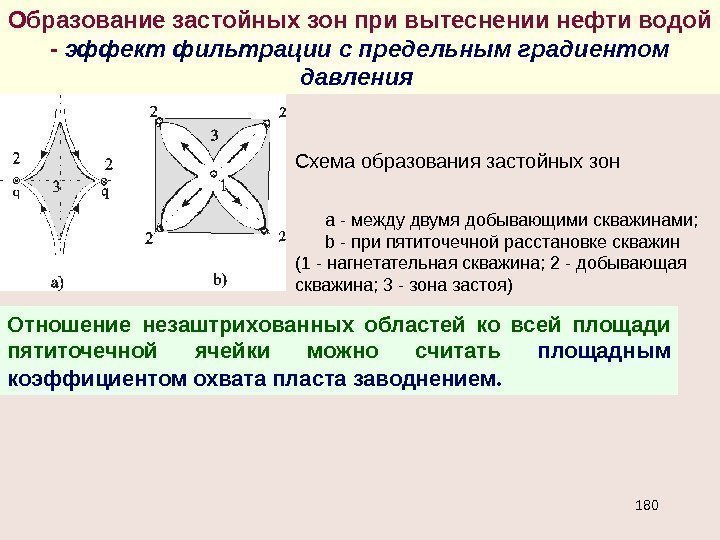
 Схема притока к несовершенной скважине: а — по степени вскрытия; b — по характеру вскрытия Приток к несовершенным скважинам Виды несовершенств скважин. Приведённый радиус. Добавочное фильтрационное сопротивление Несовершенная скважина по степени вскрытия — это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а частично (рис. а). Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта a) b)
Схема притока к несовершенной скважине: а — по степени вскрытия; b — по характеру вскрытия Приток к несовершенным скважинам Виды несовершенств скважин. Приведённый радиус. Добавочное фильтрационное сопротивление Несовершенная скважина по степени вскрытия — это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а частично (рис. а). Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта a) b)
 Параметр несовершенства с. G G Параметр несовершенства зависит от: • относительного вскрытия пласта , где h вс – вскрытая часть пласта , h — толщина пласта; • плотности перфорации (числа отверстий, приходящихся на 1 м фильтра); • размеров и формы отверстий; • глубины прострела. h h h вс Приведенный радиус несовершенной скважины C cпрerr С – коэффициент несовершенства –добавочное фильтрационное сопротивление Приведенный радиус — это радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации.
Параметр несовершенства с. G G Параметр несовершенства зависит от: • относительного вскрытия пласта , где h вс – вскрытая часть пласта , h — толщина пласта; • плотности перфорации (числа отверстий, приходящихся на 1 м фильтра); • размеров и формы отверстий; • глубины прострела. h h h вс Приведенный радиус несовершенной скважины C cпрerr С – коэффициент несовершенства –добавочное фильтрационное сопротивление Приведенный радиус — это радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации.
 Экспериментальные и теоретические исследования притока жидкости к гидродинамически несовершенной скважине Течение по закону Дарси Несовершенство по характеру вскрытия : В. И. Щуров С = С ( a, h) ( a = h / D , h — мощность пласта, D — диаметр скважины; h = h вс / h, h вс — толщина вскрытия ) . Несовершенство по степени вскрытия : И. М. Доуэлл, Маскет, Р. А. Ховард и М. С. Ватсон С = С (плотности перфорации, глубины прострела ) П лотность перфорации — число отверстий на 1 метр Дебит значительно зависит от плотности перфорации только до значений 16 -20 отверстий на 1 метр
Экспериментальные и теоретические исследования притока жидкости к гидродинамически несовершенной скважине Течение по закону Дарси Несовершенство по характеру вскрытия : В. И. Щуров С = С ( a, h) ( a = h / D , h — мощность пласта, D — диаметр скважины; h = h вс / h, h вс — толщина вскрытия ) . Несовершенство по степени вскрытия : И. М. Доуэлл, Маскет, Р. А. Ховард и М. С. Ватсон С = С (плотности перфорации, глубины прострела ) П лотность перфорации — число отверстий на 1 метр Дебит значительно зависит от плотности перфорации только до значений 16 -20 отверстий на 1 метр
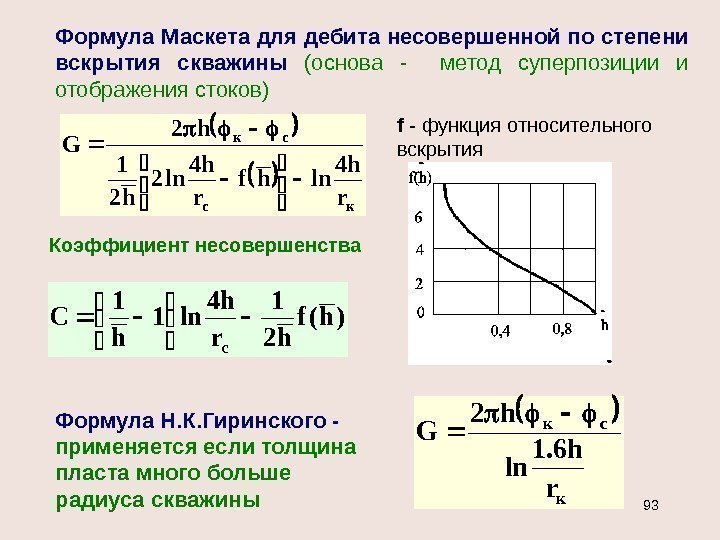
 Формула Маскета для дебита несовершенной по степени вскрытия скважины (основа — метод суперпозиции и отображения стоков) кc ск r h 4 lnhf r h 4 ln 2 h 2 1 h 2 G f — функция относительного вскрытия Формула Н. К. Гиринского — применяется если толщина пласта много больше радиуса скважины к ск r h 6. 1 ln h 2 G )h(f h 2 1 r h 4 ln 1 h 1 С c Коэффициент несовершенства
Формула Маскета для дебита несовершенной по степени вскрытия скважины (основа — метод суперпозиции и отображения стоков) кc ск r h 4 lnhf r h 4 ln 2 h 2 1 h 2 G f — функция относительного вскрытия Формула Н. К. Гиринского — применяется если толщина пласта много больше радиуса скважины к ск r h 6. 1 ln h 2 G )h(f h 2 1 r h 4 ln 1 h 1 С c Коэффициент несовершенства
 Если скважины несовершенны по характеру вскрытия, то коэффициент С увеличивается на величину сопротивления фильтраh. Dn 120 C D — диаметр фильтрового отверстия в см; n — число отверстий на 1 м перфорированной части.
Если скважины несовершенны по характеру вскрытия, то коэффициент С увеличивается на величину сопротивления фильтраh. Dn 120 C D — диаметр фильтрового отверстия в см; n — число отверстий на 1 м перфорированной части.
 Приток реального газа по двухчленному закону к несовершенной скважине Уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине 2 cтcт 2 с 2 к. BQАQрр krh pz B r R kh pz А c cтcт c кcт 22 2 ~ = ; ln ~~ Приток к несовершенной скважине учитывается. введением приведён-ного радиуса скважины в формулу дебита )CC( ccerr Уравнение притока реального газа по закону Дарси к совершенной скважине cт 2 2 2 к. AQрр
Приток реального газа по двухчленному закону к несовершенной скважине Уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине 2 cтcт 2 с 2 к. BQАQрр krh pz B r R kh pz А c cтcт c кcт 22 2 ~ = ; ln ~~ Приток к несовершенной скважине учитывается. введением приведён-ного радиуса скважины в формулу дебита )CC( ccerr Уравнение притока реального газа по закону Дарси к совершенной скважине cт 2 2 2 к. AQрр
 1) R 1 (2 -3) r c — из-за больших скоростей вблизи перфорации происходит нарушение закона Дарси и проявляется в основном несовершенство по характеру вскрытия; закон фильтрации — двухчленный ; 2 cт1 cт1 2 2 QBQАрр 11 2 ~ = ); (ln ~~ 4 1221 31 1 C Rr kh pz B C r. R kh pz А cc тc т cc т С 3 — по графикам Щурова, а С 4 по формуле 2 02 2 4 RN 3 h С N — суммарное число отверстий; R 0 — глубина проникновения перфорационной пули в пласт.
1) R 1 (2 -3) r c — из-за больших скоростей вблизи перфорации происходит нарушение закона Дарси и проявляется в основном несовершенство по характеру вскрытия; закон фильтрации — двухчленный ; 2 cт1 cт1 2 2 QBQАрр 11 2 ~ = ); (ln ~~ 4 1221 31 1 C Rr kh pz B C r. R kh pz А cc тc т cc т С 3 — по графикам Щурова, а С 4 по формуле 2 02 2 4 RN 3 h С N — суммарное число отверстий; R 0 — глубина проникновения перфорационной пули в пласт.
 2) R 2 h — линии тока искривляются из-за несовершенства по степени вскрытия; . фильтрация плоскорадиальна, но с переменной толщиной (от h вск до h ); закон фильтрации — двухчленный. 3) R 2 < r < R к — действует закон Дарси и течение плоскорадиально 2 cт1 cт1 2 2 QBQАрр. ; 1 11 ; ln 1 ; 11 2 ~ = ); (ln ~ 22 11 2 212211 1 2 1 hh =h hh. C R h h h. C C RR kh pz BC RR kh pz А всc тc тc т cт 2 2 2 к. AQрр
2) R 2 h — линии тока искривляются из-за несовершенства по степени вскрытия; . фильтрация плоскорадиальна, но с переменной толщиной (от h вск до h ); закон фильтрации — двухчленный. 3) R 2 < r < R к — действует закон Дарси и течение плоскорадиально 2 cт1 cт1 2 2 QBQАрр. ; 1 11 ; ln 1 ; 11 2 ~ = ); (ln ~ 22 11 2 212211 1 2 1 hh =h hh. C R h h h. C C RR kh pz BC RR kh pz А всc тc тc т cт 2 2 2 к. AQрр
 Общее уравнение притока к несовершенной скважине 2 cтнcтн 2 с 2 к. QВQАрр . 1 2 ~ = ); (ln ~ 422231 1 2 r. CCr krh pz BСC R R kh pz Аc c cтcт н
Общее уравнение притока к несовершенной скважине 2 cтнcтн 2 с 2 к. QВQАрр . 1 2 ~ = ); (ln ~ 422231 1 2 r. CCr krh pz BСC R R kh pz Аc c cтcт н
 Влияние радиуса скважины на её производительность Одиночная скважина r с — радиус 1 -ой скважины, r c / = xr c — радиус 2 -ой скважины; G — дебит 1 -ой скважины, G / =у G — дебит 2 -ой скважины; Закон. Тип потока фильтрацииплоскорадиальныйрадиально-сферический Дарси xln r R ln y c к у=х Краснопольскогоху3 ху ; rr j 1 AG j 1 c j 1 к cк , r r ln h 2 G cк ск
Влияние радиуса скважины на её производительность Одиночная скважина r с — радиус 1 -ой скважины, r c / = xr c — радиус 2 -ой скважины; G — дебит 1 -ой скважины, G / =у G — дебит 2 -ой скважины; Закон. Тип потока фильтрацииплоскорадиальныйрадиально-сферический Дарси xln r R ln y c к у=х Краснопольскогоху3 ху ; rr j 1 AG j 1 c j 1 к cк , r r ln h 2 G cк ск
 НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ УПРУГОЙ ЖИДКОСТИ Упругий режим — основная форма пластовой энергии — энергия упругой деформации жидкостей и материала пласта. Упруговодонапорный — приток жидкости поддерживается за счет напора воды, поступающей извне. Замкнуто-упругий — залежи нефти ограничены либо зонами выклинивания, либо экранами. Жестко-водонапорный режим — вытеснение жидкости из пласта происходит не под действием преобладающего влияния упругости пласта и жидкости (упругие свойства проявляются мало)
НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ УПРУГОЙ ЖИДКОСТИ Упругий режим — основная форма пластовой энергии — энергия упругой деформации жидкостей и материала пласта. Упруговодонапорный — приток жидкости поддерживается за счет напора воды, поступающей извне. Замкнуто-упругий — залежи нефти ограничены либо зонами выклинивания, либо экранами. Жестко-водонапорный режим — вытеснение жидкости из пласта происходит не под действием преобладающего влияния упругости пласта и жидкости (упругие свойства проявляются мало)
 Особенности упругого режима: Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта k , и тем медленнее, чем больше вязкость жидкости и коэффициенты объёмной упругости жидкости и пласта. Параметры упругого режима Важнейшие параметры упругого режима : коэффициенты объёмной упругости жидкости и пласта. Коэффициент объёмной упругости жидкости ж характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу. dp d 1 ж ж ж ж — объём жидкости; знак минус указывает на то, что объём ж увеличивается с уменьшением давления; ж нефти — (7 -30)10 -10 м 2 /н; ж воды — (2, 7 -5)10 -10 м 2 /н.
Особенности упругого режима: Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта k , и тем медленнее, чем больше вязкость жидкости и коэффициенты объёмной упругости жидкости и пласта. Параметры упругого режима Важнейшие параметры упругого режима : коэффициенты объёмной упругости жидкости и пласта. Коэффициент объёмной упругости жидкости ж характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу. dp d 1 ж ж ж ж — объём жидкости; знак минус указывает на то, что объём ж увеличивается с уменьшением давления; ж нефти — (7 -30)10 -10 м 2 /н; ж воды — (2, 7 -5)10 -10 м 2 /н.
 Коэффициент объёмной упругости пласта dp dm dp d 1 п п c п — объём пласта; m — пористость; С слабо и сильно сцементированных горных пород находится в пределах (0, 3 -2)10 -10 м 2 /н. Упругий запас з — это количество жидкости, высвобождающейся в процессе отбора из некоторой области пласта при снижении пластового давления до заданной величины, если высвобождение происходит за счет объёмного расширения жидкости и уменьшения порового пространства пласта. з = ж 0 ж р + с 0 р= * 0 р. , где 0 ж — объём жидкости, насыщающей элемент объёма пласта 0 при начальном давлении р 0 ; р — изменение давления; * = m ж + с — коэффициент упругоёмкости пласта, показывающий долю объема жидкости от выделенного элемента объема пласта, высвобождающейся из элемента пласта при снижении давления на единицу
Коэффициент объёмной упругости пласта dp dm dp d 1 п п c п — объём пласта; m — пористость; С слабо и сильно сцементированных горных пород находится в пределах (0, 3 -2)10 -10 м 2 /н. Упругий запас з — это количество жидкости, высвобождающейся в процессе отбора из некоторой области пласта при снижении пластового давления до заданной величины, если высвобождение происходит за счет объёмного расширения жидкости и уменьшения порового пространства пласта. з = ж 0 ж р + с 0 р= * 0 р. , где 0 ж — объём жидкости, насыщающей элемент объёма пласта 0 при начальном давлении р 0 ; р — изменение давления; * = m ж + с — коэффициент упругоёмкости пласта, показывающий долю объема жидкости от выделенного элемента объема пласта, высвобождающейся из элемента пласта при снижении давления на единицу
 Коэффициент пьезопроводности пласта — характеризует скорость распространения изменения пластового давления 12 TL æ * k = В коллекторах – 1000 см 2 /с æ 50000 см 2 / c или 0. 1 м 2 /с æ 5 м 2 / c. Параметр Фурье — определяет степень нестационарности процесса 2 cr tæ fo 2 æ ê r t Fo
Коэффициент пьезопроводности пласта — характеризует скорость распространения изменения пластового давления 12 TL æ * k = В коллекторах – 1000 см 2 /с æ 50000 см 2 / c или 0. 1 м 2 /с æ 5 м 2 / c. Параметр Фурье — определяет степень нестационарности процесса 2 cr tæ fo 2 æ ê r t Fo
 Дифференциальное уравнение неустановившейся фильтрации упругой жидкости (уравнение пьезопроводности) Допущения : 1) течение по закону Дарси; 2) жидкость и пласт — упругие, т. е. зависимости плотности и пористости от давления линейны0 ж 0 рр1 0 c 0 ррmm Коэффициент объёмной упругости жидкости dp d 1 ж ж ж Коэффициент объёмной упругости пласта dp dm dp d 1 п п c
Дифференциальное уравнение неустановившейся фильтрации упругой жидкости (уравнение пьезопроводности) Допущения : 1) течение по закону Дарси; 2) жидкость и пласт — упругие, т. е. зависимости плотности и пористости от давления линейны0 ж 0 рр1 0 c 0 ррmm Коэффициент объёмной упругости жидкости dp d 1 ж ж ж Коэффициент объёмной упругости пласта dp dm dp d 1 п п c
 tp tm * 0 t m Cdp k ðæ t p — уравнение пьезопроводности , позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом. * = m ж + с
tp tm * 0 t m Cdp k ðæ t p — уравнение пьезопроводности , позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом. * = m ж + с
 Приток к скважине в пласте неограниченных размеров Вывод основного уравнения упругого режима Пласт — упругий, горизонтальный и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным. Уравнение пьезопроводности в цилиндрических координатахæ 2 2 1 1 p p p r r r t возмущение вызвано мгновенным стоком, существовавшим в момент t = t / Решение æ 2 4 ( , ) r (t -t. A p r t C e t t )
Приток к скважине в пласте неограниченных размеров Вывод основного уравнения упругого режима Пласт — упругий, горизонтальный и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным. Уравнение пьезопроводности в цилиндрических координатахæ 2 2 1 1 p p p r r r t возмущение вызвано мгновенным стоком, существовавшим в момент t = t / Решение æ 2 4 ( , ) r (t -t. A p r t C e t t )
 Найдём значения постоянных. 1) В момент времени t = t / давление в пласте р = р к = const. 2) При r > 0 и при t = t / 1) обращается в неопределённость типа / и определяется по правилу Лопиталя: 1) Из уравнения следует, что С = р к. æ æ 2 2 4 4 1 1 r (t -t t te t t e ) )
Найдём значения постоянных. 1) В момент времени t = t / давление в пласте р = р к = const. 2) При r > 0 и при t = t / 1) обращается в неопределённость типа / и определяется по правилу Лопиталя: 1) Из уравнения следует, что С = р к. æ æ 2 2 4 4 1 1 r (t -t t te t t e ) )
 Для определения коэффициента А воспользуемся соотношением для упругого запаса з = * V п р для случая кольцевого элемента пласта с внутренним радиусом r , толщиной h и шириной dr , а также учтем падение давления р = p 0 — p по d з = * р d V п = После интегрирования в пределах от 0 до получим объём жидкости 3 , выделившейся из всего пласта и, учитывая выражение для , определим коэффициент А : 24 ( , ) ð r (t -t ê A p r t e t t )æ k æ*= 2 *4 2 r (t -t )A h e rdr t t æ
Для определения коэффициента А воспользуемся соотношением для упругого запаса з = * V п р для случая кольцевого элемента пласта с внутренним радиусом r , толщиной h и шириной dr , а также учтем падение давления р = p 0 — p по d з = * р d V п = После интегрирования в пределах от 0 до получим объём жидкости 3 , выделившейся из всего пласта и, учитывая выражение для , определим коэффициент А : 24 ( , ) ð r (t -t ê A p r t e t t )æ k æ*= 2 *4 2 r (t -t )A h e rdr t t æ
 Т. о. изменение давления во времени для скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно Изменение давления во времени для скважины, действовающей непрерывно с постоянным дебитом Q = Q 0 в течение времени dt / / через сток выделяется из пласта объём d з = Qdt /
Т. о. изменение давления во времени для скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно Изменение давления во времени для скважины, действовающей непрерывно с постоянным дебитом Q = Q 0 в течение времени dt / / через сток выделяется из пласта объём d з = Qdt /
 Интегрально-показательная функция tæ 4 r u 2 2 du u e tæ 4 r Ei Свойства интегрально-показательной функции : — Ei (- u ) изменяется от 0 до при изменении аргумента от 0 до ; функция — Ei (- u ) представляется в виде сходящегося ряда . . . 18 u 4 u u 5772, 0 u 1 ln)u(Ei 32 5772, 0 u 1 ln)u(Ei Для малых u
Интегрально-показательная функция tæ 4 r u 2 2 du u e tæ 4 r Ei Свойства интегрально-показательной функции : — Ei (- u ) изменяется от 0 до при изменении аргумента от 0 до ; функция — Ei (- u ) представляется в виде сходящегося ряда . . . 18 u 4 u u 5772, 0 u 1 ln)u(Ei 32 5772, 0 u 1 ln)u(Ei Для малых u
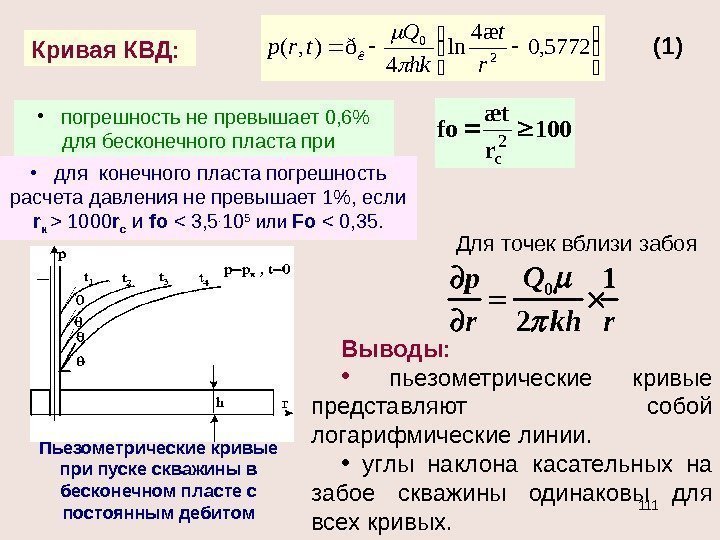
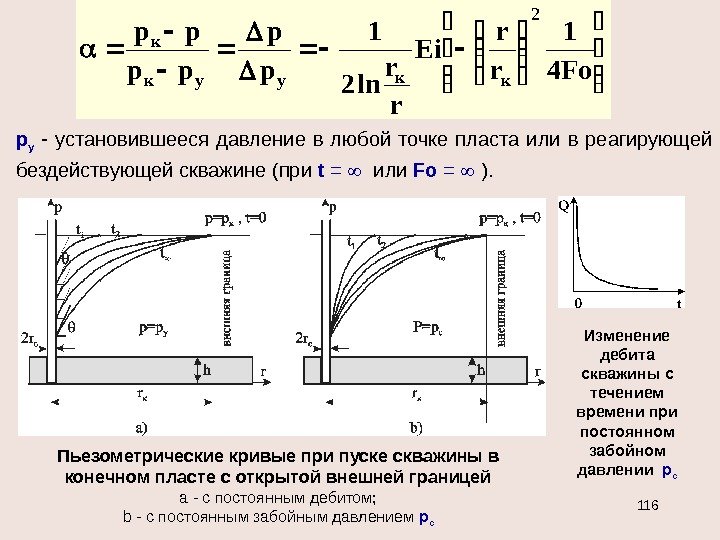
 Кривая КВД: 5772, 0 æ 4 ln 4 ð), (2 0 r t hk Q trpê 100 r tæ fo 2 c • погрешность не превышает 0, 6% для бесконечного пласта при • для конечного пласта погрешность расчета давления не превышает 1%, если r к > 1000 r c и fo < 3, 5. 10 5 или Fo < 0, 35. Пьезометрические кривые при пуске скважины в бесконечном пласте с постоянным дебитом Выводы: • пьезометрические кривые представляют собой логарифмические линии. • углы наклона касательных на забое скважины одинаковы для всех кривых. (1) 0 1 2 Q p r kh r Для точек вблизи забоя
Кривая КВД: 5772, 0 æ 4 ln 4 ð), (2 0 r t hk Q trpê 100 r tæ fo 2 c • погрешность не превышает 0, 6% для бесконечного пласта при • для конечного пласта погрешность расчета давления не превышает 1%, если r к > 1000 r c и fo < 3, 5. 10 5 или Fo < 0, 35. Пьезометрические кривые при пуске скважины в бесконечном пласте с постоянным дебитом Выводы: • пьезометрические кривые представляют собой логарифмические линии. • углы наклона касательных на забое скважины одинаковы для всех кривых. (1) 0 1 2 Q p r kh r Для точек вблизи забоя
 Анализ основной формулы теории упругого режима 1. Основная формула строго справедлива лишь для точечного стока, т. е. при r с =0. Практические расчеты показывают, что ей можно пользоваться даже для укрупнённых скважин ( r с 1 км) и нельзя использовать только в первые доли секунды после пуска скважины. 2. Вскоре после пуска скважины вокруг неё начинает непрерывно увеличиваться область пласта, в которой для каждого момента времени давление распределяется так, как и при установившемся движении, т. е. давление оказывается квазиустановившимся и пьезометрические кривые будут кривыми логарифмического типа. 2 04æ 1 2 r t. Qp e r hk r 3. Стационарная скорость достигается очень быстро на небольших расстояниях от скважины. rh 2 Q u 0 ст 2 0 4 æ 1 2 r t Q u = e h r
Анализ основной формулы теории упругого режима 1. Основная формула строго справедлива лишь для точечного стока, т. е. при r с =0. Практические расчеты показывают, что ей можно пользоваться даже для укрупнённых скважин ( r с 1 км) и нельзя использовать только в первые доли секунды после пуска скважины. 2. Вскоре после пуска скважины вокруг неё начинает непрерывно увеличиваться область пласта, в которой для каждого момента времени давление распределяется так, как и при установившемся движении, т. е. давление оказывается квазиустановившимся и пьезометрические кривые будут кривыми логарифмического типа. 2 04æ 1 2 r t. Qp e r hk r 3. Стационарная скорость достигается очень быстро на небольших расстояниях от скважины. rh 2 Q u 0 ст 2 0 4 æ 1 2 r t Q u = e h r
 Определение коллекторских свойств пласта по данным исследования скважин нестационарными методами Уравнение КВД • гидропроводность пласта → tg 4 Qkh • коэффициент проницаемости пласта → htg 4 Q k • по i = tg и радиусу r c скважины из коэффициента А можно определить коэффициент пьезопроводности пласта æ. . ; , lnррр hk 4 Q i= r 2462 А=i ti. A 0 2 с скс æ где
Определение коллекторских свойств пласта по данным исследования скважин нестационарными методами Уравнение КВД • гидропроводность пласта → tg 4 Qkh • коэффициент проницаемости пласта → htg 4 Q k • по i = tg и радиусу r c скважины из коэффициента А можно определить коэффициент пьезопроводности пласта æ. . ; , lnррр hk 4 Q i= r 2462 А=i ti. A 0 2 с скс æ где
 Особенности кривой и уравнения КВД: • скважина рассматривается как сток постоянной интенсивности в бесконечном, однородном пласте , и возможна мгновенная остановка притока флюида в скважину; • возможны условия, при которых прямолинейный участок на КВД появляется через значительный промежуток времени, либо даже вообще отсутствует; • на форму КВД сказывается также влияние несовершенства скважины и возможное нарушение закона Дарси у стенок скважины
Особенности кривой и уравнения КВД: • скважина рассматривается как сток постоянной интенсивности в бесконечном, однородном пласте , и возможна мгновенная остановка притока флюида в скважину; • возможны условия, при которых прямолинейный участок на КВД появляется через значительный промежуток времени, либо даже вообще отсутствует; • на форму КВД сказывается также влияние несовершенства скважины и возможное нарушение закона Дарси у стенок скважины
 Приток к скважине в пласте конечных размеров в условиях упруго-водонапорного и замкнуто- упругого режима Приток к скважине в пласте конечных размеров с открытой внешней границей Постановка Пусть пласт имеет внешнюю границу радиусом r к , через которую может поступать вода при истощении упругого запаса. В центре пласта имеется скважина радиусом r с , которая мгновенно запускается в эксплуатацию с постоянным дебитом Q 0. Перед пуском скважины давление в пласте было р к. Исходные уравнения Уравнение упругого режима Формула Дюпюи Решаем совместно и получаем уравнение для определения давления
Приток к скважине в пласте конечных размеров в условиях упруго-водонапорного и замкнуто- упругого режима Приток к скважине в пласте конечных размеров с открытой внешней границей Постановка Пусть пласт имеет внешнюю границу радиусом r к , через которую может поступать вода при истощении упругого запаса. В центре пласта имеется скважина радиусом r с , которая мгновенно запускается в эксплуатацию с постоянным дебитом Q 0. Перед пуском скважины давление в пласте было р к. Исходные уравнения Уравнение упругого режима Формула Дюпюи Решаем совместно и получаем уравнение для определения давления
 Fo 4 1 r r Ei r r ln 2 1 р р рр рр 2 ккуук кр у — установившееся давление в любой точке пласта или в реагирующей бездействующей скважине (при t = или Fo = ). Пьезометрические кривые при пуске скважины в конечном пласте с открытой внешней границей а — с постоянным дебитом; b — с постоянным забойным давлением р с Изменение дебита скважины с течением времени при постоянном забойном давлении р с
Fo 4 1 r r Ei r r ln 2 1 р р рр рр 2 ккуук кр у — установившееся давление в любой точке пласта или в реагирующей бездействующей скважине (при t = или Fo = ). Пьезометрические кривые при пуске скважины в конечном пласте с открытой внешней границей а — с постоянным дебитом; b — с постоянным забойным давлением р с Изменение дебита скважины с течением времени при постоянном забойном давлении р с
 Круглый горизонтальный пласт с закрытой внешней границей Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном дебите Постоянный дебит • С момента достижения возмущения границы пласта смещение во времени пьезометрической кривой для закрытого пласта происходит так, что все точки её опускаются на одно и тоже расстояние , т. е. во всех точках пласта давление падает с одной скоростью.
Круглый горизонтальный пласт с закрытой внешней границей Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном дебите Постоянный дебит • С момента достижения возмущения границы пласта смещение во времени пьезометрической кривой для закрытого пласта происходит так, что все точки её опускаются на одно и тоже расстояние , т. е. во всех точках пласта давление падает с одной скоростью.
 • в условиях упругого режима процесс перераспределения давления, а значит, и процесс взаимодействия скважин развивается постепенно, если же и наблюдается аномально быстрое взаимодействие скважин, то это можно объяснить неоднородностью пластов и их анизотропией • при пуске или остановке скважины давление вначале меняется быстро, а затем темп изменения давления замедляется.
• в условиях упругого режима процесс перераспределения давления, а значит, и процесс взаимодействия скважин развивается постепенно, если же и наблюдается аномально быстрое взаимодействие скважин, то это можно объяснить неоднородностью пластов и их анизотропией • при пуске или остановке скважины давление вначале меняется быстро, а затем темп изменения давления замедляется.
 Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении Изменение дебита Q (кр. 1) скважины и суммарной добычи Q cp (кр. 2) с течением времени t. Постоянное забойное давление
Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении Изменение дебита Q (кр. 1) скважины и суммарной добычи Q cp (кр. 2) с течением времени t. Постоянное забойное давление
 Неустановившееся фильтрация газа в пористой среде Уравнение Лейбензонаст ст рр Ср р2 k 2 ст ст 2 kp p Δp mμ t Исходные соотношения æ / = 0 udiv t m
Неустановившееся фильтрация газа в пористой среде Уравнение Лейбензонаст ст рр Ср р2 k 2 ст ст 2 kp p Δp mμ t Исходные соотношения æ / = 0 udiv t m
 tr Ei hk ðQ trpñòñò ê æ 42ð), ( 2 2æ 25, 2 ln 2 ð), ( r t hk ðQ trp ñòñò ê Пьезометрические кривые при неустановившемся притоке газа к скважине в разные моменты времени (а) и изменение давления с течением времени в фиксированных точках пласта ( b) при малых r 2 /(4 æ t ) Уравнение (1) используется для расчета коллекторских параметров газовых пластов методом обработки КВД. Принцип расчета такой же, что и в случае нефтяных скважин, но для получения линейной зависимости по оси ординат надо откладывать не депрессию, а разность квадратов пластового и забойного давлений изменение давления (1)
tr Ei hk ðQ trpñòñò ê æ 42ð), ( 2 2æ 25, 2 ln 2 ð), ( r t hk ðQ trp ñòñò ê Пьезометрические кривые при неустановившемся притоке газа к скважине в разные моменты времени (а) и изменение давления с течением времени в фиксированных точках пласта ( b) при малых r 2 /(4 æ t ) Уравнение (1) используется для расчета коллекторских параметров газовых пластов методом обработки КВД. Принцип расчета такой же, что и в случае нефтяных скважин, но для получения линейной зависимости по оси ординат надо откладывать не депрессию, а разность квадратов пластового и забойного давлений изменение давления (1)
 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОГО РЕЖИМА Аналитические решения большинства задач теории упругого режима представляются громоздкими формулами в виде бесконечного медленно сходящегося ряда или несобственного интеграла, содержащего специальные функции. В связи с этим были предприняты поиски приближенных эффективных решений задач неустановившейся фильтрации упругой жидкости в упругой пористой среде.
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ УПРУГОГО РЕЖИМА Аналитические решения большинства задач теории упругого режима представляются громоздкими формулами в виде бесконечного медленно сходящегося ряда или несобственного интеграла, содержащего специальные функции. В связи с этим были предприняты поиски приближенных эффективных решений задач неустановившейся фильтрации упругой жидкости в упругой пористой среде.
 Метод последовательной смены стационарных состояний (ПССС) /развит И. А. Чарным/ Метод основан на предположении, что давление в пласте меняется во времени значительно медленнее, чем по координатам. Поэтому производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнение Лапласа, описывающее стационарный процесс. 1. В каждый момент времени весь пласт условно разделяется на две области – возмущенную и невозмущенную. 2. В возмущенной области пласта, начинающейся от стенки скважины, давление распределяется по закону установившегося движения жидкости и внешняя граница этой области служит в данный момент контуром питания. 3. В невозмущенной области пласта давление всюду постоянно и равно начальному контурному давлению. 4. Закон движения подвижной границы, разделяющей возмущенную и невозмущенную области, определяется при помощи уравнения материального баланса и граничных условий. Кривые распределения давления в прямолинейно-параллельном потоке по методу ПССС
Метод последовательной смены стационарных состояний (ПССС) /развит И. А. Чарным/ Метод основан на предположении, что давление в пласте меняется во времени значительно медленнее, чем по координатам. Поэтому производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнение Лапласа, описывающее стационарный процесс. 1. В каждый момент времени весь пласт условно разделяется на две области – возмущенную и невозмущенную. 2. В возмущенной области пласта, начинающейся от стенки скважины, давление распределяется по закону установившегося движения жидкости и внешняя граница этой области служит в данный момент контуром питания. 3. В невозмущенной области пласта давление всюду постоянно и равно начальному контурному давлению. 4. Закон движения подвижной границы, разделяющей возмущенную и невозмущенную области, определяется при помощи уравнения материального баланса и граничных условий. Кривые распределения давления в прямолинейно-параллельном потоке по методу ПССС
 Прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости 1. Приток к галерее, на которой поддерживается постоянный дебит Q. Пусть в момент времени t = 0 в горизонтальном пласте постоянной толщины h и ширины В пущена в эксплуатацию прямолинейная галерея, на которой поддерживается постоянный дебит Q. До пуска галереи давление во всем пласте было одинаковым и равным р к. К моменту времени t после пуска галереи граница возмущенной области распространится на длину l(t) (рис 1). Распределение давления в этой области считается установившимся, т. е. описывается линейной зависимостью: . (1) Рис. 1. Кривые распределения давления в прямолинейно-параллельном потоке по методу ПССС
Прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости 1. Приток к галерее, на которой поддерживается постоянный дебит Q. Пусть в момент времени t = 0 в горизонтальном пласте постоянной толщины h и ширины В пущена в эксплуатацию прямолинейная галерея, на которой поддерживается постоянный дебит Q. До пуска галереи давление во всем пласте было одинаковым и равным р к. К моменту времени t после пуска галереи граница возмущенной области распространится на длину l(t) (рис 1). Распределение давления в этой области считается установившимся, т. е. описывается линейной зависимостью: . (1) Рис. 1. Кривые распределения давления в прямолинейно-параллельном потоке по методу ПССС
 Найдем закон перемещения во времени внешней границы возмущенной области l ( t ). Считаем, что количество добытой продукции за время dt равно изменению упругого запаса жидкости в возмущенной зоне пласта за тот же промежуток времени (2) где объем возмущенной зоны пласта, Согласно закону Дарси , отсюда Соотношение (2) можно переписать в виде или т. к Q = const , то Проинтегрируем полученное соотношение
Найдем закон перемещения во времени внешней границы возмущенной области l ( t ). Считаем, что количество добытой продукции за время dt равно изменению упругого запаса жидкости в возмущенной зоне пласта за тот же промежуток времени (2) где объем возмущенной зоны пласта, Согласно закону Дарси , отсюда Соотношение (2) можно переписать в виде или т. к Q = const , то Проинтегрируем полученное соотношение
 Следовательно, формула для распределения давления в пласте (1) будет иметь вид Погрешность определения давления по сравнению с точной формулой составляет 25% *k
Следовательно, формула для распределения давления в пласте (1) будет иметь вид Погрешность определения давления по сравнению с точной формулой составляет 25% *k
 2. Приток к галерее, на которой поддерживается постоянное забойное давление p r = const В пласте в момент времени t = 0 пущена эксплуатационная галерея с постоянным забойным давлением p r = const. До пуска галереи давление во всем пласте было одинаковым и равным p к. Требуется найти распределение давления, закон перемещения границы возмущенной области l ( t ) и изменение дебита галереи во времени Q ( t ). Используем уравнение упругого режима (1) V(t), p , Q определим как и в предыдущем разделе: . , . Подставляя указанные величины в (1) подучим.
2. Приток к галерее, на которой поддерживается постоянное забойное давление p r = const В пласте в момент времени t = 0 пущена эксплуатационная галерея с постоянным забойным давлением p r = const. До пуска галереи давление во всем пласте было одинаковым и равным p к. Требуется найти распределение давления, закон перемещения границы возмущенной области l ( t ) и изменение дебита галереи во времени Q ( t ). Используем уравнение упругого режима (1) V(t), p , Q определим как и в предыдущем разделе: . , . Подставляя указанные величины в (1) подучим.
 После арифметических преобразований и интегрирования находим закон движения границы возмущенной области Распределение давления в возмущенной зоне пласта определяется соотношением а дебит галереи – соотношением Погрешность расчета дебита галереи по сравнению с расчетами по точной формуле составляет 11%. Следовательно, методом последовательной смены стационарных состояний лучше пользоваться в случае неустановившихся прямолинейно-параллель- ных потоков при заданной постоянной депрессии.
После арифметических преобразований и интегрирования находим закон движения границы возмущенной области Распределение давления в возмущенной зоне пласта определяется соотношением а дебит галереи – соотношением Погрешность расчета дебита галереи по сравнению с расчетами по точной формуле составляет 11%. Следовательно, методом последовательной смены стационарных состояний лучше пользоваться в случае неустановившихся прямолинейно-параллель- ных потоков при заданной постоянной депрессии.
 Плоскорадиальный неустановившийся фильтрационный поток упругой жидкости 1. Приток к скважине, на которой поддерживается постоянный дебит Q. Имеем: неограниченный горизонтальный пласт постоянной толщины h. В момент времени t = 0 пущена добывающая скважина радиу сом r c с постоянным дебитом Q. До пуска скважины давление во всем пла сте было одинаковым и равным p к . В соответствии с методом ПССС принимаем, что через время t после пуска скважины вокруг нее образуется возмущенная область радиусом R ( t ), в которой давление будет распределено по стационарному закону. (3) В остальной части пласта сохраняется начальное пластовое давление p к . Требуется найти закон движения границы возмущенной области R(t).
Плоскорадиальный неустановившийся фильтрационный поток упругой жидкости 1. Приток к скважине, на которой поддерживается постоянный дебит Q. Имеем: неограниченный горизонтальный пласт постоянной толщины h. В момент времени t = 0 пущена добывающая скважина радиу сом r c с постоянным дебитом Q. До пуска скважины давление во всем пла сте было одинаковым и равным p к . В соответствии с методом ПССС принимаем, что через время t после пуска скважины вокруг нее образуется возмущенная область радиусом R ( t ), в которой давление будет распределено по стационарному закону. (3) В остальной части пласта сохраняется начальное пластовое давление p к . Требуется найти закон движения границы возмущенной области R(t).
 Рис. 2. Кривые распределения давления в плоскорадиальном потоке в разные моменты времени по методу ПССС (отбор осуществляется при ус- ловии Q = const ) Кривые распределения давления в разные моменты времени приведены на рис. 2. Дебит скважины, очевидно, будет описываться формулой, аналогичной формуле Дюпюи, . Размеры возмущенной области найдем из уравнения материального баланса . (1) при Средневзвешенное пластовое давление в установившемся плоскорадиальном потоке определяется по формуле p %
Рис. 2. Кривые распределения давления в плоскорадиальном потоке в разные моменты времени по методу ПССС (отбор осуществляется при ус- ловии Q = const ) Кривые распределения давления в разные моменты времени приведены на рис. 2. Дебит скважины, очевидно, будет описываться формулой, аналогичной формуле Дюпюи, . Размеры возмущенной области найдем из уравнения материального баланса . (1) при Средневзвешенное пластовое давление в установившемся плоскорадиальном потоке определяется по формуле p %
 Тогда Подставляя приведенные соотношения в уравнение материального балланса (1) получим и после интегрирования в пределах от 0 до t и от r c до R ( t ) имеем Давление в любой точке пласта в любой момент времени t Депрессия в момент времени t : Относительная погрешность уменьшается с течением времени и составляет, по вычислениям, 10, 6%, если 100; 7, 5%, если fo = 103; 5, 7%, если fo = 104.
Тогда Подставляя приведенные соотношения в уравнение материального балланса (1) получим и после интегрирования в пределах от 0 до t и от r c до R ( t ) имеем Давление в любой точке пласта в любой момент времени t Депрессия в момент времени t : Относительная погрешность уменьшается с течением времени и составляет, по вычислениям, 10, 6%, если 100; 7, 5%, если fo = 103; 5, 7%, если fo = 104.
 2. Приток к скважине, на которой поддерживается постоянное давление p с = const Движения границы возмущенной области в этом случае можно определить по графику (рис. 3). Дебит скважины определяется по формуле Дюпюи при p с = const. Сравнение с результатами точных расчетов показывает, что погрешность определения дебита по методу ПССС составляет около 5%. Рис. 24. 3. Зависимость безразмерного радиуса возмущенной области от безразмерного времени fo при отборе жидкости с постоянным забойным давлением
2. Приток к скважине, на которой поддерживается постоянное давление p с = const Движения границы возмущенной области в этом случае можно определить по графику (рис. 3). Дебит скважины определяется по формуле Дюпюи при p с = const. Сравнение с результатами точных расчетов показывает, что погрешность определения дебита по методу ПССС составляет около 5%. Рис. 24. 3. Зависимость безразмерного радиуса возмущенной области от безразмерного времени fo при отборе жидкости с постоянным забойным давлением
 В случаях линейной и радиальной фильтраций в точке перехода от возмущенной к невозмущенной области градиент давления терпит разрыв, что служит одной из причин расхождения между результатами расчетов по методу ПССС и по точному решению. Распределение давления в области фильтрации, получаемое по методу ПССС, является довольно грубым приближением; гораздо точнее этим методом дается связь между дебитом и депрессией, особенно в случае радиальной фильтрации.
В случаях линейной и радиальной фильтраций в точке перехода от возмущенной к невозмущенной области градиент давления терпит разрыв, что служит одной из причин расхождения между результатами расчетов по методу ПССС и по точному решению. Распределение давления в области фильтрации, получаемое по методу ПССС, является довольно грубым приближением; гораздо точнее этим методом дается связь между дебитом и депрессией, особенно в случае радиальной фильтрации.
 Метод А. М. Пирвердяна В методе А. М. Пирвердяна, как и в методе ПССС, неустановившийся фильтрационный поток в каждый момент времени мысленно разбивается на две области – возмущенную и невозмущенную. Граница между этими областями также определяется из уравнения материального баланса. В отличие от метода ПССС распределение давления в возмущенной области по методу А. М. Пирвердяна задается в виде квадратичной параболы так, чтобы пьезометрическая кривая на границе областей касалась горизонтальной линии, представляющей давление в невозмущенной области. Распределение давления уже не будет стационарным, а градиент давления на границе областей становится равным нулю, что обеспечивает плавное смыкание профиля давления в возмущенной и невозмущенной областях.
Метод А. М. Пирвердяна В методе А. М. Пирвердяна, как и в методе ПССС, неустановившийся фильтрационный поток в каждый момент времени мысленно разбивается на две области – возмущенную и невозмущенную. Граница между этими областями также определяется из уравнения материального баланса. В отличие от метода ПССС распределение давления в возмущенной области по методу А. М. Пирвердяна задается в виде квадратичной параболы так, чтобы пьезометрическая кривая на границе областей касалась горизонтальной линии, представляющей давление в невозмущенной области. Распределение давления уже не будет стационарным, а градиент давления на границе областей становится равным нулю, что обеспечивает плавное смыкание профиля давления в возмущенной и невозмущенной областях.
 Прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости 1. Приток к галерее, на которой поддерживается постоянный дебит Q. Пусть в момент времени t = 0 в горизонтальном пласте постоянной толщины h и ширины В пущена в эксплуатацию прямолинейная галерея, на которой поддерживается постоянный дебит Q. До пуска галереи давление во всем пласте было одинаковым и равным р к. К моменту времени t после пуска граница возмущенной области про- двинется на длину l ( t ) , при этом кривая распределения давления в этой области будет иметь вид параболы ( рис. 4 ). Рис. 4. Кривая распределения давления в прямолинейно-параллельном потоке по методу A. M. Пирвердяна
Прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости 1. Приток к галерее, на которой поддерживается постоянный дебит Q. Пусть в момент времени t = 0 в горизонтальном пласте постоянной толщины h и ширины В пущена в эксплуатацию прямолинейная галерея, на которой поддерживается постоянный дебит Q. До пуска галереи давление во всем пласте было одинаковым и равным р к. К моменту времени t после пуска граница возмущенной области про- двинется на длину l ( t ) , при этом кривая распределения давления в этой области будет иметь вид параболы ( рис. 4 ). Рис. 4. Кривая распределения давления в прямолинейно-параллельном потоке по методу A. M. Пирвердяна
 Уравнение параболы, задающей распределение давления в возмущенной области, определяется равенством . (2) Дебит галереи определяется по закону Дарси Продифференцируем выражение для давления и подставим х=0. В результате Т. о. выражение для дебита примет вид (3)
Уравнение параболы, задающей распределение давления в возмущенной области, определяется равенством . (2) Дебит галереи определяется по закону Дарси Продифференцируем выражение для давления и подставим х=0. В результате Т. о. выражение для дебита примет вид (3)
 Закон движения границы возмущенной области определяется из уравнения материального баланса. (1) при Значение средневзвешенного пластового давления в возмущенной области к моменту времени t определим теперь, используя распределение (2) Тогда изменение давления и используя выражение (3) для дебита имеем Подставим полученные выражения в уравнение материального балланса (1)
Закон движения границы возмущенной области определяется из уравнения материального баланса. (1) при Значение средневзвешенного пластового давления в возмущенной области к моменту времени t определим теперь, используя распределение (2) Тогда изменение давления и используя выражение (3) для дебита имеем Подставим полученные выражения в уравнение материального балланса (1)
 Отсюда и после интегрирования в пределах от 0 до t и от 0 до l —— Формула для распределения давления (2) в возмущенной области пласта принимает вид Расчет депрессии дает погрешность по сравнению с точным решением примерно 9%, т. е. в 2, 5 раза меньше, чем по методу ПССС.
Отсюда и после интегрирования в пределах от 0 до t и от 0 до l —— Формула для распределения давления (2) в возмущенной области пласта принимает вид Расчет депрессии дает погрешность по сравнению с точным решением примерно 9%, т. е. в 2, 5 раза меньше, чем по методу ПССС.
 2. Приток к галерее, на которой поддерживается постоянное забойное давление p r = const В пласте в момент времени t = 0 пущена эксплуатационная галерея с постоянным забойным давлением p r = const. До пуска галереи давление во всем пласте было одинаковым и равным p к. Требуется найти распределение давления, закон перемещения границы возмущенной области l ( t ) и изменение дебита галереи во времени Q ( t )
2. Приток к галерее, на которой поддерживается постоянное забойное давление p r = const В пласте в момент времени t = 0 пущена эксплуатационная галерея с постоянным забойным давлением p r = const. До пуска галереи давление во всем пласте было одинаковым и равным p к. Требуется найти распределение давления, закон перемещения границы возмущенной области l ( t ) и изменение дебита галереи во времени Q ( t )
 Для построения приближенного решения по методу А. М. Пирвердяна используем ту же методику, что и для случая 1. Подставим в уравнение материального баланса (1) выражения для расхода, объема и перепада давления в результате получим дифференциальное уравнение , интегрируя которое получим закон движения границы возмущенной области Подставляя найденный закон движения границы возмущенной области в формулы для распределения давления и дебита, получим для давления в возмущенной области пласта соотношение Погрешность расчета дебита галереи по приближенной формуле по сравнению с точным решением составляет около 2, 5%, т. е. и в этом случае расчет по методу А. М. Пирвердяна более, чем в 2 раза точнее, чем по методу ПССС.
Для построения приближенного решения по методу А. М. Пирвердяна используем ту же методику, что и для случая 1. Подставим в уравнение материального баланса (1) выражения для расхода, объема и перепада давления в результате получим дифференциальное уравнение , интегрируя которое получим закон движения границы возмущенной области Подставляя найденный закон движения границы возмущенной области в формулы для распределения давления и дебита, получим для давления в возмущенной области пласта соотношение Погрешность расчета дебита галереи по приближенной формуле по сравнению с точным решением составляет около 2, 5%, т. е. и в этом случае расчет по методу А. М. Пирвердяна более, чем в 2 раза точнее, чем по методу ПССС.
 4. 3. 3. Метод интегральных соотношений (МИС) предложен Г. И. Баренблатом по аналогии с методами пограничного слоя. Основные предпосылки МИС: Область течения, как в предыдущих методах, делится на возмущенную ( длиной или радиуса ) и невозмущенную. В возмущенной области распределение давления представляется в виде многочлена по степеням координаты с коэффициентами, зависящеми от времени: • для прямолинейно-параллельного потока (1) • для плоскорадиального течения (2)
4. 3. 3. Метод интегральных соотношений (МИС) предложен Г. И. Баренблатом по аналогии с методами пограничного слоя. Основные предпосылки МИС: Область течения, как в предыдущих методах, делится на возмущенную ( длиной или радиуса ) и невозмущенную. В возмущенной области распределение давления представляется в виде многочлена по степеням координаты с коэффициентами, зависящеми от времени: • для прямолинейно-параллельного потока (1) • для плоскорадиального течения (2)
 Здесь число n членов многочлена выбирается в засисимости от желаемой точности решения. Коэффициенты многочлена и закон перемещения границы возмущенной области определяют из внутренних граничных условий (на галереи или скважине), из условия неразрывности течения, условий гладкости кривой давления на границе зоны возмущения, а также из интегрального соотношения, определяющего сохранение материального баланса во всей возмушенной области.
Здесь число n членов многочлена выбирается в засисимости от желаемой точности решения. Коэффициенты многочлена и закон перемещения границы возмущенной области определяют из внутренних граничных условий (на галереи или скважине), из условия неразрывности течения, условий гладкости кривой давления на границе зоны возмущения, а также из интегрального соотношения, определяющего сохранение материального баланса во всей возмушенной области.
 ОСНОВЫ ТЕОРИИ ФИЛЬТРАЦИИ МНОГОФАЗНЫХ СИСТЕМ Углеводородные системы Гомогенные Многофазные Составляющие (компоненты) “размазаны” по пространству и взаимодействуют на моле-кулярном уровне. Изменение физических и химических свойств непрерывно. Составляющие(фазы) — разделены отчетливыми геометрическими границами и взаимодействуют на поверхностях раздела. Изменение физических и химических свойств разрывно.
ОСНОВЫ ТЕОРИИ ФИЛЬТРАЦИИ МНОГОФАЗНЫХ СИСТЕМ Углеводородные системы Гомогенные Многофазные Составляющие (компоненты) “размазаны” по пространству и взаимодействуют на моле-кулярном уровне. Изменение физических и химических свойств непрерывно. Составляющие(фазы) — разделены отчетливыми геометрическими границами и взаимодействуют на поверхностях раздела. Изменение физических и химических свойств разрывно.
 Характеристики многофазной среды Насыщенность Скорость фазы Насыщенностью i порового пространства i –й фазы называется доля объема пор V i , занятая этой фазой в элементарном объеме: п i i V V 1 n 1 i i вектор скорости фильтрации u i фазы определяется как вектор, проекция которого на некоторое направление L равна отношению объемного расхода Q i данной фазы к площадке i , перпендику-лярной к указанному направлению: ii Li Q u
Характеристики многофазной среды Насыщенность Скорость фазы Насыщенностью i порового пространства i –й фазы называется доля объема пор V i , занятая этой фазой в элементарном объеме: п i i V V 1 n 1 i i вектор скорости фильтрации u i фазы определяется как вектор, проекция которого на некоторое направление L равна отношению объемного расхода Q i данной фазы к площадке i , перпендику-лярной к указанному направлению: ii Li Q u
 Допущение: • каждая фаза двигается под действием своего давления Закон фильтрации каждой из фаз: ggradp)(k k uiii i i Зависимость относительных проницаемостей k i от насы-щенности Характерная несимметричная форма кривых относительной проницаемости объясняется тем, что при одной и той же насыщенности более смачивающая фаза занимает преимущественно мелкие поры и относительная проницаемость у неё меньше. Сумма относительных проницаемостей для каждого фиксированного значения 1)(k)(k 21 Присутствие связанной смачивающей фазы мало влияет на течение не смачивающей жидкости, тогда как присутствие остаточной не смачивающей фазы значительно «стесняет» движение смачивающей фазы.
Допущение: • каждая фаза двигается под действием своего давления Закон фильтрации каждой из фаз: ggradp)(k k uiii i i Зависимость относительных проницаемостей k i от насы-щенности Характерная несимметричная форма кривых относительной проницаемости объясняется тем, что при одной и той же насыщенности более смачивающая фаза занимает преимущественно мелкие поры и относительная проницаемость у неё меньше. Сумма относительных проницаемостей для каждого фиксированного значения 1)(k)(k 21 Присутствие связанной смачивающей фазы мало влияет на течение не смачивающей жидкости, тогда как присутствие остаточной не смачивающей фазы значительно «стесняет» движение смачивающей фазы.
 Характер зависимостей определяется различной степенью смачивания твердых зерен породы фазами, причем относительная проницаемость зависит только от водонасыщенности — наиболее проницаемой фазы — воды, и почти не зависит от нефте- и газонасыщенности. Относительная фазовая проницаемость в многофазном потоке почти не зависит от вязкости жидкости, ее плотности, внутрижидкостного натяжения, градиента давления, скорости.
Характер зависимостей определяется различной степенью смачивания твердых зерен породы фазами, причем относительная проницаемость зависит только от водонасыщенности — наиболее проницаемой фазы — воды, и почти не зависит от нефте- и газонасыщенности. Относительная фазовая проницаемость в многофазном потоке почти не зависит от вязкости жидкости, ее плотности, внутрижидкостного натяжения, градиента давления, скорости.
 Капиллярное давление — р к = р 2 -р 1 Большее давление — на стороне жидкости, не смачивающей твердые зерна породы. )(J k m cos)(ррпкк Зависимость функции Леверетта от насыщенности : 1 — кривая вытеснения; 2 — кривая пропитки; А — остаточная насыщенность вытесняемой жидкости п — коэффициент межфазного поверхностного натяжения; — статический краевой угол смачивания между жидкостями и породой; m — пористость; J ( ) — безразмерная функция Леверетта.
Капиллярное давление — р к = р 2 -р 1 Большее давление — на стороне жидкости, не смачивающей твердые зерна породы. )(J k m cos)(ррпкк Зависимость функции Леверетта от насыщенности : 1 — кривая вытеснения; 2 — кривая пропитки; А — остаточная насыщенность вытесняемой жидкости п — коэффициент межфазного поверхностного натяжения; — статический краевой угол смачивания между жидкостями и породой; m — пористость; J ( ) — безразмерная функция Леверетта.
 Процессы многофазной фильтрации зависят от: 1) размеров области течения 2) от характерного времени фильтрационного процесса; Влияние капиллярных сил на распределение давления незначительно и их действие проявляется в локальных процессах перераспределения фаз. Если размеры области малы, то при достаточно малых скоростях фильтрации капиллярные силы могут превзойти внешний перепад давления. Если рассматривается движение в очень большой области (например, в целой нефтяной или газовой залежи), то влияние капиллярных сил на распределение давления незначительно и их действие проявляется в локальных процессах перераспределения фаз.
Процессы многофазной фильтрации зависят от: 1) размеров области течения 2) от характерного времени фильтрационного процесса; Влияние капиллярных сил на распределение давления незначительно и их действие проявляется в локальных процессах перераспределения фаз. Если размеры области малы, то при достаточно малых скоростях фильтрации капиллярные силы могут превзойти внешний перепад давления. Если рассматривается движение в очень большой области (например, в целой нефтяной или газовой залежи), то влияние капиллярных сил на распределение давления незначительно и их действие проявляется в локальных процессах перераспределения фаз.
 Исходные уравнения многофазной фильтрации Уравнения неразрывности 0 udivm t 111 0 udiv 1 m t 222 • Жидкости несжимаемы — нестационарные процессы упругого перераспределения давления заканчиваются в начале процесса вытеснения. • Среда — недеформируема 0 udiv t m 1 0 udiv t m
Исходные уравнения многофазной фильтрации Уравнения неразрывности 0 udivm t 111 0 udiv 1 m t 222 • Жидкости несжимаемы — нестационарные процессы упругого перераспределения давления заканчиваются в начале процесса вытеснения. • Среда — недеформируема 0 udiv t m 1 0 udiv t m
 Уравнения движения для многофазной фильтрации ggradp)(k k u iii ii + Связь между давлениями )(J km cos)(ррр пк 12 Допущение: • в любой точке каждая из фаз находится в состоянии термодинамического равновесия • процессы однонаправленные Тогда: k i = k i ( ) и р к = р к ( ) + замыкающие отношения
Уравнения движения для многофазной фильтрации ggradp)(k k u iii ii + Связь между давлениями )(J km cos)(ррр пк 12 Допущение: • в любой точке каждая из фаз находится в состоянии термодинамического равновесия • процессы однонаправленные Тогда: k i = k i ( ) и р к = р к ( ) + замыкающие отношения
 Потенциальное движение газированной жидкости Газированная жидкость — смесь жидкой и газовой фаз При увеличении содержания свободного газа фазовая проницаемость для газа растет, а фазовая проницаемость для жидкой фазы уменьшается. Необходимое условие – давление меньше давления насыщения Расчеты параметров потока газированной жидкости необходимо проводить на основе многофазной модели течения
Потенциальное движение газированной жидкости Газированная жидкость — смесь жидкой и газовой фаз При увеличении содержания свободного газа фазовая проницаемость для газа растет, а фазовая проницаемость для жидкой фазы уменьшается. Необходимое условие – давление меньше давления насыщения Расчеты параметров потока газированной жидкости необходимо проводить на основе многофазной модели течения
 Массовая скорость фильтрации капельно-жидкой фазы газированной жидкости dr dр )р( Ar G жj ж ж жж ж k Массовая скорость фильтрации свободного газа смеси dr dр )р( Ar G гсj гс гс гс k Массовая скорость фильтрации газа, находящегося в растворе )р( dr dр )р( Ar G мжj гр σ м (р) = G гр / G ж — массовая растворимость газа в жидкости, т. е. количество массы газа, раство-ренного в единице массы жидкости при давлении р
Массовая скорость фильтрации капельно-жидкой фазы газированной жидкости dr dр )р( Ar G жj ж ж жж ж k Массовая скорость фильтрации свободного газа смеси dr dр )р( Ar G гсj гс гс гс k Массовая скорость фильтрации газа, находящегося в растворе )р( dr dр )р( Ar G мжj гр σ м (р) = G гр / G ж — массовая растворимость газа в жидкости, т. е. количество массы газа, раство-ренного в единице массы жидкости при давлении р
 Массовая скорость всего газа ( суммируем последние два соотношения ))р( Ar G dr dр )р( Ar GG Ar G мj ж гj гргс j г Объемный газовый фактор Г представляет собой отношение объемного газового дебита Q г , приведенного к давлению 1 ат , к объемному дебиту жидкого компонента Q ж , приведенному к тем же условиям. Газовый фактор Г в одномерном установившемся потоке сохраняется постоянным вдоль всего потока. )р( )р( Q Q Г ж г 0 г 0 ж ж ж 0 г г г G Q, G Q г 0 и ж 0 — значения плотности газа и жидкого компонента — объемная растворимость газа в жидкости )р()р( м 0 г 0 ж σ(р) = р Закон Генри растворимости газа в жидкости ( р < 10 МПа ) — объемный козффиииент растворимости , постоянный для данных жидкости и газа
Массовая скорость всего газа ( суммируем последние два соотношения ))р( Ar G dr dр )р( Ar GG Ar G мj ж гj гргс j г Объемный газовый фактор Г представляет собой отношение объемного газового дебита Q г , приведенного к давлению 1 ат , к объемному дебиту жидкого компонента Q ж , приведенному к тем же условиям. Газовый фактор Г в одномерном установившемся потоке сохраняется постоянным вдоль всего потока. )р( )р( Q Q Г ж г 0 г 0 ж ж ж 0 г г г G Q, G Q г 0 и ж 0 — значения плотности газа и жидкого компонента — объемная растворимость газа в жидкости )р()р( м 0 г 0 ж σ(р) = р Закон Генри растворимости газа в жидкости ( р < 10 МПа ) — объемный козффиииент растворимости , постоянный для данных жидкости и газа
 Формула газового фактора через физические параметры0 0 ( ) ( ) æ ã ã æ æ ã ð k s ð Ã ð ð k s ð т. к. i ii i k Объемный коэффициент нефти (р) характеризует изменение объема нефти вследствие изменений давления и количества растворенного газа. Величина (р) есть отношение удельных объемов нефти в пластовых и атмосферных условиях )р( ж 0 ж )р( )р( Q Q Г ж г 0 г 0 ж ж г
Формула газового фактора через физические параметры0 0 ( ) ( ) æ ã ã æ æ ã ð k s ð Ã ð ð k s ð т. к. i ii i k Объемный коэффициент нефти (р) характеризует изменение объема нефти вследствие изменений давления и количества растворенного газа. Величина (р) есть отношение удельных объемов нефти в пластовых и атмосферных условиях )р( ж 0 ж )р( )р( Q Q Г ж г 0 г 0 ж ж г
 Формула газового фактора через объёмный коэффициент где При постоянном газовом факторе Г данное уравнение, выражая зависимость между давлением р и насыщенностью s , служит уравнением состояния газированной жидкости Функции μ ж (р), μ г ( p ), (р) и σ(р) определяются по экспериментальным данным. Кривые зависимости коэффициента растворимости газа в нефти и объёмного коэффициента нефти от давления (1)
Формула газового фактора через объёмный коэффициент где При постоянном газовом факторе Г данное уравнение, выражая зависимость между давлением р и насыщенностью s , служит уравнением состояния газированной жидкости Функции μ ж (р), μ г ( p ), (р) и σ(р) определяются по экспериментальным данным. Кривые зависимости коэффициента растворимости газа в нефти и объёмного коэффициента нефти от давления (1)
 2. Определяем потенциальную функцию Определение массового дебита жидкой фазы газированной нефти 1. Находим насыщенность s из (1) Cdp ð ðpsk ð æ ææ )( )( 4. Подставляя граничные значения (р) в уравнение получаем формулу массового дебита жидкой фазы ln 2 c ê ñê rrh. G ñ ñæññ ê êæêê c ê skðskð r r hk G )()( ln)1( 2** ε — показатель «несовершенства» жидкости 0 <ε < 1 – для газированной жидкости
2. Определяем потенциальную функцию Определение массового дебита жидкой фазы газированной нефти 1. Находим насыщенность s из (1) Cdp ð ðpsk ð æ ææ )( )( 4. Подставляя граничные значения (р) в уравнение получаем формулу массового дебита жидкой фазы ln 2 c ê ñê rrh. G ñ ñæññ ê êæêê c ê skðskð r r hk G )()( ln)1( 2** ε — показатель «несовершенства» жидкости 0 <ε < 1 – для газированной жидкости
 Вывод зависимости для объемного дебита жидкой фазы газированной смеси в плоско-радиальном потоке в виде формулы Дюпюи Допущения: k , ж и μ ж — постоянны 1. Получим выражения для потенциалов на забое и контуре. С)р(Ф k , С)р(Ф k с ж ж ск ж ж к dp)p(sk)р(Ф * ж 2. Вычитаем почленно полученные выражения и применяем теорему о среднем )рр( k dp)p(kdp)p(sk k ск ж / жж р р ж ж ж р р * ж ж ж ск к с 3. Подставим Δ в и разделив на ж находим: c к ск r r ln h 2 G c к ж ск / ж r r ln )рр(hk 2 Q k ‘ f ж – некоторое среднее значение функции k f (р) в интервале изменения р от р с до р к.
Вывод зависимости для объемного дебита жидкой фазы газированной смеси в плоско-радиальном потоке в виде формулы Дюпюи Допущения: k , ж и μ ж — постоянны 1. Получим выражения для потенциалов на забое и контуре. С)р(Ф k , С)р(Ф k с ж ж ск ж ж к dp)p(sk)р(Ф * ж 2. Вычитаем почленно полученные выражения и применяем теорему о среднем )рр( k dp)p(kdp)p(sk k ск ж / жж р р ж ж ж р р * ж ж ж ск к с 3. Подставим Δ в и разделив на ж находим: c к ск r r ln h 2 G c к ж ск / ж r r ln )рр(hk 2 Q k ‘ f ж – некоторое среднее значение функции k f (р) в интервале изменения р от р с до р к.
 При практических расчетах используют зависимости для дебита предложенные: • Вогелем , где V c =0, 8 • Фетковичем Коэффициент С можно интерпретировать как индекс продуктивности пласта, а его значение зависит от подвижности фаз Значение коэффициента С увеличивается с ростом k и h и уменьшается с ростом скина 2 max 21 1 c c ê ê p p Q Q V V p p
При практических расчетах используют зависимости для дебита предложенные: • Вогелем , где V c =0, 8 • Фетковичем Коэффициент С можно интерпретировать как индекс продуктивности пласта, а его значение зависит от подвижности фаз Значение коэффициента С увеличивается с ростом k и h и уменьшается с ростом скина 2 max 21 1 c c ê ê p p Q Q V V p p
 Резюме: дебит газированной жидкости равен дебиту воображаемой однородной несжимаемой жидкости , движущейся в пласте с коэффициентом проницаемости k ‘ ж , меньшим k. Отличие от классической формулы Дюпюи Для газированной жидкости дебит зависит не только от депрессии р с , но и от величины давления р к или р с. Приближенные выражения для k ‘ ж : 1. И. А. Чарный — k ‘ ж = 0, 65 k — для несцементированных песков 2. М. М. Глоговский и М. Д. Розенберг k 43, 21944, 0 k ж г/ ж 1 к близко s р р 0, 2 к к с, 1; 005, 0015, 0 ж г c к ж ск / ж r r ln )рр(hk 2 Q
Резюме: дебит газированной жидкости равен дебиту воображаемой однородной несжимаемой жидкости , движущейся в пласте с коэффициентом проницаемости k ‘ ж , меньшим k. Отличие от классической формулы Дюпюи Для газированной жидкости дебит зависит не только от депрессии р с , но и от величины давления р к или р с. Приближенные выражения для k ‘ ж : 1. И. А. Чарный — k ‘ ж = 0, 65 k — для несцементированных песков 2. М. М. Глоговский и М. Д. Розенберг k 43, 21944, 0 k ж г/ ж 1 к близко s р р 0, 2 к к с, 1; 005, 0015, 0 ж г c к ж ск / ж r r ln )рр(hk 2 Q
 ВЫВОДЫ по течению газированной жидкости 1. Дебит газированной жидкости прочих равных условиях всегда меньше дебита однородной несжимаемой жидкости. 2. С повышением газового фактора при неизменяющейся депрессии р с дебит жидкой фазы уменьшается, а дебит газа увеличивается 3. При данной депрессии р с и газовом факторе Г более высокий дебит будет при более высоком пластовом давлении. 4. Для повышения добычи более эффективным средством является увеличение депрессии за счет повышения пластового (контурного) давления р к , но не путем снижения забойного давления р с .
ВЫВОДЫ по течению газированной жидкости 1. Дебит газированной жидкости прочих равных условиях всегда меньше дебита однородной несжимаемой жидкости. 2. С повышением газового фактора при неизменяющейся депрессии р с дебит жидкой фазы уменьшается, а дебит газа увеличивается 3. При данной депрессии р с и газовом факторе Г более высокий дебит будет при более высоком пластовом давлении. 4. Для повышения добычи более эффективным средством является увеличение депрессии за счет повышения пластового (контурного) давления р к , но не путем снижения забойного давления р с .
 5. Зависимость дебита жидкости и газа от депрессии, в отличие от однородной жидкости, не является линейной. 6. Искривление индикаторной линии при фильтрации газированной жидкости еще не означает наличия отклонений от линейного закона фильтрации. 7. Индикаторная кривая для реальной газированной нефти имеет меньший наклон, чем кривая для идеальной газированной жидкости, т. е. для реальной жидкости существуют добавочные сопротивления при фильтрации, не учтенные в идеальной жидкости.
5. Зависимость дебита жидкости и газа от депрессии, в отличие от однородной жидкости, не является линейной. 6. Искривление индикаторной линии при фильтрации газированной жидкости еще не означает наличия отклонений от линейного закона фильтрации. 7. Индикаторная кривая для реальной газированной нефти имеет меньший наклон, чем кривая для идеальной газированной жидкости, т. е. для реальной жидкости существуют добавочные сопротивления при фильтрации, не учтенные в идеальной жидкости.
 8. Начальный период (первые месяцы) неустановившейся радиальной фильтрации газированной жидкости в условиях режима растворенного газа характеризуется высокими дебитами жидкости и газа. 9. Величина дебита жидкости быстро уменьшается с течением времени, но стремится к асимптоте относительно стабильной добычи. При этом абсолютная величина дебита жидкости невелика (уменьшается на порядок). 10. Темп падения дебита газа меньше, чем темп падения дебита жидкости. 11. Газовый фактор сначала резко возрастает, достигая в скором времени максимума, затем постепенно уменьшается.
8. Начальный период (первые месяцы) неустановившейся радиальной фильтрации газированной жидкости в условиях режима растворенного газа характеризуется высокими дебитами жидкости и газа. 9. Величина дебита жидкости быстро уменьшается с течением времени, но стремится к асимптоте относительно стабильной добычи. При этом абсолютная величина дебита жидкости невелика (уменьшается на порядок). 10. Темп падения дебита газа меньше, чем темп падения дебита жидкости. 11. Газовый фактор сначала резко возрастает, достигая в скором времени максимума, затем постепенно уменьшается.
 • жидкости предполагаются несмешивающимися (взаимно нерастворимыми); • жидкости считаются несжимаемыми, а пористая среда — недеформируемой; • фазовые переходы отсутствуют; • коэффициенты вязкости фаз постоянны; • относительные фазовые проницаемости и капиллярное давление являются известными однозначными функциями насыщенности; • гистерезисные явления не учитываются (рассматриваются только однонаправленные процессы). Одномерные модели вытеснения несмешивающихся жидкостей Основные допущения :
• жидкости предполагаются несмешивающимися (взаимно нерастворимыми); • жидкости считаются несжимаемыми, а пористая среда — недеформируемой; • фазовые переходы отсутствуют; • коэффициенты вязкости фаз постоянны; • относительные фазовые проницаемости и капиллярное давление являются известными однозначными функциями насыщенности; • гистерезисные явления не учитываются (рассматриваются только однонаправленные процессы). Одномерные модели вытеснения несмешивающихся жидкостей Основные допущения :
 Характерной особенностью данной системы является то, что её можно свести к одному уравнению для насыщенности. Полная система уравнений х u t m 1 х u t m 2 sing x p )(k k u 1 1 1 sing x p )(k k u 2 2 2 Схема одномерной двухфазной фильтрации с учетом силы тяжести d dp р fg x pk t k x f tu t m к к к / ‘ 2 2 0)(sin)( )( )( u = u 1 + u 2 ; = 2 — 1 ; )(k)(k )(f 201 1 функция Баклея Леверетта или функция распределения потоков фаз
Характерной особенностью данной системы является то, что её можно свести к одному уравнению для насыщенности. Полная система уравнений х u t m 1 х u t m 2 sing x p )(k k u 1 1 1 sing x p )(k k u 2 2 2 Схема одномерной двухфазной фильтрации с учетом силы тяжести d dp р fg x pk t k x f tu t m к к к / ‘ 2 2 0)(sin)( )( )( u = u 1 + u 2 ; = 2 — 1 ; )(k)(k )(f 201 1 функция Баклея Леверетта или функция распределения потоков фаз
 Граничные условия: на входе в пласт (нагнетательная скважина или галерея): расход закачиваемой воды равенство нулю скорости фильтрации нефти из последнего условия вытекает , что k 2 = 0 , следовательно, на этой поверхности = *. Начальные условия: задаются значения неизвестной функции в зависимости от пространственных координат при t = 0. Можно считать, что при t = 0 насыщенность всюду постоянна (например, = *).
Граничные условия: на входе в пласт (нагнетательная скважина или галерея): расход закачиваемой воды равенство нулю скорости фильтрации нефти из последнего условия вытекает , что k 2 = 0 , следовательно, на этой поверхности = *. Начальные условия: задаются значения неизвестной функции в зависимости от пространственных координат при t = 0. Можно считать, что при t = 0 насыщенность всюду постоянна (например, = *).
 Граничные условия: На выходе из пласта: пренебрегаем градиентом капиллярного давления по сравнению с градиентом давления в фазах, т. е. считаем, что при x = L , откуда следует, что при x = L. Экспериментально установлено, что вода не вытекает из гидрофильного пласта, а накапливается в выходном сечении, пока её насыщенность не достигнет значения *. В момент достижения значения * вода прорывается из пласта с сохранением на выходе этого значения насыщенности. Это явление получило название концевого эффекта. Математически оно приводится к сложному нелинейному граничному условию на выходе 0 х рк 0 х
Граничные условия: На выходе из пласта: пренебрегаем градиентом капиллярного давления по сравнению с градиентом давления в фазах, т. е. считаем, что при x = L , откуда следует, что при x = L. Экспериментально установлено, что вода не вытекает из гидрофильного пласта, а накапливается в выходном сечении, пока её насыщенность не достигнет значения *. В момент достижения значения * вода прорывается из пласта с сохранением на выходе этого значения насыщенности. Это явление получило название концевого эффекта. Математически оно приводится к сложному нелинейному граничному условию на выходе 0 х рк 0 х
 Модель Рапопорта Лиса — для вытеснения без учета силы тяжести. Дифференциальное уравнение для насыщенности в данной модели – параболического типа. Модель Баклея Леверетта — для вытеснения без учета капиллярных сил. Уравнение насыщенности задач данного типа принадлежит к классу квазилинейных гиперболических уравнений первого порядка.
Модель Рапопорта Лиса — для вытеснения без учета силы тяжести. Дифференциальное уравнение для насыщенности в данной модели – параболического типа. Модель Баклея Леверетта — для вытеснения без учета капиллярных сил. Уравнение насыщенности задач данного типа принадлежит к классу квазилинейных гиперболических уравнений первого порядка.
 Функция Баклея Леверетта или функция распределения потоков фаз f ( ) равна отношению скорости фильтрации вытесняющей фазы к суммарной скорости и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз определяет полноту вытеснения и характер распределения газоконденсатонефтенасы-щенности по пласту Вид функции Баклея-Леверетта и её производной Задачи повышения нефте- и газоконденсатоотдачи сводятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции f ( ) в направлении увеличения полноты вытеснения Задача Баклея Леверетта и ее обобщения
Функция Баклея Леверетта или функция распределения потоков фаз f ( ) равна отношению скорости фильтрации вытесняющей фазы к суммарной скорости и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз определяет полноту вытеснения и характер распределения газоконденсатонефтенасы-щенности по пласту Вид функции Баклея-Леверетта и её производной Задачи повышения нефте- и газоконденсатоотдачи сводятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции f ( ) в направлении увеличения полноты вытеснения Задача Баклея Леверетта и ее обобщения
 Устранение многозначности распределения насыщенности введением скачка. Дисперсия волн — зависимость скорости распространения того или иного значения насыщенности от величины этой насыщенности. Графики функции Баклея — Леверетта (а) и её производной ( b ) для различных отношений вязкости 0 = 1 / 2 С ростом отношения вязкостей кривая f ( ) сдвигается вправо и эффективность вытеснения возрастает. При 0 п большие насыщенности распространяются с большими скоростями, а при п 1 скорость распространения постоянного значения насыщенности начинает уменьшаться.
Устранение многозначности распределения насыщенности введением скачка. Дисперсия волн — зависимость скорости распространения того или иного значения насыщенности от величины этой насыщенности. Графики функции Баклея — Леверетта (а) и её производной ( b ) для различных отношений вязкости 0 = 1 / 2 С ростом отношения вязкостей кривая f ( ) сдвигается вправо и эффективность вытеснения возрастает. При 0 п большие насыщенности распространяются с большими скоростями, а при п 1 скорость распространения постоянного значения насыщенности начинает уменьшаться.
 Задача Рапопорта – Лиса Распределение насыщенности в стабилизированной зоне l Cтабилизированная зона насыщенности перемещается, не изменяя своей формы, и распределение насыщенности в ней при постоянной скорости вытеснения – стационарно.
Задача Рапопорта – Лиса Распределение насыщенности в стабилизированной зоне l Cтабилизированная зона насыщенности перемещается, не изменяя своей формы, и распределение насыщенности в ней при постоянной скорости вытеснения – стационарно.
 ОСНОВЫ ФИЛЬТРАЦИИ НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ Рассматриваем нелинейные законы фильтрации, описывающие только безинерционные движения при условии, что фильтрующиеся жидкости обладают неньютоновскими свойствами.
ОСНОВЫ ФИЛЬТРАЦИИ НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ Рассматриваем нелинейные законы фильтрации, описывающие только безинерционные движения при условии, что фильтрующиеся жидкости обладают неньютоновскими свойствами.
 Реологические модели фильтрующихся жидкостейdy du Ньютоновские жидкости dy du f Стационарно реологические жидкости t, dy du f Нестационарно реологические жидкости dt d , dy du f Вязкоупругие жидкости — среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений.
Реологические модели фильтрующихся жидкостейdy du Ньютоновские жидкости dy du f Стационарно реологические жидкости t, dy du f Нестационарно реологические жидкости dt d , dy du f Вязкоупругие жидкости — среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений.
 Стационарно реологические жидкости 0 1 dy du 0 dy du при > 0 , при 0. Вязкопластичные жидкости 0 — начальное (предельное) напряжение сдвига n dy du k a) n 1 Дилатантные жидкости dy du * кажущаяся вязкость 1 n * dy du k * убывает с возрастанием градиента скорости. * увеличивается с возрастанием градиента скорости. кр. 1 кр. 3 кр. 4 Дилатантная — суспензии с большим содержанием твердой фазы. Псевдопластичная — растворы и расплавы полимеров
Стационарно реологические жидкости 0 1 dy du 0 dy du при > 0 , при 0. Вязкопластичные жидкости 0 — начальное (предельное) напряжение сдвига n dy du k a) n 1 Дилатантные жидкости dy du * кажущаяся вязкость 1 n * dy du k * убывает с возрастанием градиента скорости. * увеличивается с возрастанием градиента скорости. кр. 1 кр. 3 кр. 4 Дилатантная — суспензии с большим содержанием твердой фазы. Псевдопластичная — растворы и расплавы полимеров
 ЗАКОНЫ ФИЛЬТРАЦИИ Вязкопластичная жидкость в пористой среде u u u k gradp — u >0; , u =0, где k ~ 0 предельный (начальный) градиент Индикаторные линии: 1 — линейная аппроксимация неньютоновской жидкости; 2 — реальная неньютоновская жидкость; 3 – ньютоновская по закону Дарси Неньютоновские эффекты проявляются при малых скоростях фильтрации и в средах с малым размером пор, т. е. с малой проницаемостью Из-за неньютоновских свойств нефтей пропластки последовательно включаются в работу по мере превышения градиента давления предельного градиента сдвига.
ЗАКОНЫ ФИЛЬТРАЦИИ Вязкопластичная жидкость в пористой среде u u u k gradp — u >0; , u =0, где k ~ 0 предельный (начальный) градиент Индикаторные линии: 1 — линейная аппроксимация неньютоновской жидкости; 2 — реальная неньютоновская жидкость; 3 – ньютоновская по закону Дарси Неньютоновские эффекты проявляются при малых скоростях фильтрации и в средах с малым размером пор, т. е. с малой проницаемостью Из-за неньютоновских свойств нефтей пропластки последовательно включаются в работу по мере превышения градиента давления предельного градиента сдвига.
 Степенной закон фильтрацииgradp. Cu n , где С — экспериментальная константа; n >0. Степенной закон, соответствующий псевдопластичному флюиду, хорошо описывает движение растворов полимеров в пористой среде и используется при расчете “полимерного” заводнения пластов с целью повышения их нефтеотдачи.
Степенной закон фильтрацииgradp. Cu n , где С — экспериментальная константа; n >0. Степенной закон, соответствующий псевдопластичному флюиду, хорошо описывает движение растворов полимеров в пористой среде и используется при расчете “полимерного” заводнения пластов с целью повышения их нефтеотдачи.
 Одномерные задачи фильтрации вязкопластичной жидкости Поток плоскорадиален u kdr dp ( u >0); ( u =0). Формула притока dr dpk rh 2 Q u dr dp u =0, если dp / dr Установившееся течение вязкопластичной жидкости Интегрируем формулу притока при р( r c )=р c ; р( R к )=р к
Одномерные задачи фильтрации вязкопластичной жидкости Поток плоскорадиален u kdr dp ( u >0); ( u =0). Формула притока dr dpk rh 2 Q u dr dp u =0, если dp / dr Установившееся течение вязкопластичной жидкости Интегрируем формулу притока при р( r c )=р c ; р( R к )=р к
 кc c cc. Rrr , r r ln kh 2 Q rrp)r(p . ррp Rp при 0 Q ; Rp при Rp r R ln kh 2 Q скcкc c к Анализ • Часть разности давлений в виде линейного слагаемого с угловым коэффициентом теряется на преодоление предельного градиента сдвига. • При Q 0 давление не постоянно (как в случае фильтрации по закону Дарси), а изменяется по линейному закону. • При тех же условиях наличие предельного градиента давления в пласте ведет к уменьшению дебита скважины по сравнению с фильтрацией по закону Дарси (формула Дюпюи). • Индикаторная линия скважины Q ( р с ) — прямолинейная, но не проходит через начало координат, а отсекает на оси депрессий отрезок, равный R к. Распределение давления в пласте Дебит скважины
кc c cc. Rrr , r r ln kh 2 Q rrp)r(p . ррp Rp при 0 Q ; Rp при Rp r R ln kh 2 Q скcкc c к Анализ • Часть разности давлений в виде линейного слагаемого с угловым коэффициентом теряется на преодоление предельного градиента сдвига. • При Q 0 давление не постоянно (как в случае фильтрации по закону Дарси), а изменяется по линейному закону. • При тех же условиях наличие предельного градиента давления в пласте ведет к уменьшению дебита скважины по сравнению с фильтрацией по закону Дарси (формула Дюпюи). • Индикаторная линия скважины Q ( р с ) — прямолинейная, но не проходит через начало координат, а отсекает на оси депрессий отрезок, равный R к. Распределение давления в пласте Дебит скважины
 Слоистый пласт Индикаторные линии при плоскорадиальном течении вязкопластичной жидкости через трёхслойный пласт (у каждого пропластка свои значениями толщин, проницаемости и начального градиента) Неустановившаяся фильтрация вязкопластичной жидкости При решении нестационарных задач на основе модели фильтрации с предельным градиентом в пласте образуется переменная область фильтрации, на границе которой (пока она не достигнет границы пласта) модуль градиента давления должен равняться предельному градиенту а давление — начальному пластовому. Уравнение пьезопроводности: gradp 1 div t p æ,
Слоистый пласт Индикаторные линии при плоскорадиальном течении вязкопластичной жидкости через трёхслойный пласт (у каждого пропластка свои значениями толщин, проницаемости и начального градиента) Неустановившаяся фильтрация вязкопластичной жидкости При решении нестационарных задач на основе модели фильтрации с предельным градиентом в пласте образуется переменная область фильтрации, на границе которой (пока она не достигнет границы пласта) модуль градиента давления должен равняться предельному градиенту а давление — начальному пластовому. Уравнение пьезопроводности: gradp 1 div t p æ,
 Пуск скважины с постоянным дебитом при фильтрации вязкопластичной жидкости с предельным градиентом Из решения уравнения пьезопроводности получаем зависимость забойного давления от времени Основная роль при малом времени, когда преобладают упругие силы. При больших значениях времени kh 2 Q kh t. Q 3 rkh t. Q kh 6 Q pp 3 1 3 c кc ææ ln
Пуск скважины с постоянным дебитом при фильтрации вязкопластичной жидкости с предельным градиентом Из решения уравнения пьезопроводности получаем зависимость забойного давления от времени Основная роль при малом времени, когда преобладают упругие силы. При больших значениях времени kh 2 Q kh t. Q 3 rkh t. Q kh 6 Q pp 3 1 3 c кc ææ ln
 Образование застойных зон при вытеснении нефти водой — эффект фильтрации с предельным градиентом давления Схема образования застойных зон а — между двумя добывающими скважинами; b — при пятиточечной расстановке скважин (1 — нагнетательная скважина; 2 — добывающая скважина; 3 — зона застоя) Отношение незаштрихованных областей ко всей площади пятиточечной ячейки можно считать площадным коэффициентом охвата пласта заводнением.
Образование застойных зон при вытеснении нефти водой — эффект фильтрации с предельным градиентом давления Схема образования застойных зон а — между двумя добывающими скважинами; b — при пятиточечной расстановке скважин (1 — нагнетательная скважина; 2 — добывающая скважина; 3 — зона застоя) Отношение незаштрихованных областей ко всей площади пятиточечной ячейки можно считать площадным коэффициентом охвата пласта заводнением.
 ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ ФИЛЬТРАЦИИ ОБ УСТАНОВИВШЕМСЯ ПРИТОКЕ К СКВАЖИНЕ
ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ ФИЛЬТРАЦИИ ОБ УСТАНОВИВШЕМСЯ ПРИТОКЕ К СКВАЖИНЕ
 Рис. 1. 1. Зависимость суммарного дебита от числа скважин Два вида задач: 1. Задаётся дебит скважин и требуется определить необходимое для этого дебита забойное давление и, кроме того, давление в любой точке пласта. 2. Задаётся забойное давление и требуется определить дебит. Последний вид условия встречается наиболее часто в практике разработки НГМ Методы решения Суперпозиции (потенциалов) Комплексного переменного Комформного отображения
Рис. 1. 1. Зависимость суммарного дебита от числа скважин Два вида задач: 1. Задаётся дебит скважин и требуется определить необходимое для этого дебита забойное давление и, кроме того, давление в любой точке пласта. 2. Задаётся забойное давление и требуется определить дебит. Последний вид условия встречается наиболее часто в практике разработки НГМ Методы решения Суперпозиции (потенциалов) Комплексного переменного Комформного отображения
 Задача плоской интерференции (наложения) скважин. • Пласт — неограниченный, горизонтальный, имеет постоянную мощность и непроницаемые подошву и кровлю. • Пласт вскрыт множеством совершенных скважин и заполнен однородной жидкостью или газом. • Движение жидкости — установившееся, подчиняется закону Дарси и является плоским. Плоское движение — течение происходит в плоскостях, параллельных между собой и картина движения во всех плоскостях идентична. В связи с этим разбирается течение в одной из этих плоскостей — в основной плоскости течения.
Задача плоской интерференции (наложения) скважин. • Пласт — неограниченный, горизонтальный, имеет постоянную мощность и непроницаемые подошву и кровлю. • Пласт вскрыт множеством совершенных скважин и заполнен однородной жидкостью или газом. • Движение жидкости — установившееся, подчиняется закону Дарси и является плоским. Плоское движение — течение происходит в плоскостях, параллельных между собой и картина движения во всех плоскостях идентична. В связи с этим разбирается течение в одной из этих плоскостей — в основной плоскости течения.
 Метод СУПЕРПОЗИЦИИ При совместном действии в пласте нескольких стоков (эксплуатационных скважин) или источников (нагнетательных скважин) потенциальная функция, определяемая каждым стоком (источником), вычисляется по формуле для единственного стока (источника).
Метод СУПЕРПОЗИЦИИ При совместном действии в пласте нескольких стоков (эксплуатационных скважин) или источников (нагнетательных скважин) потенциальная функция, определяемая каждым стоком (источником), вычисляется по формуле для единственного стока (источника).
 Потенциальная функция, обусловленная всеми стоками (источниками), вычисляется путём алгебраического сложения этих независимых друг от друга значений потенциальной функции. Суммарная скорость фильтрации определяется как векторная сумма скоростей фильтрации, вызванная работой каждой скважины
Потенциальная функция, обусловленная всеми стоками (источниками), вычисляется путём алгебраического сложения этих независимых друг от друга значений потенциальной функции. Суммарная скорость фильтрации определяется как векторная сумма скоростей фильтрации, вызванная работой каждой скважины
 Потенциал группы скважин по принципу суперпозиции iii i Crln h 2 G Crln. G h 2 1 iii Потенциал скважины при плоскорадиальном потоке i 1 G i. Cr i Уравнение эквипотенциальных поверхностей при равенстве дебитов i 1 )G(sign i. Cr i Линии тока образуют семейство кривых, ортогональ-ных изобарам
Потенциал группы скважин по принципу суперпозиции iii i Crln h 2 G Crln. G h 2 1 iii Потенциал скважины при плоскорадиальном потоке i 1 G i. Cr i Уравнение эквипотенциальных поверхностей при равенстве дебитов i 1 )G(sign i. Cr i Линии тока образуют семейство кривых, ортогональ-ных изобарам
 Приток к совершенной скважине Фильтрационный поток от нагнетательной скважины к эксплуатационной Схема расположения источника 0 1 и стока 0 2 знаки дебитов: источник G 1 = — G , сток G 2 = + G. Исходная формула. Crln. G h 2 1 ii Для данной постановки C r r ln h 2 G Crln h 2 G
Приток к совершенной скважине Фильтрационный поток от нагнетательной скважины к эксплуатационной Схема расположения источника 0 1 и стока 0 2 знаки дебитов: источник G 1 = — G , сток G 2 = + G. Исходная формула. Crln. G h 2 1 ii Для данной постановки C r r ln h 2 G Crln h 2 G
 Уравнение изобар 1 21 C r r Линии изобар — окружности центры которых расположены на прямой, проходящей через центры скважин Семейство линий тока ортогонально изобарам и тоже окружности. Все линии тока проходят через сток и источник. Центры всех окружностей линий тока расположены на прямой, делящей расстояние между стоком и источником пополам
Уравнение изобар 1 21 C r r Линии изобар — окружности центры которых расположены на прямой, проходящей через центры скважин Семейство линий тока ортогонально изобарам и тоже окружности. Все линии тока проходят через сток и источник. Центры всех окружностей линий тока расположены на прямой, делящей расстояние между стоком и источником пополам
 , r a 2 ln h Gc эн т. к. на контуре эксплуатационной скважины , a 2 r r r c 21 а на контуре нагнетательной скважины c 21 r а 2 r r Массовая скорость фильтрации в любой точке пласта М находится по правилу суперпозиции сложения векторов скорости от действия источника и стока 21 rhr Ga u Время движения частицы от некоторой точки х 0 до точки х 2 0 2 3 0 3 axax 3 xx Qa hm t
, r a 2 ln h Gc эн т. к. на контуре эксплуатационной скважины , a 2 r r r c 21 а на контуре нагнетательной скважины c 21 r а 2 r r Массовая скорость фильтрации в любой точке пласта М находится по правилу суперпозиции сложения векторов скорости от действия источника и стока 21 rhr Ga u Время движения частицы от некоторой точки х 0 до точки х 2 0 2 3 0 3 axax 3 xx Qa hm t
 Время обводнения Т (х=0; х 0 =2 а) Qhma 34 T 2 Площадь обводнения из равенства объёмов TQ и mh . 2 а 34 Расстояние, пройденное частицей за время Т от нагнетательной скважины до эксплуатационной, вдвое больше расстояния пройденного другой частицей за это же время в положительном направлении оси х.
Время обводнения Т (х=0; х 0 =2 а) Qhma 34 T 2 Площадь обводнения из равенства объёмов TQ и mh . 2 а 34 Расстояние, пройденное частицей за время Т от нагнетательной скважины до эксплуатационной, вдвое больше расстояния пройденного другой частицей за это же время в положительном направлении оси х.
 Приток к группе скважин с удаленным контуром питания Схема группы скважин в пласте с удаленным контуром питания Дебиты из системы уравнений. Crln. G h 2 1 n ji, 1 j jijciiсi Crln. G h 2 1 n 1 j кjк Результат тем точнее, чем дальше точка отстоит от контура питания. Исходная формула Crln. G h 2 1 ii
Приток к группе скважин с удаленным контуром питания Схема группы скважин в пласте с удаленным контуром питания Дебиты из системы уравнений. Crln. G h 2 1 n ji, 1 j jijciiсi Crln. G h 2 1 n 1 j кjк Результат тем точнее, чем дальше точка отстоит от контура питания. Исходная формула Crln. G h 2 1 ii
 Приток к скважине в пласте с прямолинейным контуром питания Граничные условия: = к при r 1 = r 2 , т. е. при r 1 / r 2 =1; = с при r 1 = r с , r 2 2 а , т. е. при r 1 / r 2 r с /2 а; Исходная формула c ск r a 2 ln h 2 G C r r ln h 2 G Crln h 2 G 2 1 21 МЕТОД ОТОБРАЖЕНИЯ ИСТОЧНИКОВ (СТОКОВ) — для выполнения тех или иных условий на границах вводятся фиктивные стоки или источники за пределами пласта
Приток к скважине в пласте с прямолинейным контуром питания Граничные условия: = к при r 1 = r 2 , т. е. при r 1 / r 2 =1; = с при r 1 = r с , r 2 2 а , т. е. при r 1 / r 2 r с /2 а; Исходная формула c ск r a 2 ln h 2 G C r r ln h 2 G Crln h 2 G 2 1 21 МЕТОД ОТОБРАЖЕНИЯ ИСТОЧНИКОВ (СТОКОВ) — для выполнения тех или иных условий на границах вводятся фиктивные стоки или источники за пределами пласта
 Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы Данная задача может возникнуть при расположении добывающей скважины вблизи сброса или около границы выклинивания продуктивного пласта МЕТОД — отображения источника и стока Исходные формулы. Crln. G h 2 1 n ji, 1 j jijciiсi Crln. G h 2 1 n 1 j кjк а 2 r r lnh 2 G c 2 к сн
Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы Данная задача может возникнуть при расположении добывающей скважины вблизи сброса или около границы выклинивания продуктивного пласта МЕТОД — отображения источника и стока Исходные формулы. Crln. G h 2 1 n ji, 1 j jijciiсi Crln. G h 2 1 n 1 j кjк а 2 r r lnh 2 G c 2 к сн
 Приток к скважине в пласте с произвольным контуром питания Схема видов контуров питания 1. При вычислении дебита скважины форма внешнего контура пласта не имеет сколько-нибудь существенного значения. 2. Чем дальше от внешнего контура пласта находится скважина, тем меньший дебит она имеет. Однако, так как величина расстояния входит под знаком логарифма, то даже значительное изменение этого расстояния мало влияет на величину дебита 3. В случае расположения скважины эксцентрично относительно контура поток можно считать плоско-радиальным и дебит рассчитывать по формуле Дюпюи если r к. >10 3 r c и эксцентриситет а 1 < r к /2.
Приток к скважине в пласте с произвольным контуром питания Схема видов контуров питания 1. При вычислении дебита скважины форма внешнего контура пласта не имеет сколько-нибудь существенного значения. 2. Чем дальше от внешнего контура пласта находится скважина, тем меньший дебит она имеет. Однако, так как величина расстояния входит под знаком логарифма, то даже значительное изменение этого расстояния мало влияет на величину дебита 3. В случае расположения скважины эксцентрично относительно контура поток можно считать плоско-радиальным и дебит рассчитывать по формуле Дюпюи если r к. >10 3 r c и эксцентриситет а 1 < r к /2.
 Приток к бесконечным цепочкам и кольцевым батареям скважин Граничные условия : на контуре питания = к = const при r j = r к ; на контуре скважины = с = const при r 1 = r с ; r j (j 1)=2 a sin[(n-1) /n]. Исходные формулы. Crln. G h 2 1 n ji, 1 j jijciiсi Crln. G h 2 1 n 1 j кjк Приток к скважинам кольцевой батареи
Приток к бесконечным цепочкам и кольцевым батареям скважин Граничные условия : на контуре питания = к = const при r j = r к ; на контуре скважины = с = const при r 1 = r с ; r j (j 1)=2 a sin[(n-1) /n]. Исходные формулы. Crln. G h 2 1 n ji, 1 j jijciiсi Crln. G h 2 1 n 1 j кjк Приток к скважинам кольцевой батареи
 При данных гр. условиях: Crln h 2 Gn кк C n j sinra 2 ln h 2 G 1 n 1 j c 1 n с 1 n 1 n 1 j 2 n n j sin Т. к. , то Crna ln h 2 G c 1 n с Выражение для дебита одной скважины c 1 n n к ск rna r ln h 2 G Область применения: размеры пласта во много раз больше площади внутри окружности батареи скважин ( r к 10 а ) — случай водонапорного режима. n кc 1 n n 2 n 2 к ск rrna ar ln h 2 G — r к 10 а — случай режима растворенного газа
При данных гр. условиях: Crln h 2 Gn кк C n j sinra 2 ln h 2 G 1 n 1 j c 1 n с 1 n 1 n 1 j 2 n n j sin Т. к. , то Crna ln h 2 G c 1 n с Выражение для дебита одной скважины c 1 n n к ск rna r ln h 2 G Область применения: размеры пласта во много раз больше площади внутри окружности батареи скважин ( r к 10 а ) — случай водонапорного режима. n кc 1 n n 2 n 2 к ск rrna ar ln h 2 G — r к 10 а — случай режима растворенного газа
 Дебит батареи cк ск cn к ск бат r 2 n a 2 ln hn 2 1 а r ln h 2 1 n nr a а r ln h 2 G Поле течения в области действия круговой батареи Уравнение линий изобар 1 n 1 j 22 C n 1 j 2 cosar 2 ra Нейтральные линии тока Н — сходятся в центре батареи и делят расстояние между двумя соседними скважинами пополам. Главные линии тока Г — проходят через центры скважин и делят сектор, ограниченный двумя нейтральными линиями, пополам.
Дебит батареи cк ск cn к ск бат r 2 n a 2 ln hn 2 1 а r ln h 2 1 n nr a а r ln h 2 G Поле течения в области действия круговой батареи Уравнение линий изобар 1 n 1 j 22 C n 1 j 2 cosar 2 ra Нейтральные линии тока Н — сходятся в центре батареи и делят расстояние между двумя соседними скважинами пополам. Главные линии тока Г — проходят через центры скважин и делят сектор, ограниченный двумя нейтральными линиями, пополам.
 Скорость фильтрации по главным линиям максимальна, а по нейтральным линиям — минимальна. В центре кольцевой батареи скорость фильтрации равна нулю, т. е. частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Такие точки фильтрационного поля называются точками равновесия и при разработке в окрестностях таких точек образуются “застойные области”. Семейство изобар подразделяется на два подсемейства, которые разграничиваются изобарой пересекающей себя в центре батареи столько раз, сколько скважин составляет данную батарею. Первое подсемейство изобар определяет приток к отдельным скважинам и представляет собой замкнутые, каплеобразные кривые, описанные вокруг каждой скважины. Второе семейство — определяет приток к батарее в целом и представляет собой замкнутые кривые, описанные вокруг батареи.
Скорость фильтрации по главным линиям максимальна, а по нейтральным линиям — минимальна. В центре кольцевой батареи скорость фильтрации равна нулю, т. е. частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Такие точки фильтрационного поля называются точками равновесия и при разработке в окрестностях таких точек образуются “застойные области”. Семейство изобар подразделяется на два подсемейства, которые разграничиваются изобарой пересекающей себя в центре батареи столько раз, сколько скважин составляет данную батарею. Первое подсемейство изобар определяет приток к отдельным скважинам и представляет собой замкнутые, каплеобразные кривые, описанные вокруг каждой скважины. Второе семейство — определяет приток к батарее в целом и представляет собой замкнутые кривые, описанные вокруг батареи.
 Оценки эффекта взаимодействия скважин круговой батареи : дебит изменяется непропорционально числу скважин и радиусу батареи (расстоянию между скважинами); с увеличением числа скважин дебит каждой скважины уменьшается при постоянном забойном давлении, т. е. растет эффект взаимодействия; взаимодействие скважин может практически не проявляться только при очень больших расстояниях между скважинами (в случае несжимаемой жидкости, строго говоря, влияние скважин распространяется на весь пласт); с увеличением числа скважин темп роста суммарного дебита батареи замедляется т. е. сверх определённого предела увеличение числа скважин оказывается неэффективным в виду прекращения прироста дебита.
Оценки эффекта взаимодействия скважин круговой батареи : дебит изменяется непропорционально числу скважин и радиусу батареи (расстоянию между скважинами); с увеличением числа скважин дебит каждой скважины уменьшается при постоянном забойном давлении, т. е. растет эффект взаимодействия; взаимодействие скважин может практически не проявляться только при очень больших расстояниях между скважинами (в случае несжимаемой жидкости, строго говоря, влияние скважин распространяется на весь пласт); с увеличением числа скважин темп роста суммарного дебита батареи замедляется т. е. сверх определённого предела увеличение числа скважин оказывается неэффективным в виду прекращения прироста дебита.
 Приток к прямолинейной батарее скважин Режим: удаленный контур питания и постоянные забойные давления Состав по числу скважин : четный и нечетный Величина дебитов скважин: равноудаленные от середины или от концов батареи — одинаковы, а при разной удаленности — отличаются. Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико-геологических характеристик пласта и от физических параметров жидкости. Эффекты взаимодействия
Приток к прямолинейной батарее скважин Режим: удаленный контур питания и постоянные забойные давления Состав по числу скважин : четный и нечетный Величина дебитов скважин: равноудаленные от середины или от концов батареи — одинаковы, а при разной удаленности — отличаются. Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико-геологических характеристик пласта и от физических параметров жидкости. Эффекты взаимодействия
 Формула Голосова П. П. для общего дебита скважин прямолинейной батареи: — для нечетного числа скважин 2 n +1 , где n — любое целое число n 1 j 2 2 c cк бат j L ln r L ln 1 n 2 h 2 G — для четного числа скважин n 2 j 22 c 2 cк бат 1 j j L ln r L ln hn 4 G Здесь h — толщина пласта; — расстояние между скважинами; L – расстояние до контура. Ошибка в определении дебитов по данным формулам не превышает 3 -4% при L =10 км, r с =10 см, при расстояниях между скважинами 100 м 500 м.
Формула Голосова П. П. для общего дебита скважин прямолинейной батареи: — для нечетного числа скважин 2 n +1 , где n — любое целое число n 1 j 2 2 c cк бат j L ln r L ln 1 n 2 h 2 G — для четного числа скважин n 2 j 22 c 2 cк бат 1 j j L ln r L ln hn 4 G Здесь h — толщина пласта; — расстояние между скважинами; L – расстояние до контура. Ошибка в определении дебитов по данным формулам не превышает 3 -4% при L =10 км, r с =10 см, при расстояниях между скважинами 100 м 500 м.
 Фильтрационное поле бесконечной цепочки равностоящих скважин Формула дебита из формулы дебита скважин круговой батареи при r к = L + a ; a = n /(2 ), где L = const — разность между радиусом контура питания и радиусом кольцевой батареи а ; = const — длина дуги окружности радиусом а между двумя соседними скважинами кольцевой батареи. c 1 n n к ск rna r ln h 2 G Подставим значения r к , a
Фильтрационное поле бесконечной цепочки равностоящих скважин Формула дебита из формулы дебита скважин круговой батареи при r к = L + a ; a = n /(2 ), где L = const — разность между радиусом контура питания и радиусом кольцевой батареи а ; = const — длина дуги окружности радиусом а между двумя соседними скважинами кольцевой батареи. c 1 n n к ск rna r ln h 2 G Подставим значения r к , a
 с z 1 nz ск с n ск r 2 ln zn 1 1 ln h 2 r 2 ln n l 2 1 ln h 2 G Где z = / (2 L ), nz hz nz 1 1 lim =е Массовый дебит скважин линейной батареи с ск r 2 ln L 2 h 2 G Здесь L — расстояние от контура питания до батареи; — расстояние между скважинами батареи; h — толщина пласта.
с z 1 nz ск с n ск r 2 ln zn 1 1 ln h 2 r 2 ln n l 2 1 ln h 2 G Где z = / (2 L ), nz hz nz 1 1 lim =е Массовый дебит скважин линейной батареи с ск r 2 ln L 2 h 2 G Здесь L — расстояние от контура питания до батареи; — расстояние между скважинами батареи; h — толщина пласта.
 Массовый дебит батареи из n скважин с ск r 2 ln hn 2 1 nh L G Для несжимаемой жидкости с ск rhnknh L pp Q 2 ln k
Массовый дебит батареи из n скважин с ск r 2 ln hn 2 1 nh L G Для несжимаемой жидкости с ск rhnknh L pp Q 2 ln k
 Главные Г и нейтральные Н линии тока перпендикулярны цепочке. Нейтральными линиями тока вся плоскость течения делится на бесконечное число полос, каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями. Изобара, бесчисленное множество раз пересекающая сама себя, отделяет изобары внешнего течения ко всей батареи, охватывающих всю цепочку скважин, от изобар притока к скважине, охватывающих только данную скважину. Точки пересечения граничной изобары являются точками равновесия.
Главные Г и нейтральные Н линии тока перпендикулярны цепочке. Нейтральными линиями тока вся плоскость течения делится на бесконечное число полос, каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями. Изобара, бесчисленное множество раз пересекающая сама себя, отделяет изобары внешнего течения ко всей батареи, охватывающих всю цепочку скважин, от изобар притока к скважине, охватывающих только данную скважину. Точки пересечения граничной изобары являются точками равновесия.
 Метод эквивалентных фильтрационных сопротивлений (метод Борисова) Метод позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки — к одиночно работающей скважине и к одиночно работающей батареи. с ск r 2 ln hn 2 1 nh L G закон Ома I = U / R Дебит прямолин. батареи сопротивления внешнее внутреннее
Метод эквивалентных фильтрационных сопротивлений (метод Борисова) Метод позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки — к одиночно работающей скважине и к одиночно работающей батареи. с ск r 2 ln hn 2 1 nh L G закон Ома I = U / R Дебит прямолин. батареи сопротивления внешнее внутреннее
 Внешнее фильтрационное сопротивление — выражает фильтрационное сопротивление потоку от контура питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в предположении замены батареи галереей. Дебит равен дебиту в прямолинейно-параллельном потоке через площадь величиной n h на длине L . Внутреннее сопротивление — выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам за счет искривлений линий тока Дебит равен суммарному дебиту n скважин при плоскорадиальном течении, в предположении, что каждая скважина окружена контуром питания длиной ( аналог формулы Дюпюи) nkh L nh L р или
Внешнее фильтрационное сопротивление — выражает фильтрационное сопротивление потоку от контура питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в предположении замены батареи галереей. Дебит равен дебиту в прямолинейно-параллельном потоке через площадь величиной n h на длине L . Внутреннее сопротивление — выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам за счет искривлений линий тока Дебит равен суммарному дебиту n скважин при плоскорадиальном течении, в предположении, что каждая скважина окружена контуром питания длиной ( аналог формулы Дюпюи) nkh L nh L р или
 Сопротивления кольцевой батарея ar ln h 2 1 к Внешнее cr 2 n a 2 ln hn 2 1 Внутреннее Схема одной батареи Электрическая схема одной батареи области внутреннего сопротивления — затемнены. .
Сопротивления кольцевой батарея ar ln h 2 1 к Внешнее cr 2 n a 2 ln hn 2 1 Внутреннее Схема одной батареи Электрическая схема одной батареи области внутреннего сопротивления — затемнены. .
 «n» нагнетательных и эксплуатационных батарей a) b) Схема n- батарей с двумя контурами питания а) линейные батареи; b) кольцевые батареи
«n» нагнетательных и эксплуатационных батарей a) b) Схема n- батарей с двумя контурами питания а) линейные батареи; b) кольцевые батареи
 . Электрическая схема n- батарей с двумя контурами питания Сопротивления прямолинейная батарея круговая батареяci i i i r 2 ln h 2 1 ; hk L ci i 1 i i r 2 ln h 2 1 ; r r ln h
. Электрическая схема n- батарей с двумя контурами питания Сопротивления прямолинейная батарея круговая батареяci i i i r 2 ln h 2 1 ; hk L ci i 1 i i r 2 ln h 2 1 ; r r ln h
 Законы Кирхгоффа n 1 i i 0 G 1. 2. iiiii. GG для последовательных сопротивлений = i , а для параллельных — . 11 i Приведенные формулы тем точнее, чем больше расстояние между батареями по сравнению с половиной расстояния между скважинами Схема замены соседних батарей скважин одной батареей
Законы Кирхгоффа n 1 i i 0 G 1. 2. iiiii. GG для последовательных сопротивлений = i , а для параллельных — . 11 i Приведенные формулы тем точнее, чем больше расстояние между батареями по сравнению с половиной расстояния между скважинами Схема замены соседних батарей скважин одной батареей
 Интерференция несовершенных скважин 1) Определяется дебит совершенных скважин с радиусами r с по формулам теории интерференции для притока к стокам и источникам на плоскости. 2) Фильтрационное сопротивление каждой скважины увеличивается на величину коэффициентов несовершенства С i ( i = 1, . . . , 4). 3) Используется метод эквивалентных фильтрационных сопротивлений для исследования интерференции несовершенных скважин, в том числе при двухчленном законе фильтрации в виде. QАQр — нелинейное сопротивление, добавляемое к внутреннему сопротивлению . )Q(BQ
Интерференция несовершенных скважин 1) Определяется дебит совершенных скважин с радиусами r с по формулам теории интерференции для притока к стокам и источникам на плоскости. 2) Фильтрационное сопротивление каждой скважины увеличивается на величину коэффициентов несовершенства С i ( i = 1, . . . , 4). 3) Используется метод эквивалентных фильтрационных сопротивлений для исследования интерференции несовершенных скважин, в том числе при двухчленном законе фильтрации в виде. QАQр — нелинейное сопротивление, добавляемое к внутреннему сопротивлению . )Q(BQ
 Взаимодействие скважин в неоднородно проницаемом и анизотропном пластах n 0 к 2 c 1 n n 0 1 ск 21 RR ln k 1 rna R ln k 1 ФФh 2 GGG Исходные соотношения для дебитов: 1 -ая зона — c 1 n n 0 с0 rna R ln h 2 G 2 -ая зона — 0 к 0 к R R lnn h 2 G = k Ф+С , где dp. Ф Исключим 0 А) Кольцевая батарея во внутренней области
Взаимодействие скважин в неоднородно проницаемом и анизотропном пластах n 0 к 2 c 1 n n 0 1 ск 21 RR ln k 1 rna R ln k 1 ФФh 2 GGG Исходные соотношения для дебитов: 1 -ая зона — c 1 n n 0 с0 rna R ln h 2 G 2 -ая зона — 0 к 0 к R R lnn h 2 G = k Ф+С , где dp. Ф Исключим 0 А) Кольцевая батарея во внутренней области
 Анализ формулы: 1) При k 1 / k 2 = 1, то U будет меньше его значения в однородном пласте. G G Ui Б) Кольцевая батарея во внешней области ( а > R 0 ). n 2 0 n 2 12 12 c 1 n n к ск Ra a ln kk kk rna R ln ФФh 2 G
Анализ формулы: 1) При k 1 / k 2 = 1, то U будет меньше его значения в однородном пласте. G G Ui Б) Кольцевая батарея во внешней области ( а > R 0 ). n 2 0 n 2 12 12 c 1 n n к ск Ra a ln kk kk rna R ln ФФh 2 G
 Анизотропный пласт Эффект взаимодействия будет значительно усиленным или ослабленным лишь при резком различии проницаемостей в двух определённых направлениях: в направлении линии расстановки скважин и в направлении перпендикулярном к этой линии. Ослабление взаимодействия наблюдается в случае более низкой проницаемости в направлении линии расстановки скважин по сравнению с проницаемостью в перпендикулярном направлении. Усиление эффекта взаимодействия происходит в обратном случае. Таким образом, для уменьшения эффекта взаимодействия при закладывании новых скважин следует выбирать направление, в котором пласт наименее проницаем.
Анизотропный пласт Эффект взаимодействия будет значительно усиленным или ослабленным лишь при резком различии проницаемостей в двух определённых направлениях: в направлении линии расстановки скважин и в направлении перпендикулярном к этой линии. Ослабление взаимодействия наблюдается в случае более низкой проницаемости в направлении линии расстановки скважин по сравнению с проницаемостью в перпендикулярном направлении. Усиление эффекта взаимодействия происходит в обратном случае. Таким образом, для уменьшения эффекта взаимодействия при закладывании новых скважин следует выбирать направление, в котором пласт наименее проницаем.
 Взаимодействие скважин c 1 n n к 1 x rna R ln xln rna R ln GG у nln r a ln nln xr a ln у 1 n c В центре батареи действует нагнетательная скважина с дебитом равным дебиту батареи. Сравнение дебитов скважин кольцевой батареи из n эксплуатационных скважин в двух случаях: 1)скважины имеют радиус r c и 2)скважины имеют радиус х r c.
Взаимодействие скважин c 1 n n к 1 x rna R ln xln rna R ln GG у nln r a ln nln xr a ln у 1 n c В центре батареи действует нагнетательная скважина с дебитом равным дебиту батареи. Сравнение дебитов скважин кольцевой батареи из n эксплуатационных скважин в двух случаях: 1)скважины имеют радиус r c и 2)скважины имеют радиус х r c.
 Анализ 1) с увеличением числа эксплуатационных скважин кольцевой батареи влияние их радиуса на дебит уменьшается, если отсутствует нагнетание жидкости в пласт; 2) если в центре батареи находится нагнетательная скважина, то влияние радиуса скважины на дебит будет больше, чем при отсутствии центрального нагнетания жидкости в пласт. 3) радиус скважины влияет на производительность больше, чем при одиночной эксплуатационной скважине. Число скважин мало влияет на производительность.
Анализ 1) с увеличением числа эксплуатационных скважин кольцевой батареи влияние их радиуса на дебит уменьшается, если отсутствует нагнетание жидкости в пласт; 2) если в центре батареи находится нагнетательная скважина, то влияние радиуса скважины на дебит будет больше, чем при отсутствии центрального нагнетания жидкости в пласт. 3) радиус скважины влияет на производительность больше, чем при одиночной эксплуатационной скважине. Число скважин мало влияет на производительность.
 Взаимодействие скважин при неустановившихся процессах По методу суперпозиции n — число скважин ; Q j — объемный дебит стока (+) или источника(-) за номером j ; р -понижение давления в какой либо точке пласта; r j — расстояние данной точки пласта от скважины за номером j Данная зависимость используется для расчета параметров пласта путем обработки кривой восстановления давления в случае скважины, эксплуатирующейся в течение длительного времени и остановленной для исследования. n j j jj ætr Ei. Q hkp 1 1 2 44 ð n j jjj r æt, Q hkp 1 1 22462 4 lnð
Взаимодействие скважин при неустановившихся процессах По методу суперпозиции n — число скважин ; Q j — объемный дебит стока (+) или источника(-) за номером j ; р -понижение давления в какой либо точке пласта; r j — расстояние данной точки пласта от скважины за номером j Данная зависимость используется для расчета параметров пласта путем обработки кривой восстановления давления в случае скважины, эксплуатирующейся в течение длительного времени и остановленной для исследования. n j j jj ætr Ei. Q hkp 1 1 2 44 ð n j jjj r æt, Q hkp 1 1 22462 4 lnð
 ОСНОВЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ МНОГОКОМПАНЕНТНОЙ ФИЛЬТРАЦИИ В основе всех современных методов прогнозирования показателей разработки месторождений природных углеводородов лежат численные методы интегрирования соответствующих дифференциальных уравнений в частных производных, описывающих процессы двухмерной или трехмерной многофазной фильтрации, и расчету картин двухмерных и трехмерных фильтрационных течений на их основе
ОСНОВЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ МНОГОКОМПАНЕНТНОЙ ФИЛЬТРАЦИИ В основе всех современных методов прогнозирования показателей разработки месторождений природных углеводородов лежат численные методы интегрирования соответствующих дифференциальных уравнений в частных производных, описывающих процессы двухмерной или трехмерной многофазной фильтрации, и расчету картин двухмерных и трехмерных фильтрационных течений на их основе
 Сущность математического моделирования Сущность моделирования процессов фильтрации флюидов в пластах заключается в определении количественной связи между дебитами и давлениями на забоях скважин и определенных контурах, скоростей и сроков перемещения отдельных частиц пластовой жидкости в зависимости от формы залежи, параметров пласта, вязкости флюидов, числа и расположения скважин.
Сущность математического моделирования Сущность моделирования процессов фильтрации флюидов в пластах заключается в определении количественной связи между дебитами и давлениями на забоях скважин и определенных контурах, скоростей и сроков перемещения отдельных частиц пластовой жидкости в зависимости от формы залежи, параметров пласта, вязкости флюидов, числа и расположения скважин.
 Прямые задачи Задачи, в которых свойства пласта и жидкостей, а также «начальные и граничные» условия считаются известными. Важнейшие прямые активные задачи — определение полей давлений, нефтенасыщенности и водонасыщенности в нефтяном пласте — объекте разработки с системой скважин. Важнейшие прямые пассивные задачи — определение конфигурации подвижной границы нефтяной зоны и скорости ее продвижения с целью установления сроков прорыва вытесняющего флюида в скважины и вычисления текущего коэффициента нефтеотдачи.
Прямые задачи Задачи, в которых свойства пласта и жидкостей, а также «начальные и граничные» условия считаются известными. Важнейшие прямые активные задачи — определение полей давлений, нефтенасыщенности и водонасыщенности в нефтяном пласте — объекте разработки с системой скважин. Важнейшие прямые пассивные задачи — определение конфигурации подвижной границы нефтяной зоны и скорости ее продвижения с целью установления сроков прорыва вытесняющего флюида в скважины и вычисления текущего коэффициента нефтеотдачи.
 Обратные задачи «Активные» обратные задачи — задачи управления, регулирования процесса разработки пласта или месторождения. «Пассивные» обратные задачи — распознавание объектов разработки и уточнение представления о состоянии и свойствах пластовой системы.
Обратные задачи «Активные» обратные задачи — задачи управления, регулирования процесса разработки пласта или месторождения. «Пассивные» обратные задачи — распознавание объектов разработки и уточнение представления о состоянии и свойствах пластовой системы.
 Типы моделей Двухфазная модель — моделирование процессов вытеснения нефти водой при давлениях, выше давления насыщения нефти газом Трехфазная модель фильтрации нефти, газа и воды — моделирование разработки нефтегазовых залежей при существенном влиянии гравитационного разделения фаз на процесс разработки, при прогнозировании эффективности процесса закачки воды и газа Композиционные модели — для расчета процесса разработки газоконденсатных пластов, оценки эффективности отдельных методов увеличения нефтеотдачи пластов, т. е. при рассмотрении нефти как смеси углеводородных компонентов Особенности исследовательских и коммерческих программных систем — «симуляторов»
Типы моделей Двухфазная модель — моделирование процессов вытеснения нефти водой при давлениях, выше давления насыщения нефти газом Трехфазная модель фильтрации нефти, газа и воды — моделирование разработки нефтегазовых залежей при существенном влиянии гравитационного разделения фаз на процесс разработки, при прогнозировании эффективности процесса закачки воды и газа Композиционные модели — для расчета процесса разработки газоконденсатных пластов, оценки эффективности отдельных методов увеличения нефтеотдачи пластов, т. е. при рассмотрении нефти как смеси углеводородных компонентов Особенности исследовательских и коммерческих программных систем — «симуляторов»
 Процедура адаптации математической модели к известной истории разработки месторождений и работы скважин состоит в согласовании результатов расчетов техноло-гических показателей предшествующего периода с фактической динамикой разработки. Адаптация модели связана с уточнением фильтрационных и емкостных параметров пласта, функций относительных фазовых проницаемостей для нефти, газа и воды, энергетических характеристик пласта — поля давлений, оценки выработки запасов нефти на отдельных участках пластов. В результате адаптации уточняются размеры законтурной области, начальные и остаточные геологические запасы нефти и газа, проницаемость и гидропроводность пласта, коэффициенты продуктивности и приемистости, функции модифицированных фазовых проницаемостей, функции адсорбции и десорбции.
Процедура адаптации математической модели к известной истории разработки месторождений и работы скважин состоит в согласовании результатов расчетов техноло-гических показателей предшествующего периода с фактической динамикой разработки. Адаптация модели связана с уточнением фильтрационных и емкостных параметров пласта, функций относительных фазовых проницаемостей для нефти, газа и воды, энергетических характеристик пласта — поля давлений, оценки выработки запасов нефти на отдельных участках пластов. В результате адаптации уточняются размеры законтурной области, начальные и остаточные геологические запасы нефти и газа, проницаемость и гидропроводность пласта, коэффициенты продуктивности и приемистости, функции модифицированных фазовых проницаемостей, функции адсорбции и десорбции.
 Необходимые исходные данные для построения геологических и фильтрационных моделей, адекватных реальным объектам геологические модели: данные сейсморазведки и их интерпретации, результаты анализов и исследований кернов, результаты исследований промысловой геофизики, их интерпретации, данные инклинометрии скважин, сведения о составах и минерализации грунтовых вод и т. д. фильтрационные модели: результаты интерпретации геофизических и гидродинамических исследований скважин, помесячная история разработки месторождений, координаты скважин и режимы их работы, значения пластовых и забойных давлений в скважинах и другая информация
Необходимые исходные данные для построения геологических и фильтрационных моделей, адекватных реальным объектам геологические модели: данные сейсморазведки и их интерпретации, результаты анализов и исследований кернов, результаты исследований промысловой геофизики, их интерпретации, данные инклинометрии скважин, сведения о составах и минерализации грунтовых вод и т. д. фильтрационные модели: результаты интерпретации геофизических и гидродинамических исследований скважин, помесячная история разработки месторождений, координаты скважин и режимы их работы, значения пластовых и забойных давлений в скважинах и другая информация
 Актуальность математического моделирования грамотное использование результатов моделирования реально увеличивает коэффициент нефтеотдачи на 5 — 10%, дополнительная добыча нефти составляет 5 — 25%.
Актуальность математического моделирования грамотное использование результатов моделирования реально увеличивает коэффициент нефтеотдачи на 5 — 10%, дополнительная добыча нефти составляет 5 — 25%.
 Основные проблемы математического моделирования Невозможность полноразмерного моделирования Недостаточное развитие теоретических основ проектирования разработки месторождений скважинами сложного профиля и методов расчета групп скважин различного профиля Недостаточная точность расчета сложных фильтрационных процессов в окрестности скважин и вблизи высокопроводящих трещин сложных конфигураций, образующихся при гидроразрыве Сложность моделирования пластов сложных конфигураций, с нетривиальными условиями на внутренних и внешних границах пласта — контурах питания, при наличии тектонических и других нарушений в строении пластов наличие у искомых решений соответствующих математических задач особых точек (в случае вертикальных и наклонно-ориентированных скважин), линий и кривых (для горизонтальных и горизонтально-ветвящихся скважин) или особых поверхностей (для фронтов вытеснения, различных геологических нарушений строения пласта, трещин гидроразрыва, образований макроцеликов).
Основные проблемы математического моделирования Невозможность полноразмерного моделирования Недостаточное развитие теоретических основ проектирования разработки месторождений скважинами сложного профиля и методов расчета групп скважин различного профиля Недостаточная точность расчета сложных фильтрационных процессов в окрестности скважин и вблизи высокопроводящих трещин сложных конфигураций, образующихся при гидроразрыве Сложность моделирования пластов сложных конфигураций, с нетривиальными условиями на внутренних и внешних границах пласта — контурах питания, при наличии тектонических и других нарушений в строении пластов наличие у искомых решений соответствующих математических задач особых точек (в случае вертикальных и наклонно-ориентированных скважин), линий и кривых (для горизонтальных и горизонтально-ветвящихся скважин) или особых поверхностей (для фронтов вытеснения, различных геологических нарушений строения пласта, трещин гидроразрыва, образований макроцеликов).
 Большое время счета и использование значительной памяти Необходимость перехода от сеточных методов к к методам конечных элементов, граничных интегральных уравнений и им подобным в случае расчета скважин сложного профиля, трещин гидроразрыва
Большое время счета и использование значительной памяти Необходимость перехода от сеточных методов к к методам конечных элементов, граничных интегральных уравнений и им подобным в случае расчета скважин сложного профиля, трещин гидроразрыва
