ПОДЗЕМНАЯ ГИДРОДИНАМИКА Комплексное переменное 1 Решение плоских

ПОДЗЕМНАЯ ГИДРОДИНАМИКА Комплексное переменное 1

Решение плоских задач фильтрации методами теории функций комплексного переменного 2

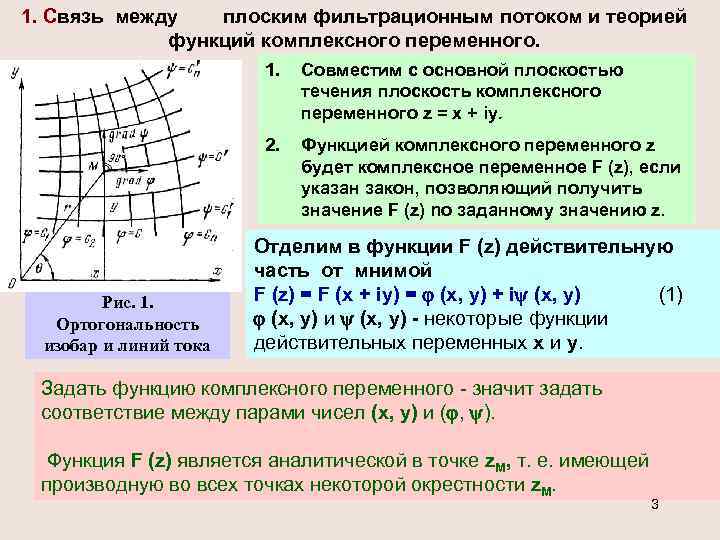1. Связь между плоским фильтрационным потоком и теорией функций комплексного переменного. 1. 2. Рис. 1. Ортогональность изобар и линий тока Совместим с основной плоскостью течения плоскость комплексного переменного z = х + iy. Функцией комплексного переменного z будет комплексное переменное F (z), если указан закон, позволяющий получить значение F (z) no заданному значению z. Отделим в функции F (z) действительную часть от мнимой F (z) = F (х + iy) = (х, у) + i (х, у) (1) (х, у) и (х, у) - некоторые функции действительных переменных х и у. Задать функцию комплексного переменного - значит задать соответствие между парами чисел (х, у) и ( , ). Функция F (z) является аналитической в точке z. М, т. е. имеющей производную во всех точках некоторой окрестности z. М. 3

Положения теории функций комплексного переменного 1. Каждые две кривые, из которых одна принадлежит семейству кривых, определяемых уравнением (х, у) = С, а другая - семейству кривых (х, у) = С* (С и С* — постоянные), пересекаются под прямым углом, т. е. два семейства кривых образуют ортогональную сетку в основной плоскости течения. 2. Функции (х, у) и (х, у) удовлетворяют уравнению Лапласа, т, е. Положения 2 справедливы, если выполняются условия: Условия (3) называются уравнениями Коши — Римана. 4

Характеристическая функция, потенциал и функция тока 1. Плоский фильтрационный поток любой жидкости или газа подчиняется закону Дарси. Кривые (х, у) = С - эквипотенциальные линии (для несжимаемой жидкости – изобары) Кривые (х, у) = С* взаимно ортогональны с эквипотенциальными линиями и, следовательно, направление векторов скорости фильтрации будет совпадать в любой данной точке М с направлением касательной к кривой семейства (х, у) = С*, т. е. кривые этого семейства можно считать линиями тока. (При установившемся движении линии тока и траектории частиц жидкости совпадают). Функция (х, у) называется функцией тока. Потенциальная функция течения и функция тока равны действительной и мнимой части некоторой функции F (z) комплексного переменного z Функция F (z) называется характеристической функцией течения (комплексным потенциалом). По эквипотенциальным линиям определяется распределение давлений в 5 пласте, по линиям тока - направление движения и характер поля скоростей фильтрации.

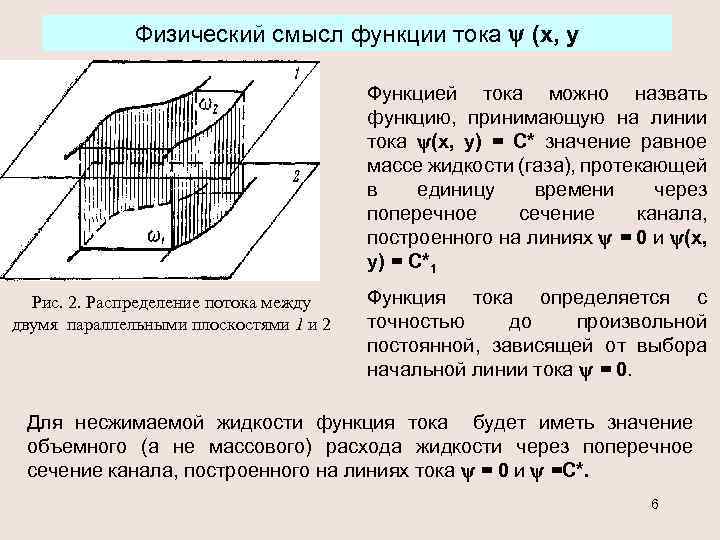Физический смысл функции тока (х, у Функцией тока можно назвать функцию, принимающую на линии тока (х, у) = С* значение равное массе жидкости (газа), протекающей в единицу времени через поперечное сечение канала, построенного на линиях = 0 и (х, у) = С*1 Рис. 2. Распределение потока между двумя параллельными плоскостями 1 и 2 Функция тока определяется с точностью до произвольной постоянной, зависящей от выбора начальной линии тока = 0. Для несжимаемой жидкости функция тока будет иметь значение объемного (а не массового) расхода жидкости через поперечное сечение канала, построенного на линиях тока = 0 и =С*. 6

Порядок исследования плоских течений с помощью комплексного переменного 1. Определяем характеристическую функцию, соответствующую данной задаче. 2. Отделяем в характеристической функции действительную часть от мнимой, т. е. определяем потенциальную функцию (х, у) и функцию тока (х, у). 3. Принимая различные значения функции , получаем уравнения семейства эквипотенциальных линий (х, у) = С, а придавая различные значения , находим уравнения семейства линий тока (х, у) = С*. 4. По эквипотенциальным линиям определяем распределение давлений в пласте, по линиям тока - направление движения и характер поля скоростей фильтрации. 5. Находим проекции вектора массовой скорости 6. Определяем массовую скорость 7

Определение массовой скорости Массовая скорость фильтрации равна производной от характеристической функции F (z) по комплексному аргументу z. Вынося во второй скобке множитель i за знак скобки и воспользовавшись уравнениями Коши - Римана получим: Учитывая (4): 8

Модуль производной от характеристической функции течения равен модулю массовой скорости фильтрации Модуль производной от характеристической функции течения для несжимаемой жидкости будет равен скорости (а не массовой скорости) фильтрации жидкости u. 9

2. Характеристические функции некоторых основных типов плоского потока Исследуем течения, заданные характеристическими функциями вида F(z) = Az и F(z) = Alnz. I. Плоско-параллельный поток F(z) = Az, где z = x +iy, A - любое комплексное или действительное число (А = А 1 + i. A 2 ) Отсюда Уравнение семейства эквипотенциальных линий - А 1 х – А 2 y = С. (7) Из (7): эквипотенциальные линии - прямые с угловым коэффициентом A 1/А 2. Уравнение семейства линий тока - А 1 у + А 2 х = С**. (8) Из (8): линии тока -- прямые с угловым коэффициентом (-A 2/А 1). 10

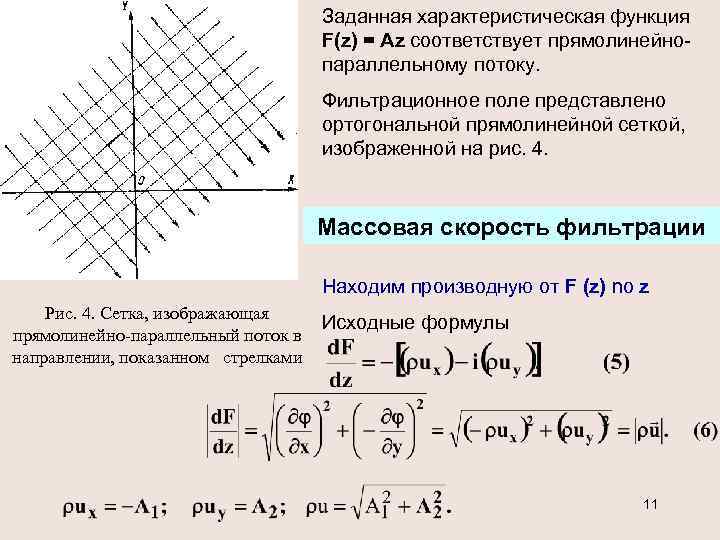Заданная характеристическая функция F(z) = Az соответствует прямолинейнопараллельному потоку. Фильтрационное поле представлено ортогональной прямолинейной сеткой, изображенной на рис. 4. Массовая скорость фильтрации Находим производную от F (z) no z Рис. 4. Сетка, изображающая прямолинейно-параллельный поток в направлении, показанном стрелками Исходные формулы 11

II. Плоско-радиальный поток А) F(z) = A ln z, где А — некоторое действительное число z– в полярных координатах: z = х +i y = r (cos θ + i sin θ) = reiθ, где г — радиус - вектор точки; θ — полярный угол. F(z) = A In (reiθ) = A In r + i. Aθ. =Alnr; =Aθ. Уравнение эквипотенциальных линий - r=const (9) Эквипотенциальные линии - концентрическими окружностями с центром в начале координат Уравнение линии тока - θ = const. (10) Линии тока - прямые, проходящие через начало координат. Рис. 5. Карта эквипотенциальных линий и линий тока при плоско-радиальном (сходящийся или расходящийся) потоке. Центр скважины (сток или источник) находится в начале координат. 12

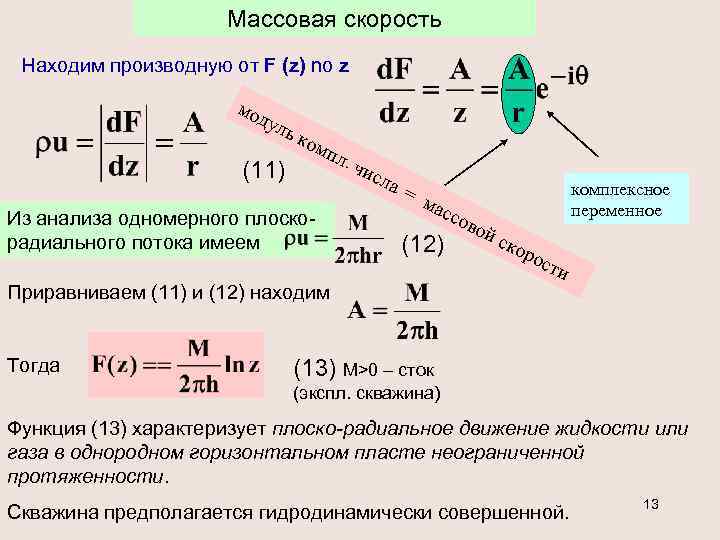Массовая скорость Находим производную от F (z) no z мо дул ьк (11) ом пл. Из анализа одномерного плоскорадиального потока имеем чис ла = мас (12) сов о комплексное переменное йс кор ост и Приравниваем (11) и (12) находим Тогда (13) М>0 – сток (экспл. скважина) Функция (13) характеризует плоско-радиальное движение жидкости или газа в однородном горизонтальном пласте неограниченной протяженности. Скважина предполагается гидродинамически совершенной. 13

B) где а = а 1 + ia 2 Течение плоско-радиальное, но особая точка, в которой помещается точечный сток или точечный источник, сдвинута в направлении оси 0 х на расстояние а 1, а в направлении оси-0 y на расстояние a 2 и, следовательно, центр поперечного сечения скважины находится не в начале координат, а в точке а = а 1 + ia 2. z-а– в полярных координатах (г — расстояние любой точки плоскости потока не до начала координат, а до особой точки а = а 1 + ia 2, в которой помещается сток или источник; θ— полярный угол с вершиной в особой точке). Отсюда: 14

III. Несколько точечных стоков и источников Потенциальную функцию течения и функцию тока ψ, поддерживаемых всеми стоками и источниками, можно определить по методу суперпозиции, как алгебраическую сумму потенциальных функций течений или функций тока, поддерживаемых отдельными стоками и источниками, если бы каждый из них был единственным в пласте. Характеристическая функция сложного потока Fj (z) - характеристическая функция, соответствующая стоку или источнику за номером j, находящемуся в точке аj: 15

Характеристическая функция течения при совместном действии источника и стока Характеристическая функция течения от нагнетательной скважины к эксплуатационной Рис. 6. Схема расположения источника 01 и стока 02 Отделяем действительную часть от мнимой 16

Тогда Уравнение семейства изобар Уравнение линий тока (14) θ 1 - θ 2=С* (15) а 2 -a 1=2 a 17

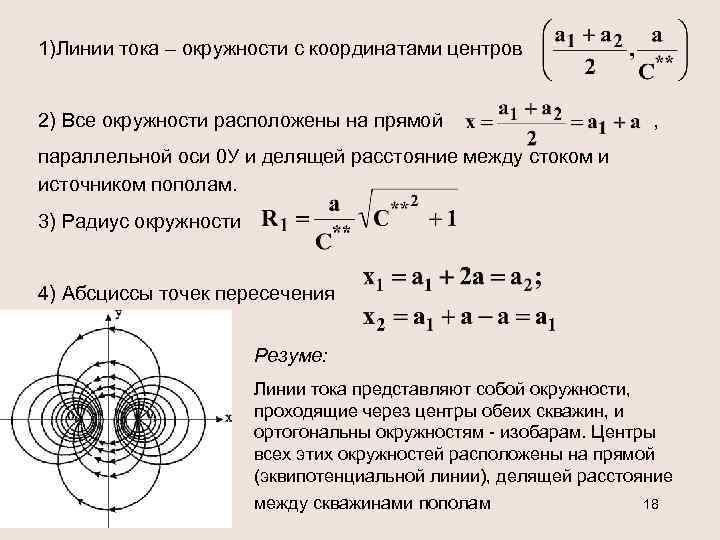1)Линии тока – окружности с координатами центров 2) Все окружности расположены на прямой , параллельной оси 0 У и делящей расстояние между стоком и источником пополам. 3) Радиус окружности 4) Абсциссы точек пересечения Резуме: Линии тока представляют собой окружности, проходящие через центры обеих скважин, и ортогональны окружностям - изобарам. Центры всех этих окружностей расположены на прямой (эквипотенциальной линии), делящей расстояние между скважинами пополам 18

Характеристическая функция течения для кольцевой батареи скважин Характеристическая функция для n стоков Для плоско-радиального притока (аj — комплексное число, определяющее положение стока за номером j). Заменим z на аj, r на а (радиус батареи), аj представим в тригонометрической форме где 19

Модуль массовой скорости фильтрации : где z = rei ; r 1, r 2, . . . , гn — расстояния точки пласта от стоков O 1, О 2 , . . . Оn 1) В центре кольцевой батареи r = 0 и, следовательно, скорость фильтрации u здесь равна нулю. Таким образом, частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Эти точки фильтрационного поля называются точками равновесия. При разработке залежей нефти в окрестностях таких точек образуются «застойные области» . В условиях водонапорного режима 20 пласта в этих застойных областях могут возникнуть «целики нефти» .

Подсчет времени движения частицы несжимаемой жидкости вдоль линии тока Жидкость несжимаема 21

Время движения частицы жидкости вдоль линии тока (20)→ (19) z=x-iy - сопряженное с z комплексное переменное. Разделим переменные и интегрируем вдоль линии тока 22

Стягивание контура нефтеносности (КН) к эксплуатационной кольцевой батарее Время движения частиц КН по линиям тока Характеристическая функция (23) 23

( =const ), (23) → (22) Время движения по главной линии ( =0) Время движения по нейтральной линии ( = /n) Время начала обводнения tо (по главной линии) /из(24)/ Местоположение частицы контура нефтеносности на нейтральной линии тока r/ в момент прорыва воды в скважины /из (25)/ 24

Анализ уравнения (27): 1) Величина г'/а возрастает с увеличением отношения rн/a; 2) Чем больше величина радиуса первоначального контура нефтеносности, тем больше отставание точек контура нефтеносности, движущихся по нейтральной линии тока, от точек контура, движущихся по главной линии тока. 3) При величине радиуса контура нефтеносности гн ≥ 2 а можно пренебрегать членом уравнения (27) содержащим множитель а/гн и уравнение (27) можно записать в виде 4) Чем больше скважин в батарее, тем меньше отставание частиц контура нефтеносности от тех, которые движутся по главной линии тока, т. е. тем равномернее стягивается контур. 5) Формы контура нефтеносности, которая первоначально была в виде окружности, искажается лишь в ближайшей окрестности 25 скважин.

1) Общий объем добытой нефти за время безводной эксплуатации 2) Объем оставшейся в пласте нефти 3) Площадь ωн, занятая оставшейся в пласте нефтью в момент прорыва воды в скважины Вывод: при большом числе скважин в батарее нефтеносная площадь ωн не зависит от величины отношения а/гн. 26

Метод комформного отображения Функция F (z) комплексного переменного z = х +iy - поле некоторого плоского движения z = z (ς) Полученная из F функция F 1 определяет некоторый плоский фильтрационный поток на плоскости ς. Изучив первый поток F, можно изучить поток F 1 (ς). Задаваясь той или иной преобразующей функцией z = z (ς), из одного потока F (z) плоскости z можно получить бесчисленное множество других потоков на плоскости ς. Таким образом, функция z=z(ς) реализует конформное отображение плоскости z на плоскость ς. 27

Вывод некоторых формул для притока к скважинам при помощи конформного отображения Отделим в функции z=z(ς)действительную часть от мнимой Отсюда x=x(ξ, η), ξ= ξ(x, y), y=y(ξ, η), η= η(x, y). (2) В зависимости от того, однозначна или многозначна преобразующая функция z=z(ς), каждой точке плоскости ς соответствует одна или несколько точек плоскости z. Точно так же каждой линии одной плоскости соответствует одна или несколько линий на другой плоскости. Таким образом, линиям тока и эквипотенциалям, т. е. сетке течения одной плоскости, будет соответствовать вполне определенная сетка течения на другой плоскости. При этом сами значения потенциала скорости Ф и функции тока Ψ будут одинаковыми на соответствующих другу28 линиях обеих плоскостей.

Производная dz/dς - некоторая функция комплексного переменного, определенная в соответствующих другу точках обеих плоскостей z и ς. Т. е. предел отношения не зависит от закона стремления к нулю отрезков Δξ и Δη. Отсюда следует, что в каждой точке плоскости ς и соответствующей (или соответствующих) ей точке плоскости z отношение соответствующих бесконечно малых отрезков dz и dς, постоянно (3) Отсюда (4) Аргумент дроби равен разности аргументов числителя и знаменателя. argdz 1 — это угол между направлениями элемента dzl и осью х. Таким образом, arg dzl — arg dz 2 = arg dς1 — arg dς2, т. е. углы между отрезками dz 1, dz 2 и отрезками dς1, dς2 равны. Преобразование z(ς) или ς (z) называется конформным, так как оно сохраняет подобие бесконечно малых элементов в соответствующих 29 точках.

Приток к скважине Плоскость z - скважина радиусом гс. Плоскость ς - скважина радиусом с При конформном отображении дебиты скважин — стоков или источников — сохраняются на обеих плоскостях Доказательство l - произвольный замкнутый контур, окружающий скважину на плоскости z; λ - произвольный замкнутый контур, окружающий скважину на плоскости ς; dn и dl — элементы нормали и касательной для контура l на плоскости z; dv и d λ — элементы нормали и касательной для контура λ на плоскости ς. Абсолютная величина дебита | Q | скважины на плоскости z составляющая скорости фильтрации по нормали к контуру. 30

По смыслу конформного преобразования, сохраняющего подобие бесконечно малых элементов в соответствующих точках обеих плоскостей, согласно формуле (3) имеем (7)→(6) и сокращая на получим В правой части формулы (8) стоит абсолютная величина дебита скважины на плоскости ς, равная абсолютному значению дебита скважины на плоскости z. 31

Переход от плоско-параллельного к плоско-радиальному потоку методом комформных отображений - характеристическая функция плоско-параллельного потока (А — положительная и действительная постоянная). Отделяем действительную и мнимую части Отсюда Эквипотенциали φ = Ах = const - семейство прямых, параллельных оси у Линии тока ψ = Ау = const — прямые, параллельные оси х. (рис. ) Проекции скорости фильтрации Вывод. Характеристическая функция течения F (z) = Az определяет плоско-параллельное течение в сторону отрицательной оси х с постоянной во всех точках скоростью u =- А. 32

Замена переменного Сравниваем действительные и мнимые части Прямым линиям х = const плоскости z соответствуют на плоскости ς кривые ln =const, = const, т. е. окружности с центром в начале координат, а прямым у=const — лучи θ = const плоскости ς (рис. ). Сетке течения Ф = Ах = const, Ψ = Ay = const на плоскости z соответствует на плоскости ς сетка течения = const и θ = const, т. е. при А >0 приток к точечному стоку в начале координат с дебитом q = 2 А. 33

Приток к скважине в пласте с прямолинейным контуром питания Исходный поток - приток к точечному стоку на плоскости ς: Плоскость z: в точке х = 0, у = а находится скважина малого радиуса гс; ось х является эквипотенциалью φ=φк, а окружность малого радиуса гс — эквипотенциалью φ=φс; пласт полубесконечен; контур питания прямолинейный Цель задачи: найти преобразование ς = ς (z) или обратное z =z (ς), которое реализует конформное отображение верхней полуплоскости z в круг = к плоскости ς, а точку zc = ia плоскости z, где расположен центр скважины радиусом гс, в начало координат ς = 0 плоскости ς Рис. 7. Соответствие между плоскостями z и ς в задаче о притоке в скважину 34

Искомое преобразование: (11) Доказательство: 1) полагая z=ia, из формулы (11) получаем ς= 0, т. е. центру скважины на плоскости z соответствует начало координат ς= 0 на плоскости ς. 2) полагая в формуле (11) z = х — любому вещественному числу, имеем Откуда следует действительная ось z = х перешла в окружность ρн плоскости ς, а точка верхней полуплоскости z = ia в начало координат ς = 0. 35

Радиусы скважин обеих плоскостей связаны соотношением Из (11) Для комплексного потенциала на плоскости z получаем По формуле Дюпюи имеем Подставляем ρс из формулы (12) 36