Подходы в оценке тренда оценка тренда с

Подходы в оценке тренда • оценка тренда с помощью гладких функций f(t) – параметрические методы оценки тренда (методы аналитического выравнивания); • оценка тренда на основе различного рода скользящих средних – непараметрические методы (методы механического сглаживания). 1

Оценка тренда на основе функций • Подбор аналитической функции, удовлетворительно описывающей значение уровней ряда на всем интервале наблюдений. • Оценка тренда на основе функций f(t) выполняется как оценка параметров нелинейной регрессии , то есть зависимость исследуемого показателя mt от фактора времени. 2

Пример оценки тренда Пусть тренд имеет вид полиномиальной регрессионной зависимости: . Задача определения тренда по временному ряду x 1, x 2, …, xn сводится к оценке параметров a 0, a 1, …, ap. Применяем метод наименьших квадратов. 1) Минимизируем сумму квадратов отклонений между расчетными и фактическими значениями: (xt-a 0 -a 1 t-a 2 t 2 -…-aptp)2 min. 2) Для определения минимума, находим частные производные по aj (j=0, . . , p) и приравнивают их к нулю. Получаем систему из p+1 уравнений, разрешая которую получаем выражение для коэффициентов aj (j=0, …, p). 3

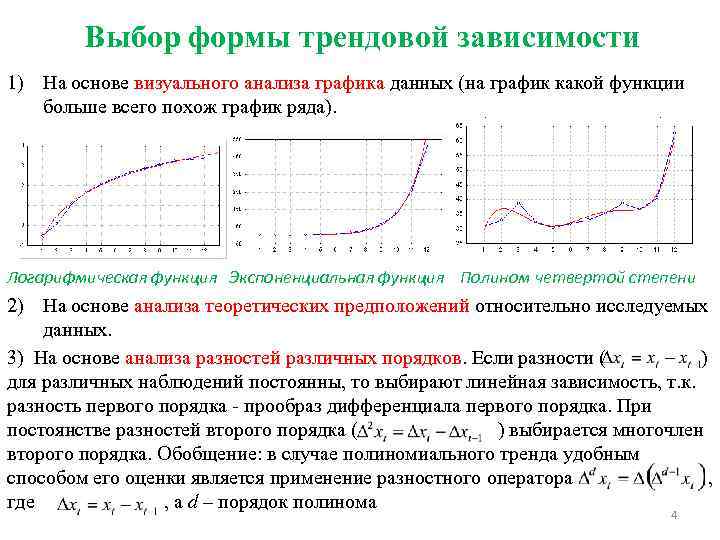Выбор формы трендовой зависимости 1) На основе визуального анализа графика данных (на график какой функции больше всего похож график ряда). Логарифмическая функция Экспоненциальная функция Полином четвертой степени 2) На основе анализа теоретических предположений относительно исследуемых данных. 3) На основе анализа разностей различных порядков. Если разности ( ) для различных наблюдений постоянны, то выбирают линейная зависимость, т. к. разность первого порядка - прообраз дифференциала первого порядка. При постоянстве разностей второго порядка ( ) выбирается многочлен второго порядка. Обобщение: в случае полиномиального тренда удобным способом его оценки является применение разностного оператора , где , а d – порядок полинома 4

Метод Скользящих средних Поскольку любая гладкая функция при самых общих допущениях может быть локально представлена полиномом с довольно высокой степенью точности, предпочтительной является следующая процедура. Подбираем полином к первой группе из 2 m+1 членов ряда и используем этот полином для определения значения тренда в m+1 -ой, средней точке группы. Затем подбираем полином того же порядка к группе, состоящей из второго, третьего, …, 2 m+2 наблюдения, и находим значение тренда в m+2 точке и так далее для всех членов ряда до последней группы из 2 m+1 членов. Эта процедура эквивалентна линейной комбинации наблюдений с коэффициентами, которые могут быть оценены раз и навсегда. Простейшее скользящее среднее можно вычислить по формуле: (1) Здесь 2 m+1– количество точек, на которых строится скользящее среднее. 5

Пример оценки тренда методом скользящих средних Подбираем полином третьего порядка к группам по семь точек. T = -3, -2, -1, 0, 1, 2, 3. Константы aj находим методом наименьших квадратов, то есть путём минимизации выражения: Дифференцируем выражение по aj, и выписываем уравнения при одинаковых степенях. Получаем систему: (2) 6

Пример оценки тренда методом скользящих средних В системе переносим в левую часть, а суммы с коэффициентами aj в правую часть, причем учитываем, что суммы нечетных порядков t от – 3 до 3 равны 0. (3) Для значения a 0, значения ряда в момент t=0, используем лишь первое и третье из уравнений, получаем: следовательно, значение тренда в какой-либо точке равно средневзвешенному значению семи точек с данной точкой в качестве центральной и весами , или в силу симметричности . 7

Пример оценки тренда методом скользящих средних Рассмотрим конкретный ряд t= 1 2 xt= 0 1 3 8 4 5 6 7 8 9 27 64 125 216 343 512 Значение тренда в точке 4 (t=4) будет: и оно совпадает с соответствующим членом ряда. 8

Общая процедура оценки тренда методом скользящих средних Если к 2 m+1 точкам подбирают полином порядка p, необходимо минимизировать: Минимизация приводит к уравнениям, аналогичным (2), которые разбиваются на две подсистемы, подобные (3). Решение относительно a 0 зависит от численных значений суммы t j и линейных функций от xt типа t j xt. Далее значение тренда в точке t=k вычисляется как взвешенное среднее значение от xk-m до xk+m. 9

Свойства весов 1. Сумма весов равна единице. Это следует из того, что если применить процедуру взвешивания к ряду, все члены которого равны одной и той же константе, то среднее должно равняться этой же константе; 2. Веса симметричны относительно серединного значения. Это следует из того, что они получены, как функции сумм t j xt, которые сами симметричны; 3. Значения тренда не зависят от направления отсчета времени, в силу свойства 2); 4. Для полиномов четного порядка (2 k) формулы будут те же самые, что и для полиномов нечетного порядка (2 k+1); 10

Неудобства применения метода скользящих средних 1. Формулы не позволяют вычислить значения тренда для первых и последних m значений ряда; Наличие краевого эффекта. 2. Можно вывести формулу для построения тренда на четном числе точек, однако, при этом значения тренда были бы получены в серединах временных интервалов между наблюдениями. 3. Выделение тренда методом скользящих средних может «исказить» сезонную компоненту 11

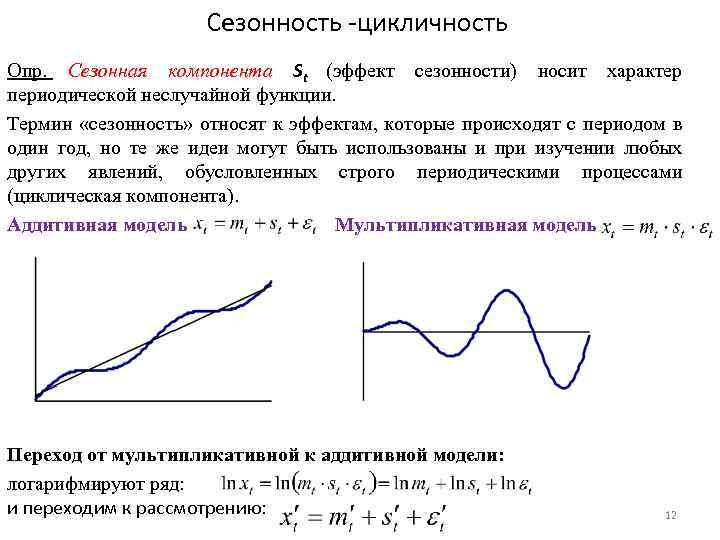Сезонность -цикличность Опр. Сезонная компонента St (эффект сезонности) носит характер периодической неслучайной функции. Термин «сезонность» относят к эффектам, которые происходят с периодом в один год, но те же идеи могут быть использованы и при изучении любых других явлений, обусловленных строго периодическими процессами (циклическая компонента). Аддитивная модель Мультипликативная модель Переход от мультипликативной к аддитивной модели: логарифмируют ряд: и переходим к рассмотрению: 12

Определение наличия сезонной компоненты Определения наличия периодической компоненты на основе: • Визуального анализа графика исходных данных; • Теоретических предпосылках о наличии сезонности (цикличности); • Спектрального анализа; • Анализа коррелограмм АКФ и ЧАКФ; . 13

Определение тренда и сезонности на основе коррелограмм Сезонность (период 12) Наличие тренда 14

Подходы в оценке сезонной компоненты • оценка сезонной компоненты с помощью оценка с помощью тригонометрических функций (метод гармоник); • оценка сезонной компоненты методом сезонных поправок (или индексов) • оценка сезонной компоненты с помощью введения фиктивных переменных 15

Оценка сезонной компоненты с помощью тригонометрических функций Определение. Пару называют гармоникой с периодом T. В общем случае сезонную компоненту можно оценить с помощью суммы тригонометрических функций. На практике сезонную компоненту обычно представляют в виде одной гармонической пары: Коэффициенты a, b и c определяют методом наименьших квадратов. Оценка сезонной компоненты таким образом – построение нелинейной регрессии по времени, где в качестве аналитических функций – Sin и Cos. 16

Качество оценки сезонной компоненты Не всегда результат, полученный с помощью одной только гармонической пары, является удовлетворительным. Поэтому иногда приходится брать две, три и т. д. гармонических пар соответственно с периодами , и т. д. Качество оценки сезонной компоненты контролируют по близости индекса детерминации к 1 или, исходя из минимума значений информационных критериев. Если при введении дополнительной гармонической пары для оценки сезонной компоненты изменяет индекс детерминации R 2 не более, чем на 0, 03, то добавление этой пары было нецелесообразно. 17

Совместная оценка сезонности и цикличности Если сезонный эффект присутствует в структуре ряда St и его период равен T 1, а также присутствует эффект циклических повторений Vt с периодом T 2, то совместную оценку сезонности и цикличности можно проводить на основе модели (аддитивной): 18

Метод сезонных индексов для аддитивной модели Аддитивная модель временного ряда: xt=mt+st+εt. Пусть тренд линейный mt=a+bt, коэффициенты и оцениваются методом наименьших квадратов по всем n наблюдениям. Период сезонности равен T. Тогда временной ряд описывается моделью следующего вида: где st - сезонный индекс, определяется как среднее арифметическое значение , соответствующих фаз колебаний: Здесь N – целая часть от деления количества наблюдений на период колебаний (N=[n/T]). 19

Метод сезонных индексов для мультипликативной модели Мультипликативная модель временного ряда с линейным трендом: где ft - мультипликативный сезонный индекс, определяется как среднее арифметическое значение соответствующих фаз колебаний При мультипликативной модели применять метод сезонных индексов можно только в случае, когда N 5. Метод сезонных поправок можно обобщить на случай нелинейного тренда F(t), тогда аддитивная модель будет иметь вид: мультипликативная модель: В этих моделях сначала оценивают параметры нелинейного тренда F(t), затем проводят процедуру оценки индексов st и ft аналогично случаю линейного тренда. 20

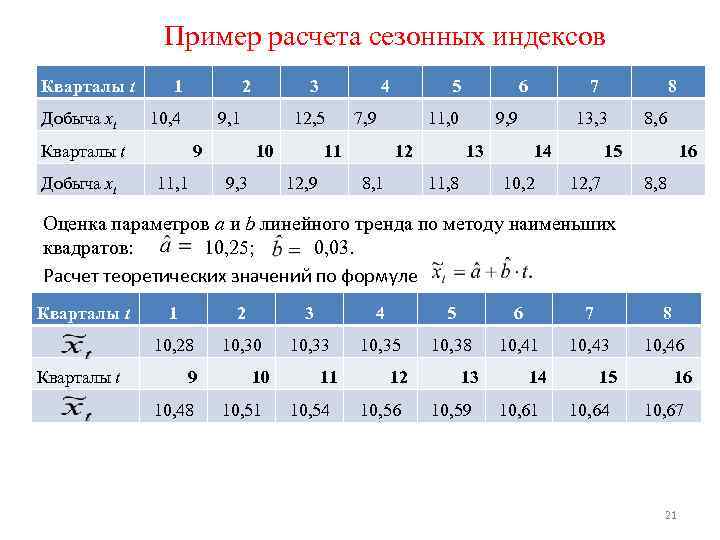Пример расчета сезонных индексов Кварталы t Добыча xt 1 2 10, 4 9, 1 Кварталы t Добыча xt 3 9 11, 1 4 12, 5 10 9, 3 7, 9 11 12, 9 5 6 11, 0 12 8, 1 7 9, 9 13 11, 8 8 13, 3 14 10, 2 8, 6 15 12, 7 16 8, 8 Оценка параметров a и b линейного тренда по методу наименьших квадратов: 10, 25; 0, 03. Расчет теоретических значений по формуле Кварталы t 2 3 4 5 6 7 8 10, 28 Кварталы t 1 10, 30 10, 33 10, 35 10, 38 10, 41 10, 43 10, 46 9 10, 48 10 10, 51 11 10, 54 12 10, 56 13 10, 59 14 10, 61 15 10, 64 16 10, 67 21

Пример расчета сезонных индексов Находят отношения фактических значений к теоретическим Кварталы t 2 3 4 5 6 7 8 1, 012 Кварталы t 1 0, 883 1, 210 0, 763 1, 060 0, 951 1, 275 0, 822 9 1, 059 10 0, 885 11 1, 224 12 0, 767 13 1, 114 14 0, 961 15 1, 194 16 0, 825 22

Стохастический дискретный процесс Рассмотрим последовательность случайных переменных , каждая из которых имеет одно единственное возможное значение соответственно Такая последовательность называется дискретным стохастическим процессом . Для такого процесса математическое ожидание может изменяться во времени Аналогично дисперсия также может изменяться во времени Автоковариация в общем виде зависит от каждого и. Определение: Конечная реализация дискретного стохастического процесса называется временным рядом.

Понятие стационарности. Опр. 1 (строгой стационарности или стационарности в узком смысле) Случайный (стохастический) процесс является строго стационарным, если сдвиг во времени не меняет и одну из функций плотности распределения. То есть, если ко всем моментам времени прибавить некую целочисленную величину, то функция плотности при этом не изменится: для всех n, моментов времени и целочисленном Δ. Опр. 2 (слабой стационарности или стационарности в широком смысле) Случайный процесс называются стационарным в широком смысле, если он обладает постоянной средней и дисперсией (то есть дисперсия и математическое ожидание не зависят от времени), а ковариация зависит только от временного интервала между двумя отдельными наблюдениями. То есть случайный процесс vt называют стационарным, если для него выполняются следующие условия: 1) М(vt)= М(vt+k)=m=const; 2) D( t)= 2=const; 3) cov(vi, vj)=cov(vi+l, vj+l) при любых i j. Соответственно временные ряды представленные строго стационарными и слабо стационарными 24 случайными процессами называются стационарными временными рядами в узком и широком смысле.

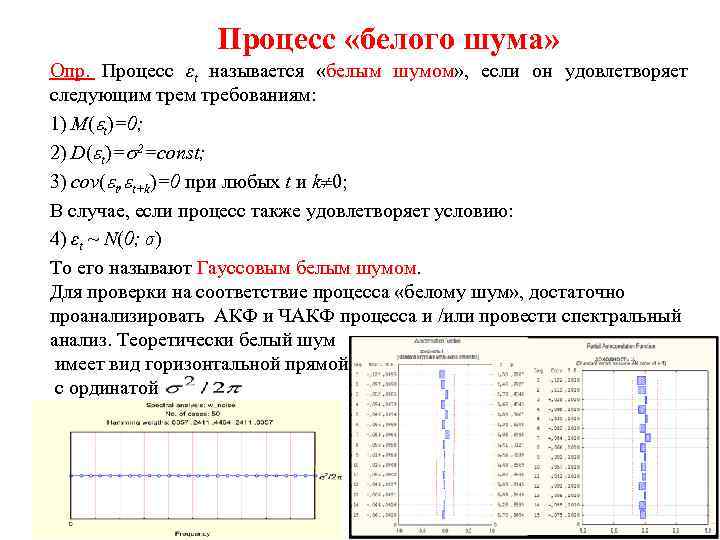Процесс «белого шума» Опр. Процесс εt называется «белым шумом» , если он удовлетворяет следующим требованиям: 1) М( t)=0; 2) D( t)= 2=const; 3) cov( t, t+k)=0 при любых t и k 0; В случае, если процесс также удовлетворяет условию: 4) εt ~ N(0; σ) То его называют Гауссовым белым шумом. Для проверки на соответствие процесса «белому шум» , достаточно проанализировать АКФ и ЧАКФ процесса и /или провести спектральный анализ. Теоретически белый шум имеет вид горизонтальной прямой с ординатой 25

Модели скользящей средней Опр. 4. Модель скользящей средней (Moving Average) – это модель, где моделируемая величина задается линейной комбинацией от процессов белого шума, следующими друг за другом (3) Где q – количество лагов запаздывания называется порядком МА-модели. Термин «скользящая средняя» , используемый здесь не стоит путать с соответствующим термином, относящимся к непараметрическим методом поиска тренда. Процессы скользящей средней – всегда стационарны в слабом смысле. Введем понятие оператора сдвига: Тогда процесс МА(q) можно записать как 26

Авторегрессионные процессы Опр. 3. Авторегресонным (Auto-Regressive) называется процесс, при котором значение ряда находится в линейной зависимости от предыдущих значений. Например, если текущее наблюдаемое значение является функцией всего лишь одного значения, непосредственно предшествующего наблюдению, то есть процесс зависит всего лишь от одного значения рассматриваемой переменной, то процесс называется авторегрссионным процессом первого порядка и обозначается AR(1). Это можно обобщить следующим образом: если анализируемый динамический процесс зависит от 1 до p временных лагов назад, то это авторегрессионный процесс порядка р, т. е. AR(р): (1) Здесь текущее значение Y – функция от р наиболее недавних предыдущих значений. р– порядок авторегрессии. - процесс белого шума 27

Авторегрессионные модели скользящей средней (АРСС) ОПР. Модели временных рядов, которые сочетают авторегрессионный процесс с моделью скользящей средней называются авторегрессионными моделями скользящей средней (АРСС, ARMA). Модель АРСС(p, q) имеет р временных лагов в авторегрессионном процессе и q интервалов в модели скользящей средней. (4) где - остаточный член ошибки – белый шум. Так АРСС(3, 2) имеет вид: АRМА процесс моет быть представлен при самых общих допущениях как бесконечный AR-процесс или как бесконечный МА-процесс. При анализе временных рядов рекомендуется выбирать конечные АРССпроцессы с наименьшим числом параметров, подлежащих оценке Как правило . 28

Идентификация модели АРСС Опр. Пусть дана модель АРСС(p, q) для временного ряда Yt . Идентификацией этой модели называется процедура определения неизвестных значений p и q. Существует несколько подходов к идентификации моделей АРСС. I подход: Идентификацию модели АРСС проводят на визуальном анализе коррелограммы АКФ и частичной коррелограммы ЧАКФ. Здесь используются следующие особенности АКФ: • В случае АР моделей ее модуль убывает по экспоненте, осциллируя около нуля; • В случае СС(q) модели только первые q значений отличны от нуля; • В модели АРСС(p, q), после q-р значений, АКФ имеет вид, такой же, как АР модель. Свойства поведения ЧАКФ: • Для АР(р) моделей, она равна нулю после первых р значений. • Для моделей СС она экспоненциально убывает по модулю. • Для АРСС(р, q) моделей, после первых р-q значений, она ведет себя также как и для модели СС. 29

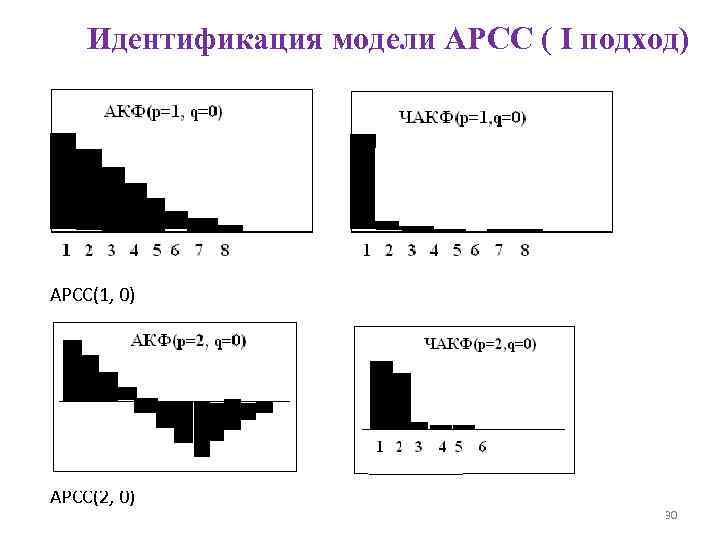Идентификация модели АРСС ( I подход) АРСС(1, 0) АРСС(2, 0) 30

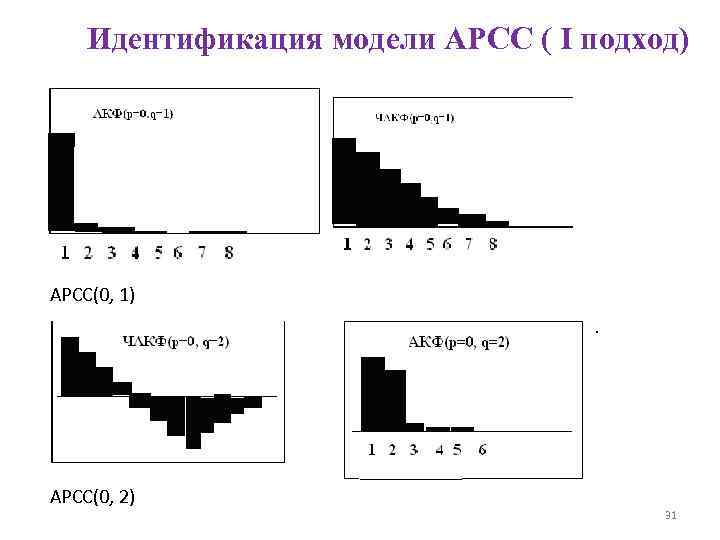Идентификация модели АРСС ( I подход) АРСС(0, 1) АРСС(0, 2) 31

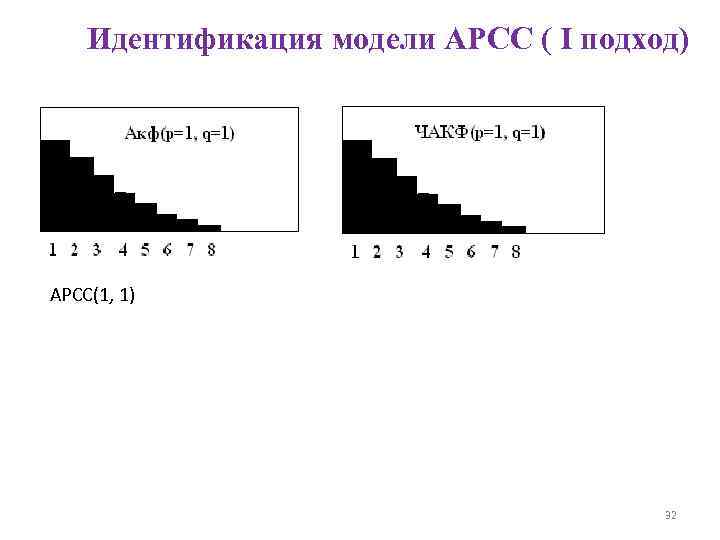Идентификация модели АРСС ( I подход) АРСС(1, 1) 32

Проверка адекватности модели АРСС Для проверки адекватности модели АРСС, заключающейся в тестировании оценок на достоверность (эффективность, состоятельность и несмещенность) необходимо проанализировать остатки έ. Если модель АРСС (p; q)достаточно хорошо описана, то остатки являются независимыми нормально распределенными случайными величинами с нулевым математическим ожиданием, с постоянной дисперсией и нулевой атокорреляцией. Поэтому для проверки адекватности модели (достоверности оцененных параметров) достаточно проверить остаточную компоненту на соответствии гауссову «белому шуму» . Для этого проводят спектральный анализ или анализ АКФ, ЧАКФ + тест на нормальность (Пирсона, Колмогорова-Смирнова, Бера. Жарка).

Прогнозирование на основе анализа временных рядов 1. Постановка задачи, подбор исходной информации. 2. Предварительный анализ исходных временных рядов и формирование набора моделей прогнозирования. 3. Численное оценивание параметров моделей. 4. Определение адекватности моделей. 5. Селекция моделей прогнозирования: Выбор наилучшей или построение обобщающей модели. 6. Вычисление прогноза и нахождение его доверительного интервала. 7. Содержательный анализ полученного прогноза. 8. Сверка прогноза по контрольной выборке 9. Коррекция прогноза при необходимости 10. Сдача прогнозной модели в эксплуатацию. 34

Прогнозирование тренда При прогнозирование на основе компонентного анализа каждая компонента прогнозируется в отдельности, полученные прогнозные значения складываются (таим образом получается прогноз по аддитивной модели) и при необходимости потенцируются (таим образом получается прогноз по аддитивной модели, если первоначальные данные были прологарифмированы) В случае, когда тренд описывался с помощью аналитических функций, достаточно в формулу, выражающую зависимость тренда от времени, подставить период упреждения прогноза. Пример: На основе квартальных данных о прибыли компании за 5 лет построена тренд-сезонная модель - линейный тренд (t=1, 2, …, 20) Найти прогноз тренда на будущий квартал. Для решения необходимо подставить в формулу тренда значение t=21: 35

Прогнозирование сезонной компоненты 1. В случае, когда сезонная компонента оценивалась с помощью тригонометрических функций, процедура построения прогноза достаточна проста. В формулу для определения сезонной компоненты подставляют период упреждения прогноза t, и рассчитывают соответствующее значение сезонной составляющей. Например, чтобы узнать значения сезонной компоненты для t=12 в формулу подставляют оцененные коэффициенты период колебаний T=4 и время t=12. В итоге получают: 2. В случае, когда сезонная компонента оценивалась методом сезонных индексов, в качестве прогнозных оценок St берутся сами скорректированные теоретические значения. 3. В случае оценки сезонной компоненты методом фиктивных переменных рассчитывают прогнозные значения компоненты для каждой фазы цикла, как прогнозные значения многофакторной регрессии, где в качестве факторов используются фиктивные переменные. 36

Прогнозирование по модели АРСС. Пусть дан случайный процесс, описываемый моделью АРСС(p, q): Найдем прогнозное значение этого процесса в момент времени (t+l) по известным значениям (здесь l является периодом упреждения прогноза). Тогда выражается следующим образом: В правой части выражения могут присутствовать как неизвестные значения (1

Доверительный интервал в прогнозах Вопрос надежности прогнозов сводится к проблеме построения доверительных интервалов прогнозов. Построение доверительных интервалов осуществляется на основе ошибок ретроспективных прогнозов, выполненных на один шаг вперед lt=xtxt-1, и опирается на оценку дисперсии ошибки прогноза , которая оценивается по формуле: Здесь Т – период ретроспективы ряда. Нижняя и верхняя границы интервалов определяются соответственно путем вычитания из прогнозной оценки модели x. T(τ) и сложения с ней величины R(τ), , где – среднеквадратичное отклонение ошибки прогноза, –t-статистика Стьюдента с вероятностью p и степенью свободы n, Zk( ) – точечный прогноз на шагов вперед. Ширина доверительного интервала зависит от периода упреждения прогноза и от средней квадратической ошибки , характеризующей качество модели на ретроспективном участке прогнозирования =1. То есть доверительный интервал прогноза имеет вид (xt( )-R( ); xt( )+R( )). xt( )-R( ) – пессимистичный прогноз xt( )+R( ) – оптимистичный прогноз 38