ПОДБОР ПАРАМЕТРОВ. ПОИСК ОПТИМАЛЬНЫХ РЕШЕНИЙ Команда























lektsia_9.ppt
- Размер: 547.0 Кб
- Автор:
- Количество слайдов: 30
Описание презентации ПОДБОР ПАРАМЕТРОВ. ПОИСК ОПТИМАЛЬНЫХ РЕШЕНИЙ Команда по слайдам
 ПОДБОР ПАРАМЕТРОВ. ПОИСК ОПТИМАЛЬНЫХ РЕШЕНИЙ
ПОДБОР ПАРАМЕТРОВ. ПОИСК ОПТИМАЛЬНЫХ РЕШЕНИЙ
 Команда Подбор параметра меню Сервис позволяет определить неизвестное значение (параметр), которое будет давать желаемый результат. Технология использования команды следующая: • решить нужную задачу с каким-либо начальным значением параметра; • выбрать команду Подбор параметра меню Сервис ; • в окне диалога Подбор параметра в поле Установить в ячейке задать абсолютную ссылку на ячейку, содержащую расчетную формулу, а в поле Значение — то значение, которое следует получить в качестве результата формулы; • в поле Изменяя значение яче йки ввести ссылку на ячейку с параметром; • нажать кнопку ОК или клавишу Enter , на экране появится окно диалога Результат подбора параметра; • для сохранения найденного значения нажать кнопку ОК. Для восстановления значения, которое было в ячейке с параметром до использования команды Подбор параметра нажать кнопку Отмена.
Команда Подбор параметра меню Сервис позволяет определить неизвестное значение (параметр), которое будет давать желаемый результат. Технология использования команды следующая: • решить нужную задачу с каким-либо начальным значением параметра; • выбрать команду Подбор параметра меню Сервис ; • в окне диалога Подбор параметра в поле Установить в ячейке задать абсолютную ссылку на ячейку, содержащую расчетную формулу, а в поле Значение — то значение, которое следует получить в качестве результата формулы; • в поле Изменяя значение яче йки ввести ссылку на ячейку с параметром; • нажать кнопку ОК или клавишу Enter , на экране появится окно диалога Результат подбора параметра; • для сохранения найденного значения нажать кнопку ОК. Для восстановления значения, которое было в ячейке с параметром до использования команды Подбор параметра нажать кнопку Отмена.
 • При подборе параметра Excel использует итерационный процесс. Он проверяет для изменяемой ячейки одно значение за другим, пока не получит нужное решение. • Если задача подбора параметра занимает много времени, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг , чтобы просмотреть результаты последовательных итераций. • По умолчанию команда Подбор параметра прекращает вычисления, когда выполняется 100 итераций, или при получении результата, который находится в пределах 0, 001 от заданного целевого значения. Если нужна большая точность, можно изменить используемые по умолчанию параметры на вкладке Вычисления команды Параметры меню Сервис. • Команда Подбор параметра находит только одно решение, даже если задача имеет несколько решений.
• При подборе параметра Excel использует итерационный процесс. Он проверяет для изменяемой ячейки одно значение за другим, пока не получит нужное решение. • Если задача подбора параметра занимает много времени, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг , чтобы просмотреть результаты последовательных итераций. • По умолчанию команда Подбор параметра прекращает вычисления, когда выполняется 100 итераций, или при получении результата, который находится в пределах 0, 001 от заданного целевого значения. Если нужна большая точность, можно изменить используемые по умолчанию параметры на вкладке Вычисления команды Параметры меню Сервис. • Команда Подбор параметра находит только одно решение, даже если задача имеет несколько решений.
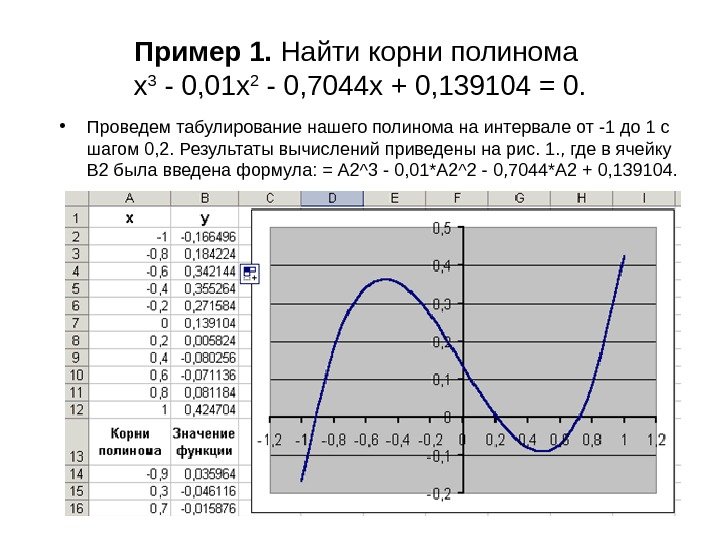
 Пример 1. Найти корни полинома x 3 — 0, 01 x 2 — 0, 7044 x + 0, 139104 = 0. • Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0, 2. Результаты вычислений приведены на рис. 1. , где в ячейку В 2 была введена формула: = A 2^3 — 0, 01*A 2^2 — 0, 7044*A 2 + 0, 139104.
Пример 1. Найти корни полинома x 3 — 0, 01 x 2 — 0, 7044 x + 0, 139104 = 0. • Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0, 2. Результаты вычислений приведены на рис. 1. , где в ячейку В 2 была введена формула: = A 2^3 — 0, 01*A 2^2 — 0, 7044*A 2 + 0, 139104.
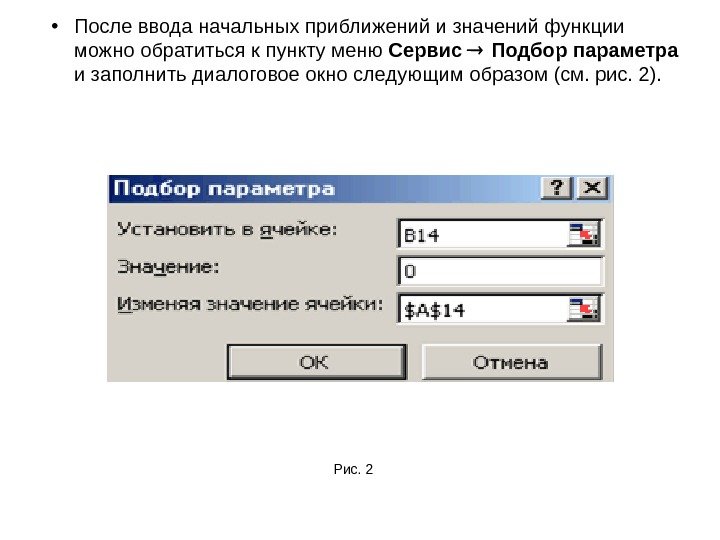
 • После ввода начальных приближений и значений функции можно обратиться к пункту меню Сервис Подбор параметра и заполнить диалоговое окно следующим образом (см. рис. 2). Рис.
• После ввода начальных приближений и значений функции можно обратиться к пункту меню Сервис Подбор параметра и заполнить диалоговое окно следующим образом (см. рис. 2). Рис.
 • После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра (см. рис. 3) с сообщением об успешном завершении поиска решения, приближенное значение корня будет помещено в ячейку А 14. Рис.
• После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра (см. рис. 3) с сообщением об успешном завершении поиска решения, приближенное значение корня будет помещено в ячейку А 14. Рис.
 • Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А 15 и А 16 (см. рис. 4). Р ис.
• Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А 15 и А 16 (см. рис. 4). Р ис.
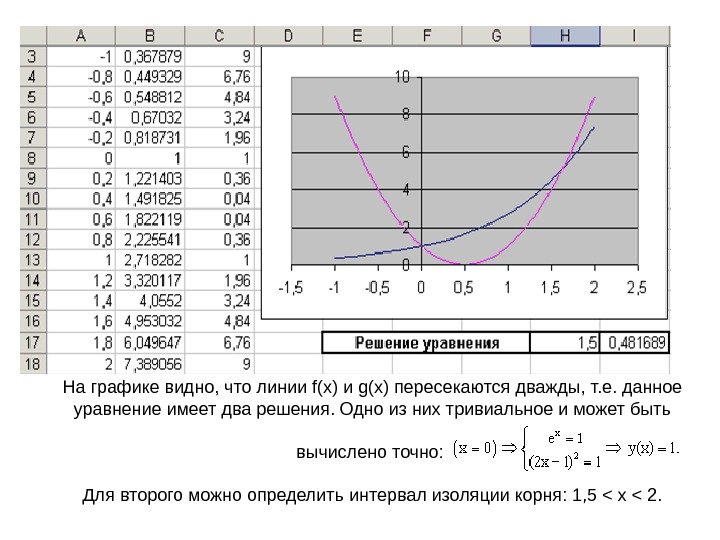
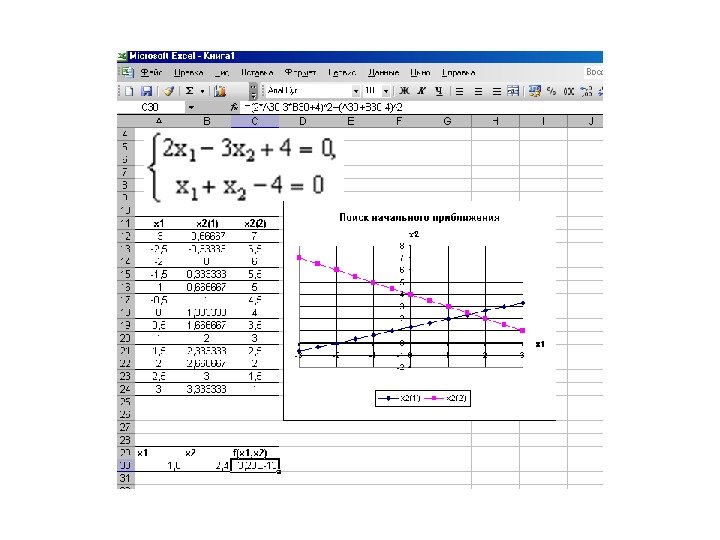
 Пример 2. Решить уравнение e x — (2 x — 1) 2 = 0. Проведем локализацию корней нелинейного уравнения. Для этого представим его в виде f(x) = g(x) , т. е. ex = (2 x — 1)2 или f(x) = ex , g(x) = (2 x — 1) 2 , и решим графически. Графическим решением уравнения f(x) = g(x) будет точка пересечения линий f(x) и g(x).
Пример 2. Решить уравнение e x — (2 x — 1) 2 = 0. Проведем локализацию корней нелинейного уравнения. Для этого представим его в виде f(x) = g(x) , т. е. ex = (2 x — 1)2 или f(x) = ex , g(x) = (2 x — 1) 2 , и решим графически. Графическим решением уравнения f(x) = g(x) будет точка пересечения линий f(x) и g(x).
 На графике видно, что линии f(x) и g(x) пересекаются дважды, т. е. данное уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно: Для второго можно определить интервал изоляции корня: 1, 5 < x < 2.
На графике видно, что линии f(x) и g(x) пересекаются дважды, т. е. данное уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно: Для второго можно определить интервал изоляции корня: 1, 5 < x < 2.
![• Теперь можно найти корень уравнения на отрезке [1. 5, 2] методом последовательных приближений. • Теперь можно найти корень уравнения на отрезке [1. 5, 2] методом последовательных приближений.](http://present5.com/presentforday2/20161111/lektsia_9.ppt_images/lektsia_9.ppt_9.jpg) • Теперь можно найти корень уравнения на отрезке [1. 5, 2] методом последовательных приближений. • Введём начальное приближение в ячейку Н 17 = 1, 5, и само уравнение, со ссылкой на начальное приближение, в ячейку I 17 =EXP(H 17)-(2*H 17 -1)^2 (см. рис. 5).
• Теперь можно найти корень уравнения на отрезке [1. 5, 2] методом последовательных приближений. • Введём начальное приближение в ячейку Н 17 = 1, 5, и само уравнение, со ссылкой на начальное приближение, в ячейку I 17 =EXP(H 17)-(2*H 17 -1)^2 (см. рис. 5).
 Далее воспользуемся пунктом меню Сервис Подбор параметра и заполним диалоговое окно Подбор параметра (см. рис. 6). Рис. 6 Результат поиска решения будет выведен в ячейку Н 17 (см. рис. 7). Ри с.
Далее воспользуемся пунктом меню Сервис Подбор параметра и заполним диалоговое окно Подбор параметра (см. рис. 6). Рис. 6 Результат поиска решения будет выведен в ячейку Н 17 (см. рис. 7). Ри с.
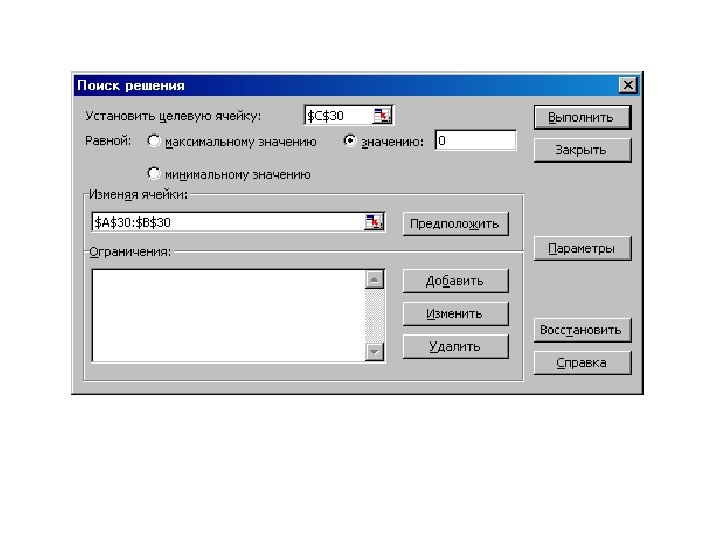
 Поиск решений • Поиск решений может применяться для решения задач, которые включают много изменяемых ячеек, и помогает найти комбинацию переменных, которые максимизируют или минимизируют значение в целевой ячейке. • Он также позволяет задать одно или несколько ограничений условий, которые должны выполняться при поиске решений. • Для запуска этого инструмента следует выполнить команду Поиск решения меню Сервис.
Поиск решений • Поиск решений может применяться для решения задач, которые включают много изменяемых ячеек, и помогает найти комбинацию переменных, которые максимизируют или минимизируют значение в целевой ячейке. • Он также позволяет задать одно или несколько ограничений условий, которые должны выполняться при поиске решений. • Для запуска этого инструмента следует выполнить команду Поиск решения меню Сервис.
 • В диалоговом окне Поиск решения в поле Установить целевую ячейку задается цель, которую должен достичь поиск решения. • Целевая ячейка может быть задана ссылкой или именем. Поиск решения может находить конкретное значение целевой функции. • В этом случае, задав только изменяемую ячейку без указания ограничений, можно использовать Поиск решения вместо команды Подбор параметра.
• В диалоговом окне Поиск решения в поле Установить целевую ячейку задается цель, которую должен достичь поиск решения. • Целевая ячейка может быть задана ссылкой или именем. Поиск решения может находить конкретное значение целевой функции. • В этом случае, задав только изменяемую ячейку без указания ограничений, можно использовать Поиск решения вместо команды Подбор параметра.
 • Цель поиска решений может не задаваться. Тогда поле Установить целевую ячейку следует оставить пустым, нажать кнопку Параметры и установить флажок Показывать результаты итераций. • Поиск решения будет перебирать комбинации изменяемых ячеек, которые удовлетворяют заданным ограничениям. • Пользователь может выбрать нужное решение, но оно необязательно будет оптимальным.
• Цель поиска решений может не задаваться. Тогда поле Установить целевую ячейку следует оставить пустым, нажать кнопку Параметры и установить флажок Показывать результаты итераций. • Поиск решения будет перебирать комбинации изменяемых ячеек, которые удовлетворяют заданным ограничениям. • Пользователь может выбрать нужное решение, но оно необязательно будет оптимальным.
 • В поле Изменяя ячейки следует задать ячейки с переменными. Можно указать ссылки на ячейки или их имена. • Если ячейки находятся в несмежных диапазонах, их следует разделять точкой с запятой. • Вместо ввода ячеек можно нажать кнопку Предположить , и поиск решения сам предложит изменяемые ячейки, исходя из заданной целевой функции. Поле Изменяя ячейки нельзя оставить пустым, и указанные в нем ячейки обязательно должны влиять на значение целевой ячейки.
• В поле Изменяя ячейки следует задать ячейки с переменными. Можно указать ссылки на ячейки или их имена. • Если ячейки находятся в несмежных диапазонах, их следует разделять точкой с запятой. • Вместо ввода ячеек можно нажать кнопку Предположить , и поиск решения сам предложит изменяемые ячейки, исходя из заданной целевой функции. Поле Изменяя ячейки нельзя оставить пустым, и указанные в нем ячейки обязательно должны влиять на значение целевой ячейки.
 • Последний шаг определения поиска решений — задание ограничений. Он не является обязательным. Чтобы задать ограничения, следует в окне Поиск решения нажать кнопку Добавить и заполнить окно диалога Добавление ограничений. • Ограничение состоит из трех компонентов: 1. ссылки на ячейку, 2. оператора сравнения 3. значения ограничения. • В левой части от оператора сравнения кроме ссылки на ячейку может также задаваться ссылка на диапазон. В правой части может задаваться диапазон (той же размерности, что и в левой части), ссылка на ячейку или константное значение.
• Последний шаг определения поиска решений — задание ограничений. Он не является обязательным. Чтобы задать ограничения, следует в окне Поиск решения нажать кнопку Добавить и заполнить окно диалога Добавление ограничений. • Ограничение состоит из трех компонентов: 1. ссылки на ячейку, 2. оператора сравнения 3. значения ограничения. • В левой части от оператора сравнения кроме ссылки на ячейку может также задаваться ссылка на диапазон. В правой части может задаваться диапазон (той же размерности, что и в левой части), ссылка на ячейку или константное значение.
 Пример 3. Решить систему уравнений: Рассмотрим, как можно решить систему уравнений: F 1 (x)=0, F 2 (x)=0, … F n (x)=0 Для решения этой задачи ее можно сформулировать одним из следующих способов: 1. Найти минимум (максимум) функции при системе ограничений, заданной в виде равенств F i (x) = 0; 2. Найти минимум функции В этом случае задача решается без ограничений.
Пример 3. Решить систему уравнений: Рассмотрим, как можно решить систему уравнений: F 1 (x)=0, F 2 (x)=0, … F n (x)=0 Для решения этой задачи ее можно сформулировать одним из следующих способов: 1. Найти минимум (максимум) функции при системе ограничений, заданной в виде равенств F i (x) = 0; 2. Найти минимум функции В этом случае задача решается без ограничений.

 =(2*A 30 -3*B 30+4)^2+(A 30+B 30 -4)^
=(2*A 30 -3*B 30+4)^2+(A 30+B 30 -4)^


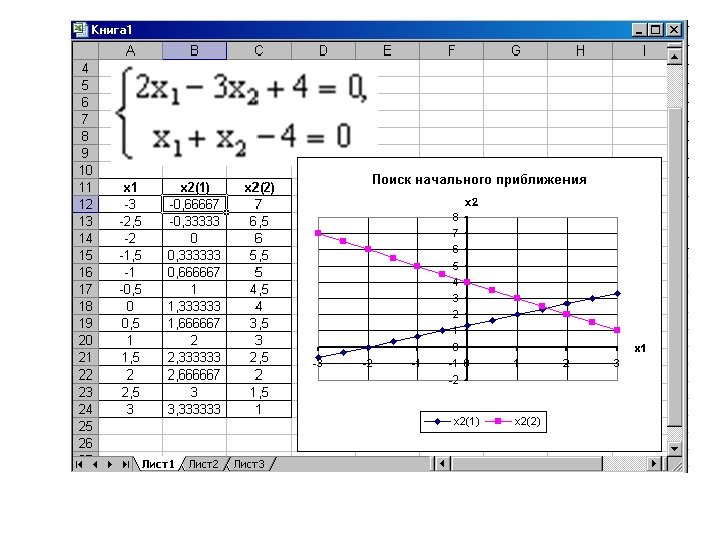
 1 -й способ. • В ячейки А 1 и А 2 вводим числа 0 (здесь мы будем хранить x 1 и x 2 ). • В ячейки В 1 и В 2 вводим ограничения: В 1 = 2*А 1 -3*А 2, В 2 = А 1+А 2. • В ячейку С 1 введем функцию цели (эту ячейку мы будем минимизировать): С 1 = СУММ(B 1: B 2). Рис. 8 Воспользуемся командой Сервис Поиск Решения и заполним появившееся диалоговое окно так, как показано на рис. 8. В результате решения поставленной задачи получим решение системы исходных уравнений: x 1 = 1, 6, x 2 = 2, 4.
1 -й способ. • В ячейки А 1 и А 2 вводим числа 0 (здесь мы будем хранить x 1 и x 2 ). • В ячейки В 1 и В 2 вводим ограничения: В 1 = 2*А 1 -3*А 2, В 2 = А 1+А 2. • В ячейку С 1 введем функцию цели (эту ячейку мы будем минимизировать): С 1 = СУММ(B 1: B 2). Рис. 8 Воспользуемся командой Сервис Поиск Решения и заполним появившееся диалоговое окно так, как показано на рис. 8. В результате решения поставленной задачи получим решение системы исходных уравнений: x 1 = 1, 6, x 2 = 2, 4.
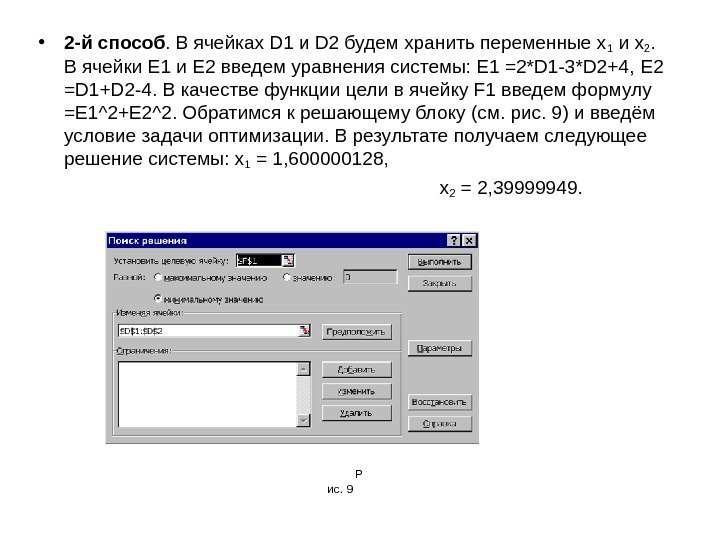
 • 2 -й способ. В ячейках D 1 и D 2 будем хранить переменные x 1 и x 2. В ячейки E 1 и E 2 введем уравнения системы: E 1 =2*D 1 -3*D 2+4, E 2 =D 1+D 2 -4. В качестве функции цели в ячейку F 1 введем формулу =E 1^2+E 2^2. Обратимся к решающему блоку (см. рис. 9) и введём условие задачи оптимизации. В результате получаем следующее решение системы: x 1 = 1, 600000128, x 2 = 2, 39999949. Р ис.
• 2 -й способ. В ячейках D 1 и D 2 будем хранить переменные x 1 и x 2. В ячейки E 1 и E 2 введем уравнения системы: E 1 =2*D 1 -3*D 2+4, E 2 =D 1+D 2 -4. В качестве функции цели в ячейку F 1 введем формулу =E 1^2+E 2^2. Обратимся к решающему блоку (см. рис. 9) и введём условие задачи оптимизации. В результате получаем следующее решение системы: x 1 = 1, 600000128, x 2 = 2, 39999949. Р ис.
![Если функция f ( x ) непрерывна на отрезке [ a , b ] Если функция f ( x ) непрерывна на отрезке [ a , b ]](http://present5.com/presentforday2/20161111/lektsia_9.ppt_images/lektsia_9.ppt_23.jpg) Если функция f ( x ) непрерывна на отрезке [ a , b ] и известна ее первообразная F ( x ), то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона-Лейбница )()()(a. Fb. Fdxxf b a где )()(xfx.
Если функция f ( x ) непрерывна на отрезке [ a , b ] и известна ее первообразная F ( x ), то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона-Лейбница )()()(a. Fb. Fdxxf b a где )()(xfx.
 Формула трапеций Величина определенного интеграла численно равна площади криволинейной трапеции, ограниченной частью графика y = f ( x ), осью x и линиями x = a , x = b , т. е. S fxdx. S a b () 4321 )(SSSSSdxxf b a
Формула трапеций Величина определенного интеграла численно равна площади криволинейной трапеции, ограниченной частью графика y = f ( x ), осью x и линиями x = a , x = b , т. е. S fxdx. S a b () 4321 )(SSSSSdxxf b a
 Формула трапецийh hafaf S 2 )()( 1 h bfhaf h hafhaf h hafaf S 2 )()3( 2 )3()22( 2 )2()( 2 )()(hafhafhafaf h 2 )()3( 2 )3()22(bfhafhafhf
Формула трапецийh hafaf S 2 )()( 1 h bfhaf h hafhaf h hafaf S 2 )()3( 2 )3()22( 2 )2()( 2 )()(hafhafhafaf h 2 )()3( 2 )3()22(bfhafhafhf
 Формула трапеций h fa fahfahfah fb() ()()() () 2 23 2 3 1 )( 2 )()( i ihaf bfaf h fxdxh fafb faih a b i n () () 21 1 где h ba n
Формула трапеций h fa fahfahfah fb() ()()() () 2 23 2 3 1 )( 2 )()( i ihaf bfaf h fxdxh fafb faih a b i n () () 21 1 где h ba n
 Формула трапеций Вычисление приближенного значения интеграла свелось к вычислению суммы значений подынтегральной функции. Абсолютной погрешностью называют разность точного и приближенного значений. формула для оценки погрешности в вычислении интеграла xfh ab R max
Формула трапеций Вычисление приближенного значения интеграла свелось к вычислению суммы значений подынтегральной функции. Абсолютной погрешностью называют разность точного и приближенного значений. формула для оценки погрешности в вычислении интеграла xfh ab R max
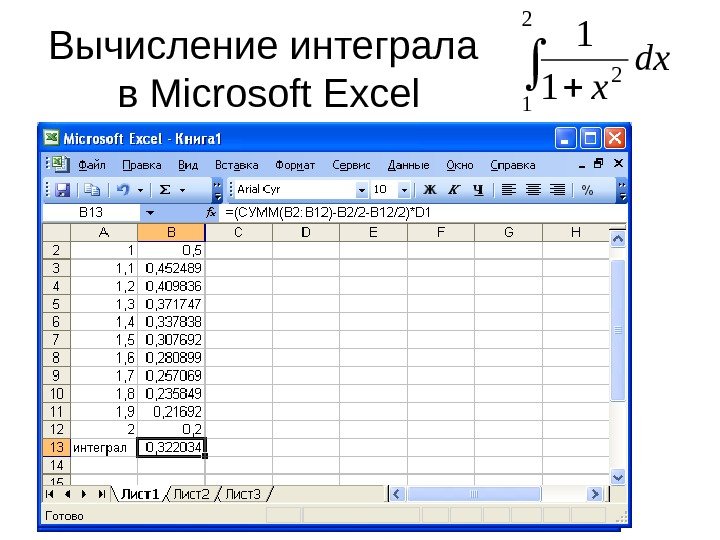
 Задание 1 вычислить приближенное значение интеграла 2 1 1 dx x с числом разбиений интервала интегрирования на 10 частей. Сравнить полученное значение интеграла с точным, определенным по формуле Ньютона-Лейбница (используя первообразную функцию).
Задание 1 вычислить приближенное значение интеграла 2 1 1 dx x с числом разбиений интервала интегрирования на 10 частей. Сравнить полученное значение интеграла с точным, определенным по формуле Ньютона-Лейбница (используя первообразную функцию).
 Вычисление интеграла в Microsoft Excel 2 1 1 dx x
Вычисление интеграла в Microsoft Excel 2 1 1 dx x

