Плоскость Геометрическое место точек координаты которых в

Плоскость

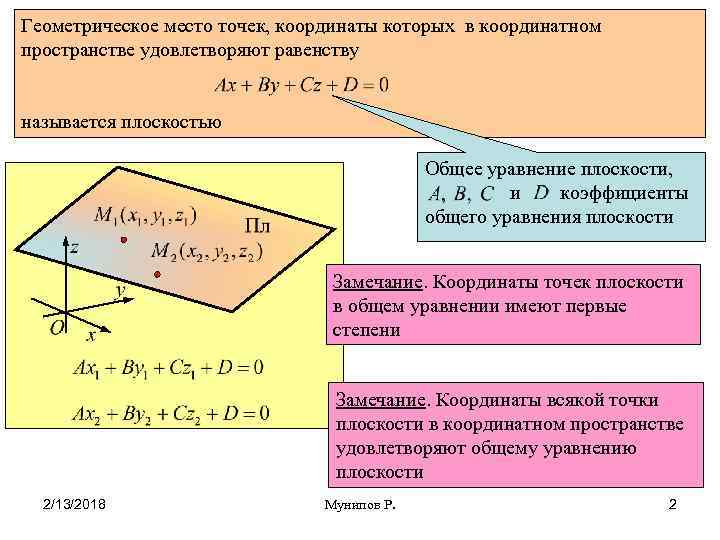Геометрическое место точек, координаты которых в координатном пространстве удовлетворяют равенству называется плоскостью Общее уравнение плоскости, и коэффициенты общего уравнения плоскости Замечание. Координаты точек плоскости в общем уравнении имеют первые степени Замечание. Координаты всякой точки плоскости в координатном пространстве удовлетворяют общему уравнению плоскости 2/13/2018 Мунипов Р. 2

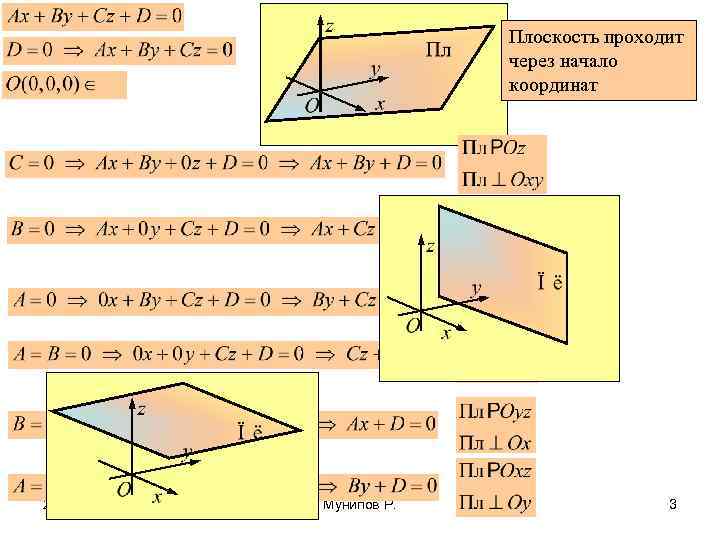Плоскость проходит через начало координат 2/13/2018 Мунипов Р. 3

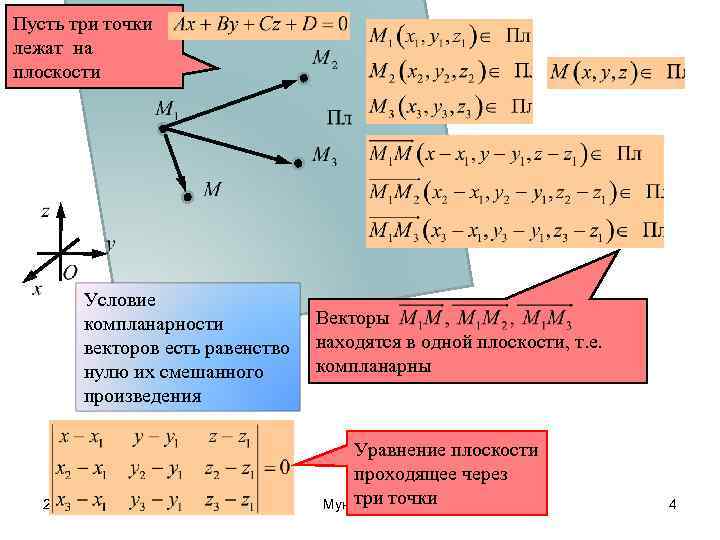Пусть три точки лежат на плоскости Условие компланарности векторов есть равенство нулю их смешанного произведения 2/13/2018 Векторы находятся в одной плоскости, т. е. компланарны Уравнение плоскости проходящее через три точки Мунипов Р. 4

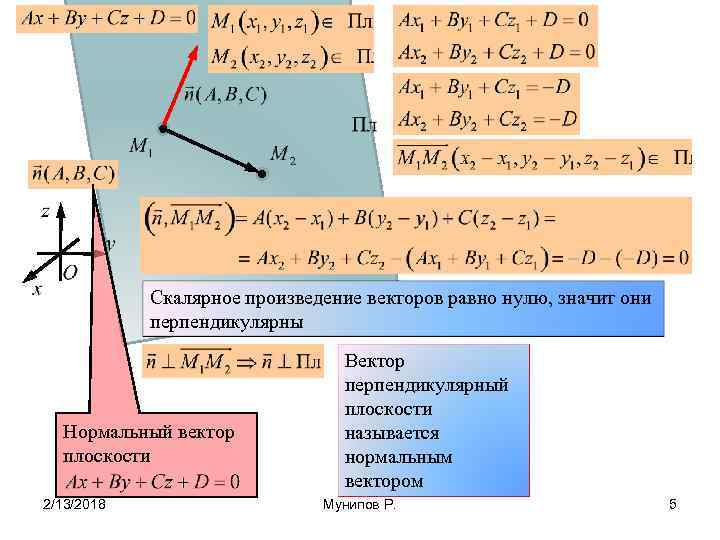Скалярное произведение векторов равно нулю, значит они перпендикулярны Нормальный вектор плоскости 2/13/2018 Вектор перпендикулярный плоскости называется нормальным вектором Мунипов Р. 5

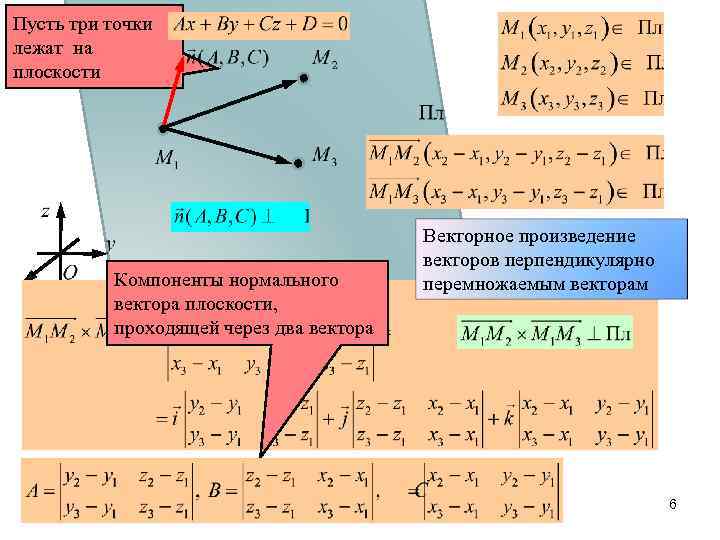Пусть три точки лежат на плоскости Компоненты нормального вектора плоскости, проходящей через два вектора 2/13/2018 Мунипов Р. Векторное произведение векторов перпендикулярно перемножаемым векторам 6

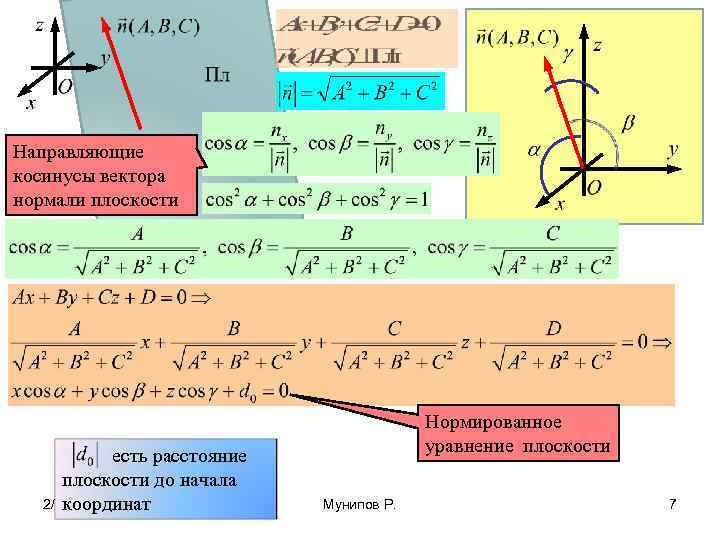Направляющие косинусы вектора нормали плоскости есть расстояние плоскости до начала 2/13/2018 координат Нормированное уравнение плоскости Мунипов Р. 7

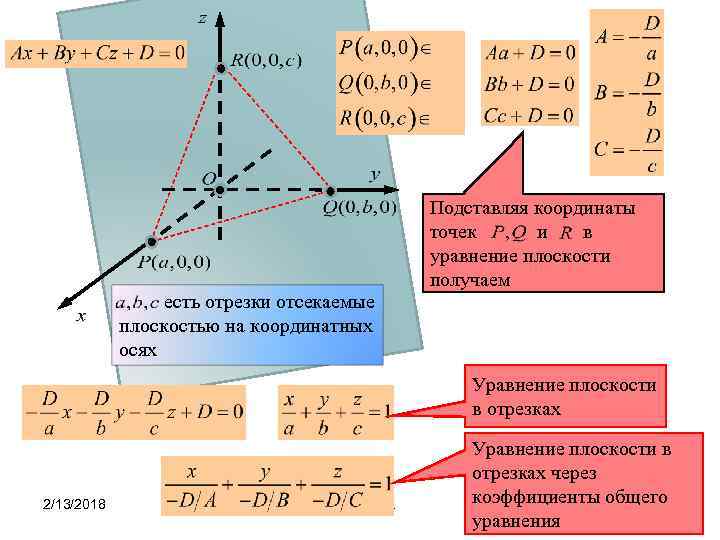есть отрезки отсекаемые плоскостью на координатных осях Подставляя координаты точек и в уравнение плоскости получаем Уравнение плоскости в отрезках 2/13/2018 Мунипов Р. Уравнение плоскости в отрезках через коэффициенты общего 8 уравнения

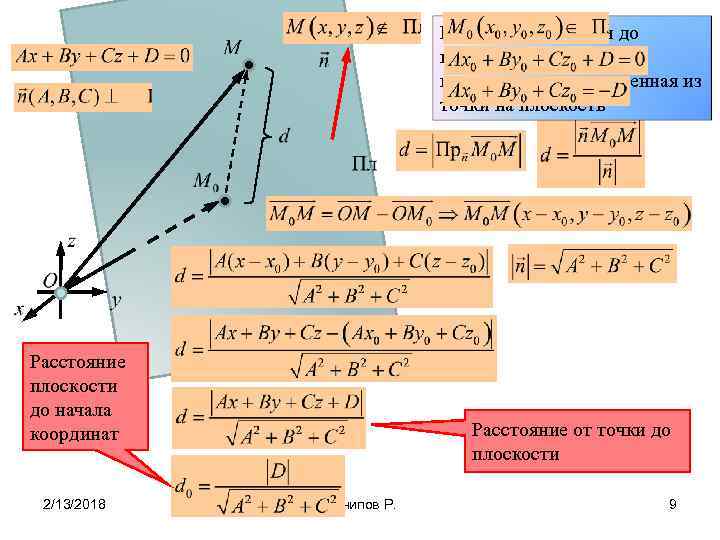Расстояние от точки до плоскости есть длина перпендикуляра опущенная из точки на плоскость Расстояние плоскости до начала координат 2/13/2018 Расстояние от точки до плоскости Мунипов Р. 9

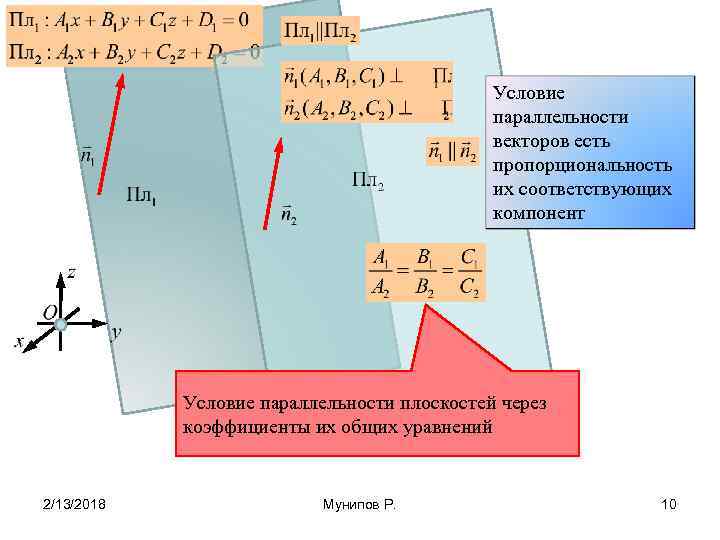Условие параллельности векторов есть пропорциональность их соответствующих компонент Условие параллельности плоскостей через коэффициенты их общих уравнений 2/13/2018 Мунипов Р. 10

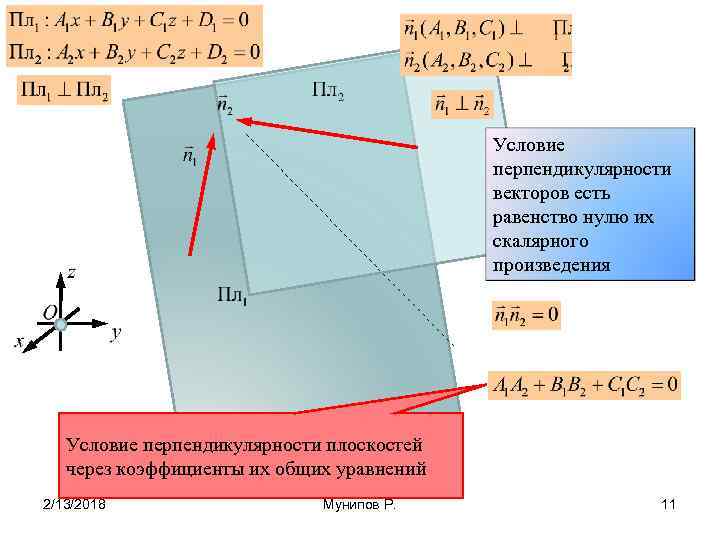Условие перпендикулярности векторов есть равенство нулю их скалярного произведения Условие перпендикулярности плоскостей через коэффициенты их общих уравнений 2/13/2018 Мунипов Р. 11

Угол между двумя непараллельными плоскостями определяется углом между перпендикулярами, которые восстановлены из точки на линии пересечения рассматриваемых плоскостей лежат в них Выражение для косинуса угла между двумя непараллельными плоскостями через коэффициенты их общих уравнений 2/13/2018 Угол между двумя непараллельными плоскостями есть угол между их нормальными векторами, косинус которого равен отношению их скалярного произведения к произведению их модулей Мунипов Р. 12

Через точку и два неколлинеарных вектора проведем плоскость Параметрическое уравнение плоскости в координатной форме Уравнение плоскости проходящее через точку и два неколлинеарных 2/13/2018 вектора Мунипов Р. Параметрическое уравнение плоскости в векторной форме Линейная зависимость векторов 13