Первообразная Интеграл Первообразная Интеграл Автор: Казадаева Надежда Ивановна

Первообразная Интеграл Автор: Казадаева Надежда Ивановна

Содержание Понятие первообразной Неопределенный интеграл Таблица первообразных Три правила нахождения первообразных Определенный интеграл Вычисление определенного интеграла Площадь криволинейной трапеции (1) Площадь криволинейной трапеции (2) Площадь криволинейной трапеции (3) Площадь криволинейной трапеции ( 4 ) Пример (1) Пример (2)

Понятие первообразной Функцию F(x) называют первообразной для функции f(x) на интервале (a; b) , если на нем производная функции F(x) равна f(x) : Операцию, обратную дифференцированию называют интегрированием. )x(f)x(

Примеры 1. f(x) = 2 x; F(x) = x 2 F (x)= (x 2 ) = 2 x = f(x) 2. f(x) = – sin x; F(x) = с os x F (x)= (cos x) = – sin x = f(x) 3. f(x) = 6 x 2 + 4; F(x) = 2 x 3 + 4 x F (x)= (2 x 3 + 4 x) = 6 x 2 + 4 = f(x) 4. f(x) = 1/cos 2 x; F(x) = tg x F (x)= (tg x) = 1/cos 2 x= f(x)

Неопределенный интеграл Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x) называют любую ее первообразную функцию. c)x(Fdx)x(f Где С – произвольная постоянная ( const).

Примеры33 44 3 xx 4 4 1 С 4 x ; С 4 x dxx. 4 xxxx e. Ce; Сedxe. 2 xsin. Cxcos; Сxcosxdxsin. 3 ACAx; CAx. Adx. 1 xcos 1 Cxtg; Cxtgdx xcos 1.

Таблица первообразных C 1 n x 1 n х C 3 xx 2 f(x) xсos 1 2 xsin 1 2 C x 1 aln a x alnx 1 2 x 1 1 n x. Ca x xln x e. Ce x CCxxsin xcos Cxsin Ctgx Cctgx Cxloga Cxarcsin f(x) F(x)

Три правила нахождения первообразных 1 º Если F ( x ) есть первообразная для f(x) , а G(x) – первообразная для g(x) , то F(x) + G(x) есть первообразная для f(x) + g(x). 2º Если F(x) есть первообразная для f(x) , а k – постоянная, то функция k. F(x) есть первообразная для kf (х). 3º Если F(x) есть первообразная для f(x) , а k и b – постоянные, причем k ≠ 0 , то функция F(kx + b ) есть первообразная для f(kx + b). 1 k

Физический смысл первообразной

Определенный интегралa. Fb. Fx. Fdxxf b a – формула Ньютона-Лейбница. Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, образованной линиями: сверху ограниченной кривой у = f(x) , и прямыми у = 0 ; х = а ; х = b.

Вычисление определенного интеграла 516111222 2323 10 33 662 6 xx dxx 2 1232 1 2123 xxxdxxx

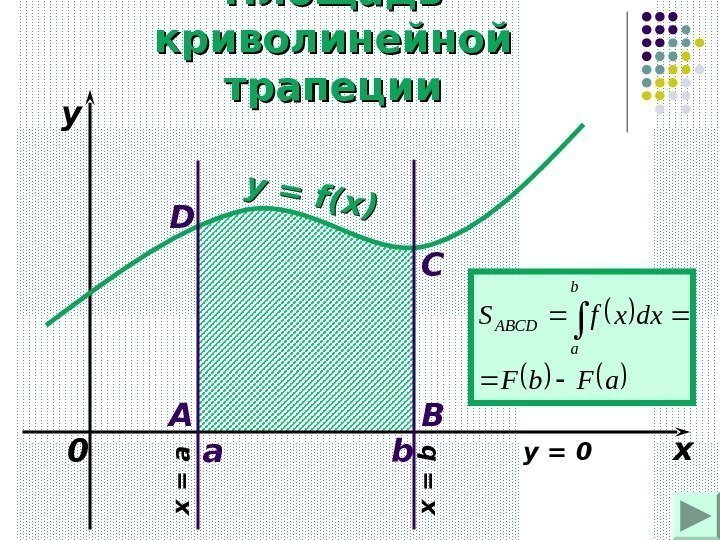
Площадь криволинейной трапеции a b xyy = f(x) 0 a. Fb. F dxxf. S b a ABCD A BCD x = a x = b y =

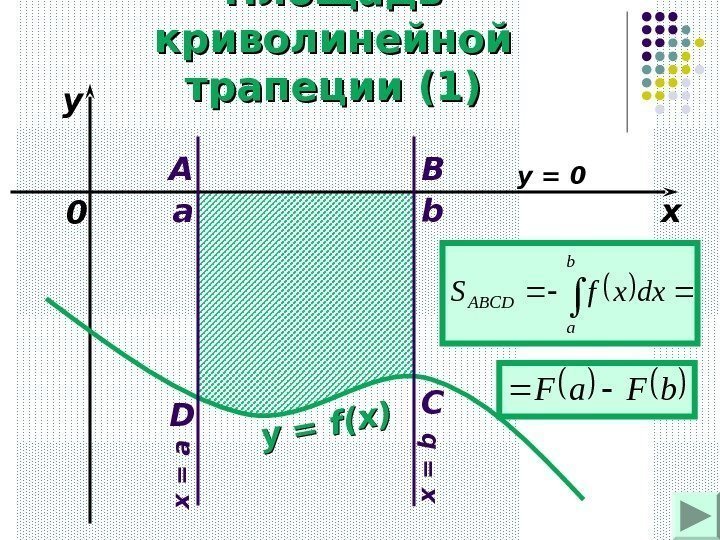
Площадь криволинейной трапеции (1) a b xyy = f(x) 0 A B C D x = a x = b y = 0 b a. ABCD dxxf. S b. Fa.

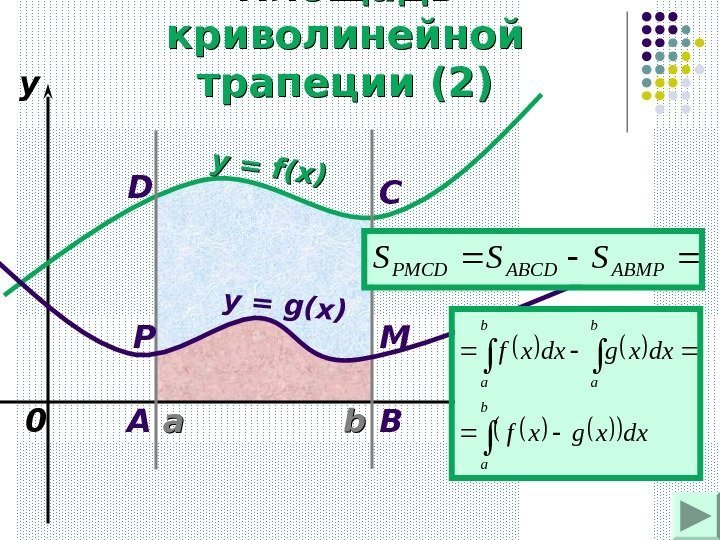
aa bb xyy = f(x) 0 y = g(x) A BCD MP ABMPABCDPMCDSSS b ab a dxxgxf dxxgdxxf. Площадь криволинейной трапеции (2)

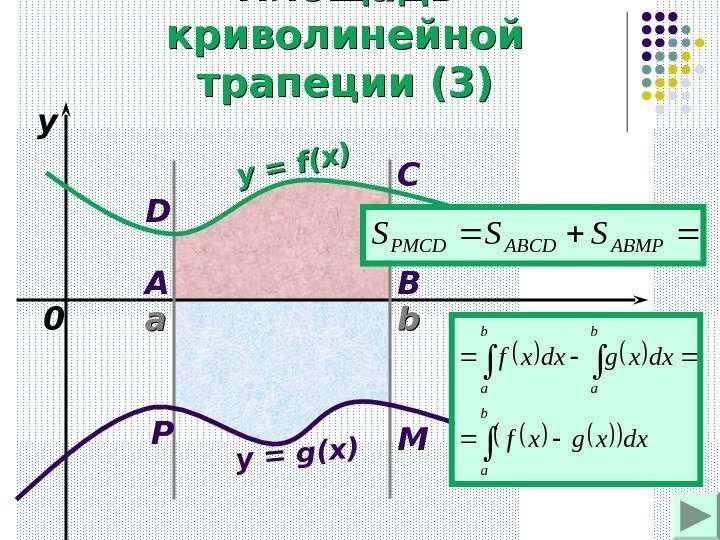
aa bb xyy = f(x) 0 y = g(x) A BC D MP b ab a dxxgxf dxxgdxxf ABMPABCDPMCD SSSПлощадь криволинейной трапеции (3)

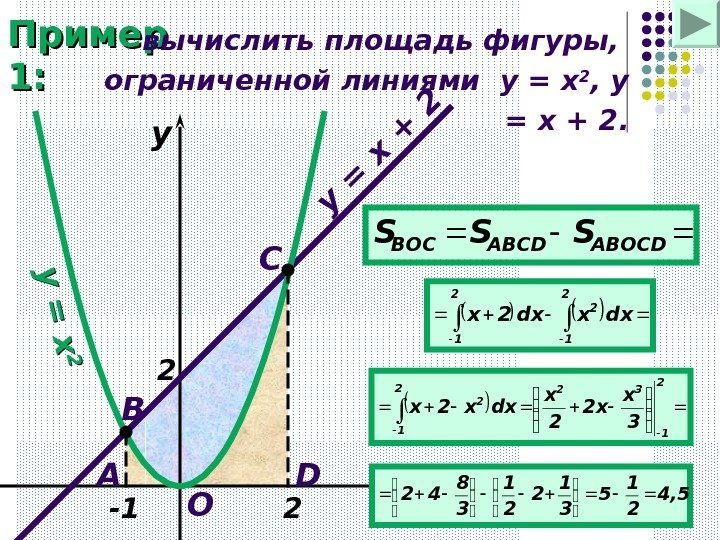
Пример 1: вычислить площадь фигуры, ограниченной линиями y = x 2 , y = x + 2. xyy = x 2 y = x + 2 -1 2 A B O DC 2 ABOCDABCDВОСSSS 2 1 2 dxxdx 2 x 4, 5 2 1 5 3 1 2 2 1 3 8 42 2 1 322 1 2 3 x 2 x 2 x dxх2 х

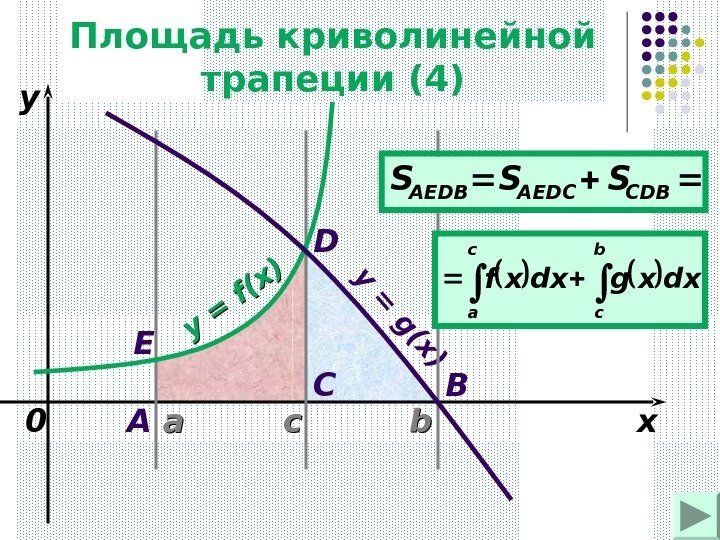
aa bb xyy = f(x ) 0 y = g (x ) A BCD сс. Е СDBAEDCАЕDВSSS с a b с dxxgdxxf. Площадь криволинейной трапеции ( 4 )

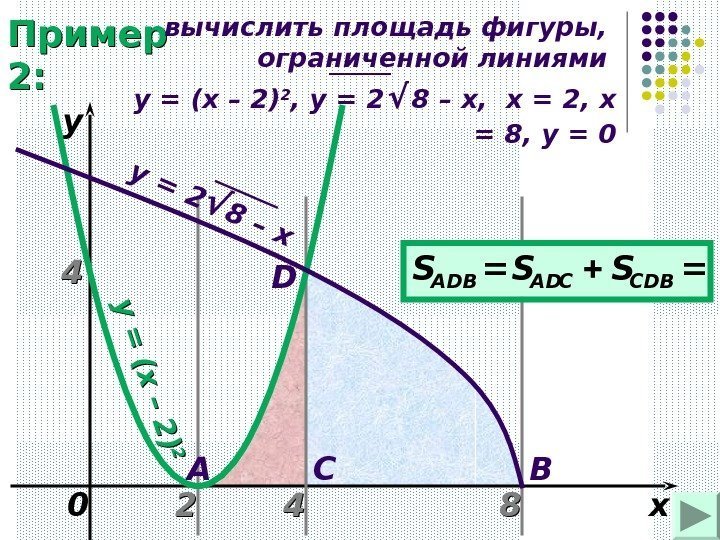
Пример 2: 22 88 xy = ( x – 2 )20 A BCD 44 y y = 2√ 8 – x 44 вычислить площадь фигуры, ограниченной линиями y = ( x – 2) 2 , y = 2 √ 8 – x , х = 2, х = 8, у = 0 СDBADСАDВSSS

8 4 4 2 34 2 8 4 2 3 x 8 x 84 3 2 x dxх-82 dx 2 -x 3 48484 3 88884 3 22 3 24 33 Пример 2: вычислить площадь фигуры, ограниченной линиями y = ( x – 2) 2 , y = 2 √ 8 – x , х = 2, х = 8, у =