Перпендикулярность в пространстве. Урок № 19 baa




19_g_10_kl._perpendikulyarnosty.pptx
- Размер: 513.6 Кб
- Автор:
- Количество слайдов: 16
Описание презентации Перпендикулярность в пространстве. Урок № 19 baa по слайдам
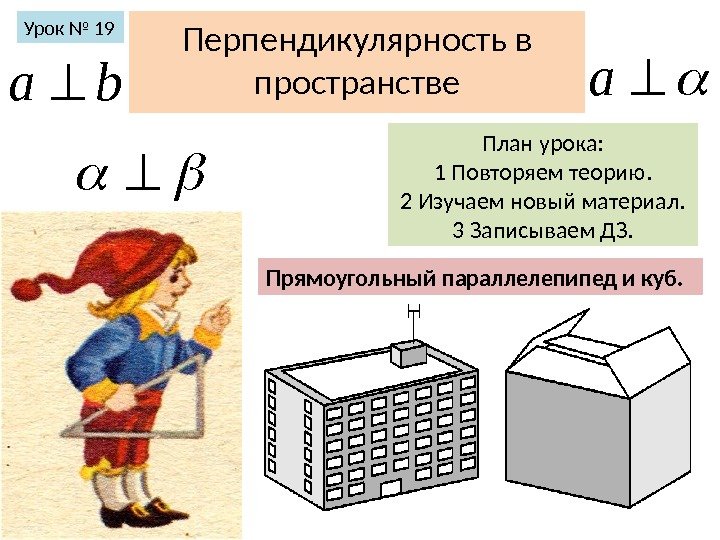
 Перпендикулярность в пространстве. Урок № 19 baa План урока: 1 Повторяем теорию. 2 Изучаем новый материал. 3 Записываем ДЗ. Прямоугольный параллелепипед и куб.
Перпендикулярность в пространстве. Урок № 19 baa План урока: 1 Повторяем теорию. 2 Изучаем новый материал. 3 Записываем ДЗ. Прямоугольный параллелепипед и куб.
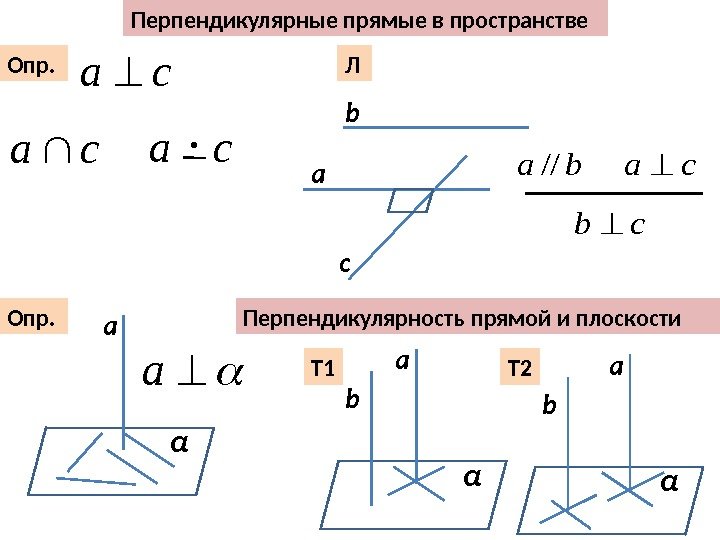
 Перпендикулярность прямой и плоскостиa. Опр. a α Т 1 a αb Т 2 a αb. Перпендикулярные прямые в пространстве Опр. сa сa ·ca Л a b c сaba// cb
Перпендикулярность прямой и плоскостиa. Опр. a α Т 1 a αb Т 2 a αb. Перпендикулярные прямые в пространстве Опр. сa сa ·ca Л a b c сaba// cb
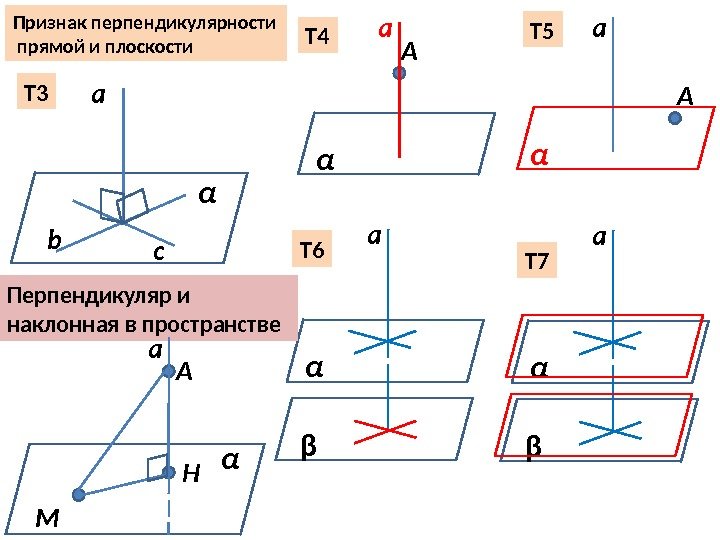
 Т 4 Т 5 a А αА α a βТ 6 α a βТ 7 Признак перпендикулярности прямой и плоскости a α b с. Т 3 Перпендикуляр и наклонная в пространстве a αА Н М
Т 4 Т 5 a А αА α a βТ 6 α a βТ 7 Признак перпендикулярности прямой и плоскости a α b с. Т 3 Перпендикуляр и наклонная в пространстве a αА Н М
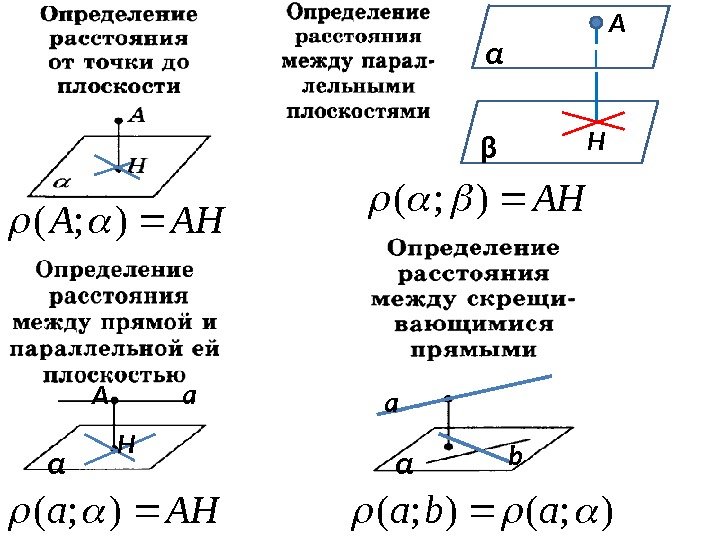
 АНА); (α A β H АН); ( a α A H АНа); ( a b α); (abа
АНА); (α A β H АН); ( a α A H АНа); ( a b α); (abа
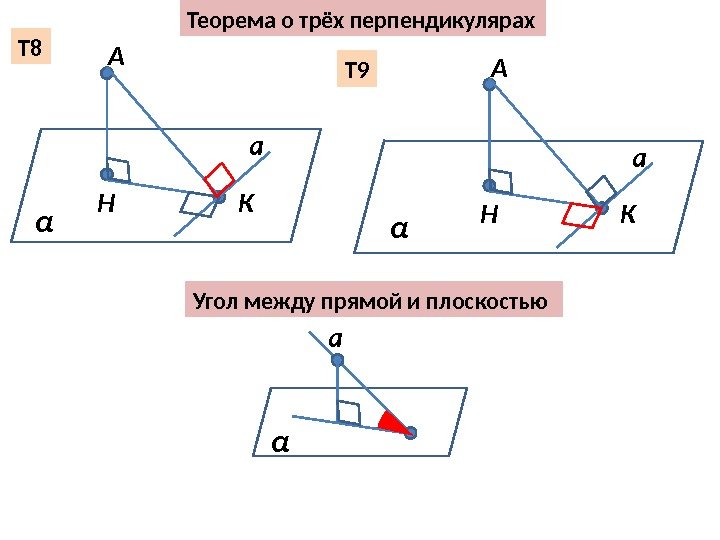
 Теорема о трёх перпендикулярах А Н К α a. Т 8 Т 9 А Н К α a Угол между прямой и плоскостью a α
Теорема о трёх перпендикулярах А Н К α a. Т 8 Т 9 А Н К α a Угол между прямой и плоскостью a α
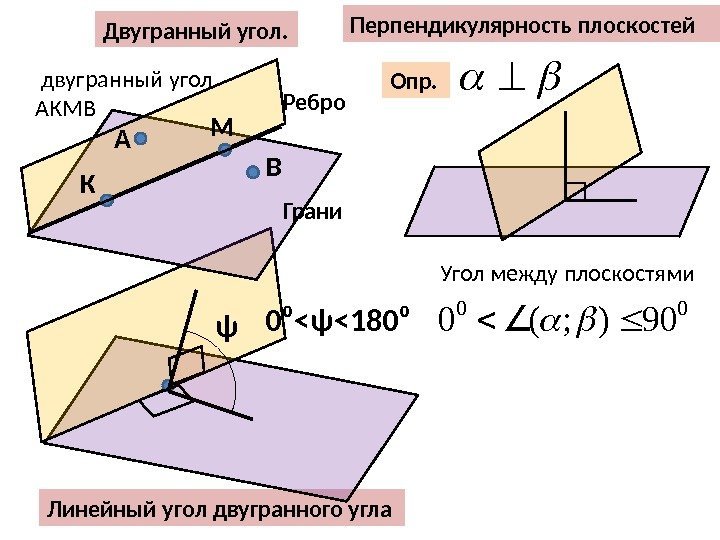
 Линейный угол двугранного угла ψ 0⁰<ψ<180⁰Двугранный угол. Ребро Грани А К М В двугранный угол АКМВ Перпендикулярность плоскостей Опр. 00 90); (0 Угол между плоскостями
Линейный угол двугранного угла ψ 0⁰<ψ<180⁰Двугранный угол. Ребро Грани А К М В двугранный угол АКМВ Перпендикулярность плоскостей Опр. 00 90); (0 Угол между плоскостями
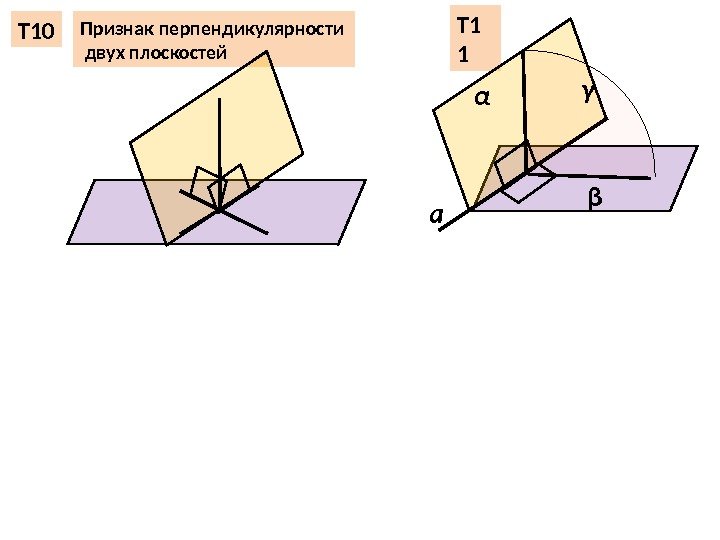
 Признак перпендикулярности двух плоскостей. Т 10 Т 1 1 α βγ а
Признак перпендикулярности двух плоскостей. Т 10 Т 1 1 α βγ а
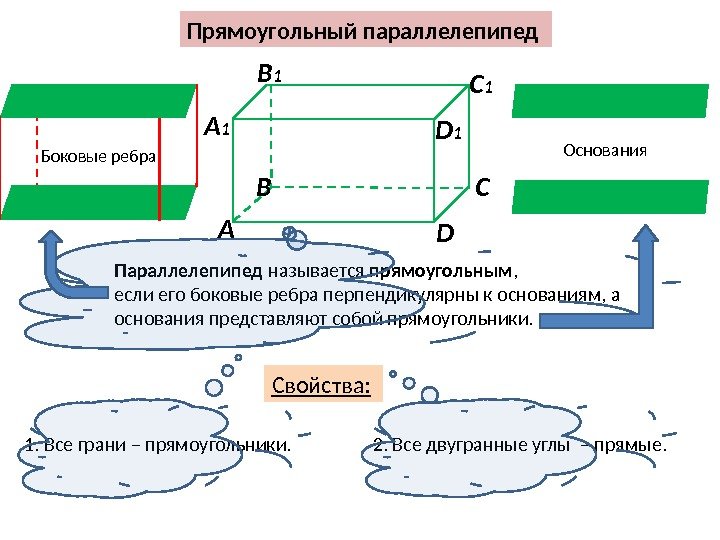
 Прямоугольный параллелепипед А В С DА 1 B 1 C 1 D 1 Свойства: Параллелепипед называется прямоугольным , если его боковые ребра перпендикулярны к основаниям, а основания представляют собой прямоугольники. 1. Все грани – прямоугольники. 2. Все двугранные углы – прямые. Боковые ребра Основания
Прямоугольный параллелепипед А В С DА 1 B 1 C 1 D 1 Свойства: Параллелепипед называется прямоугольным , если его боковые ребра перпендикулярны к основаниям, а основания представляют собой прямоугольники. 1. Все грани – прямоугольники. 2. Все двугранные углы – прямые. Боковые ребра Основания
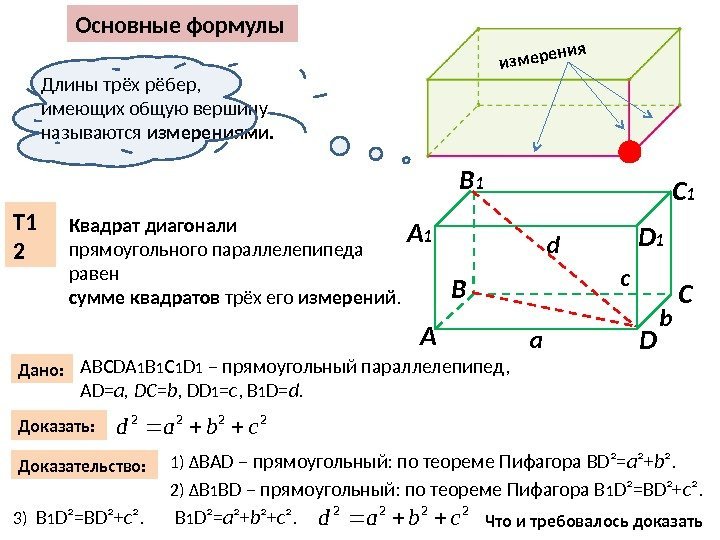
 2222 cbаd. Длины трёх рёбер, имеющих общую вершину называются измерениями. Основные формулы Т 1 2 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. А В С DА 1 B 1 C 1 D 1 a bc Дано: Доказать: Доказательство: d ABCDA 1 B 1 C 1 D 1 – прямоугольный параллелепипед, AD= a, DC=b , DD 1 = c , B 1 D= d. 1) Δ BAD – прямоугольный: по теореме Пифагора BD²= a ²+ b ². 2) Δ B 1 BD – прямоугольный: по теореме Пифагора B 1 D²=BD²+ c ². 3) B 1 D²=BD²+ c ². 2222 cbаd B 1 D²= a ²+ b ²+ c ². Что и требовалось доказать измерения
2222 cbаd. Длины трёх рёбер, имеющих общую вершину называются измерениями. Основные формулы Т 1 2 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. А В С DА 1 B 1 C 1 D 1 a bc Дано: Доказать: Доказательство: d ABCDA 1 B 1 C 1 D 1 – прямоугольный параллелепипед, AD= a, DC=b , DD 1 = c , B 1 D= d. 1) Δ BAD – прямоугольный: по теореме Пифагора BD²= a ²+ b ². 2) Δ B 1 BD – прямоугольный: по теореме Пифагора B 1 D²=BD²+ c ². 3) B 1 D²=BD²+ c ². 2222 cbаd B 1 D²= a ²+ b ²+ c ². Что и требовалось доказать измерения
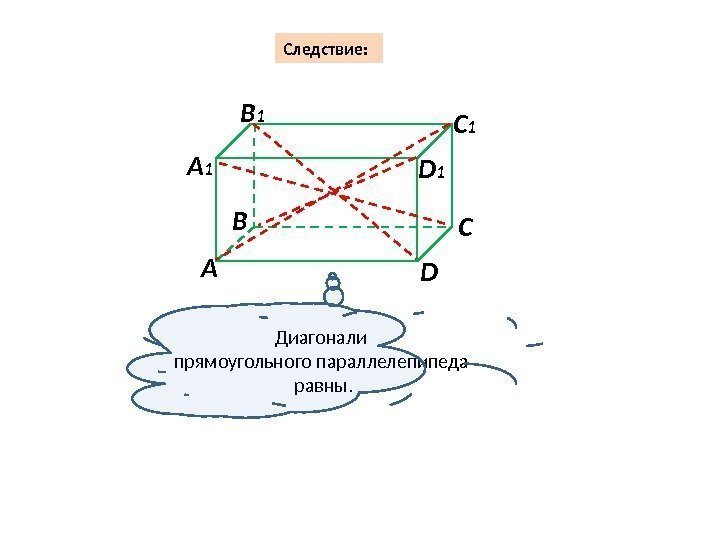
 А В С DА 1 B 1 C 1 D 1 Следствие: Диагонали прямоугольного параллелепипеда равны.
А В С DА 1 B 1 C 1 D 1 Следствие: Диагонали прямоугольного параллелепипеда равны.
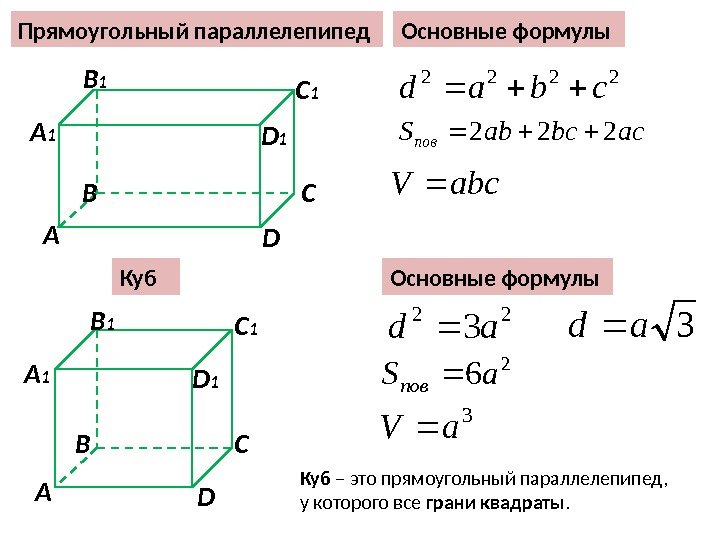
 А В С DА 1 B 1 C 1 D 1 Прямоугольный параллелепипед Основные формулы 2222 cbаd acbcаb. Sпов 222 аbc. V Куб А В С DА 1 B 1 C 1 D 1 Основные формулы 22 3 аd 2 6 а. Sпов 3 а. V Куб – это прямоугольный параллелепипед, у которого все грани квадраты.
А В С DА 1 B 1 C 1 D 1 Прямоугольный параллелепипед Основные формулы 2222 cbаd acbcаb. Sпов 222 аbc. V Куб А В С DА 1 B 1 C 1 D 1 Основные формулы 22 3 аd 2 6 а. Sпов 3 а. V Куб – это прямоугольный параллелепипед, у которого все грани квадраты.
 Задача 1 Задача 2 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда. № 27100 ЕГЭ Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины. № 27079 ЕГЭ Задача 3 Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол 45 ⁰. Найдите объем параллелепипеда. № 27103 ЕГЭ Решите задачи:
Задача 1 Задача 2 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда. № 27100 ЕГЭ Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины. № 27079 ЕГЭ Задача 3 Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол 45 ⁰. Найдите объем параллелепипеда. № 27103 ЕГЭ Решите задачи:
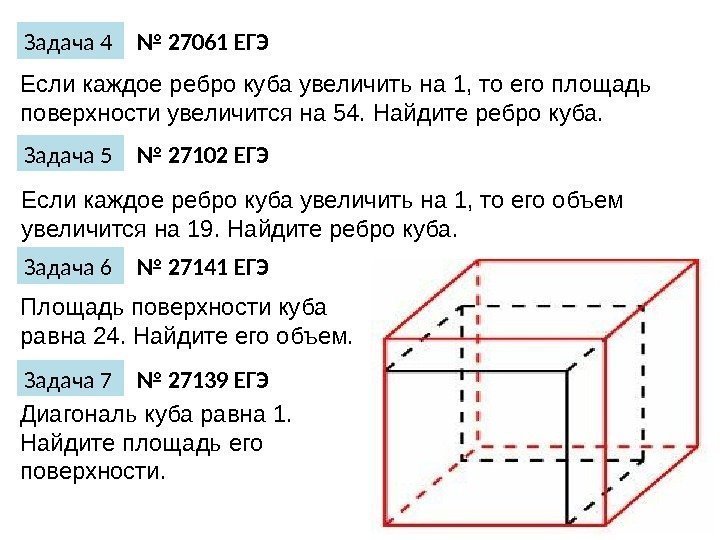
 Задача 4 Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. № 27061 ЕГЭ № 27102 ЕГЭЗадача 5 Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба. № 27141 ЕГЭЗадача 6 Площадь поверхности куба равна 24. Найдите его объем. Диагональ куба равна 1. Найдите площадь его поверхности. Задача 7 № 27139 ЕГЭ
Задача 4 Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. № 27061 ЕГЭ № 27102 ЕГЭЗадача 5 Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба. № 27141 ЕГЭЗадача 6 Площадь поверхности куба равна 24. Найдите его объем. Диагональ куба равна 1. Найдите площадь его поверхности. Задача 7 № 27139 ЕГЭ
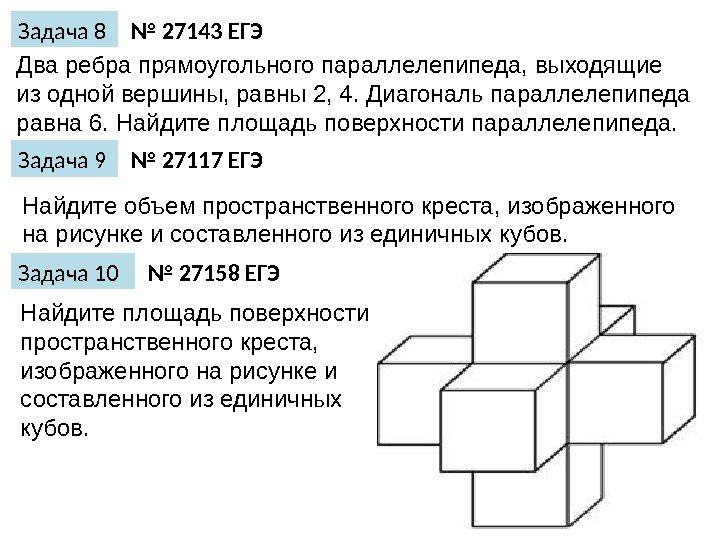
 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда. Задача 8 № 27143 ЕГЭ Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов. Задача 9 № 27117 ЕГЭ Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов. Задача 10 № 27158 ЕГЭ
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда. Задача 8 № 27143 ЕГЭ Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов. Задача 9 № 27117 ЕГЭ Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов. Задача 10 № 27158 ЕГЭ
 Домашнее задание № 19 Знать формулировки изученной теории п. 15 — 24 учебника Решите задачи Задача 1 Задача 2 № 27055 ЕГЭ Площадь поверхности куба равна 18. Найдите его диагональ. № 27056 ЕГЭ Объем куба равен 8. Найдите площадь его поверхности. Задача 3 № 27098 ЕГЭ Диагональ куба равна . Найдите его объем. Задача 4 № 27099 ЕГЭ Объем куба равен . Найдите его диагональ. № 27081 ЕГЭЗадача 5 Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
Домашнее задание № 19 Знать формулировки изученной теории п. 15 — 24 учебника Решите задачи Задача 1 Задача 2 № 27055 ЕГЭ Площадь поверхности куба равна 18. Найдите его диагональ. № 27056 ЕГЭ Объем куба равен 8. Найдите площадь его поверхности. Задача 3 № 27098 ЕГЭ Диагональ куба равна . Найдите его объем. Задача 4 № 27099 ЕГЭ Объем куба равен . Найдите его диагональ. № 27081 ЕГЭЗадача 5 Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
 № 27128 ЕГЭЗадача 6 Рёбра прямоугольного параллелепипеда равны 1, 2, 3. Найдите площадь его поверхности. Задача 7 Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза? № 27130 ЕГЭ
№ 27128 ЕГЭЗадача 6 Рёбра прямоугольного параллелепипеда равны 1, 2, 3. Найдите площадь его поверхности. Задача 7 Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза? № 27130 ЕГЭ

