Перпендикулярность в пространстве. Урок № 18 baa

18_g_10_kl._perpendikulyarnosty.pptx
- Размер: 683.8 Кб
- Автор: Алина Али
- Количество слайдов: 15
Описание презентации Перпендикулярность в пространстве. Урок № 18 baa по слайдам
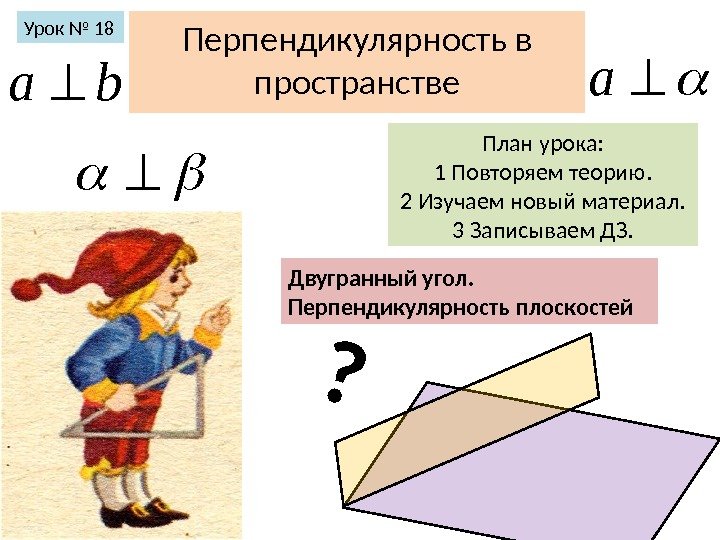
 Перпендикулярность в пространстве. Урок № 18 baa План урока: 1 Повторяем теорию. 2 Изучаем новый материал. 3 Записываем ДЗ. Двугранный угол. Перпендикулярность плоскостей ¿
Перпендикулярность в пространстве. Урок № 18 baa План урока: 1 Повторяем теорию. 2 Изучаем новый материал. 3 Записываем ДЗ. Двугранный угол. Перпендикулярность плоскостей ¿
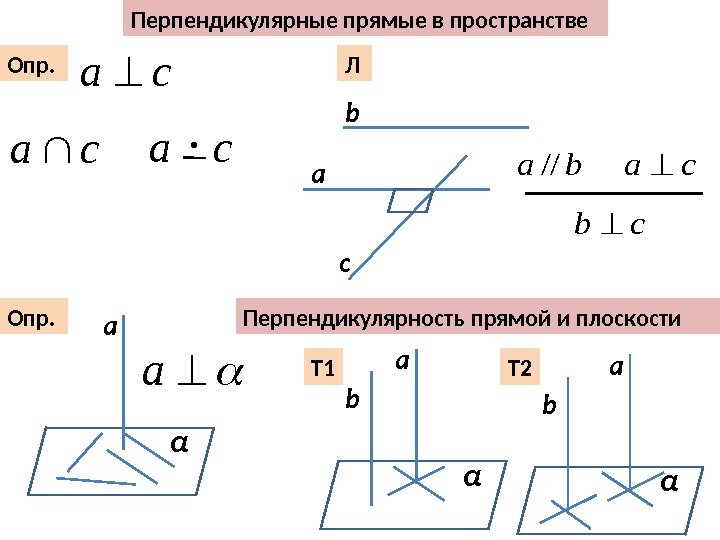
 Перпендикулярность прямой и плоскостиa. Опр. a α Т 1 a αb Т 2 a αb. Перпендикулярные прямые в пространстве Опр. сa сa ·ca Л a b c сaba// cb
Перпендикулярность прямой и плоскостиa. Опр. a α Т 1 a αb Т 2 a αb. Перпендикулярные прямые в пространстве Опр. сa сa ·ca Л a b c сaba// cb
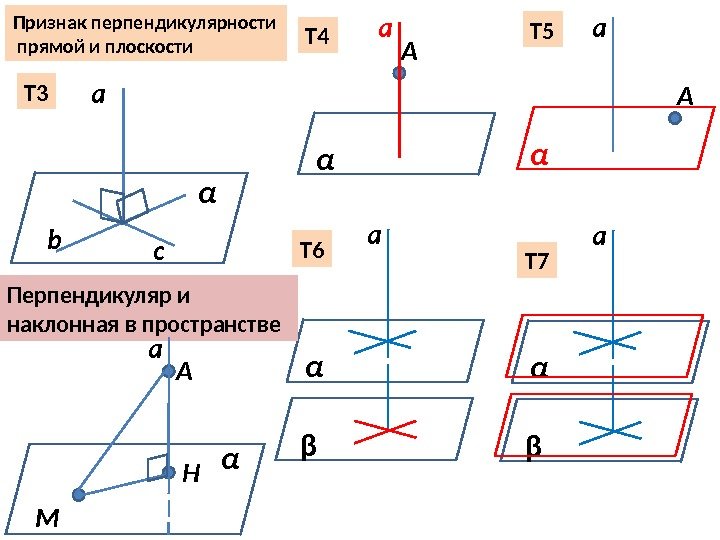
 Т 4 Т 5 a А αА α a βТ 6 α a βТ 7 Признак перпендикулярности прямой и плоскости a α b с. Т 3 Перпендикуляр и наклонная в пространстве a αА Н М
Т 4 Т 5 a А αА α a βТ 6 α a βТ 7 Признак перпендикулярности прямой и плоскости a α b с. Т 3 Перпендикуляр и наклонная в пространстве a αА Н М
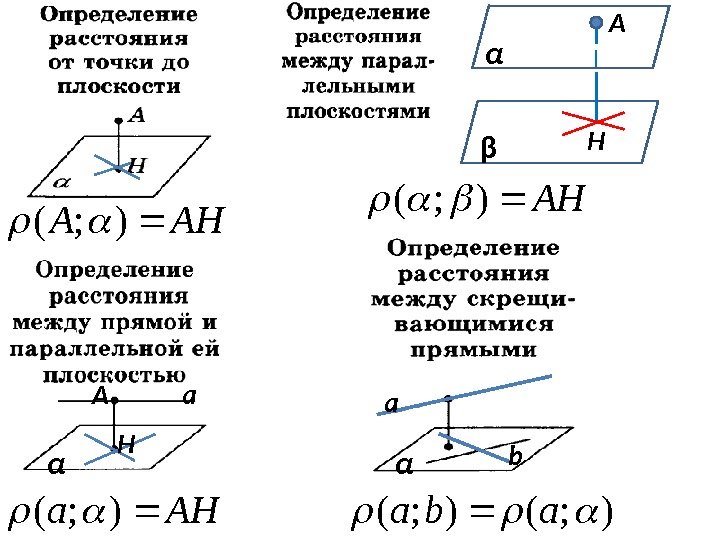
 АНА); (α A β H АН); ( a α A H АНа); ( a b α); (abа
АНА); (α A β H АН); ( a α A H АНа); ( a b α); (abа
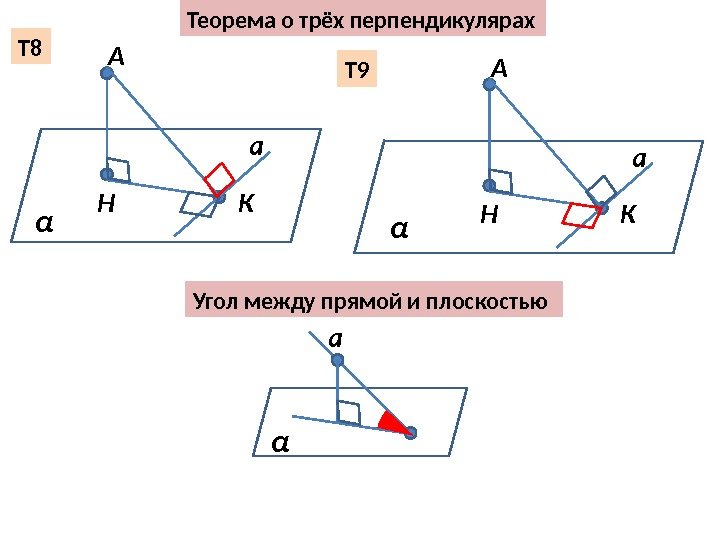
 Теорема о трёх перпендикулярах А Н К α a. Т 8 Т 9 А Н К α a Угол между прямой и плоскостью a α
Теорема о трёх перпендикулярах А Н К α a. Т 8 Т 9 А Н К α a Угол между прямой и плоскостью a α
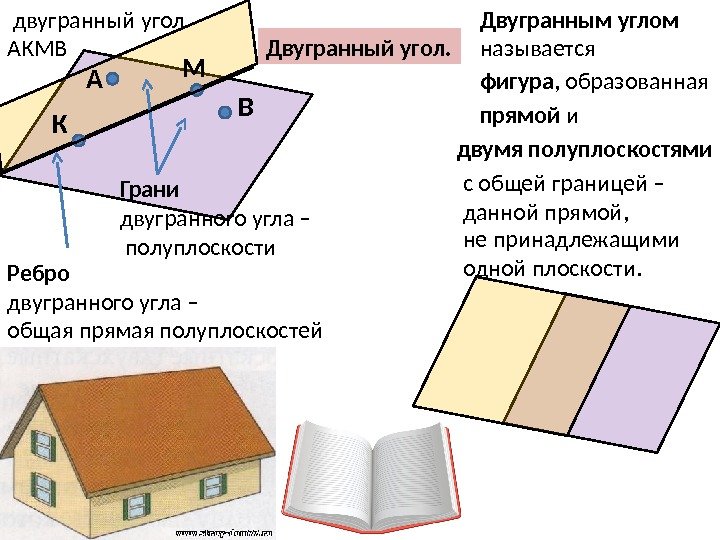
 Двугранный угол. Двугранным углом называется Ребро двугранного угла – общая прямая полуплоскостей Грани двугранного угла – полуплоскости. А К М В двугранный угол АКМВ фигура , образованная прямой и двумя полуплоскостями с общей границей – данной прямой, не принадлежащими одной плоскости.
Двугранный угол. Двугранным углом называется Ребро двугранного угла – общая прямая полуплоскостей Грани двугранного угла – полуплоскости. А К М В двугранный угол АКМВ фигура , образованная прямой и двумя полуплоскостями с общей границей – данной прямой, не принадлежащими одной плоскости.
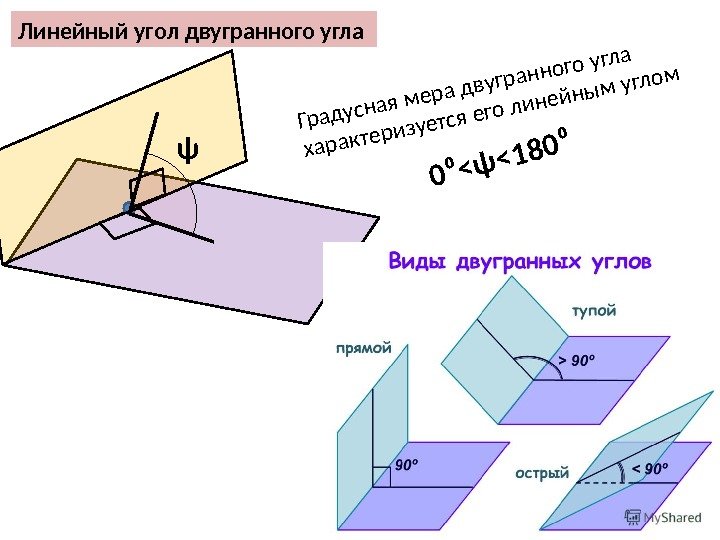
 Линейный угол двугранного угла Градусная мера двугранного угла характеризуется его линейным углом ψ 0⁰<ψ<180⁰
Линейный угол двугранного угла Градусная мера двугранного угла характеризуется его линейным углом ψ 0⁰<ψ<180⁰
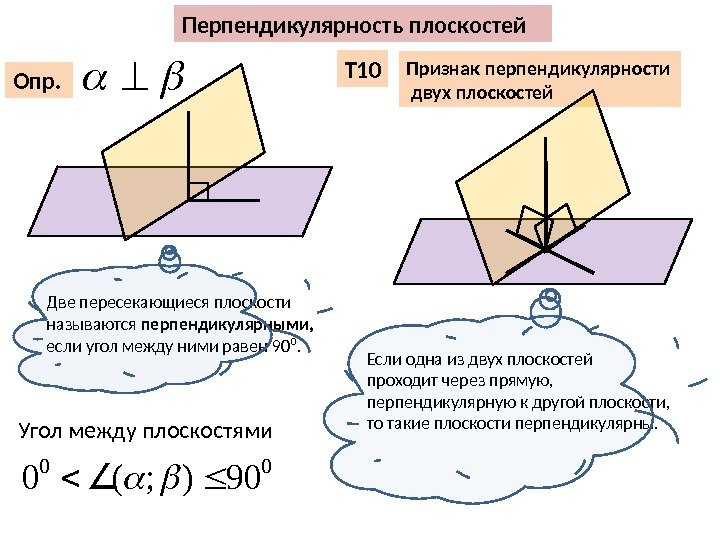
 Перпендикулярность плоскостей Опр. 00 90); (0 Угол между плоскостями Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. Признак перпендикулярности двух плоскостей. Т 10 Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90⁰.
Перпендикулярность плоскостей Опр. 00 90); (0 Угол между плоскостями Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. Признак перпендикулярности двух плоскостей. Т 10 Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90⁰.
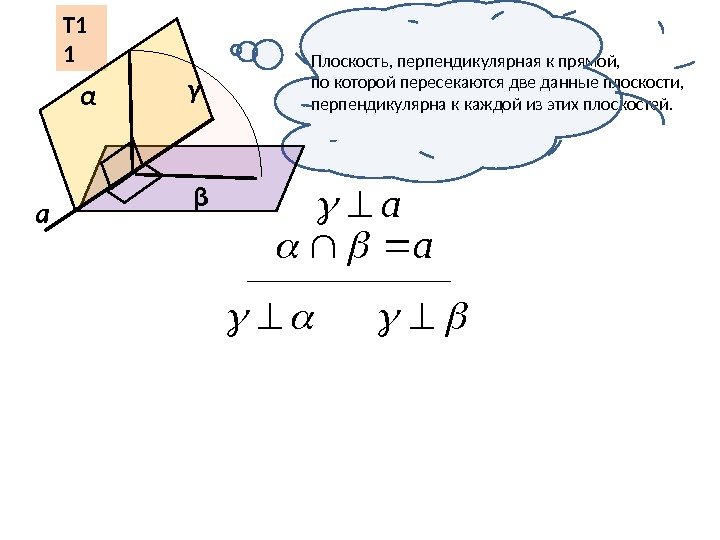
 Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей. Т 1 1 α βγ аа а
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей. Т 1 1 α βγ аа а
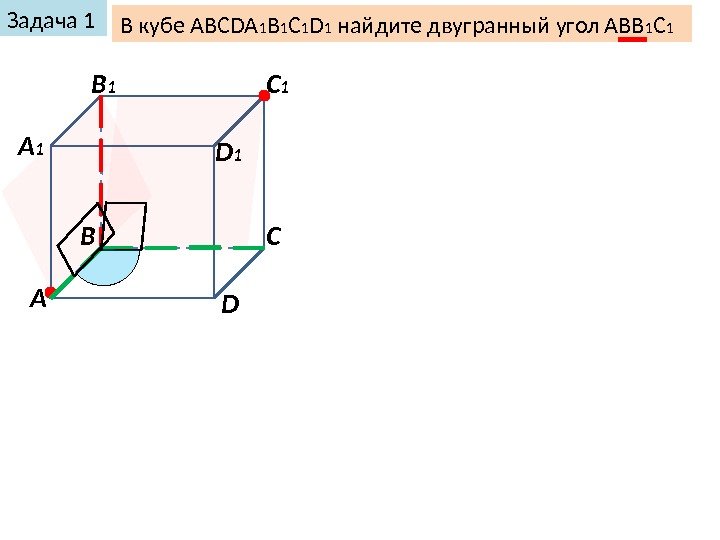
 А В С DА 1 B 1 C 1 D 1 Задача 1 В кубе ABCDA 1 B 1 C 1 D 1 найдите двугранный угол АВВ 1 С
А В С DА 1 B 1 C 1 D 1 Задача 1 В кубе ABCDA 1 B 1 C 1 D 1 найдите двугранный угол АВВ 1 С
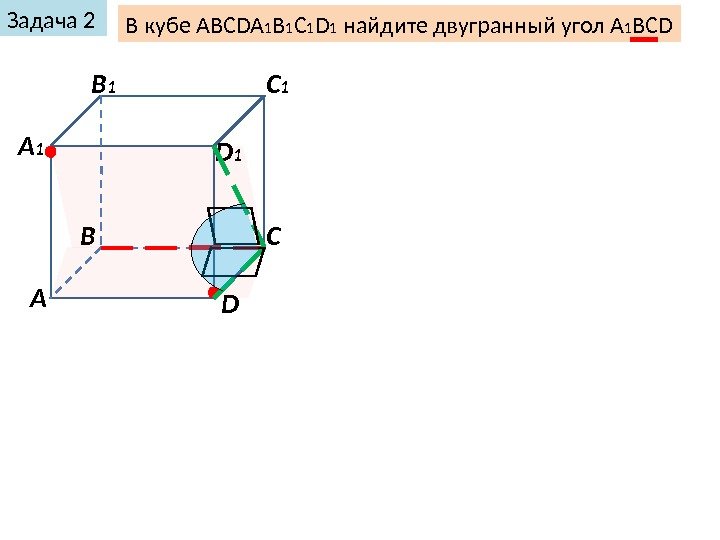
 Задача 2 В кубе ABCDA 1 B 1 C 1 D 1 найдите двугранный угол А 1 ВСD А В С DА
Задача 2 В кубе ABCDA 1 B 1 C 1 D 1 найдите двугранный угол А 1 ВСD А В С DА
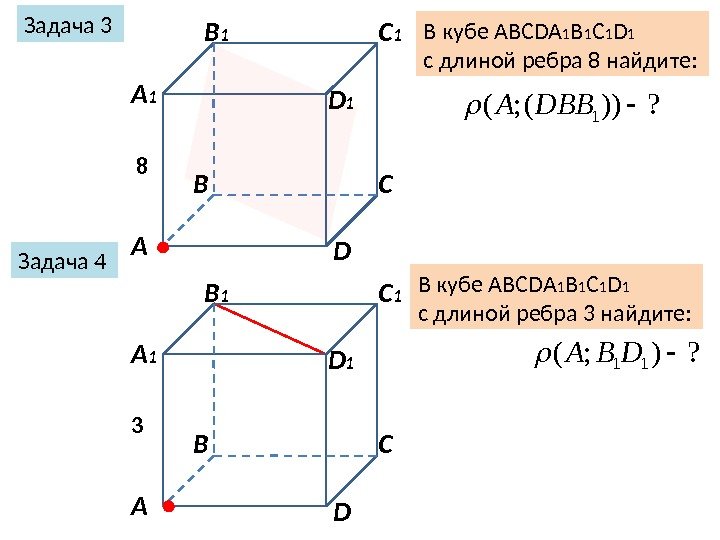
 Задача 3 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 8 найдите: А В С DА 1 B 1 C 1 D 1? ); (11 DВА Задача 4 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 3 найдите: 8 3 А В С DА 1 B 1 C 1 D 1 ? ))(; (1 DВВА
Задача 3 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 8 найдите: А В С DА 1 B 1 C 1 D 1? ); (11 DВА Задача 4 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 3 найдите: 8 3 А В С DА 1 B 1 C 1 D 1 ? ))(; (1 DВВА
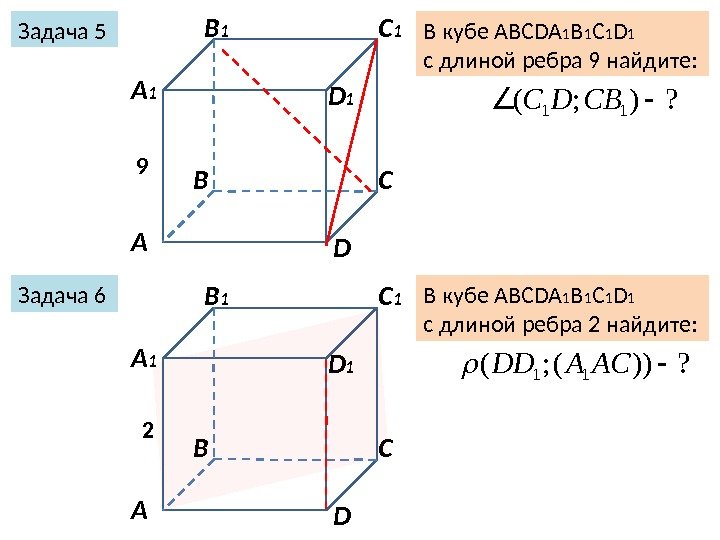
 Задача 5 А В С DА 1 B 1 C 1 D 1 Задача 6 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 9 найдите: 9? ))(; (11 AСАDD В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 2 найдите: ? ); (11 СВDС
Задача 5 А В С DА 1 B 1 C 1 D 1 Задача 6 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 9 найдите: 9? ))(; (11 AСАDD В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 2 найдите: ? ); (11 СВDС
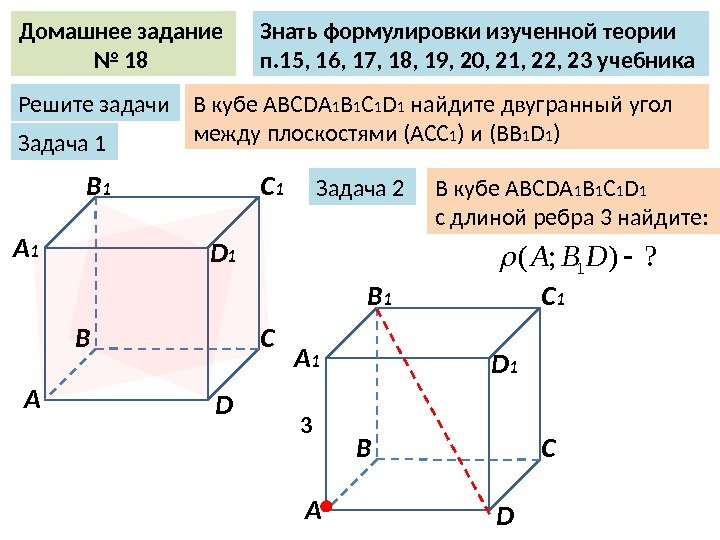
 Домашнее задание № 18 Знать формулировки изученной теории п. 15, 16, 17, 18, 19, 20, 21, 22, 23 учебника Решите задачи В кубе ABCDA 1 B 1 C 1 D 1 найдите двугранный угол между плоскостями (АСС 1 ) и (ВВ 1 D 1 ) А В С DА 1 B 1 C 1 D 1 Задача 1 Задача 2 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 3 найдите: ? ); (1 DBА А В С DА
Домашнее задание № 18 Знать формулировки изученной теории п. 15, 16, 17, 18, 19, 20, 21, 22, 23 учебника Решите задачи В кубе ABCDA 1 B 1 C 1 D 1 найдите двугранный угол между плоскостями (АСС 1 ) и (ВВ 1 D 1 ) А В С DА 1 B 1 C 1 D 1 Задача 1 Задача 2 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 3 найдите: ? ); (1 DBА А В С DА
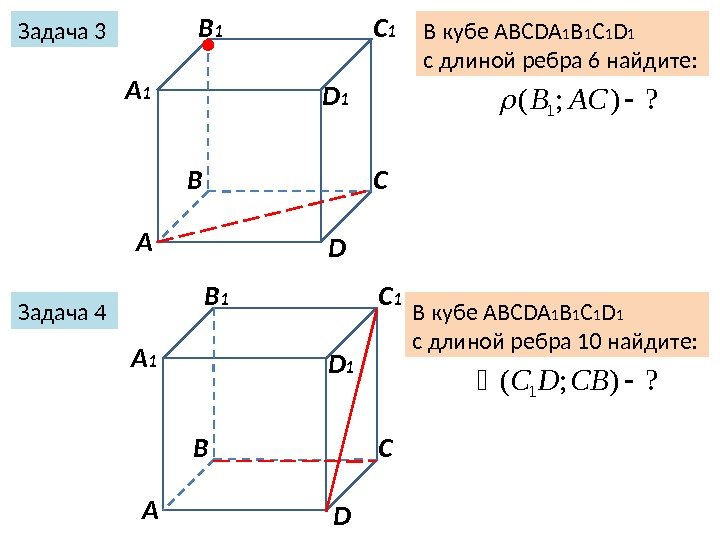
 Задача 3 Задача 4 А В С DА 1 B 1 C 1 D 1 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 6 найдите: В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 10 найдите: ? ); (1 АCB ? ); (1 CВDС
Задача 3 Задача 4 А В С DА 1 B 1 C 1 D 1 В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 6 найдите: В кубе ABCDA 1 B 1 C 1 D 1 с длиной ребра 10 найдите: ? ); (1 АCB ? ); (1 CВDС

