4976d7a18b0ad000e265ea91891a8f58.ppt
- Количество слайдов: 64
 Parsing
Parsing
 Parsing Calculate grammatical structure of program, like diagramming sentences, where: Tokens = “words” Programs = “sentences” For further information, read: Aho, Sethi, Ullman, “Compilers: Principles, Techniques, and Tools” (a. k. a, the “Dragon Book”)
Parsing Calculate grammatical structure of program, like diagramming sentences, where: Tokens = “words” Programs = “sentences” For further information, read: Aho, Sethi, Ullman, “Compilers: Principles, Techniques, and Tools” (a. k. a, the “Dragon Book”)
 Outline of coverage l Context-free grammars l Parsing – Tabular Parsing Methods – One pass • Top-down • Bottom-up l Yacc
Outline of coverage l Context-free grammars l Parsing – Tabular Parsing Methods – One pass • Top-down • Bottom-up l Yacc
 Parser: extracts grammatical structure of program function-def name arguments stmt-list stmt main expression operator expression variable << string cout “hello, worldn”
Parser: extracts grammatical structure of program function-def name arguments stmt-list stmt main expression operator expression variable << string cout “hello, worldn”
 Context-free languages Grammatical structure defined by contextfree grammar statement labeled-statement | expression-statement | compound-statement labeled-statement ident : statement | case constant-expression : statement compound-statement { declaration-list statement-list } “Context-free” = only one non-terminal in left-part terminal non-terminal
Context-free languages Grammatical structure defined by contextfree grammar statement labeled-statement | expression-statement | compound-statement labeled-statement ident : statement | case constant-expression : statement compound-statement { declaration-list statement-list } “Context-free” = only one non-terminal in left-part terminal non-terminal
 Parse trees Parse tree = tree labeled with grammar symbols, such that: l If node is labeled A, and its children are labeled x 1. . . xn, then there is a production A x 1. . . xn l “Parse tree from A” = root labeled with A l “Complete parse tree” = all leaves labeled with tokens
Parse trees Parse tree = tree labeled with grammar symbols, such that: l If node is labeled A, and its children are labeled x 1. . . xn, then there is a production A x 1. . . xn l “Parse tree from A” = root labeled with A l “Complete parse tree” = all leaves labeled with tokens
 Parse trees and sentences Frontier of tree = labels on leaves (in left-to -right order) l Frontier of tree from S is a sentential form l Frontier of a complete tree from S is a sentence l L E a L ; E “Frontier”
Parse trees and sentences Frontier of tree = labels on leaves (in left-to -right order) l Frontier of tree from S is a sentential form l Frontier of a complete tree from S is a sentence l L E a L ; E “Frontier”
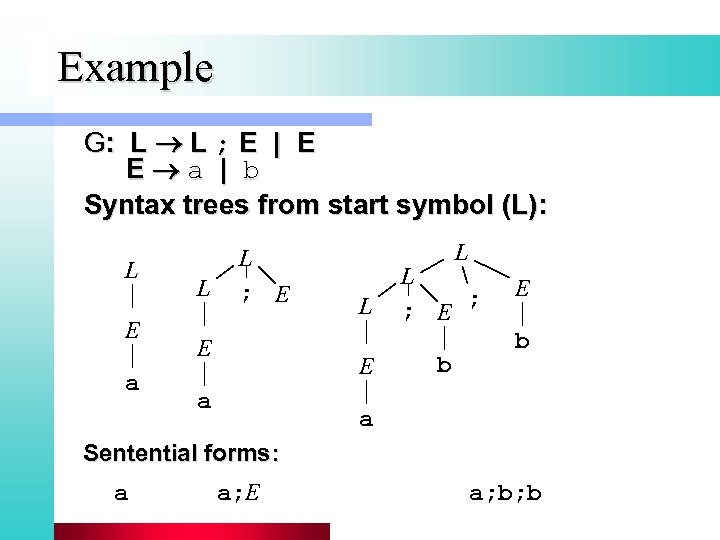 Example G: L L ; E | E E a | b Syntax trees from start symbol (L): L E a L L ; E E L L E a L ; E ; b E b a Sentential forms: a a; E a; b; b
Example G: L L ; E | E E a | b Syntax trees from start symbol (L): L E a L L ; E E L L E a L ; E ; b E b a Sentential forms: a a; E a; b; b
 Derivations Alternate definition of sentence: l Given , in V*, say is a derivation step if ’ ’’ and = ’ ’’ , where A is a production l is a sentential form iff there exists a derivation (sequence of derivation steps) S ( alternatively, we say that S * ) Two definitions are equivalent, but note that there are many derivations corresponding to each parse tree
Derivations Alternate definition of sentence: l Given , in V*, say is a derivation step if ’ ’’ and = ’ ’’ , where A is a production l is a sentential form iff there exists a derivation (sequence of derivation steps) S ( alternatively, we say that S * ) Two definitions are equivalent, but note that there are many derivations corresponding to each parse tree
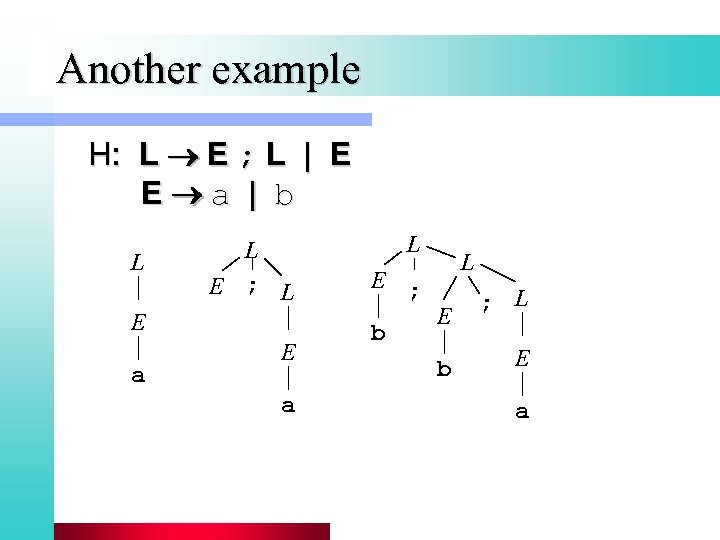 Another example H: L E ; L | E E a | b L L E ; L E a L E ; b L E b ; L E a
Another example H: L E ; L | E E a | b L L E ; L E a L E ; b L E b ; L E a
 Ambiguity For some purposes, it is important to know whether a sentence can have more than one parse tree l A grammar is ambiguous if there is a sentence with more than one parse tree l Example: E E+E | E*E | id l E E E + E id E * id E E E id id + * E E id id
Ambiguity For some purposes, it is important to know whether a sentence can have more than one parse tree l A grammar is ambiguous if there is a sentence with more than one parse tree l Example: E E+E | E*E | id l E E E + E id E * id E E E id id + * E E id id
 l If e then if b then d else f l { int x; y = 0; } l A. b. c = d; l Id -> s | s. id E -> E + T + T -> id + T -> id + T * id + T -> id + id * id + id
l If e then if b then d else f l { int x; y = 0; } l A. b. c = d; l Id -> s | s. id E -> E + T + T -> id + T -> id + T * id + T -> id + id * id + id
 Ambiguity l Ambiguity is a function of the grammar rather than the language l Certain ambiguous grammars may have equivalent unambiguous ones
Ambiguity l Ambiguity is a function of the grammar rather than the language l Certain ambiguous grammars may have equivalent unambiguous ones
 Grammar Transformations l Grammars can be transformed without affecting the language generated l Three transformations are discussed next: – Eliminating Ambiguity – Eliminating Left Recursion (i. e. productions of the form A A ) – Left Factoring
Grammar Transformations l Grammars can be transformed without affecting the language generated l Three transformations are discussed next: – Eliminating Ambiguity – Eliminating Left Recursion (i. e. productions of the form A A ) – Left Factoring
 Eliminating Ambiguity Sometimes an ambiguous grammar can be rewritten to eliminate ambiguity l For example, expressions involving additions and products can be written as follows: l E E +T | T T T*id | id The language generated by this grammar is the same as that generated by the grammar on tranparency 11. Both generate id(+id|*id)* l However, this grammar is not ambiguous l
Eliminating Ambiguity Sometimes an ambiguous grammar can be rewritten to eliminate ambiguity l For example, expressions involving additions and products can be written as follows: l E E +T | T T T*id | id The language generated by this grammar is the same as that generated by the grammar on tranparency 11. Both generate id(+id|*id)* l However, this grammar is not ambiguous l
 Eliminating Ambiguity (Cont. ) l One advantage of this grammar is that it represents the precedence between operators. In the parsing tree, products appear nested within additions E E T id + T T * id id
Eliminating Ambiguity (Cont. ) l One advantage of this grammar is that it represents the precedence between operators. In the parsing tree, products appear nested within additions E E T id + T T * id id
 Eliminating Ambiguity (Cont. ) l An example of ambiguity in a programming language is the dangling else l Consider S if then S else S | if then S|
Eliminating Ambiguity (Cont. ) l An example of ambiguity in a programming language is the dangling else l Consider S if then S else S | if then S|
 Eliminating Ambiguity (Cont. ) l When there are two nested ifs and only one else. . S if then S S else if then S S if S then if then S else S
Eliminating Ambiguity (Cont. ) l When there are two nested ifs and only one else. . S if then S S else if then S S if S then if then S else S
 Eliminating Ambiguity (Cont. ) l In most languages (including C++ and Java), each else is assumed to belong to the nearest if that is not already matched by an else. This association is expressed in the following (unambiguous) grammar: S Matched | Unmatched Matched if then Matched else Matched | Unmatched if then S | if then Matched else Unmatched
Eliminating Ambiguity (Cont. ) l In most languages (including C++ and Java), each else is assumed to belong to the nearest if that is not already matched by an else. This association is expressed in the following (unambiguous) grammar: S Matched | Unmatched Matched if then Matched else Matched | Unmatched if then S | if then Matched else Unmatched
 Eliminating Ambiguity (Cont. ) l Ambiguity is a property of the grammar l It is undecidable whether a context free grammar is ambiguous l The proof is done by reduction to Post’s correspondence problem l Although there is no general algorithm, it is possible to isolate certain constructs in productions which lead to ambiguous grammars
Eliminating Ambiguity (Cont. ) l Ambiguity is a property of the grammar l It is undecidable whether a context free grammar is ambiguous l The proof is done by reduction to Post’s correspondence problem l Although there is no general algorithm, it is possible to isolate certain constructs in productions which lead to ambiguous grammars
 Eliminating Ambiguity (Cont. ) l For example, a grammar containing the production A AA | would be ambiguous, because the substring has two parses: A A A l A A A A A This ambiguity disappears if we use the productions A AB | B and B or the productions A BA | B and B .
Eliminating Ambiguity (Cont. ) l For example, a grammar containing the production A AA | would be ambiguous, because the substring has two parses: A A A l A A A A A This ambiguity disappears if we use the productions A AB | B and B or the productions A BA | B and B .
 Eliminating Ambiguity (Cont. ) l Examples of ambiguous productions: A A A | A and A A | A A language generated by an ambiguous CFG is inherently ambiguous if it has no unambiguous CFG – An example of such a language is L={aibjcm | i=j or j=m} which can be generated by the grammar: S AB | DC A a. A | C c. C | B b. Bc | D a. Db |
Eliminating Ambiguity (Cont. ) l Examples of ambiguous productions: A A A | A and A A | A A language generated by an ambiguous CFG is inherently ambiguous if it has no unambiguous CFG – An example of such a language is L={aibjcm | i=j or j=m} which can be generated by the grammar: S AB | DC A a. A | C c. C | B b. Bc | D a. Db |
 Elimination of Left Recursion l A grammar is left recursive if it has a nonterminal A and a derivation A +A for some string Top-down parsing methods (to be discussed shortly) cannot handle left-recursive grammars, so a transformation to eliminate left recursion is needed. l Immediate left recursion (productions of the form A A ) can be easily eliminated. l We group the A-productions as A A 1 | A 2 | … | A m | 1| 2 | … | n where no i begins with A. Then we replace the Aproductions by A 1 A’ | 2 A’ | … | n A’ A’ 1 A’ | 2 A’| … | m A’ |
Elimination of Left Recursion l A grammar is left recursive if it has a nonterminal A and a derivation A +A for some string Top-down parsing methods (to be discussed shortly) cannot handle left-recursive grammars, so a transformation to eliminate left recursion is needed. l Immediate left recursion (productions of the form A A ) can be easily eliminated. l We group the A-productions as A A 1 | A 2 | … | A m | 1| 2 | … | n where no i begins with A. Then we replace the Aproductions by A 1 A’ | 2 A’ | … | n A’ A’ 1 A’ | 2 A’| … | m A’ |
 Elimination of Left Recursion (Cont. ) l The previous transformation, however, does not eliminate left recursion involving two or more steps. For example, consider the grammar S Aa | b A Ac| Sd |e S is left-recursive because S Aa Sda, but it is not immediately left recursive
Elimination of Left Recursion (Cont. ) l The previous transformation, however, does not eliminate left recursion involving two or more steps. For example, consider the grammar S Aa | b A Ac| Sd |e S is left-recursive because S Aa Sda, but it is not immediately left recursive
 Elimination of Left Recursion (Cont. ) Algorithm. Eliminate left recursion Arrange nonterminals in some order A 1, A 2 , , …, An for i =1 to n { for j =1 to i -1 { replace each production of the form Ai Aj g by the production Ai d 1 g | d 2 g | … | dn g where Aj d 1 | d 2 |…| dn are all the current Ajproductions } eliminate the immediate left recursion among the Aiproductions }
Elimination of Left Recursion (Cont. ) Algorithm. Eliminate left recursion Arrange nonterminals in some order A 1, A 2 , , …, An for i =1 to n { for j =1 to i -1 { replace each production of the form Ai Aj g by the production Ai d 1 g | d 2 g | … | dn g where Aj d 1 | d 2 |…| dn are all the current Ajproductions } eliminate the immediate left recursion among the Aiproductions }
 Elimination of Left Recursion (Cont. ) To show that the previous algorithm actually works all we need notice is that iteration i only changes productions with Ai on the left-hand side. And m > i in all productions of the form Ai Am l Induction proof: l – Clearly true for i=1 – If it is true for all i
Elimination of Left Recursion (Cont. ) To show that the previous algorithm actually works all we need notice is that iteration i only changes productions with Ai on the left-hand side. And m > i in all productions of the form Ai Am l Induction proof: l – Clearly true for i=1 – If it is true for all i
 Left Factoring l l Left factoring helps transform a grammar for predictive parsing For example, if we have the two productions S if then S else S | if then S on seeing the input token if, we cannot immediately tell which production to choose to expand S In general, if we have A 1 | 2 and the input begins with , we do not know (without looking further) which production to use to expand A
Left Factoring l l Left factoring helps transform a grammar for predictive parsing For example, if we have the two productions S if then S else S | if then S on seeing the input token if, we cannot immediately tell which production to choose to expand S In general, if we have A 1 | 2 and the input begins with , we do not know (without looking further) which production to use to expand A
 Left Factoring (Cont. ) l However, we may defer the decision by expanding A to A’ l Then after seeing the input derived from , we may expand A’ to 1 or to 2 l Left-factored, the original productions become A A’ A’ 1 | 2
Left Factoring (Cont. ) l However, we may defer the decision by expanding A to A’ l Then after seeing the input derived from , we may expand A’ to 1 or to 2 l Left-factored, the original productions become A A’ A’ 1 | 2
 Non-Context-Free Language Constructs l Examples of non-context-free languages are: – L 1 = {wcw | w is of the form (a|b)*} – L 2 = {anbmcndm | n 1 and m 1 } – L 3 = {anbncn | n 0 } l Languages similar to these that are context free – L’ 1 = {wcw. R | w is of the form (a|b)*} (w. R stands for w reversed) This language is generated by the grammar S a. Sa | b. Sb | c – L’ 2 = {anbmcmdn | n 1 and m 1 } This language is generated by the grammar S a. Sd | a. Ad A b. Ac | bc
Non-Context-Free Language Constructs l Examples of non-context-free languages are: – L 1 = {wcw | w is of the form (a|b)*} – L 2 = {anbmcndm | n 1 and m 1 } – L 3 = {anbncn | n 0 } l Languages similar to these that are context free – L’ 1 = {wcw. R | w is of the form (a|b)*} (w. R stands for w reversed) This language is generated by the grammar S a. Sa | b. Sb | c – L’ 2 = {anbmcmdn | n 1 and m 1 } This language is generated by the grammar S a. Sd | a. Ad A b. Ac | bc
 Non-Context-Free Language Constructs (Cont. ) l L” 2={anbncmdm | n 1 and m 1 } is generated by the grammar S AB A a. Ab | ab B c. Bd | cd l L’ 3={anbn | n 1} is generated by the grammar S a. Sb | ab This language is not definable by any regular expression
Non-Context-Free Language Constructs (Cont. ) l L” 2={anbncmdm | n 1 and m 1 } is generated by the grammar S AB A a. Ab | ab B c. Bd | cd l L’ 3={anbn | n 1} is generated by the grammar S a. Sb | ab This language is not definable by any regular expression
 Non-Context-Free Language Constructs (Cont. ) l l l Suppose we could construct a DFSM D accepting L’ 3. D must have a finite number of states, say k. Consider the sequence of states s 0, s 1, s 2, …, sk entered by D having read , a, aa, …, ak. Since D only has k states, two of the states in the sequence have to be equal. Say, si sj (i j). From si, a sequence of i bs leads to an accepting (final) state. Therefore, the same sequence of i bs will also lead to an accepting state from sj. Therefore D would accept ajbi which means that the language accepted by D is not identical to L’ 3. A contradiction.
Non-Context-Free Language Constructs (Cont. ) l l l Suppose we could construct a DFSM D accepting L’ 3. D must have a finite number of states, say k. Consider the sequence of states s 0, s 1, s 2, …, sk entered by D having read , a, aa, …, ak. Since D only has k states, two of the states in the sequence have to be equal. Say, si sj (i j). From si, a sequence of i bs leads to an accepting (final) state. Therefore, the same sequence of i bs will also lead to an accepting state from sj. Therefore D would accept ajbi which means that the language accepted by D is not identical to L’ 3. A contradiction.
 Parsing The parsing problem is: Given string of tokens w, find a parse tree whose frontier is w. (Equivalently, find a derivation from w. ) A parser for a grammar G reads a list of tokens and finds a parse tree if they form a sentence (or reports an error otherwise) Two classes of algorithms for parsing: – Top-down – Bottom-up
Parsing The parsing problem is: Given string of tokens w, find a parse tree whose frontier is w. (Equivalently, find a derivation from w. ) A parser for a grammar G reads a list of tokens and finds a parse tree if they form a sentence (or reports an error otherwise) Two classes of algorithms for parsing: – Top-down – Bottom-up
 Parser generators A parser generator is a program that reads a grammar and produces a parser l The best known parser generator is yacc It produces bottom-up parsers l Most parser generators - including yacc do not work for every CFG; they accept a restricted class of CFG’s that can be parsed efficiently using the method employed by that parser generator l
Parser generators A parser generator is a program that reads a grammar and produces a parser l The best known parser generator is yacc It produces bottom-up parsers l Most parser generators - including yacc do not work for every CFG; they accept a restricted class of CFG’s that can be parsed efficiently using the method employed by that parser generator l
 Top-down parsing l Starting from parse tree containing just S, build tree down toward input. Expand left-most non-terminal. l Algorithm: (next slide)
Top-down parsing l Starting from parse tree containing just S, build tree down toward input. Expand left-most non-terminal. l Algorithm: (next slide)
 Top-down parsing (cont. ) l Let input = a 1 a 2. . . an current sentential form (csf) = S loop { suppose csf = t 1. . . tk. A if t 1. . . tk a 1. . . ak , it’s an error based on ak+1. . . , choose production A csf becomes t 1. . . tk }
Top-down parsing (cont. ) l Let input = a 1 a 2. . . an current sentential form (csf) = S loop { suppose csf = t 1. . . tk. A if t 1. . . tk a 1. . . ak , it’s an error based on ak+1. . . , choose production A csf becomes t 1. . . tk }
 Top-down parsing example Grammar: H: L E ; L | E E a | b Input: a; b Parse tree Sentential form L L E ; L a Input L E; L a; b a; L a; b
Top-down parsing example Grammar: H: L E ; L | E E a | b Input: a; b Parse tree Sentential form L L E ; L a Input L E; L a; b a; L a; b
 Top-down parsing example (cont. ) Parse tree L E ; L a E b Input a; E a; b E L E ; L a Sentential form
Top-down parsing example (cont. ) Parse tree L E ; L a E b Input a; E a; b E L E ; L a Sentential form
 LL(1) parsing l Efficient form of top-down parsing l Use only first symbol of remaining input (ak+1) to choose next production. That is, employ a function M: N P in “choose production” step of algorithm. l When this works, grammar is called LL(1)
LL(1) parsing l Efficient form of top-down parsing l Use only first symbol of remaining input (ak+1) to choose next production. That is, employ a function M: N P in “choose production” step of algorithm. l When this works, grammar is called LL(1)
 LL(1) examples l Example 1: H: L E ; L | E E a | b Given input a; b, so next symbol is a. Which production to use? Can’t tell. H not LL(1)
LL(1) examples l Example 1: H: L E ; L | E E a | b Given input a; b, so next symbol is a. Which production to use? Can’t tell. H not LL(1)
 LL(1) examples l Example 2: Exp Term Exp’ $ | + Exp Term id (Use $ for “end-of-input” symbol. ) Grammar is LL(1): Exp and Term have only one production; Exp’ has two productions but only one is applicable at any time.
LL(1) examples l Example 2: Exp Term Exp’ $ | + Exp Term id (Use $ for “end-of-input” symbol. ) Grammar is LL(1): Exp and Term have only one production; Exp’ has two productions but only one is applicable at any time.
 Nonrecursive predictive parsing l It is possible to build a nonrecursive predictive parser by maintaining a stack explicitly, rather than implicitly via recursive calls l The key problem during predictive parsing is that of determining the production to be applied for a nonterminal
Nonrecursive predictive parsing l It is possible to build a nonrecursive predictive parser by maintaining a stack explicitly, rather than implicitly via recursive calls l The key problem during predictive parsing is that of determining the production to be applied for a nonterminal
 Nonrecursive predictive parsing Algorithm. Nonrecursive predictive parsing Set ip to point to the first symbol of w$. repeat Let X be the top of the stack symbol and a the symbol pointed to by ip if X is a terminal or $ then if X == a then pop X from the stack and advance ip else error() else // X is a nonterminal if M[X, a] == X Y 1 Y 2 … Y k then pop X from the stack push Yk. Y k-1, …, Y 1 onto the stack with Y 1 on top (push nothing if Y 1 Y 2 … Y k is ) output the production X Y 1 Y 2 … Y k else error() until X == $
Nonrecursive predictive parsing Algorithm. Nonrecursive predictive parsing Set ip to point to the first symbol of w$. repeat Let X be the top of the stack symbol and a the symbol pointed to by ip if X is a terminal or $ then if X == a then pop X from the stack and advance ip else error() else // X is a nonterminal if M[X, a] == X Y 1 Y 2 … Y k then pop X from the stack push Yk. Y k-1, …, Y 1 onto the stack with Y 1 on top (push nothing if Y 1 Y 2 … Y k is ) output the production X Y 1 Y 2 … Y k else error() until X == $
 LL(1) grammars l No left recursion A A : If this production is chosen, parse makes no progress. l No common prefixes A | Can fix by “left factoring”: A A’ ’ |
LL(1) grammars l No left recursion A A : If this production is chosen, parse makes no progress. l No common prefixes A | Can fix by “left factoring”: A A’ ’ |
 LL(1) grammars (cont. ) l No ambiguity Precise definition requires that production to choose be unique (“choose” function M very hard to calculate otherwise)
LL(1) grammars (cont. ) l No ambiguity Precise definition requires that production to choose be unique (“choose” function M very hard to calculate otherwise)
 Top-down Parsing L Input tokens:
Top-down Parsing L Input tokens:
 Checking LL(1)-ness l For any sequence of grammar symbols , define set FIRST( ) to be FIRST( ) = { a | * a for some }
Checking LL(1)-ness l For any sequence of grammar symbols , define set FIRST( ) to be FIRST( ) = { a | * a for some }
 Checking LL(1)-ness l Define: Grammar G = (N, , P, S) is LL(1) iff whenever there are two left-most derivations (in which the leftmost nonterminal is always expanded first) S =>* w. A => w =>* wx S =>* w. A => w =>* wy such that FIRST(x) = FIRST(y), it follows that = In other words, given 1. A string w. A in V* and 2. The first terminal symbol to be derived from A , say t there is at most one production that can be applied to A to yield a derivation of any terminal string beginning with wt l FIRST sets can often be calculated by inspection
Checking LL(1)-ness l Define: Grammar G = (N, , P, S) is LL(1) iff whenever there are two left-most derivations (in which the leftmost nonterminal is always expanded first) S =>* w. A => w =>* wx S =>* w. A => w =>* wy such that FIRST(x) = FIRST(y), it follows that = In other words, given 1. A string w. A in V* and 2. The first terminal symbol to be derived from A , say t there is at most one production that can be applied to A to yield a derivation of any terminal string beginning with wt l FIRST sets can often be calculated by inspection
 FIRST Sets Exp Term Exp’ $ | + Exp Term id (Use $ for “end-of-input” symbol) FIRST($) = {$} FIRST(+ Exp) = {+} FIRST($) FIRST(+ Exp) = {} grammar is LL(1)
FIRST Sets Exp Term Exp’ $ | + Exp Term id (Use $ for “end-of-input” symbol) FIRST($) = {$} FIRST(+ Exp) = {+} FIRST($) FIRST(+ Exp) = {} grammar is LL(1)
 FIRST Sets L E ; L | E E a | b FIRST(E ; L) = {a, b} = FIRST(E) FIRST(E ; L) FIRST(E) {} grammar not LL(1).
FIRST Sets L E ; L | E E a | b FIRST(E ; L) = {a, b} = FIRST(E) FIRST(E ; L) FIRST(E) {} grammar not LL(1).
 Computing FIRST Sets Algorithm. Compute FIRST(X) for all grammar symbols X forall X V do FIRST(X)={} forall X (X is a terminal) do FIRST(X)={X} forall productions X do FIRST(X) = FIRST(X) U { } repeat c: forall productions X Y 1 Y 2 … Y k do forall i [1, k] do FIRST(X) = FIRST(X) U (FIRST(Yi) - { }) if FIRST(Yi) then continue c FIRST(X) = FIRST(X) U { } until no more terminals or are added to any FIRST set
Computing FIRST Sets Algorithm. Compute FIRST(X) for all grammar symbols X forall X V do FIRST(X)={} forall X (X is a terminal) do FIRST(X)={X} forall productions X do FIRST(X) = FIRST(X) U { } repeat c: forall productions X Y 1 Y 2 … Y k do forall i [1, k] do FIRST(X) = FIRST(X) U (FIRST(Yi) - { }) if FIRST(Yi) then continue c FIRST(X) = FIRST(X) U { } until no more terminals or are added to any FIRST set
 FIRST Sets of Strings of Symbols l FIRST(X 1 X 2…Xn) is the union of FIRST(X 1) and all FIRST(Xi) such that FIRST(Xk) for k=1, 2, …, i-1 l FIRST(X 1 X 2…Xn) contains iff FIRST(Xk) for k=1, 2, …, n
FIRST Sets of Strings of Symbols l FIRST(X 1 X 2…Xn) is the union of FIRST(X 1) and all FIRST(Xi) such that FIRST(Xk) for k=1, 2, …, i-1 l FIRST(X 1 X 2…Xn) contains iff FIRST(Xk) for k=1, 2, …, n
 FIRST Sets do not Suffice l Given the productions A T x A T y T w T l T w should be applied when the next input token is w. l T should be applied whenever the next terminal (the one pointed to by ip) is either x or y
FIRST Sets do not Suffice l Given the productions A T x A T y T w T l T w should be applied when the next input token is w. l T should be applied whenever the next terminal (the one pointed to by ip) is either x or y
 FOLLOW Sets l For any nonterminal X, define set FOLLOW(X) as FOLLOW(X) = {a | S * Xa }
FOLLOW Sets l For any nonterminal X, define set FOLLOW(X) as FOLLOW(X) = {a | S * Xa }
 Computing the FOLLOW Set Algorithm. Compute FOLLOW(X) for all nonterminals X FOLLOW(S) ={$} forall productions A B do FOLLOW(B)=Follow(B) U (FIRST( ) - { }) repeat forall productions A B or A B with FIRST( ) do FOLLOW(B) = FOLLOW(B) U FOLLOW(A) until all FOLLOW sets remain the same
Computing the FOLLOW Set Algorithm. Compute FOLLOW(X) for all nonterminals X FOLLOW(S) ={$} forall productions A B do FOLLOW(B)=Follow(B) U (FIRST( ) - { }) repeat forall productions A B or A B with FIRST( ) do FOLLOW(B) = FOLLOW(B) U FOLLOW(A) until all FOLLOW sets remain the same
 Construction of a predictive parsing table Algorithm. Construction of a predictive parsing table M[: , : ] = {} forall productions A do forall a FIRST( ) do M[A, a] = M[A, a] U {A } if FIRST( ) then forall b FOLLOW(A) do M[A, b] = M[A, b] U {A } Make all empty entries of M be error
Construction of a predictive parsing table Algorithm. Construction of a predictive parsing table M[: , : ] = {} forall productions A do forall a FIRST( ) do M[A, a] = M[A, a] U {A } if FIRST( ) then forall b FOLLOW(A) do M[A, b] = M[A, b] U {A } Make all empty entries of M be error
 Another Definition of LL(1) Define: Grammar G is LL(1) if for every A N with productions A 1 | | n FIRST( i FOLLOW(A)) FIRST( j FOLLOW(A) ) = for all i, j
Another Definition of LL(1) Define: Grammar G is LL(1) if for every A N with productions A 1 | | n FIRST( i FOLLOW(A)) FIRST( j FOLLOW(A) ) = for all i, j
 Regular Languages l Definition. A regular grammar is one whose productions are all of the type: – A a. B – A a l A Regular Expression is either: –a – R 1 | R 2 – R 1 R 2 – R*
Regular Languages l Definition. A regular grammar is one whose productions are all of the type: – A a. B – A a l A Regular Expression is either: –a – R 1 | R 2 – R 1 R 2 – R*
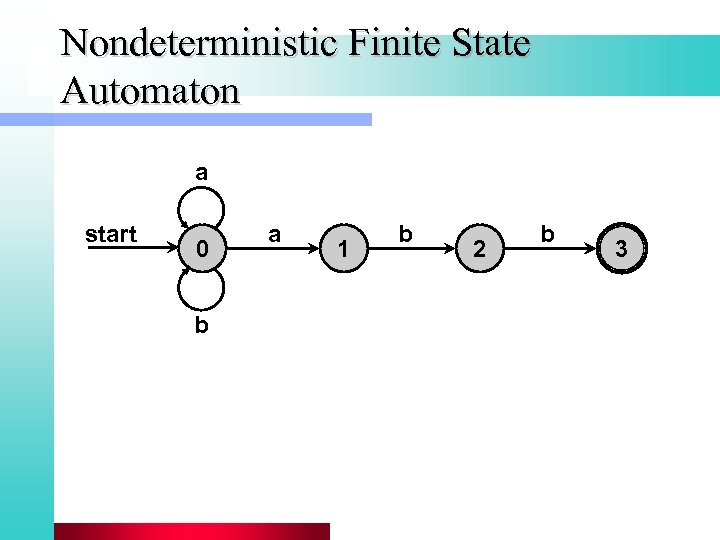 Nondeterministic Finite State Automaton a start 0 b a 1 b 2 b 3
Nondeterministic Finite State Automaton a start 0 b a 1 b 2 b 3
 Regular Languages l Theorem. The classes of languages – Generated by a regular grammar – Expressed by a regular expression – Recognized by a NDFS automaton – Recognized by a DFS automaton coincide.
Regular Languages l Theorem. The classes of languages – Generated by a regular grammar – Expressed by a regular expression – Recognized by a NDFS automaton – Recognized by a DFS automaton coincide.
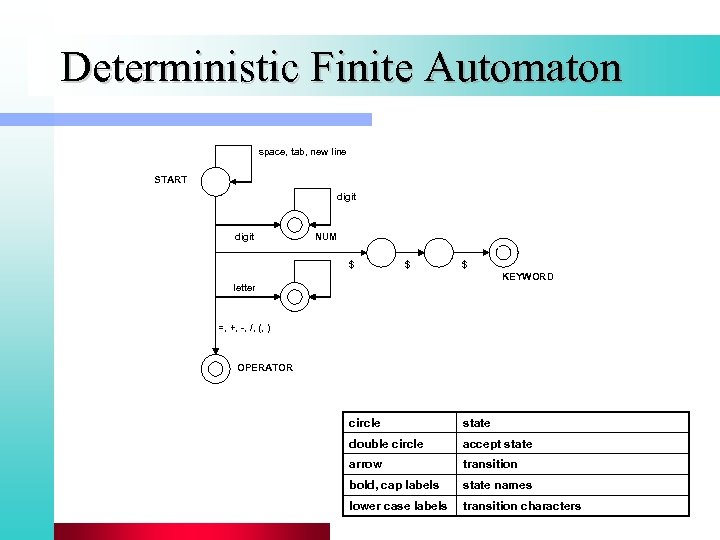 Deterministic Finite Automaton space, tab, new line START digit NUM $ $ $ KEYWORD letter =, +, -, /, (, ) OPERATOR circle state double circle accept state arrow transition bold, cap labels state names lower case labels transition characters
Deterministic Finite Automaton space, tab, new line START digit NUM $ $ $ KEYWORD letter =, +, -, /, (, ) OPERATOR circle state double circle accept state arrow transition bold, cap labels state names lower case labels transition characters
 Scanner code state : = start loop if no input character buffered then read one, and add it to the accumulated token case state of start: case input_char of A. . Z, a. . z : state : = id 0. . 9 : state : = num else. . . end id: case input_char of A. . Z, a. . z : state : = id 0. . 9 : state : = id else. . . end num: case input_char of 0. . 9: . . . else. . . end;
Scanner code state : = start loop if no input character buffered then read one, and add it to the accumulated token case state of start: case input_char of A. . Z, a. . z : state : = id 0. . 9 : state : = num else. . . end id: case input_char of A. . Z, a. . z : state : = id 0. . 9 : state : = id else. . . end num: case input_char of 0. . 9: . . . else. . . end;
 Table-driven DFA 0 -start 1 -num 2 -id 3 -operator 4 -keyword white space 0 exit letter 2 error 2 exit error digit 1 1 2 exit error operator 3 exit $ 4 error exit 4
Table-driven DFA 0 -start 1 -num 2 -id 3 -operator 4 -keyword white space 0 exit letter 2 error 2 exit error digit 1 1 2 exit error operator 3 exit $ 4 error exit 4
![Language Classes L 0 CSL CFL [NPA] LR(1) LL(1) RL [DFA=NFA] Language Classes L 0 CSL CFL [NPA] LR(1) LL(1) RL [DFA=NFA]](https://present5.com/presentation/4976d7a18b0ad000e265ea91891a8f58/image-63.jpg) Language Classes L 0 CSL CFL [NPA] LR(1) LL(1) RL [DFA=NFA]
Language Classes L 0 CSL CFL [NPA] LR(1) LL(1) RL [DFA=NFA]
 Question l Are regular expressions, as provided by Perl or other languages, sufficient for parsing nested structures, e. g. XML files?
Question l Are regular expressions, as provided by Perl or other languages, sufficient for parsing nested structures, e. g. XML files?


