От степени варьирования признака – зависимость прямая. Если

От степени варьирования признака – зависимость прямая. Если признак не варьирует, то есть у всех еди-ниц совокупности одинаковые значения признака, то ошибка выборки будет равна 0. Отсюда увеличение колюблемости признака влечет увеличение ошибки выборки. Зависимость ошибки выборки от рассмотрен-ных факторов может быть выражена следующей формулой:

СТАНДАРТНАЯ ОШИБКА ВЫБОРКИ где – μ – стандартная (средняя) ошибка выборки; σ2 – дисперсия количественного признака; n – численность выборки; ω(1- ω) – дисперсия альтернативного признака. Количественный признак Альтернативный признак

Под СТАНДАРТНОЙ ОШИБКОЙ ВЫБОРКИ понимают такое расхождение между генеральными и выборочными характеристиками, которое не превы-шает ± σ. (х - х) ≤ ± σ Формулы СТАНДАРТНОЙ ОШИБКИ при бесповторном отборе. Количественный признак Альтернативный признак

Стандартная ошибка позволяет определить ПРЕДЕЛЬНУЮ ОШИБКУ (Δ), то есть максимально возможное расхождение между генеральной и выборочной характеристиками. Предельная ошибка определяется по формуле:. где t - заданный коэффициент доверия или коэффициент кратности ошибки. Определяется по таблице интегральной функции Лапласа и зависит от вероятности с которой можно гарантировать, что предельная ошибка не превысит стандартную в t - раз.

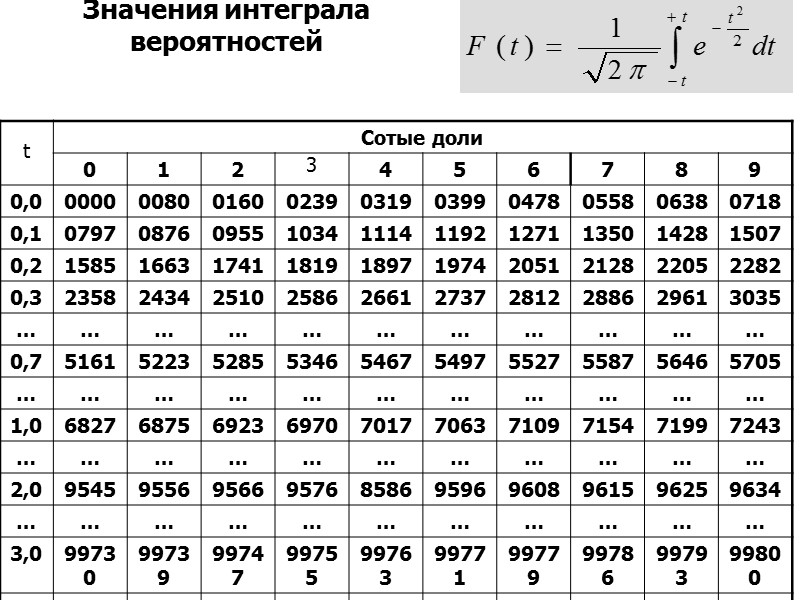
Значения интеграла вероятностей

Например: При вероятности ρ = 0,683 → t = 1; При вероятности ρ = 0,954 → t =2; При вероятности ρ = 0,997 → t = 3. Предположим, что t=2, следовательно, с вероят-ностью 0,954 мы можем гарантировать, что в 95,4 случаях из 100 (или в 954 случаях из 1000) ошибка репрезентативности не превысит ±2μ. То есть в 954 случаях из 1000 характеристики генеральной совокупности будут отличаться от характеристик выборочной совокупности не более чем на 2μ. Но в остальных 46 случаях (1000-954) они будут отличаться и на большее значение.

Предельная ошибка позволяет определить ДОВЕРИ-ТЕЛЬНЫЙ ИНТЕРВАЛ для характеристик генеральной совокупности. ОПРЕДЕЛЕНИЕ: Доверительным называется интервал, который покрывает неизвестный параметр с заданной надежностью. Определяется по формуле: Количественный признак Альтернативный признак

ОТНОСИТЕЛЬНАЯ ОШИБКА ВЫБОРКИ представляет собой отношение стандартной ошибки выборки к соответствующей характеристике выборочной совокупности, выраженное в процентах . Если Р < 5 %, то полученные среднюю величину и долю можно использовать для характеристики изучаемого признака. Если Р > 5 %, то данные характеристики не рекомендуется использовать для прогноза.

При типическом отборе величина стандартной ошибки зависит от средней из групповых дисперсий: - повторный отбор - бесповторный отбор При серийном отборе величина стандартной ошибки зависит от межгрупповой дисперсии: При комбинированном отборе величина стандартной ошибки определяется ступенчатостью отбора: где μ12, μ22, μ32 – стандартные ошибки каждого вида выборки.

4. Определение необходимой численности выборки ФОРМУЛЫ НЕОБХОДИМОЙ ЧИСЛЕННОСТИ ВЫБОРКИ: Количественный признак - повторный отбор - бесповторный отбор → →

4. Определение необходимой численности выборки ФОРМУЛЫ НЕОБХОДИМОЙ ЧИСЛЕННОСТИ ВЫБОРКИ: Альтернативный признак - повторный отбор - бесповторный отбор → →

Для определения численности выборки по этим формулам необходимо знать дисперсию (σ2) и предельную ошибку выборки (Δ), то есть то, что мы знать не можем пока не проведем выборку. Поэтому, на практике заранее обговаривается величина предельной ошибки (то есть, чтобы предельная ошибка не превышала заданных размеров).

5. Малая выборка. Малая выборка - это выборка численность которой находится в пределах от 5 до 30 единиц. Особенность малой выборки состоит в том, что её случайные ошибки не подчиняются закону нормального распределения, а соответствуют РАСПРЕДЕЛЕНИЮ СТЬЮДЕНТА. Кривая Стьюдента, как и нормального распределения, симметрична относительно точки t=0, но она более полога и её ординаты медленнее приближаются к оси абсцисс.

Стандартная ошибка малой выборки определяется по формуле: Однако величина t здесь иная и связана не только с вероятностной оценкой, но и с численностью выборки, вернее с числом степеней свободы: k = n-1 где Предельная ошибка малой выборки имеет обычный вид^

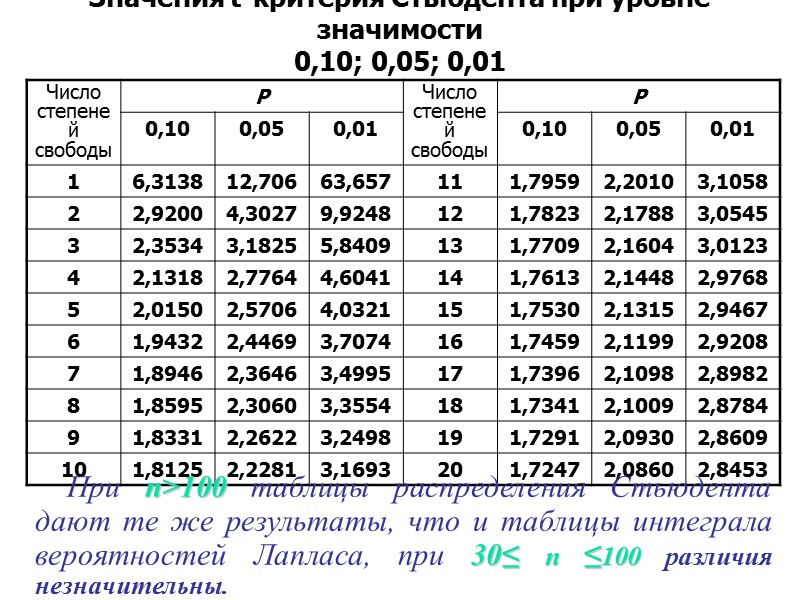
Значения t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01 При n>100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30≤ n ≤100 различия незначительны.

СТАТИСТИЧЕСКОЙ ОЦЕНКОЙ неизвестного параметра генеральной совокупности называют случайную величину, по лученную на основании исследова- ния выборочной совокупности. Чтобы оцениваемы параметры были точны (достоверны) необходимо, чтобы их статистические оценки были несмещенные, эффективные и состоятельные. НЕСМЕЩЕННОЙ называют такую статистическую оценку неизвестного параметра, математическое ожидание которой равно оцениваемому параметру. 6. Статистическая оценка параметров распределения

6. Статистическая оценка параметров распределения ЭФФЕКТИВНОЙ называют статистическую оценку, обладающую наименьшей дисперсией. Если n велико, то возникает требование состоятельности оценки. СОСТОЯТЕЛЬНОЙ называют статистическую оценку, которая при увеличении численности выборочной совокупности (при n → ∞) стремиться по вероятности к оцениваемому параметру.

6. Статистическая оценка параметров распределения ТОЧЕЧНОЙ называют оценку, которая определяется одним числом. ИНТЕРВАЛЬНОЙ называют оценку, которая определяется двумя числами – концами интервала. Точечной, несмещенной и состоятельной оценкой генеральной средней является выборочная средняя, а генеральной доли – выборочная доля: х = х; ω = р Чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной средней (или выборочная доля - от генеральной доли).

6. Статистическая оценка параметров распределения Для определения интервальной оценки необходимо найти доверительные интервалы, покрывающие оцениваемый параметр с заданной надежностью: Надежность указывает (например, α=0,95), что при достаточно большом числе наблюдений в 95-ти случаях из 100 оцениваемый параметр будет действительно заключен в найденных доверительных интервалах и лишь в 5 случаях он может выйти за границы доверительных интервалов.

7. Оценка достоверности выборочных характеристик ДОСТОВЕРНОСТЬ любого параметра оценивается по критерию достоверности, определяемому как отношение оцениваемого параметра к его ошибке. Вычислим критерий достоверности для выборочной средней: Сравним фактическое значение tx с критическим, определенным по таблице распределения СТЬЮДЕНТА с учетом уровня значимости (α) и числа степеней свободы (k).

7. Оценка достоверности выборочных характеристик Если фактическое значение tx больше критического, то с определенной вероятностью мы можем утверждать, что полученные характеристики (параметры) достоверны и могут быть распространены на генеральную совокупность. Распространять эти характеристики можно с помощью различных приёмов: 1. СПОСОБ ПРЯМОГО ПЕРЕСЧЕТА применяют когда на основе выборки рассчитывают показатели генеральной совокупности, используя для этого выборочные средние или выборочные доли.

2. СПОСОБ КОЭФФИЦИЕНТОВ применяют для проверки и уточнения данных сплошного обследования (например, переписей). В этом случае, сопоставляя данные выборочного наблюдения со сплошным наблюдением исчисляют поправочный коэффициент – «процент недоучета», для внесения поправок в материалы сплошного наблюдения.

Конечной целью любого выборочного наблюдения является получение обобщающих характеристик изучаемой совокупности. При этом необходимо исходить из основного требования, предъявляемого к статистическому наблюдению: информация должна быть ДОСТОВЕРНОЙ, то есть максимально приближена к реальной действительности.