ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ 1. ВЕКТОРЫ НА ПЛОСКОСТИ



























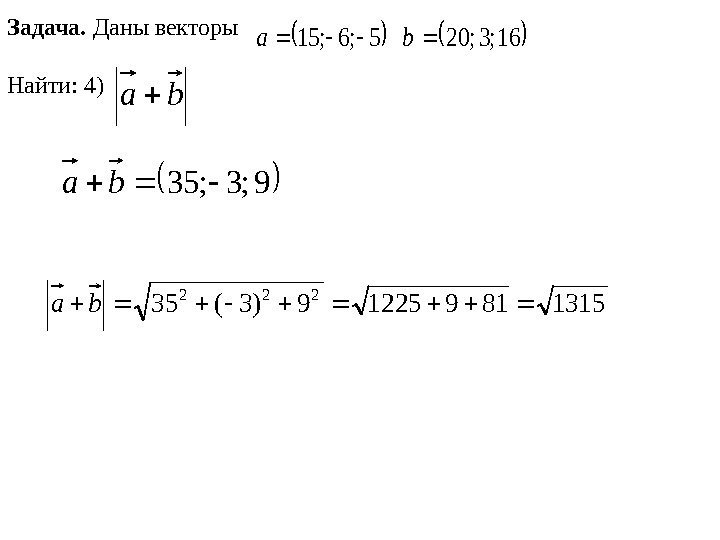

![Обозначения : ], [ или bacbac b c a Обозначения : ], [ или bacbac b c a](http://present5.com/presentforday2/20170121/vektor_algebradlya_zaochnikov_images/vektor_algebradlya_zaochnikov_32.jpg)






vektor_algebradlya_zaochnikov.ppt
- Размер: 623.0 Кб
- Автор: Елизавета Еремина
- Количество слайдов: 42
Описание презентации ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ 1. ВЕКТОРЫ НА ПЛОСКОСТИ по слайдам
 ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
 1. ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
1. ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
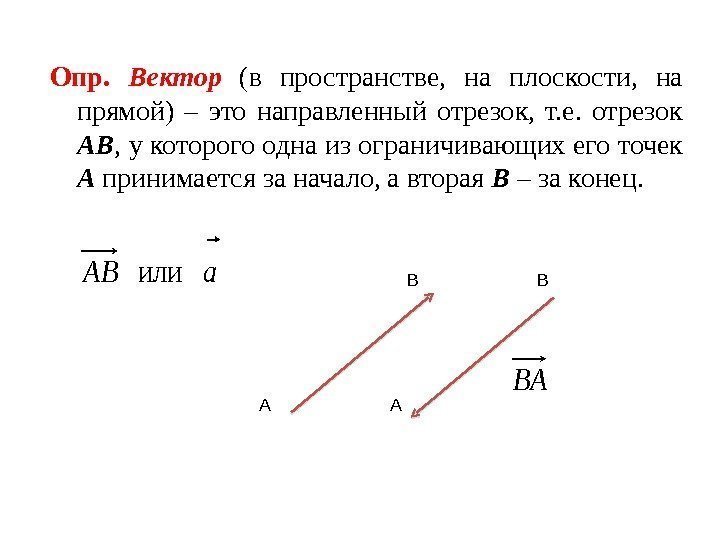
 Опр. Вектор (в пространстве, на плоскости, на прямой) – это направленный отрезок, т. е. отрезок AB , у которого одна из ограничивающих его точек A принимается за начало, а вторая B – за конец. a. AB или A B BА
Опр. Вектор (в пространстве, на плоскости, на прямой) – это направленный отрезок, т. е. отрезок AB , у которого одна из ограничивающих его точек A принимается за начало, а вторая B – за конец. a. AB или A B BА
 Опр. Ненулевые векторы называются равными : , если: 1) они лежат на одной прямой или на параллельных прямых; 2) имеют одинаковые длины ( ) и одинаково направлены. CDAB и CDAB A B C DВсе нулевые векторы считаются равными другу.
Опр. Ненулевые векторы называются равными : , если: 1) они лежат на одной прямой или на параллельных прямых; 2) имеют одинаковые длины ( ) и одинаково направлены. CDAB и CDAB A B C DВсе нулевые векторы считаются равными другу.
 Сложение векторов • Пусть — два произвольных вектора. Возьмем произвольную точку О и приложим вектор к этой точке, получим . • Затем отложим от точки А вектор , получим . Вектор называется суммой векторов . bа и ОAа b ОB АBb bа и OBABОА b а b О bа А B Правило параллелограмма b а с Правило треугольника bас
Сложение векторов • Пусть — два произвольных вектора. Возьмем произвольную точку О и приложим вектор к этой точке, получим . • Затем отложим от точки А вектор , получим . Вектор называется суммой векторов . bа и ОAа b ОB АBb bа и OBABОА b а b О bа А B Правило параллелограмма b а с Правило треугольника bас
 2. Разность векторов Опр. Разность векторов обозначается и определяется как сумма вектора и противоположного вектора . bа и bа а b b а а с bас О А Bb
2. Разность векторов Опр. Разность векторов обозначается и определяется как сумма вектора и противоположного вектора . bа и bа а b b а а с bас О А Bb
 3. Умножение вектора на число Опр. Произведение вектора на число называется вектор, длина которого равна числу и который имеет направление вектора , если 0, и противоположное направление ( ), если 0. Обозначается: . Если 0 или , то . а а а 0 а а а 3 а
3. Умножение вектора на число Опр. Произведение вектора на число называется вектор, длина которого равна числу и который имеет направление вектора , если 0, и противоположное направление ( ), если 0. Обозначается: . Если 0 или , то . а а а 0 а а а 3 а
 Опр. Два вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых. В противном случае, они называются неколлинеарными. bа и b а Коллинеарные векторы Неколлинеарные векторы Нулевой вектор коллинеарен всякому вектору и каждый вектор коллинеарен самому себе. Опр. Вектор называется коллинеарным прямой l , если этот вектор лежит либо на прямой l , либо прямой, параллельной l. а
Опр. Два вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых. В противном случае, они называются неколлинеарными. bа и b а Коллинеарные векторы Неколлинеарные векторы Нулевой вектор коллинеарен всякому вектору и каждый вектор коллинеарен самому себе. Опр. Вектор называется коллинеарным прямой l , если этот вектор лежит либо на прямой l , либо прямой, параллельной l. а
 Первый признак коллинеарности двух ненулевых векторов (следует из определения)числа. некоторые — и где , , abbaba
Первый признак коллинеарности двух ненулевых векторов (следует из определения)числа. некоторые — и где , , abbaba
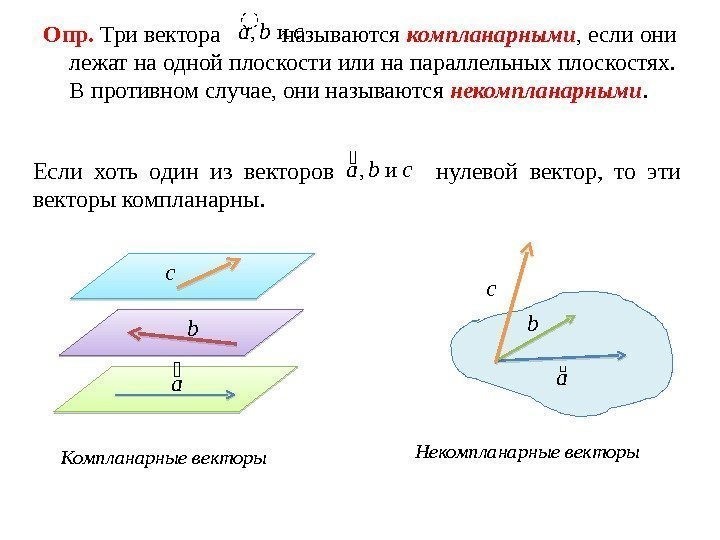
 Опр. Три вектора называются компланарными , если они лежат на одной плоскости или на параллельных плоскостях. В противном случае, они называются некомпланарными. сbа и , Если хоть один из векторов нулевой вектор, то эти векторы компланарны. сbа и , b а Компланарные векторы Некомпланарные векторы с с
Опр. Три вектора называются компланарными , если они лежат на одной плоскости или на параллельных плоскостях. В противном случае, они называются некомпланарными. сbа и , Если хоть один из векторов нулевой вектор, то эти векторы компланарны. сbа и , b а Компланарные векторы Некомпланарные векторы с с
 Множество всех свободных векторов на прямой будем обозначать R 1 , на плоскости — R 2 , в пространстве — R 3. Опр. Множества R 1 , R 2 , R 3 вместе с введёнными выше линейными операциями над векторами называются также векторными пространствами R 1 , R 2 , R 3.
Множество всех свободных векторов на прямой будем обозначать R 1 , на плоскости — R 2 , в пространстве — R 3. Опр. Множества R 1 , R 2 , R 3 вместе с введёнными выше линейными операциями над векторами называются также векторными пространствами R 1 , R 2 , R 3.
 Опр. 1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке. 2) Базисом на плоскости называются любые 2 неколлинеарных вектора, взятые в определенном порядке. 3) Базисом на прямой называется любой ненулевой вектор.
Опр. 1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке. 2) Базисом на плоскости называются любые 2 неколлинеарных вектора, взятые в определенном порядке. 3) Базисом на прямой называется любой ненулевой вектор.
 Опр. Если — базис в пространстве и , то числа , и — называются компонентами или координатами вектора в этом базисе. В связи с этим можно записать следующие свойства : 1) равные векторы имеют одинаковые координаты, 2) при умножении вектора на число его компоненты тоже умножаются на это число, 3) при сложении векторов складываются их соответствующие компоненты. 321 , , eee 321 eeea 321321)()(eeeeeea 332211 eeeb 333222111)()()(eee
Опр. Если — базис в пространстве и , то числа , и — называются компонентами или координатами вектора в этом базисе. В связи с этим можно записать следующие свойства : 1) равные векторы имеют одинаковые координаты, 2) при умножении вектора на число его компоненты тоже умножаются на это число, 3) при сложении векторов складываются их соответствующие компоненты. 321 , , eee 321 eeea 321321)()(eeeeeea 332211 eeeb 333222111)()()(eee
 Опр. Если — некоторая система векторов пространства R ( R 1 , R 2 или R 3 ) , тогда любой вектор вида называется линейной комбинацией векторов некоторые действительные числа, называемые коэффициентами линейной комбинации. Если какой-либо вектор представляется в виде линейной комбинации некоторых векторов, то говорят, что он разложен по этим векторам. naaa , . . . , , 21 пnгдеaaa, . . . , , 2121 nn aaa . . .
Опр. Если — некоторая система векторов пространства R ( R 1 , R 2 или R 3 ) , тогда любой вектор вида называется линейной комбинацией векторов некоторые действительные числа, называемые коэффициентами линейной комбинации. Если какой-либо вектор представляется в виде линейной комбинации некоторых векторов, то говорят, что он разложен по этим векторам. naaa , . . . , , 21 пnгдеaaa, . . . , , 2121 nn aaa . . .
 Опр. Векторы называются линейно зависимыми , если существует такая линейная комбинация , при не равных нулю одновременно i , т. е. . Если же только при i = 0 выполняется равенство , то векторы называются линейно независимыми. naa , . . . , 1 0. . . 2211 nnaaa 0. . . 22 2 2 1 n 0. . . 2211 nnaaa
Опр. Векторы называются линейно зависимыми , если существует такая линейная комбинация , при не равных нулю одновременно i , т. е. . Если же только при i = 0 выполняется равенство , то векторы называются линейно независимыми. naa , . . . , 1 0. . . 2211 nnaaa 0. . . 22 2 2 1 n 0. . . 2211 nnaaa
 Свойства 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы. 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима. 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов. 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны. 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны. 6. Любые 4 вектора линейно зависимы.
Свойства 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы. 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима. 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов. 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны. 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны. 6. Любые 4 вектора линейно зависимы.
 2. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
2. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
 • О – произвольная точка • единичные взаимно-перпендикулярные векторы плоскости (пространства) – орты • Oxy – прямоугольная система координат на плоскости • Oxyz – декартовая система координат в пространстве • x – абсцисса • y – ордината • z – аппликатаkjiji , , , y x. O i j y x O i j zk
• О – произвольная точка • единичные взаимно-перпендикулярные векторы плоскости (пространства) – орты • Oxy – прямоугольная система координат на плоскости • Oxyz – декартовая система координат в пространстве • x – абсцисса • y – ордината • z – аппликатаkjiji , , , y x. O i j y x O i j zk
 Вектор заданный на плоскости Oxy , может быть представлен в виде: a jyixa 11 где x 1 , y 1 – проекции вектора на соответствующие оси координат называются прямоугольными координатами вектора. y x. O A(x 1 , y 1 ) y 1 x 1 i j a Вектор с координатами x 1 и y 1 обозначается: и называется радиус-вектором точки А. OAa 11, yxa
Вектор заданный на плоскости Oxy , может быть представлен в виде: a jyixa 11 где x 1 , y 1 – проекции вектора на соответствующие оси координат называются прямоугольными координатами вектора. y x. O A(x 1 , y 1 ) y 1 x 1 i j a Вектор с координатами x 1 и y 1 обозначается: и называется радиус-вектором точки А. OAa 11, yxa
 Задача 1. Найти координаты вектора, если даны координаты его начальной и конечной точек. Решение. . , , , Но. Имеем ). , , ( и ), , ( Пусть 121212222111 zzyyxx. ABzyx. OA OAOBABzyx. А
Задача 1. Найти координаты вектора, если даны координаты его начальной и конечной точек. Решение. . , , , Но. Имеем ). , , ( и ), , ( Пусть 121212222111 zzyyxx. ABzyx. OA OAOBABzyx. А
 Условие коллинеарности двух векторов Векторы коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т. е. когда справедливо равенство 222111, , и, , zyxbzyxa 2 1 2 1 z z y y x x
Условие коллинеарности двух векторов Векторы коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т. е. когда справедливо равенство 222111, , и, , zyxbzyxa 2 1 2 1 z z y y x x
 Длина вектора в декартовых координатах: 2 1 2 1 zyxa 111, , zyxa Длина вектора в прямоугольных координатах : 11, yxa 2 1 yxa
Длина вектора в декартовых координатах: 2 1 2 1 zyxa 111, , zyxa Длина вектора в прямоугольных координатах : 11, yxa 2 1 yxa
 Линейные операции над векторами в координатной форме 111 212121 222111 ; ; Тогда , , и, , Если zyxa zzyyxxba zyxbzyxa
Линейные операции над векторами в координатной форме 111 212121 222111 ; ; Тогда , , и, , Если zyxa zzyyxxba zyxbzyxa
 Направление вектора определяется углами α , β , γ , образованными с осями координат Ox, Oy, Oz. Косинусы этих углов определяются по формулам: a x 1 cos ay 1 cos a z 1 cos
Направление вектора определяется углами α , β , γ , образованными с осями координат Ox, Oy, Oz. Косинусы этих углов определяются по формулам: a x 1 cos ay 1 cos a z 1 cos
 3. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
3. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
 Опр. Скалярным произведением двух векторов называется число , обозначаемое и равное ba и ba ), cos(bababa 212121 222111, , , Если zzyyxxba zyxbzyxa ba ba ba ), cos(
Опр. Скалярным произведением двух векторов называется число , обозначаемое и равное ba и ba ), cos(bababa 212121 222111, , , Если zzyyxxba zyxbzyxa ba ba ba ), cos(
 aba. Задача. Даны векторы Найти: 1) . 16 ; 3 ; 20 5; 6; 15 ba 21 ; 9 ; 5)5(16 ); 6(3 ; 1520 ab 8421)5(9)6(515 aba. Разность двух векторов: Скалярное произведение двух векторов:
aba. Задача. Даны векторы Найти: 1) . 16 ; 3 ; 20 5; 6; 15 ba 21 ; 9 ; 5)5(16 ); 6(3 ; 1520 ab 8421)5(9)6(515 aba. Разность двух векторов: Скалярное произведение двух векторов:
 a. Задача. Даны векторы Найти: 2) 16 ; 3 ; 20 5; 6; 15 ba 2862536225)5()6(15 222 a Длина вектора:
a. Задача. Даны векторы Найти: 2) 16 ; 3 ; 20 5; 6; 15 ba 2862536225)5()6(15 222 a Длина вектора:
 сa , cosbac 2 Задача. Даны векторы Найти: 3) если 16 ; 3 ; 20 5; 6; 15 ba 6 ; 9; 5016 ; 3 ; 205; 6; 1522 bac 2 3 2 3 2 1 2 1 313131 , cos zyxzyx zzyyxx ca ca сa 748462 774 2617286 3054750 6)9(50)5()6(15 6)5()9()6(5015 , cos 222222 сa
сa , cosbac 2 Задача. Даны векторы Найти: 3) если 16 ; 3 ; 20 5; 6; 15 ba 6 ; 9; 5016 ; 3 ; 205; 6; 1522 bac 2 3 2 3 2 1 2 1 313131 , cos zyxzyx zzyyxx ca ca сa 748462 774 2617286 3054750 6)9(50)5()6(15 6)5()9()6(5015 , cos 222222 сa
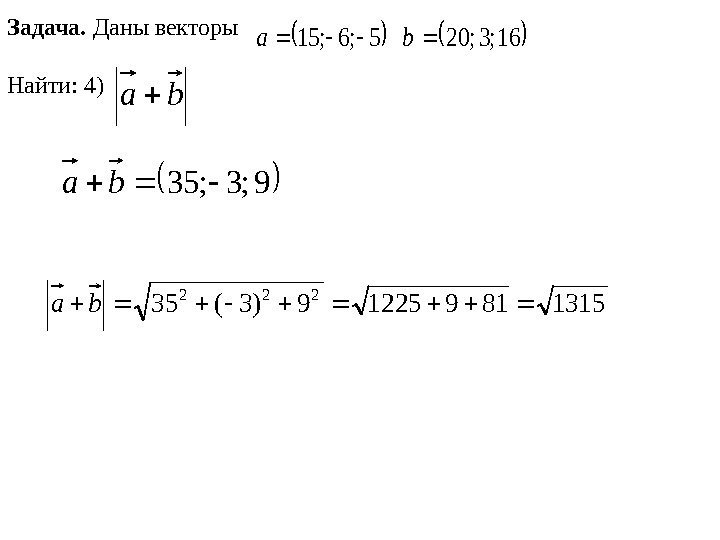 ba. Задача. Даны векторы Найти: 4) 16 ; 3 ; 20 5; 6; 15 ba 9 ; 3; 35 ba 131581912259)3(35 222 ba
ba. Задача. Даны векторы Найти: 4) 16 ; 3 ; 20 5; 6; 15 ba 9 ; 3; 35 ba 131581912259)3(35 222 ba
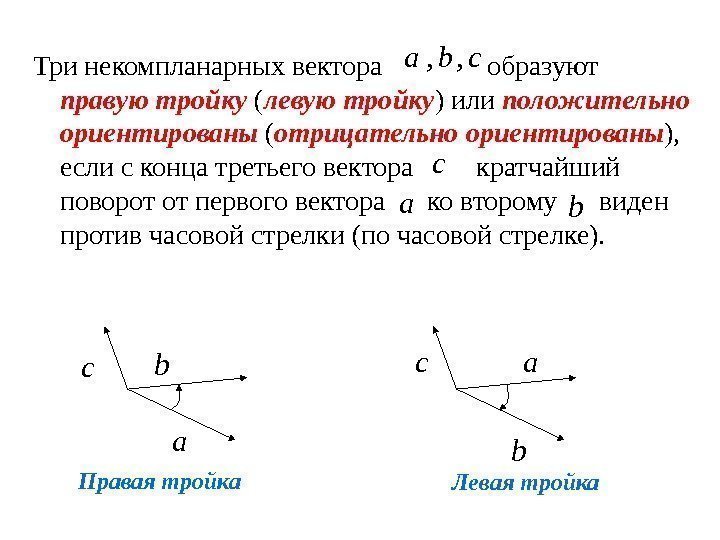
 Три некомпланарных вектора образуют правую тройку ( левую тройку ) или положительно ориентированы ( отрицательно ориентированы ), если с конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки (по часовой стрелке). b c cba , , a a a b b c c Правая тройка Левая тройка
Три некомпланарных вектора образуют правую тройку ( левую тройку ) или положительно ориентированы ( отрицательно ориентированы ), если с конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки (по часовой стрелке). b c cba , , a a a b b c c Правая тройка Левая тройка
 Векторное произведение векторов Опр. Векторным произведением двух векторов называется такой третий вектор , который удовлетворяет следующим трем условиям : 1) вектор ортогонален 2) 3) векторы образуют правую тройку. ba и с ), sin(babaс bcac и cba , ,
Векторное произведение векторов Опр. Векторным произведением двух векторов называется такой третий вектор , который удовлетворяет следующим трем условиям : 1) вектор ортогонален 2) 3) векторы образуют правую тройку. ba и с ), sin(babaс bcac и cba , ,
![Обозначения : ], [ или bacbac b c a Обозначения : ], [ или bacbac b c a](http://present5.com/presentforday2/20170121/vektor_algebradlya_zaochnikov_images/vektor_algebradlya_zaochnikov_32.jpg) Обозначения : ], [ или bacbac b c a
Обозначения : ], [ или bacbac b c a
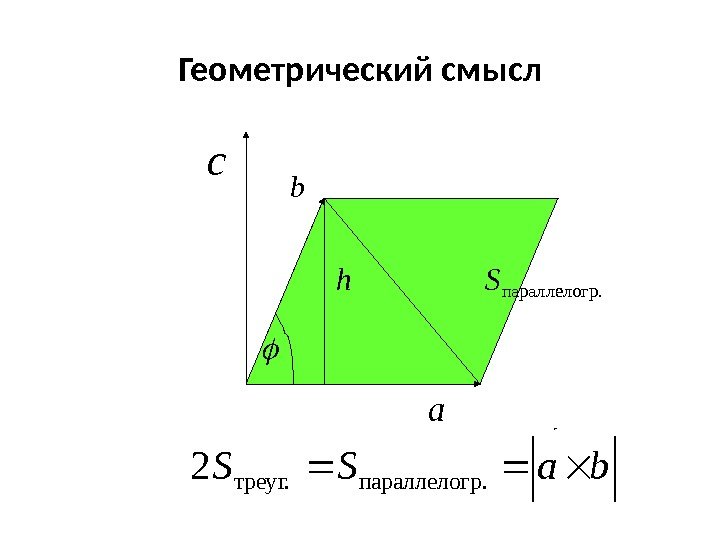
 Геометрический смыслba. SS р. параллелогтреуг. 2 с р. параллелог Sh b а
Геометрический смыслba. SS р. параллелогтреуг. 2 с р. параллелог Sh b а
 Свойства , 0||. 5 )(. 4 , )(. 3 , 0. 2 ), (. 1 baba векторовостиколлинеарн. Критерий bababa cabacba aa abba
Свойства , 0||. 5 )(. 4 , )(. 3 , 0. 2 ), (. 1 baba векторовостиколлинеарн. Критерий bababa cabacba aa abba
 6. Теорема (запись векторного произведения в координатах) Если делитель)псевдоопре( , , и , , 222 111 222111 zyx kji bac zyxbzyxa
6. Теорема (запись векторного произведения в координатах) Если делитель)псевдоопре( , , и , , 222 111 222111 zyx kji bac zyxbzyxa
 Смешанное произведение векторов Опр. Смешанным произведением трех векторов называется число , обозначаемое и определяемое следующим образом cba , , cba . c, b, a ), c, b, a( : яобозначени Другие c)ba(cba ×=
Смешанное произведение векторов Опр. Смешанным произведением трех векторов называется число , обозначаемое и определяемое следующим образом cba , , cba . c, b, a ), c, b, a( : яобозначени Другие c)ba(cba ×=
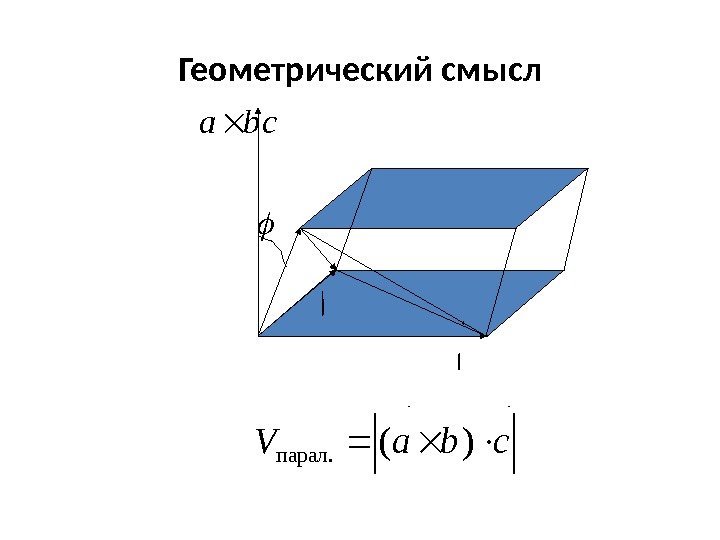
 Геометрический смыслa b cba. V )(парал. cba
Геометрический смыслa b cba. V )(парал. cba
 Свойстваcbdcbacbda ababbabaa cbacba )(. 4 0. 3 )(. 2 )()(.
Свойстваcbdcbacbda ababbabaa cbacba )(. 4 0. 3 )(. 2 )()(.
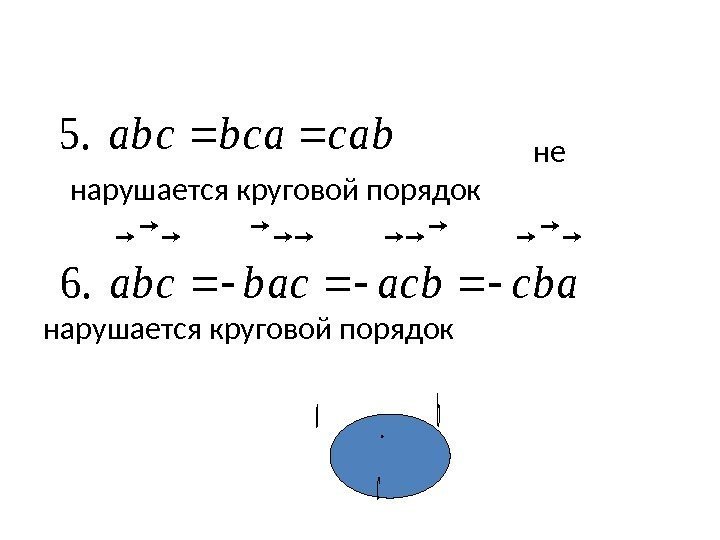
 не нарушается круговой порядокс ba abcbcacabcba bacacbcba . 6.
не нарушается круговой порядокс ba abcbcacabcba bacacbcba . 6.
 7. Теорема (запись смешанного произведения в координатах) Если . тогда , , , 333 222 111 zyx zyx cba zyxc zyxb zyxa
7. Теорема (запись смешанного произведения в координатах) Если . тогда , , , 333 222 111 zyx zyx cba zyxc zyxb zyxa
 8. Признак компланарности трех векторов (линейной зависимости трех векторов) Векторы компланарны (линейно зависимы) 0 0 333 222 111 zyx zyx cba , ,
8. Признак компланарности трех векторов (линейной зависимости трех векторов) Векторы компланарны (линейно зависимы) 0 0 333 222 111 zyx zyx cba , ,
