ОСНОВЫ ЛОГИКИ АЛГЕБРА в широком смысле этого

ОСНОВЫ ЛОГИКИ

АЛГЕБРА в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и так далее). Объектами алгебры логики являются высказывания.

Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт – истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.

Простые высказывания в алгебре логики обозначаются заглавными буквами А = { Аристотель – основоположник логики } В = { На яблонях растут бананы } Истинному высказыванию ставится в соответствие 1, ложному – 0. Таким образом, А = 1, В = 0.

Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности. содержание дальше

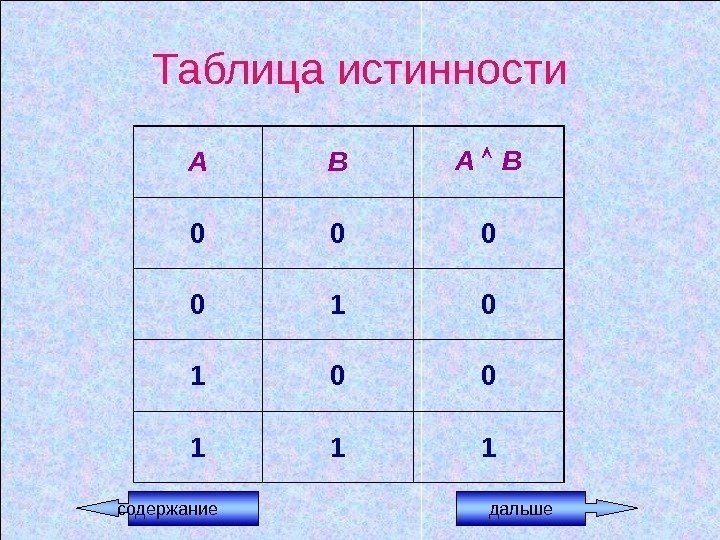
Логическая операция КОНЪЮНКЦИЯ (логическое умножение) • В естественном языке соответствует союзу и • В алгебре высказываний обозначается & • В языках программирования обозначается and

Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Пример. Даны высказывания. Определите истинность каждого из них. • А = { 10 делится на 2 и 5 не больше трех } • В = { 10 не делится на 2 и 5 больше трех } • С = { 10 делится на 2 и 5 больше трех } • D = { 10 не делится на 2 и 5 не больше трех } А = 1 0 = 0 В = 0 1 = 0 С = 1 1 = 1 D = 0 0 =

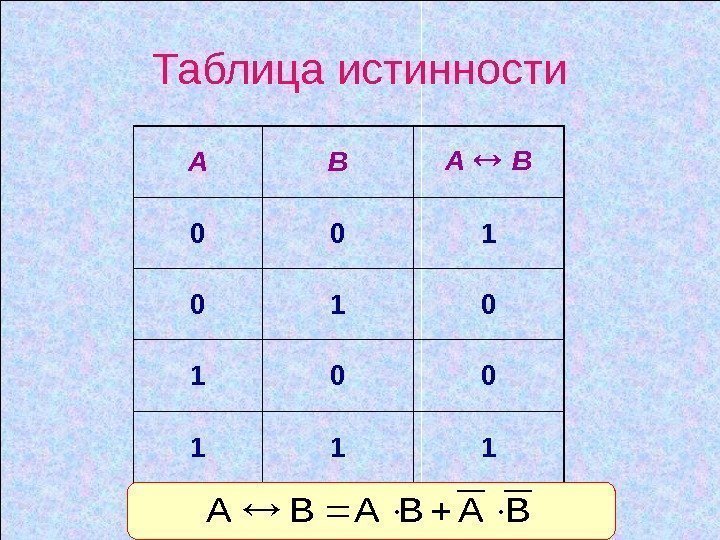
Таблица истинности А В А В 0 0 1 1 1 содержание дальше

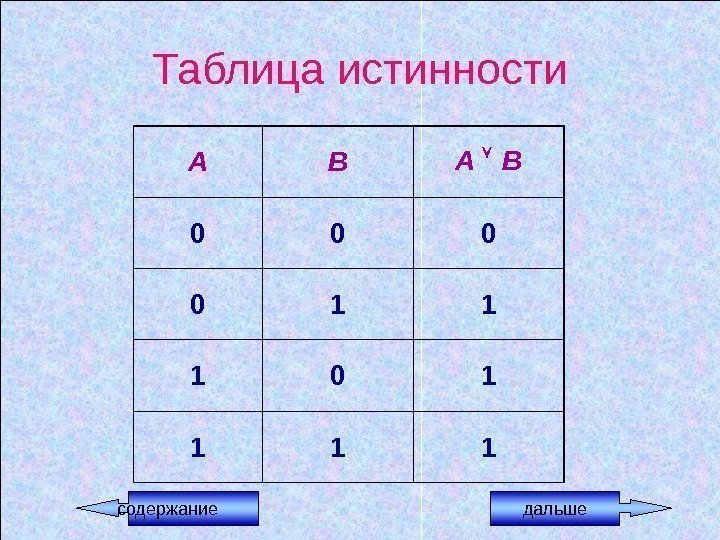
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение) • В естественном языке соответствует союзу или. • В алгебре высказываний обозначается • В языках программирования обозначается or.

Дизъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

Пример. Даны высказывания. Определите истинность каждого из них. • А = { 10 делится на 2 или 5 не больше трех } • В = { 10 не делится на 2 или 5 больше трех } • С = { 10 делится на 2 или 5 больше трех } • D = { 10 не делится на 2 или 5 не больше трех } A = 1 0 = 1 B = 0 1 = 1 C = 1 1 = 1 D = 0 0 =

Таблица истинности А В 0 0 1 1 1 0 1 1 содержание дальше

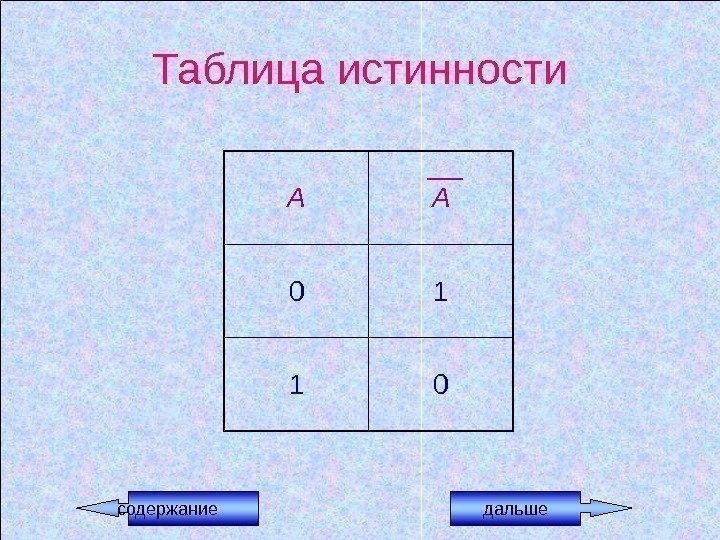
Логическая операция ОТРИЦАНИЕ (инверсия) • В естественном языке соответствует частице не. • В алгебре высказываний обозначается А, А • В языках программирования обозначается not

Отрицание – это логическая операция, которая каждому простому истинному высказыванию ставит в соответствие ложное высказывание.

Пример • А = { Луна – спутник Земли } • А = { Луна – не спутник Земли }

Таблица истинности А А 0 1 1 0 содержание дальше

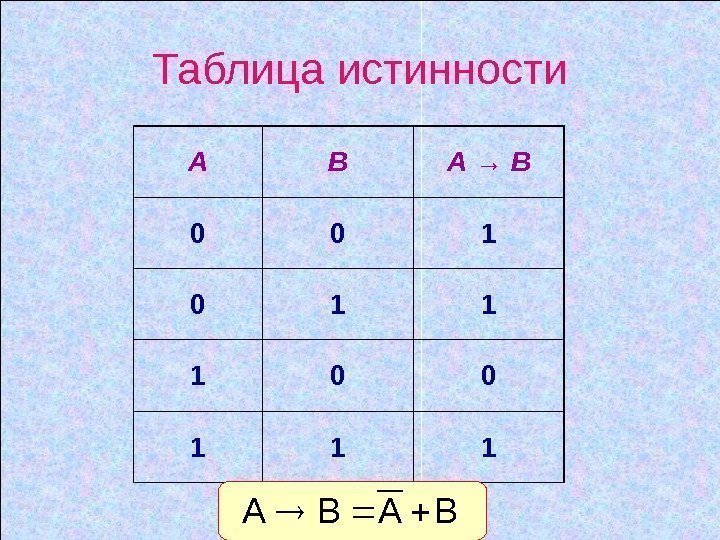
Логическая операция ИМПЛИКАЦИЯ (логическое следование) • В естественном языке соответствует обороту если …, то …. • В алгебре высказываний обозначается → • В языках программирования не используется

Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Пример. Даны высказывания. • А = { Данный четырехугольник — квадрат } • В = { Около данного четырехугольника можно описать окружность } Рассмотрим составное высказывание А → В , понимаемое как «если данный четырехугольник – квадрат, то около него можно описать окружность» . Есть три варианта, когда высказывание А → В истинно

1. А истинно и В истинно , т. е. если данный четырехугольник – квадрат, то около него можно описать окружность; 2. А ложно и В истинно , т. е. если данный четырехугольник не является квадратом, то около него можно описать окружность; 3. А ложно и В ложно , т. е. если данный четырехугольник не является квадратом, то около него нельзя описать окружность; Ложен только один вариант: А истинно и В ложно , т. е. если данный четырехугольник – квадрат, то около него нельзя описать окружность.

В обычной речи связка «если …, то» описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смеяться над бессмысленностью импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: «если президент США – демократ, то в Африке водятся жирафы» или «если арбуз ягода, то в бензоколонке есть бензин»

Таблица истинности А В А → В

Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность) • В естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае • В алгебре высказываний обозначается • В языках программирования не используется

Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или ложны.

Пример. Определить истинность высказываний. А = { 24 делится на 6 тогда и только тогда, когда 24 делится на 3 } А = 1 1 = 1 В = { 23 делится на 6 тогда и только тогда, когда 23 делится на 3 } В = 0 0 = 1 С = { 24 делится на 6 тогда и только тогда, когда 24 делится на 5 } С = 1 0 = 0 D = { 21 делится на 6 тогда и только тогда, когда 21 делится на 3 } D = 0 1 =

Таблица истинности А В

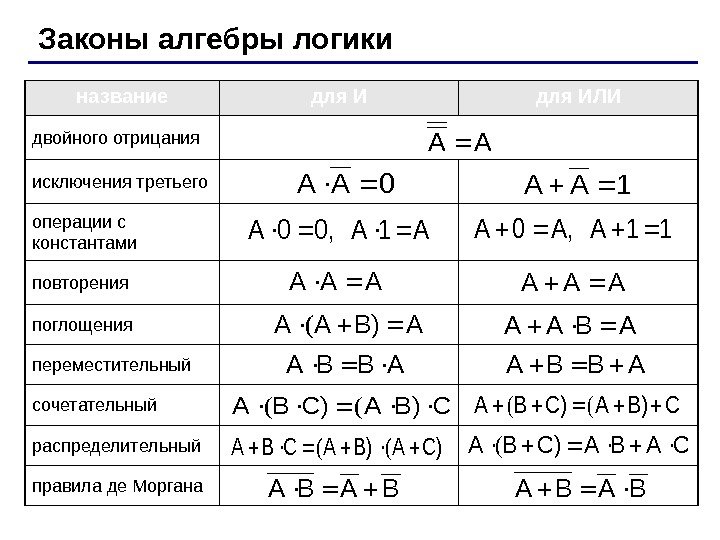
Законы алгебры логики название для ИЛИ двойного отрицания исключения третьего операции с константами повторения поглощения переместительный сочетательный распределительный правила де Моргана. AA 0 AA 1 AA A 1 A 0, 0 A 11 AA, 0 A AAA AB)AA ( ABAA ABBA CB)AC)BA(( C)AB)ACBA((CABAC)BA(

Разминка (упростите логические выражения) • 1 группа • 2 группа • 3 группа • 4 группа 1 группа 1)В 2) А 3)А v С, 2 группа 1)А & С 2) В 3)В , 3 группа 1)В 2) С & А 3)А & B , 4 группа 1)С 2) С 3) А v С,

1 ) Укажите, какое логическое выражение равносильно выражению ¬(A B) ¬C ? 1) ¬A B ¬C 2) ( ¬A ¬B) ¬C 3) ( ¬A ¬B) C 4) ¬A ¬B ¬CЗадания группы А 8 Преобразование логических выражений. Формулы де Моргана. 1) ¬A B ¬C 2) (¬A ¬B) ¬C 3) (¬A ¬B) C 4) ¬A ¬B ¬

Решение 1) Применим закон де Моргана. Получим : CBACBA)()( CBA)( 3) Таким образом, правильный ответ – 2 2) Сравним результат с предлагаемыми ответами 1) ¬A B ¬C 2) (¬A ¬B) ¬C 3) (¬A ¬B) C 4) ¬A ¬B ¬

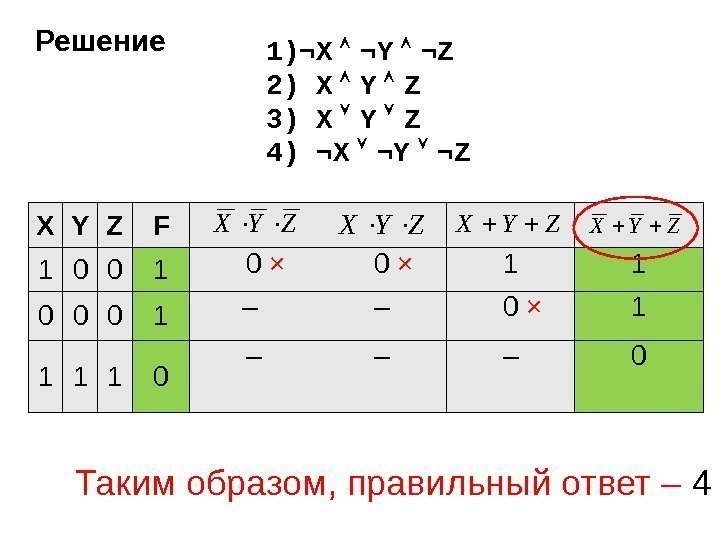
2 ) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F : Какое выражение соответствует F ? 1) ¬X ¬Y ¬Z 2) X Y Z 3) X Y Z 4) ¬X ¬Y ¬Z X Y Z F 1 0 0 0 1 1 0 Задания группы А 9 Построение таблиц истинности логических выражений. 1) ¬X ¬Y ¬Z 2) X Y Z 3) X Y Z 4) ¬X ¬Y ¬Z

Решение X Y Z F 1 0 0 1 0 × 1 1 0 0 0 1 – – 0 × 1 1 0 – – – 0 ZYXZYX Таким образом, правильный ответ – 41) ¬X ¬Y ¬Z 2) X Y Z 3) X Y Z 4) ¬X ¬Y ¬Z

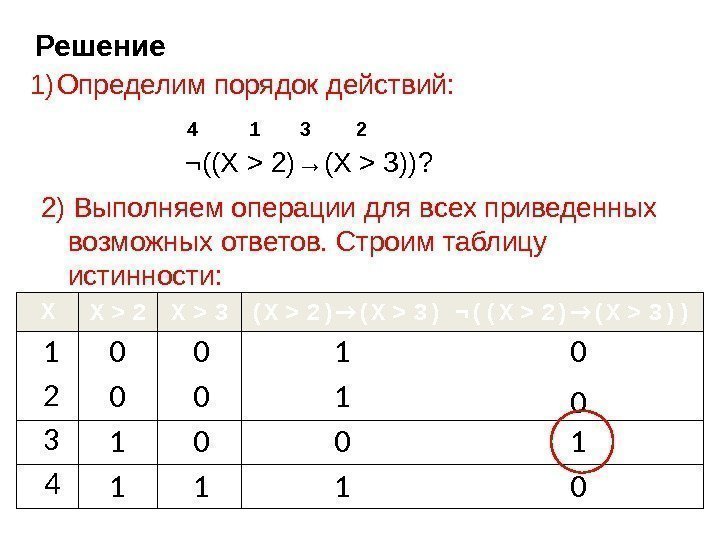
Задания группы А 7 4) Для какого из указанных значений X истинно высказывание ¬((X >> 2)2) →→ (X(X >> 3))3)) ? ? 1) 1 2) 2 3) 3 4) 4 Основные понятия математической логики.

Решение 1) Определим порядок действий: X X > 2 X > 3 (X > 2) → (X > 3) ¬((X > 2) → (X > 3)) 1 2 3 42) Выполняем операции для всех приведенных возможных ответов. Строим таблицу истинности: ¬((X > 2)→(X > 3))?

5) Для какого имени истинно высказывание ¬(ПЕРВАЯ БУКВА СОГЛАСНАЯ ВТОРАЯ БУКВА СОГЛАСНАЯ) ПОСЛЕДНЯЯ БУКВА ГЛАСНАЯ ? ? 1) РОМАН 3) АНДРЕЙ 4) КРИСТИНА 2) ЮНОНАЗадания группы А 7 Основные понятия математической логики.

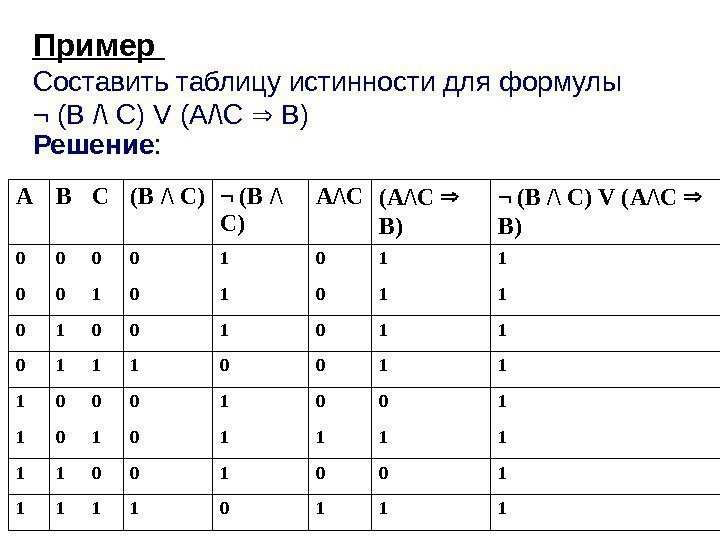
Пример Составит ь таблицу истинности для формулы ¬ ( B /\ C ) V ( A /\ C B ) Решение : A B C ( B /\ C ) ¬ ( B /\ C) A /\ C ( A /\ C B ) ¬ ( B /\ C ) V ( A /\ C B )

Логическое выражение называется тождественно-истинным , если оно принимает значения 1 на всех наборах входящих в него простых высказываний. Тождественно-истинные формулы называют тавтологиями. . Логическое выражение называется тождественно-ложным , если оно принимает значения 0 на всех наборах входящих в него простых высказываний.

Решение логических задач

Как решать логические задачи ? Три способа решения логических задач: 1. Средствами алгебры логики 2. Табличный 3. С помощью рассуждений

Решение задач средствами алгебры логики Схема решения: 1. Изучается условие задачи 2. Вводится система обозначений 3. Составляется логическая формула 4. Определяется значения логической формулы

Задача «История Нового года» Три друга обсуждали историю Нового года, при этом каждый сказал следующее: • Празднование Нового года с 1 января установили во Франции в 45 году до Рождества Христова (Юлием Цезарем) • Празднование Нового года с 1 января установили римляне в 1659 году указом Карла IX • Празднование Нового года с 1 января установили во 2 веке и не французы Оказавшийся рядом знаток истории сказал, что каждый из них прав только в одном из двух высказанных предложений. Где и в какое время было установлено празднование Нового года с 1 января?

Задача « История Нового года» Обозначения: Ф – французы Р – римляне К – Карл IX в 1659 Ц – Цезарь В – 2 век

Задача « История Нового года» Логическая формула: (Ф & не. Ц + не. Ф & Ц) & (Р & не. К + не. Р & К) & & (не. В & не. Ф +Ф & В)= упростим логическую формулу воспользуемся распределительным законом

Задача « История Нового года» Логическая формула: (Ф & не. Ц + не. Ф & Ц) & (Р & не. К + не. Р & К) & & (не. В & не. Ф +Ф & В)= =((Ф & не. Ц+не. Ф & Ц) & Р & не. К+(Ф & не. Ц+не. Ф & Ц) & & не. Р & К) & (не. В & не. Ф+Ф & В)= = (Ф & не. Ц & Р & не. К+не. Ф & Ц & Р & не. К+Ф & не. Ц & & не. Р & К+не. Ф & Ц & не. Р & К) & (не. В & не. Ф+Ф & В)= Т. к. Ф & Р=0, Ц & К=0, то получаем следующую формулу

Задача « История Нового года» Логическая формула: =(не. Ф & Ц & Р & не. К+Ф & не. Ц & не. Р & К) & & (не. В & не. Ф+Ф & В)= = (не. Ф & Ц & Р & не. К+Ф & не. Ц & не. Р & К) & не. В & не. Ф+ (не. Ф & Ц & Р & не. К+Ф & не. Ц & не. Р & К) & Ф & В= Т. к. Ф & не. Ф=0, не. Ф & не. Ф=не. Ф, Ф & Ф=Ф то получаем =не. Ф & Ц & Р & не. К & не. В+Ф & не. Ц & не. Р & К & В =

Задача « История Нового года» Логическая формула: =(не. Ф & Ц & Р & не. К+Ф & не. Ц & не. Р & К) & & (не. В & не. Ф+Ф & В)= = (не. Ф & Ц & Р & не. К+Ф & не. Ц & не. Р & К) & не. В & не. Ф+ (не. Ф & Ц & Р & не. К+Ф & не. Ц & не. Р & К) & Ф & В= Т. к. Ф & не. Ф=0, не. Ф & не. Ф=не. Ф, Ф & Ф=Ф то получаем =не. Ф & Ц & Р & не. К & не. В+Ф & не. Ц & не. Р & К & В, т. к. К & В=0, то получаем следующую формулу:

Задача « История Нового года» Логическая формула: =Ц & Р & не. К & не. В & не. Ф формула принимает значение истинно только при Ц=1, Р=1, К=0, В=0, Ф=0 Ответ: Празднование Нового года с 1 января установили римляне в 45 году до Рождества Христова (благодаря введению нового календаря Юлием Цезарем )

« 8 Марта – день борьбы за права женщин» Три друга, интересующиеся историей, обсуждали историю возникновения праздника 8 Марта как дня борьбы за права женщин, и каждый сказал следующее: • 8 Марта как день борьбы за права женщин возник в 1857 году в России • 8 Марта как день борьбы за права женщин возник в 1900 году в США • 8 Марта как день борьбы за права женщин возник в 1920 году и не в России Оказавшийся рядом учитель истории сказал, что каждый из них прав только в одном из двух высказанных предположений. Где и в каком году 8 Марта стали считать днём борьбы за права женщин?

« 8 Марта – день борьбы за права женщин» А — возник в России В – возник в 1857 г. С – возник в США ¬ В – возник в 1900 г. D — возник в 1920 г. (A v. B )&(¬ В v. C)&(Dv¬A)=1 ((A&¬B)v(A&C)v(B&¬B)v (B&C))&(Dv¬A)=1 (A&¬B&D)v(A&¬B&¬A)v(A&C&D)v(A&C&¬A)v(B&C&D)v(B&C&¬A)=1 (A&¬B&D)v 0 v(A&C&D)v 0 v(B&C&D)v(B&C&¬A)=1 A&¬B&D=0 A&C&D=0 B&C&¬A=1 Ответ: возник в 1857 году в США Справка: Возник этот праздник как день борьбы за права женщин 8 марта 1857 года в Нью-Йорке, где работницы швейных и обувных фабрик вышли на демонстрацию с требованиями об улучшении своих условий работы и предоставлении им прав наравне с мужчинами.

Решение задач табличным способом Схема решения: Результаты рассуждений фиксируются с помощью специально составленных таблиц

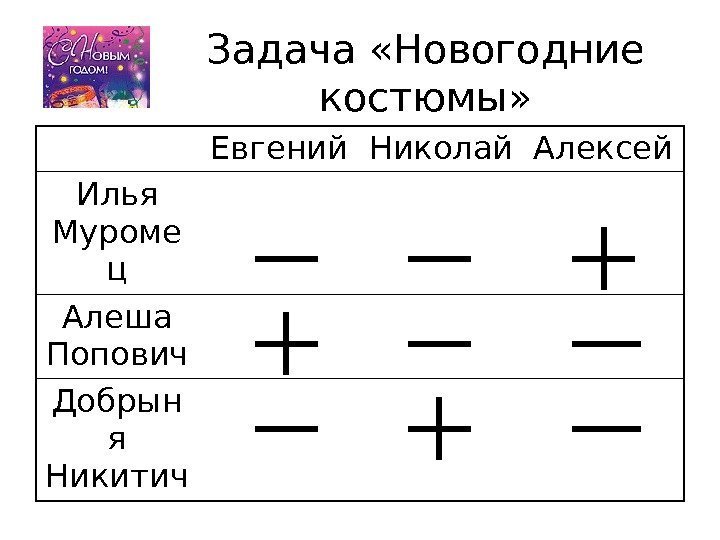
Задача «Новогодние костюмы» На новогодний праздник три друга – Евгений, Николай, Алексей , выбрали себе костюмы трех богатырей: Ильи Муромца, Алеши Попович, Добрыни Никитича. Известно, что: • Евгений – самый высокий • Выбравший костюм Добрыни Никитича меньше ростом, чем выбравший костюм Ильи Муромца • Алексею не подошел костюм Добрыни Никитича • Ни у одного из друзей имена не совпадает с именем богатырей, выбранных костюмов Какой костюм выбрал каждый из друзей?

Задача «Новогодние костюмы» Евгений Николай Алексей Илья Муроме ц Алеша Попович Добрын я Никитич

«Кто кому подарил подарок? » На весенний праздник три друга – Сергей, Николай, Алексей подарили подарки следующим девушкам: Татьяне, Марине, Алёне. Известно, что: • Подаривший подарок Татьяне меньше ростом, чем подаривший подарок Марине. • Сергей – самый высокий. • Алексей не дарил подарка Татьяне. • Ни у одного из друзей первая буква имени не совпадает с первой буквой имени девушки, которой они сделали подарки. Кто кому подарил подарок?

«Кто кому подарил подарок? » Ответ: Сергей – Алёне, Николай – Татьяне, Алексей – Марине. Справка: Уже в Древнем Риме существовал женский день. В этот день матроны (свободно рожденные женщины), состоящие в браке, получали от своих мужей подарки, были окружены любовью и вниманием. Рабыни тоже получали подарки. Кроме того, хозяйка дома позволяла невольницам в этот день отдыхать. На весенний праздник три друга – Сергей, Николай, Алексей подарили подарки следующим девушкам: Татьяне, Марине, Алёне. Известно, что: Подаривший подарок Татьяне меньше ростом, чем подаривший подарок Марине. Сергей – самый высокий. Алексей не дарил подарка Татьяне. Ни у одного из друзей первая буква имени не совпадает с первой буквой имени девушки, которой они сделали подарки. Кто кому подарил подарок?

Решение логических задач с помощью рассуждений Этим способом обычно решают несложные логические задачи

Задача «Новогодний подарок» Известно, что на одной двери надпись истинна, а на другой ложна. Если надпись на первой двери — «за этой дверью есть подарок», а на второй двери — «подарок за обоими дверьми», то: 1) подарок за обоими дверьми; 2) подарок только за второй дверью; 3) подарка нет ни за одной дверью; 4) подарок только за первой дверью; 5) определенно место подарка установить нельзя. Выберите вариант ответа

Ответ: Подарок только за первой дверью. Задача «Новогодний подарок»

«Где, когда и кто? » Три пожилых матроны, сидя вечером на лавочке, завели разговор о празднике 8 марта. Вот, что они сказали: • В 1910 году на Международной конференции женщин в Копенгагене Клара Цеткин выступила с предложением о праздновании Международного женского дня 8 марта, которое прозвучало, как призыв ко всем женщинам мира включиться в борьбу за равноправие. • В 1910 году на Международной конференции женщин в Москве или Копенгагене не Александра Коллонтай выступила с предложением о праздновании Международного женского дня 8 марта, которое прозвучало, как призыв ко всем женщинам мира включиться в борьбу за равноправие. • В 1911 году на Международной конференции женщин в Москве и не Клара Цеткин выступила с предложением о праздновании Международного женского дня 8 марта, которое прозвучало, как призыв ко всем женщинам мира включиться в борьбу за равноправие. Оказалось, что две из трёх женщин были совершенно правы, а предположение третьей полностью неверное. Где, когда и кто выступил на международной конференции женщин?

«Где, когда и кто? » Предположим, что высказывание первой дамы верное, т. е. в 1910 году на Международной конференции женщин в Копенгагене Клара Цеткин выступила с предложением о праздновании Международного женского дня 8 марта. Тогда, из рассуждений второй дамы, мы можем сделать вывод, что она тоже полностью права. А третья высказала полностью ложное предположение. В варианте с истинностью третьего высказывания мы получаем два ложных, а такого быть не может по условию задачи. Значит наше предположение верно. Ответ: в 1910 году в Копенгагене Клара Цеткин.

«Где лежат подарки? » В канун праздника 8 Марта девушки 10 класса зашли в свой кабинет. Там, на столе, стояли две коробки. На коробках наклеены надписи: на первой – «Подарки в обеих коробках» , а на второй – «В этой коробке есть подарки» . Где лежат подарки, если одна надпись истинна, а другая ложна.

«Где лежат подарки? » Во второй коробке , т. к. если предположить обратное, то мы получает два истинных высказывания, а у нас по условию одно высказывание ложно, а другое — истинно.

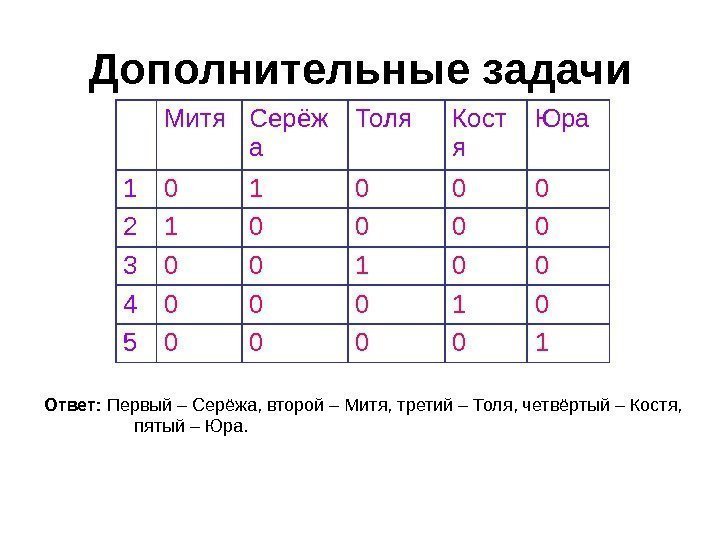
Дополнительные задачи 1. Митя, Сережа, Толя, Костя и Юра решили первыми поздравить своих девочек, а поэтому пораньше прийти в школу. Но оказалось, что Митя пришел позже Сережи, Толя раньше Кости, Митя раньше Толи, Юра позже Кости. В какой последовательности ребята пришли в школу?

Дополнительные задачи Митя Серёж а Толя Кост я Юра 1 0 0 0 2 1 0 0 3 0 0 1 0 0 4 0 0 0 1 0 5 0 0 1 Ответ: Первый – Серёжа, второй – Митя, третий – Толя, четвёртый – Костя, пятый – Юра.

Дополнительные задачи 2. Татьяна, Светлана, Людмила и Ирина участвовали в конкурсе «А, ну-ка, девушки!» и заняли четыре первых места. Когда их спросили о распределении мест, они ответили так: а) Татьяна — первая, Светлана — вторая; б) Татьяна — вторая, Ирина — третья; в) Людмила — вторая, Ирина — четвертая. Известно, что в каждом ответе только одно утверждение верно. Как распределились места?

Дополнительные задачи А -Татьяна первая В — Светлана вторая С — Ирина третья ¬ А — Татьяна вторая ¬ С — Ирина четвертая D — Людмила вторая (A v. B )&(¬ А v. C)&(Dv¬ С )=1 ((A&¬ А )v(A&C)v(B&¬ А )v(B&C))&(Dv¬ С )=1 (A&C&D)v(A&C&¬ С )v( В & ¬ А &D)v( В & ¬ А &¬ С) v(B&C&D)v(B&C&¬ С )=1 (A&C&D)v 0 v(B&¬A&D)v(B& ¬ А & ¬ С )v(B&C&D)v 0=1 A&C&D=1 B&¬A&D=0 B&C&¬A=0 B&C&D=0 Ответ: Татьяна – первая, Людмила – вторая, Ирина – третья, Светлана – четвертая.