Основы квантовой механики Экспериментальные основы КМ Основа

Основы квантовой механики

Экспериментальные основы КМ Основа любого варианта механики — ИЗМЕРЕНИЕ Наблюдаемая Невоспроизводимость результатов измерений А 9 А 7 А 6 А 5 А 4 А 3 А 2 А 1 Время

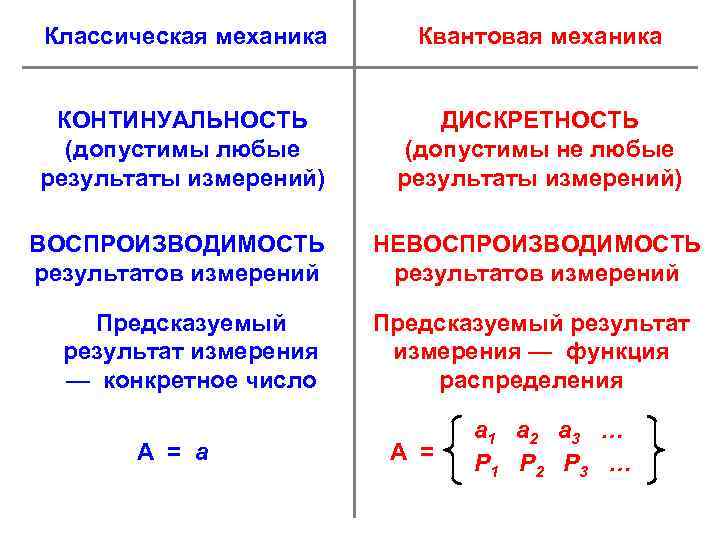Классическая механика Квантовая механика КОНТИНУАЛЬНОСТЬ (допустимы любые результаты измерений) ДИСКРЕТНОСТЬ (допустимы не любые результаты измерений) ВОСПРОИЗВОДИМОСТЬ результатов измерений НЕВОСПРОИЗВОДИМОСТЬ результатов измерений Предсказуемый результат измерения — конкретное число А = а Предсказуемый результат измерения — функция распределения А = а 1 а 2 а 3 … Р 1 Р 2 Р 3 …

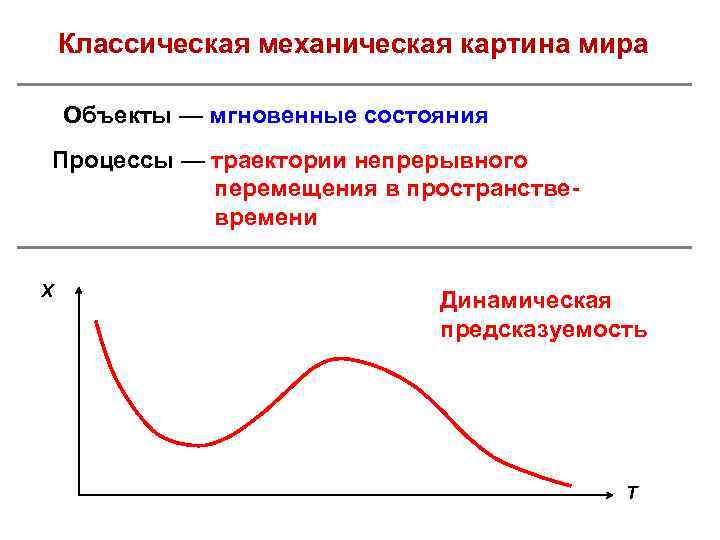Классическая механическая картина мира Объекты — мгновенные состояния Процессы — траектории непрерывного перемещения в пространствевремени Х Динамическая предсказуемость T

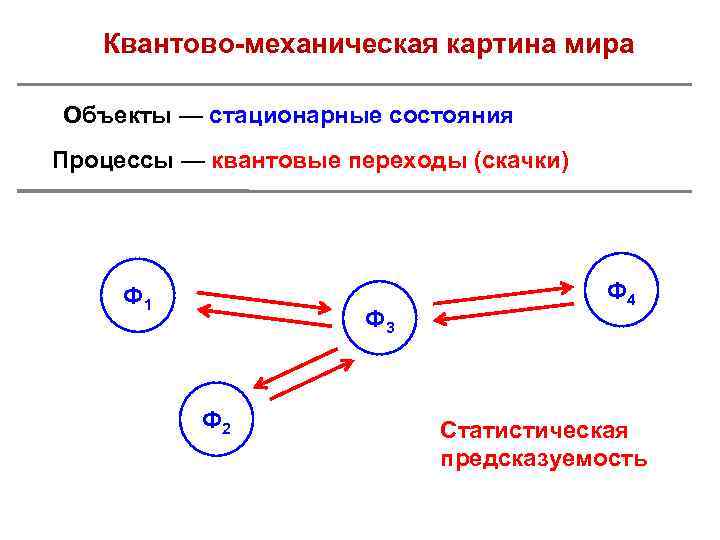Квантово-механическая картина мира Объекты — стационарные состояния Процессы — квантовые переходы (скачки) Ф 1 Ф 3 Ф 2 Ф 4 Статистическая предсказуемость

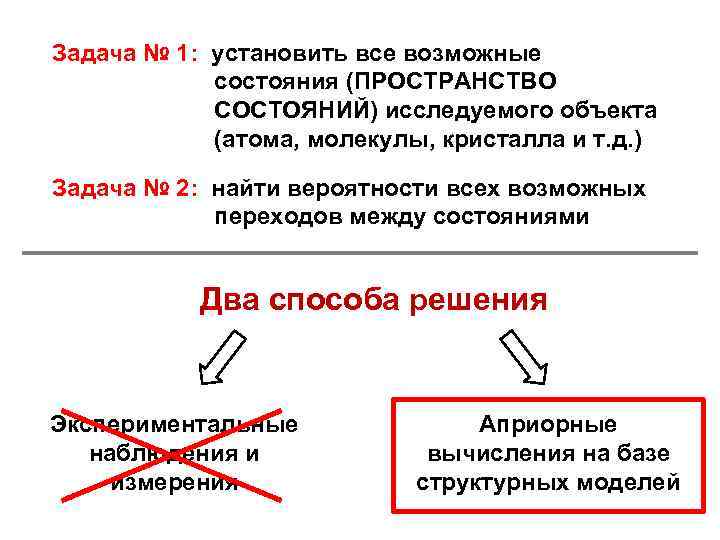Задача № 1: установить все возможные состояния (ПРОСТРАНСТВО СОСТОЯНИЙ) исследуемого объекта (атома, молекулы, кристалла и т. д. ) Задача № 2: найти вероятности всех возможных переходов между состояниями Два способа решения Экспериментальные наблюдения и измерения Априорные вычисления на базе структурных моделей

09. 2015

Основные ПОНЯТИЯ квантовой механики

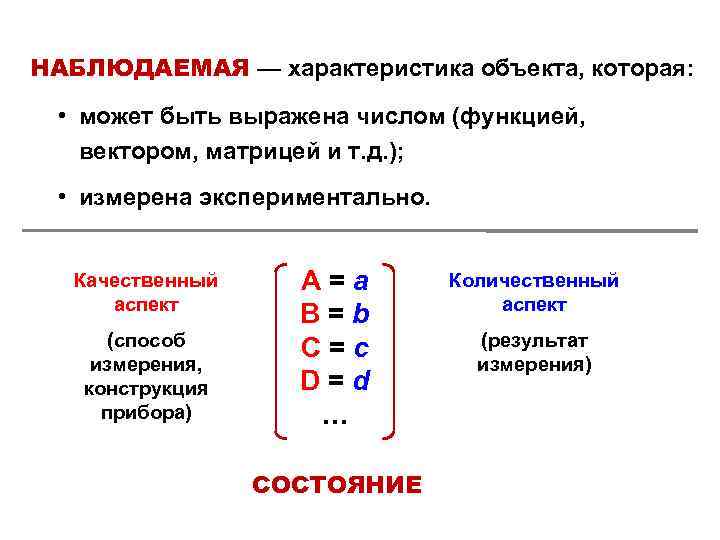НАБЛЮДАЕМАЯ — характеристика объекта, которая: • может быть выражена числом (функцией, вектором, матрицей и т. д. ); • измерена экспериментально. Качественный аспект (способ измерения, конструкция прибора) А=а B=b C=c D=d … СОСТОЯНИЕ Количественный аспект (результат измерения)

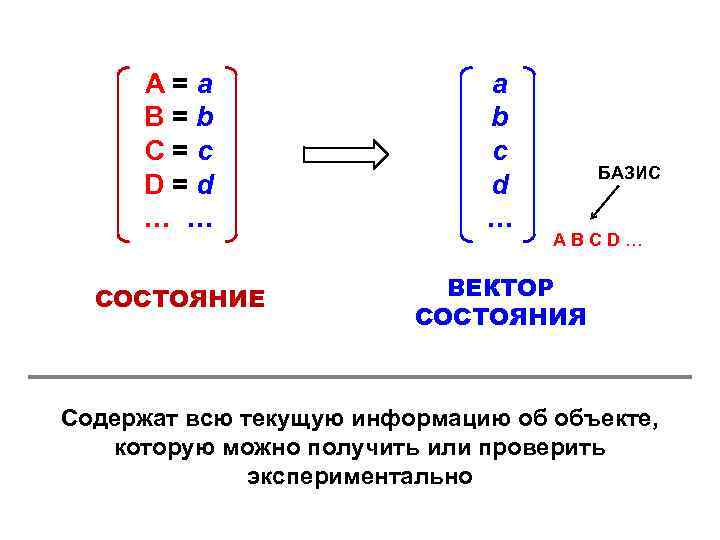А=а B=b C=c D=d … … а b c d … СОСТОЯНИЕ ВЕКТОР СОСТОЯНИЯ БАЗИС ABCD… Содержат всю текущую информацию об объекте, которую можно получить или проверить экспериментально

Φ 1 = а 1 b 1 c 1 d 1 … Φ 1 + Φ 2 = а 1 + а 2 b 1 + b 2 с1 + c 2 d 1 + d 2 … = а 3 b 3 c 3 d 3 … Принцип суперпозиции а 2 b 2 c 2 d 2 … = Φ 3

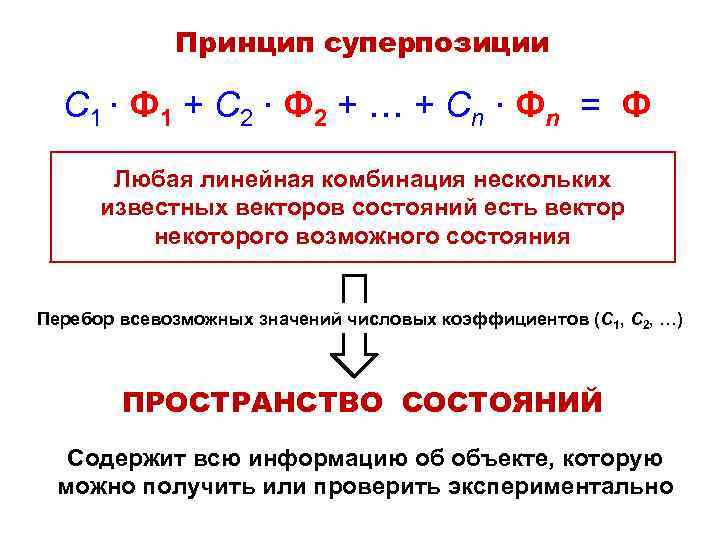Принцип суперпозиции С 1 ∙ Ф 1 + С 2 ∙ Ф 2 + … + Cn ∙ Ф n = Ф Любая линейная комбинация нескольких известных векторов состояний есть вектор некоторого возможного состояния Перебор всевозможных значений числовых коэффициентов (С 1, С 2, …) ПРОСТРАНСТВО СОСТОЯНИЙ Содержит всю информацию об объекте, которую можно получить или проверить экспериментально

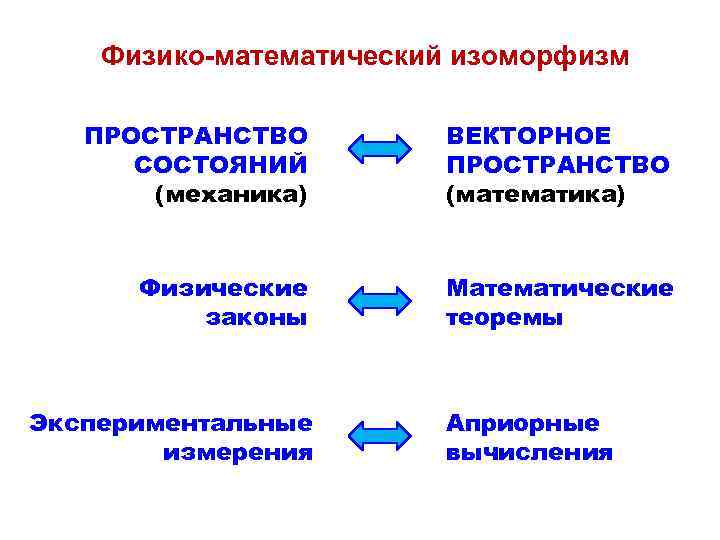Физико-математический изоморфизм ПРОСТРАНСТВО СОСТОЯНИЙ (механика) ВЕКТОРНОЕ ПРОСТРАНСТВО (математика) Физические законы Математические теоремы Экспериментальные измерения Априорные вычисления

Физические РЕЗУЛЬТАТЫ Математические СТРУКТУРНЫЕ МОДЕЛИ 1. Векторные пространства 2. Группы 3. Топологические графы 4. Скалярные и векторные поля …………………. .

Абстрактные векторные пространства

1. Множество ВЕКТОРОВ V = { a, b, c, d, … } 2. Операция «сложения» (коммутативная): a+b = b+a = c 3. Вспомогательная операция «умножения на число» : a = a = d Правило: результат обеих операций — вектор, принадлежащий тому же множеству V , что и исходные векторы

Условия ассоциативности (a + b) = a + b ( + ) a = a + а Линейные комбинации a + b + c +… = d СИНТЕЗ (из нескольких известных векторов можно получать все новые и новые векторы) a + b + c +… d АНАЛИЗ (любой «плохой» вектор можно заменить ЛК «хороших» векторов) d a + b + c +…

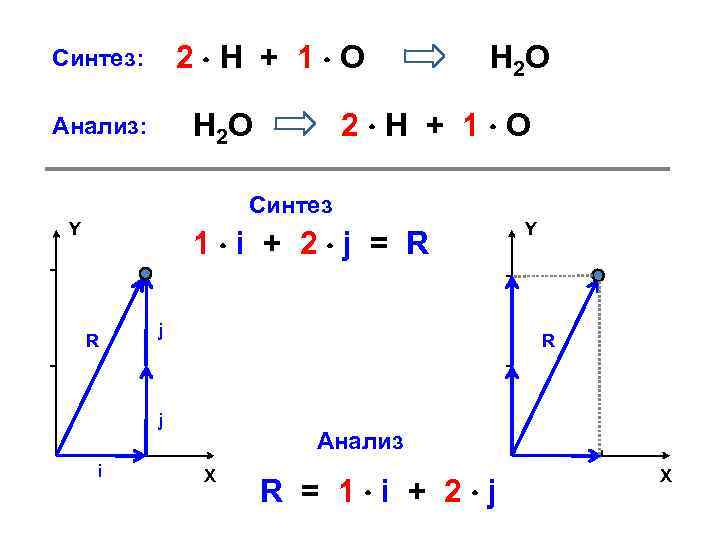2 Н + 1 О Синтез: 2 Н + 1 О Н 2 О Анализ: Н 2 О Синтез Y 1 i + 2 j = R R j i Y Анализ X R = 1 i + 2 j X

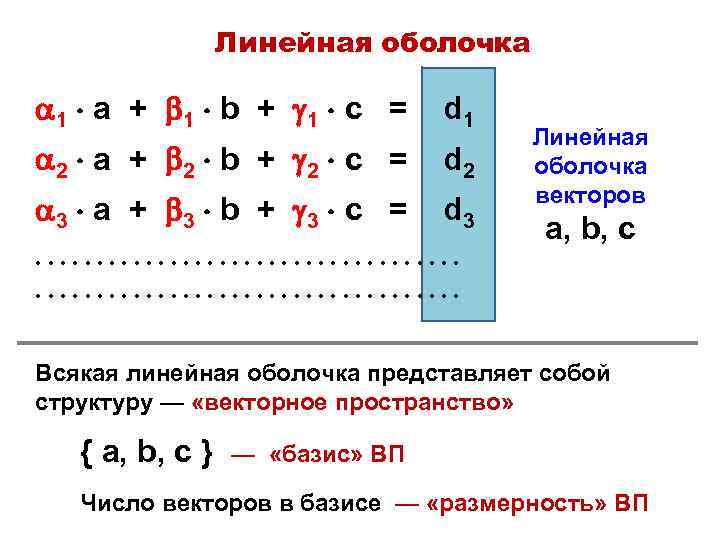Линейная оболочка 1 a + 1 b + 1 c = d 1 2 a + 2 b + 2 c = d 2 3 a + 3 b + 3 c = d 3 Линейная оболочка векторов a, b, c • • • • • • • • • • • • • • • • • • Всякая линейная оболочка представляет собой структуру — «векторное пространство» { a, b, c } — «базис» ВП Число векторов в базисе — «размерность» ВП

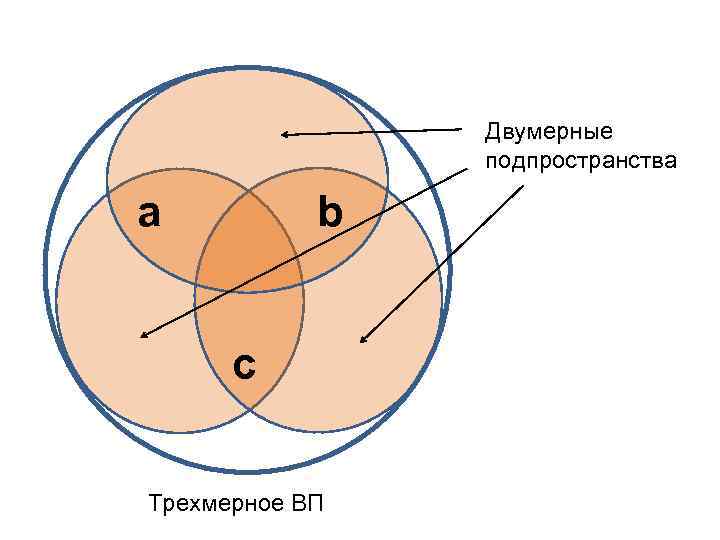Двумерные подпространства a b c Трехмерное ВП

В любом ВП существует не один базис, а бесконечно много эквивалентных между собой базисов (несмотря на то, что в такие наборы входят различные векторы, их линейные оболочки в точности совпадают и составляют одно и то же ВП). Число векторов в любом базисном наборе одинаково Все ВП одинаковой размерности изоморфны другу, т. е. для каждой размерности существует только одно ВП (если абстрагироваться от физического смысла векторов)

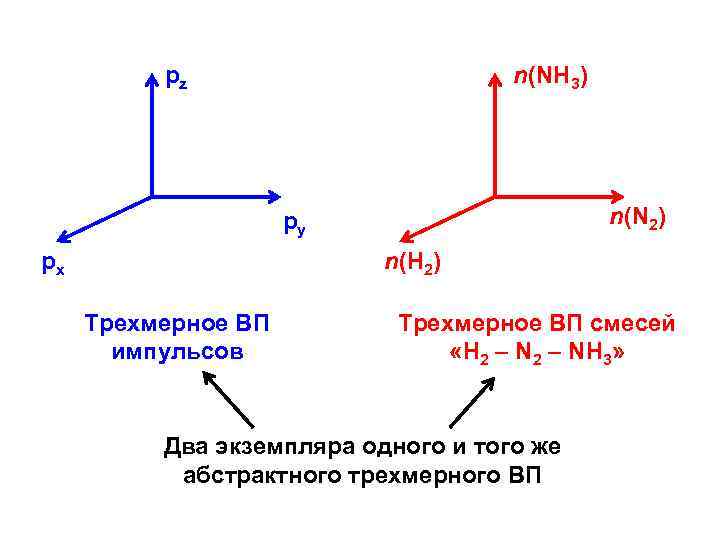pz n(NH 3) n(N 2) py px n(H 2) Трехмерное ВП импульсов Трехмерное ВП смесей «H 2 – NH 3» Два экземпляра одного и того же абстрактного трехмерного ВП

Координатное представление векторов ВП → базис { е 1, е 2, …, еn } X = x 1 e 1 + x 2 e 2 + … + xn e n Y = y 1 e 1 + y 2 e 2 + … + yn e n Z = z 1 e 1 + z 2 e 2 + … + zn en • • • • • • • • • • X = ( x 1, x 2, … , x n ) Y = ( y 1, y 2, … , y n ) Z = ( z 1, z 2, … , zn ) Координатные представления векторов X, Y, Z относительно базиса { е 1, е 2, …, еn }

1. Всякому вектору Х соответствует упорядоченный набор чисел-координат ( х1, х2, …, хn ) 2. Всякий упорядоченный набор чисел ( х1, х2, …, хn ) можно рассматривать как вектор Х X = ( x 1, x 2, … , x n ) Вектор-строка (ковариантный вектор) Х Х транспонирование X = x 1 x 2 … xn Вектор-столбец (контравариантный вектор)

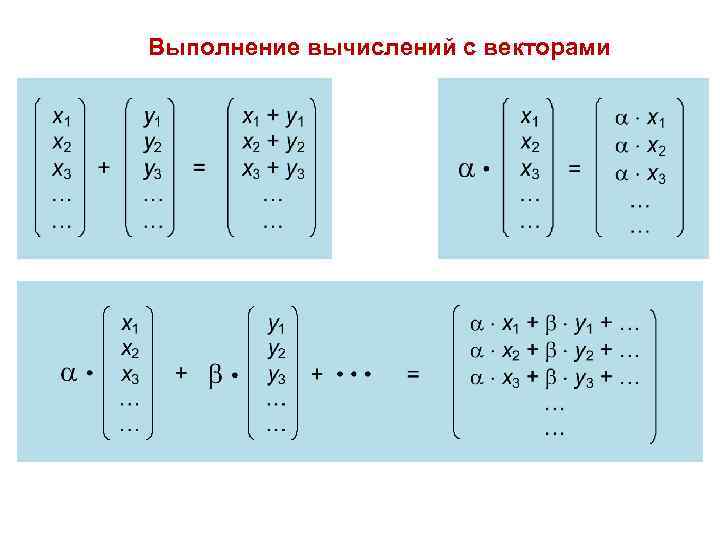Выполнение вычислений с векторами

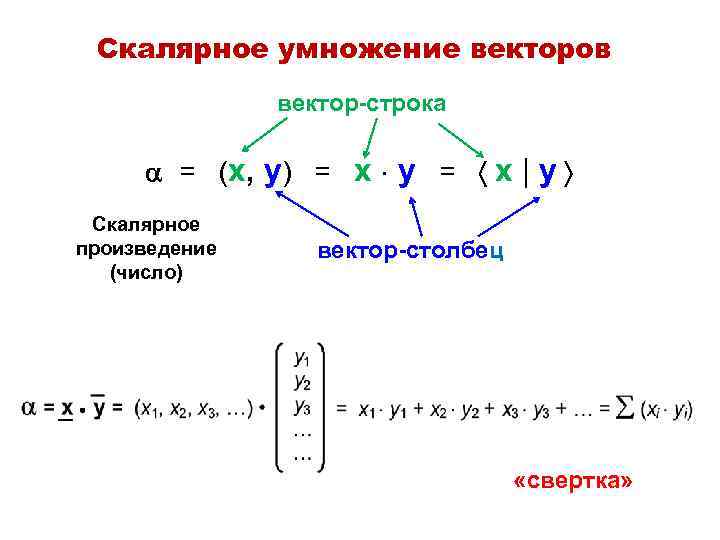Скалярное умножение векторов вектор-строка = (x, y) = x y = x | y Скалярное произведение (число) вектор-столбец «свертка»

Скалярный квадрат Х Х = (xi xi) = (xi)2 = |X| 2 | X | — модуль или норма вектора Х Нормировка векторов X = ( x 1, x 2, … , xn ) |X| ≠ 1 Обычный (ненормированный) вектор ~ X = x 1 x 2 |X| Нормированный вектор • • • xn |X| ~ |X| = 1

Луч — совокупность векторов, различающихся только длиной (модулем, нормой). {k X} где k — любое число, а X — нормированный вектор Луч — любое одномерное подпространство (координатная ось), а нормированный вектор — его базис (генератор) Векторное пространство — прямая сумма независимых лучей ВП = X Y Z • • •

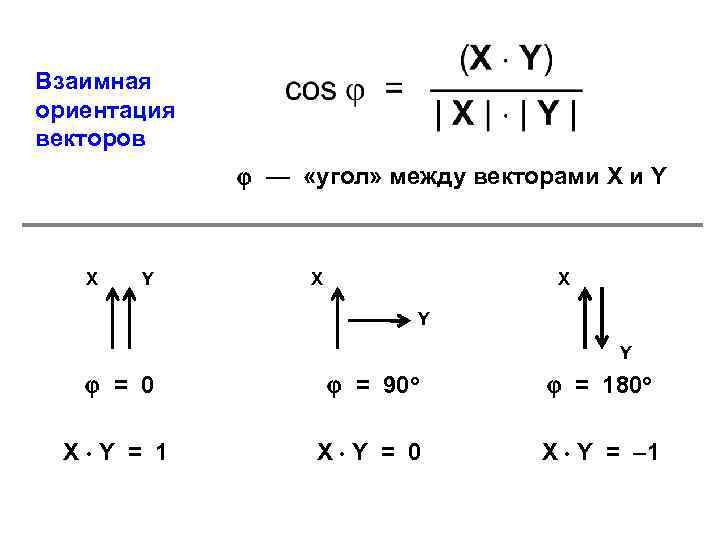Взаимная ориентация векторов — «угол» между векторами X и Y X X Y Y = 0 = 90 o = 180 o X Y = 1 X Y = 0 X Y = – 1

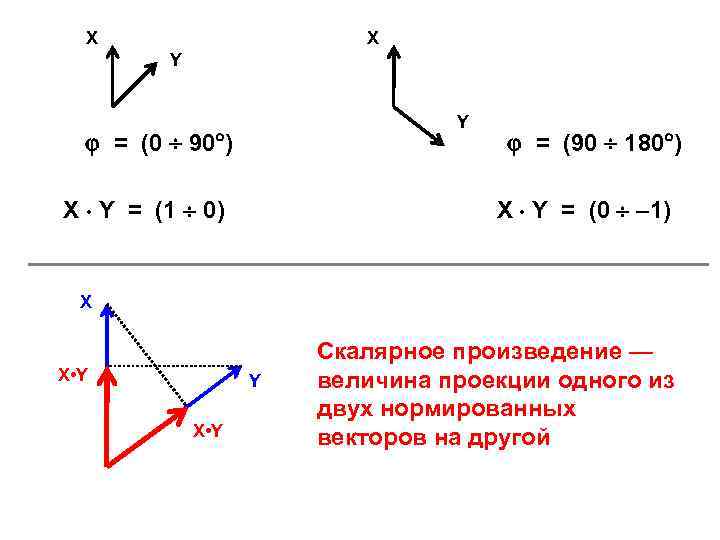X X Y Y = (0 90 ) X Y = (1 0) = (90 180 ) X Y = (0 – 1) X X • Y Y X • Y Скалярное произведение — величина проекции одного из двух нормированных векторов на другой

Комплексные векторы Z = ( z 1, z 2, … , zn ) Комплексные числа Z | = ( z 1, z 2, … , zn ) бра-вектор Z| = |Z + Z (z 1)* (z 2)* … (zn)* |Z = Z| Эрмитово-сопряженные векторы = |Z кет-вектор +

23. 09. 2015

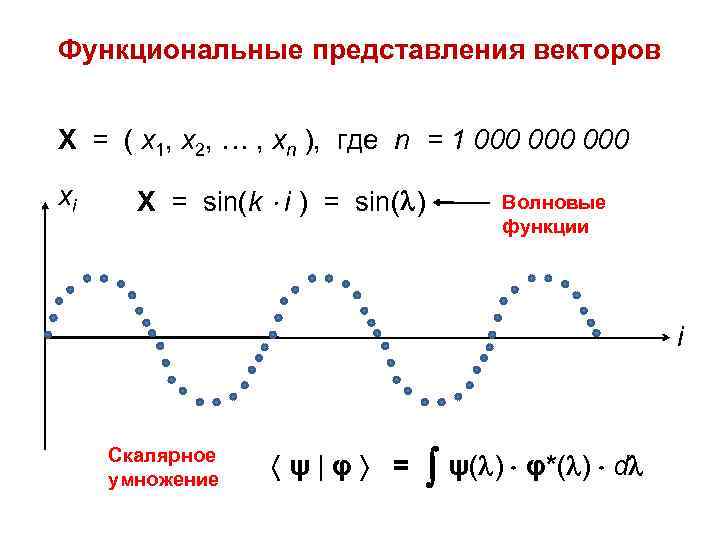Функциональные представления векторов X = ( x 1, x 2, … , xn ), где n = 1 000 000 xi X = sin(k i ) = sin( ) Волновые функции i Скалярное умножение ψ|φ = ψ( ) φ*( ) d

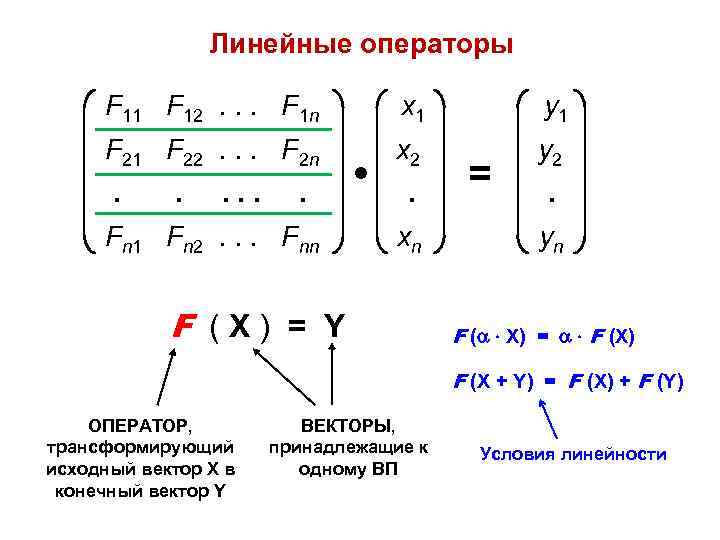Линейные операторы F 11 F 12. . . F 1 n x 1 y 1 F 22. . . F 2 n x 2 y 2 . . . Fn 1 Fn 2. . . Fnn • . xn F (X) = Y = . yn F ( X) = F (X) F (X + Y) = F (X) + F (Y) ОПЕРАТОР, трансформирующий исходный вектор X в конечный вектор Y ВЕКТОРЫ, принадлежащие к одному ВП Условия линейности

Преобразование векторов-строк F 11 F 12. . . F 1 n ( x 1 x 2 … xn ) • F 21 F 22. . . F 2 n. . . = ( y 1 y 2 … yn ) Fn 1 Fn 2. . . Fnn F (X) = Y «столбец столбец» (X)F = Y «строка строка»

1. Любая квадратная матрица может выступать в роли оператора 2. Любой оператор может быть изображен в виде квадратной матрицы Единичный оператор 1 0 0 x 0 1 0 • y 0 0 1 z Оператор растяжения 2 0 0 x 0 2 0 • y 0 0 2 z Оператор проектирования на ось Z 0 0 0 x 0 0 0 • y 0 0 1 z = x y z = 2 x 2 y 2 z = 0 0 z

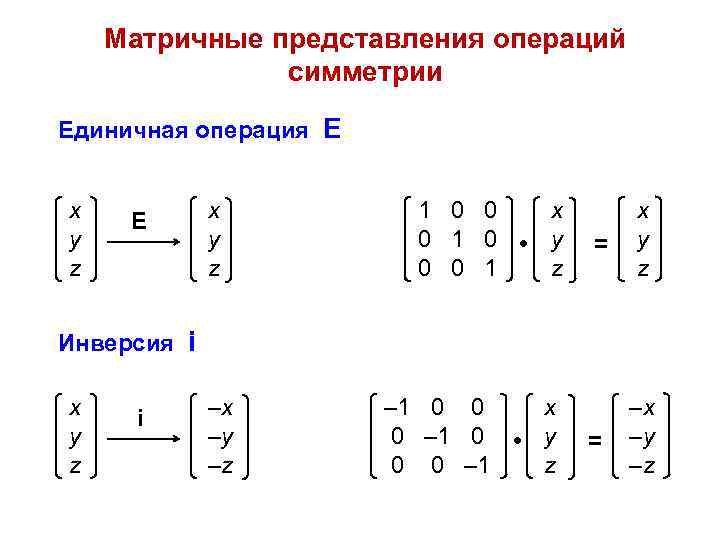Матричные представления операций симметрии Единичная операция E x y z Е x y z 1 0 0 x 0 1 0 • y 0 0 1 z = x y z = –x –y –z Инверсия i x y z i –x –y –z – 1 0 0 x 0 – 1 0 • y 0 0 – 1 z

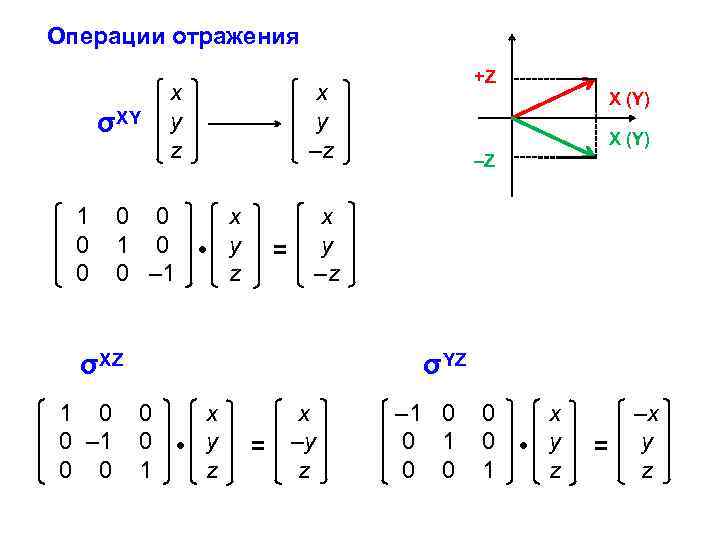Операции отражения x y z x y –z 0 0 x 1 0 • y 0 – 1 z x y –z σXY 1 0 0 = σXZ 1 0 0 – 1 0 0 +Z X (Y) –Z σYZ 0 x 0 • y 1 z = x –y z – 1 0 0 0 x 0 • y 1 z = –x y z

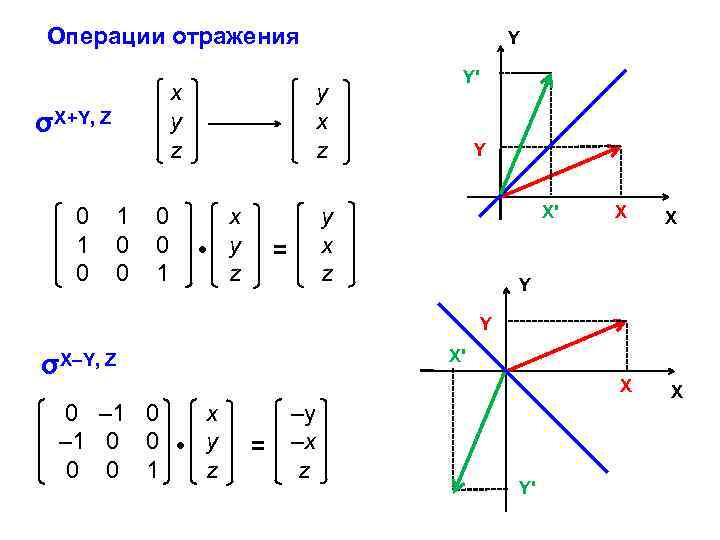Операции отражения x y z σX+Y, Z 0 1 0 0 1 Y y x z x • y z Y' Y X' y x z = X X Y Y X' σX–Y, Z 0 – 1 0 x – 1 0 0 • y 0 0 1 z X = –y –x z Y' X

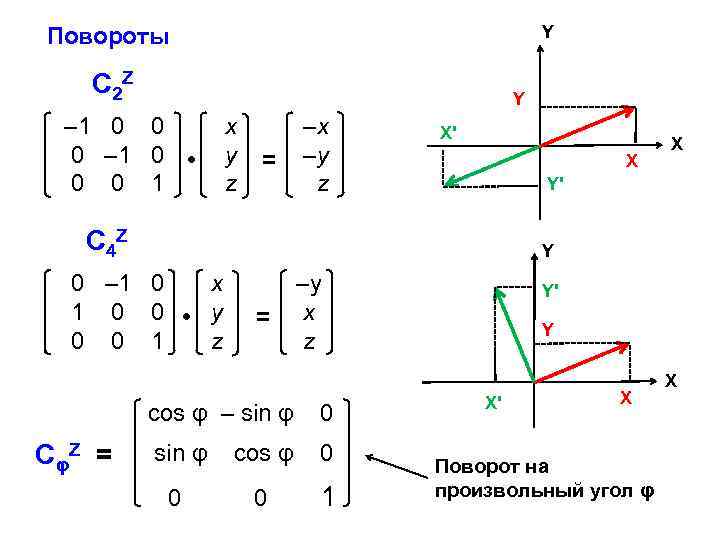Y Повороты С 2 Z Y – 1 0 0 0 – 1 0 • 0 0 1 x y z = –x –y z X' X Y' С 4 Z Y 0 – 1 0 x 1 0 0 • y 0 0 1 z = –y x z cos φ – sin φ Сφ Z = X 0 sin φ cos φ 0 0 0 1 Y' Y X' X Поворот на произвольный угол φ X

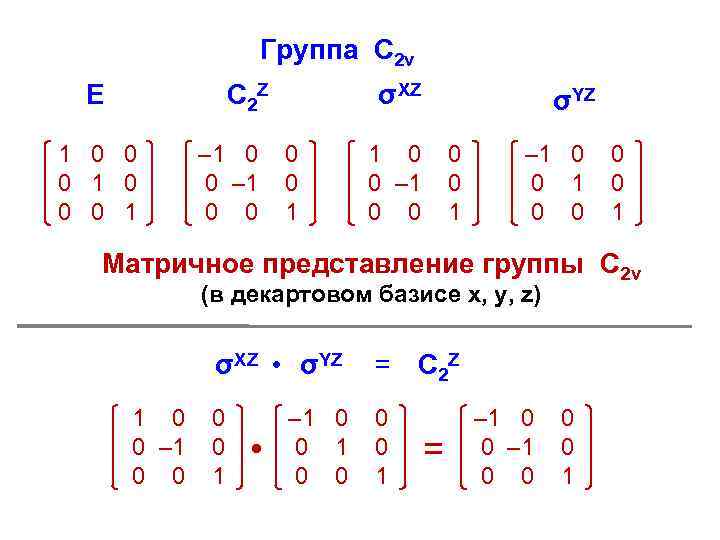Группа С 2 v E C 2 Z 1 0 0 0 1 – 1 0 0 σXZ 0 0 1 σYZ 1 0 0 – 1 0 0 1 – 1 0 0 0 0 1 Матричное представление группы С 2 v (в декартовом базисе x, y, z) σXZ • σYZ 1 0 0 – 1 0 0 = C 2 Z 0 0 1 • – 1 0 0 = – 1 0 0 0 0 1

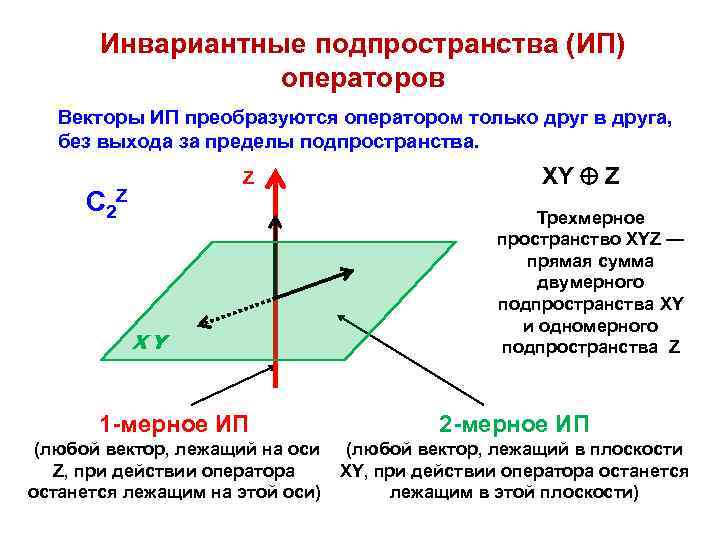Инвариантные подпространства (ИП) операторов Векторы ИП преобразуются оператором только друг в друга, без выхода за пределы подпространства. Z C 2 Z ХY XY Z Трехмерное пространство XYZ — прямая сумма двумерного подпространства XY и одномерного подпространства Z 1 -мерное ИП 2 -мерное ИП (любой вектор, лежащий на оси Z, при действии оператора останется лежащим на этой оси) (любой вектор, лежащий в плоскости XY, при действии оператора останется лежащим в этой плоскости)

Трехмерное пространство XYZ — прямая сумма двумерного подпространства XY и одномерного подпространства Z XY Z Это означает, что любой вектор трехмерного пространства XYZ может быть представлен в виде векторной суммы двух его проекций — на ось Z и плоскость XY R = RZ + RXY

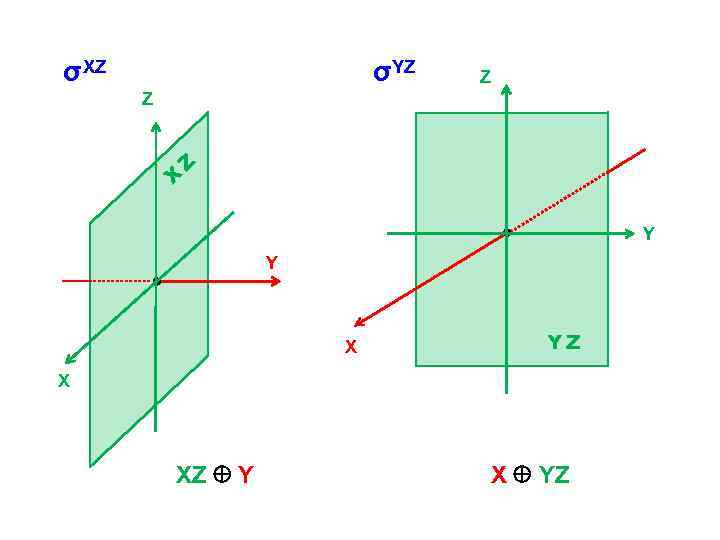σXZ σYZ Z Z X Z Y Y X YZ X XZ Y X YZ

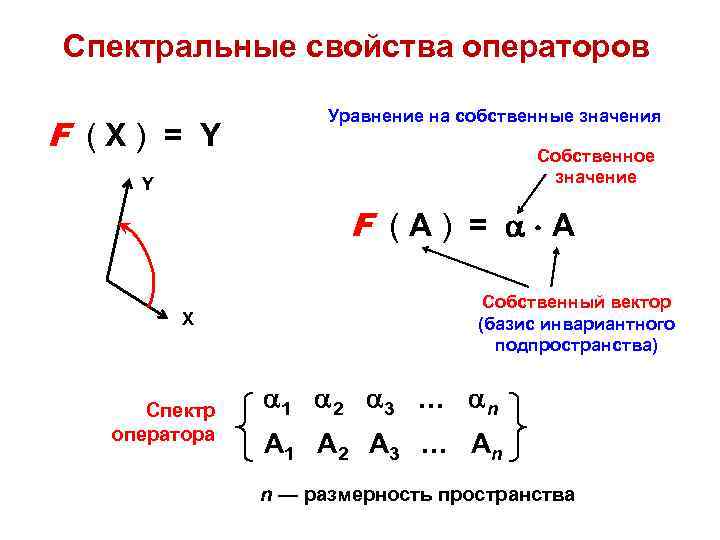Спектральные свойства операторов F (X) = Y Уравнение на собственные значения Собственное значение Y F (А) = А X Спектр оператора Собственный вектор (базис инвариантного подпространства) 1 2 3 … n A 1 A 2 A 3 … A n n — размерность пространства

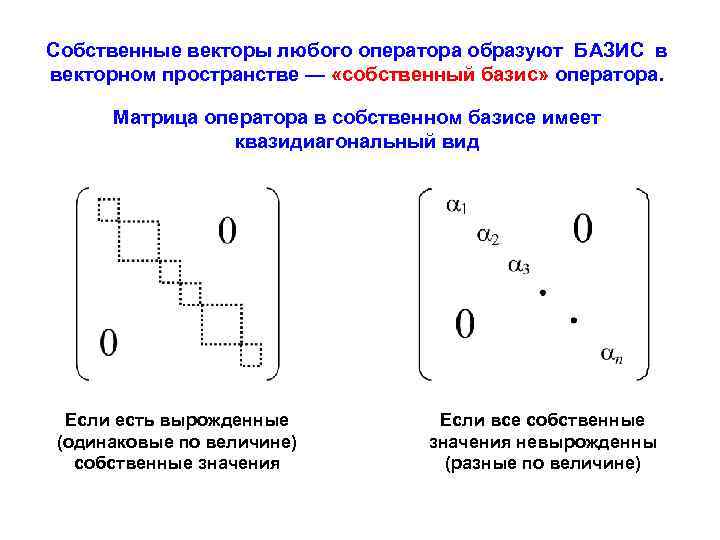Собственные векторы любого оператора образуют БАЗИС в векторном пространстве — «собственный базис» оператора. Матрица оператора в собственном базисе имеет квазидиагональный вид Если есть вырожденные (одинаковые по величине) собственные значения Если все собственные значения невырожденны (разные по величине)

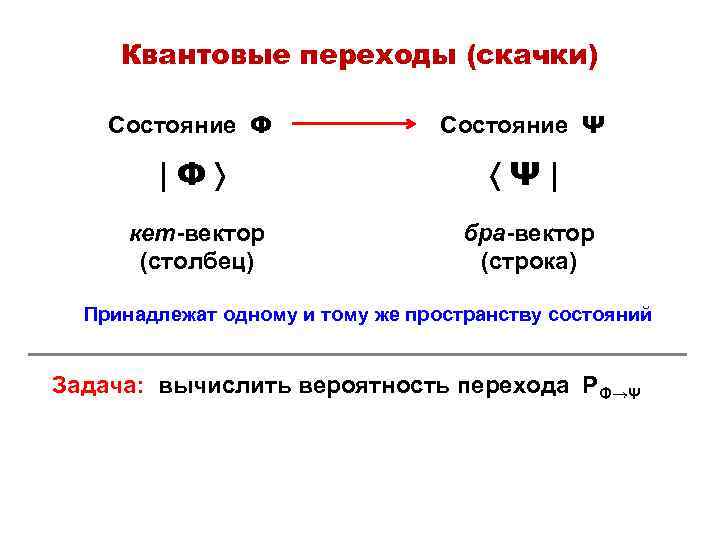Квантовые переходы (скачки) Состояние Φ Состояние Ψ |Φ Ψ| кет-вектор (столбец) бра-вектор (строка) Принадлежат одному и тому же пространству состояний Задача: вычислить вероятность перехода РΦ→Ψ

Решение: вероятность перехода равна квадрату модуля АМПЛИТУДЫ перехода А Φ→Ψ РΦ→Ψ = | AΦ→Ψ |2 Правило: амплитуда перехода А Φ→Ψ равна скалярному произведению векторов начального и конечного состояний АΦ→Ψ = Ψ | Φ Если известны все векторы состояний (пространство состояний), то известны и все амплитуды (и вероятности) переходов между ними.

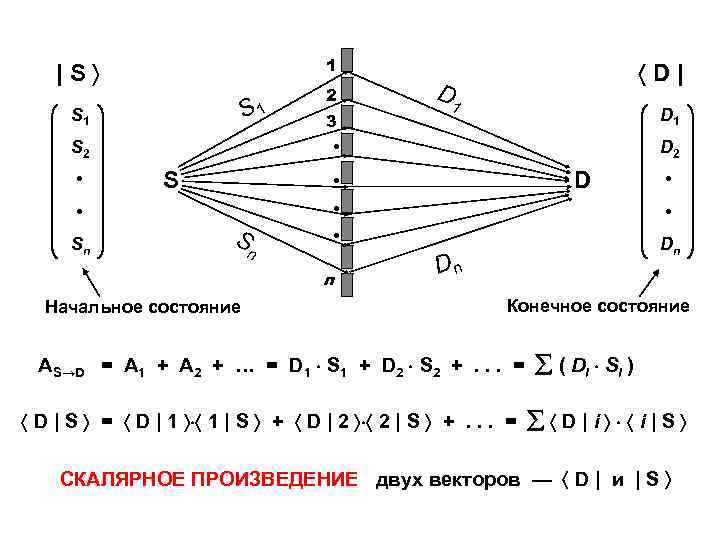1 |S S 1 S 1 D 2 D • • • Sn 3 D • S 2 • 2 D| S n Начальное состояние • • n • Dn Dn Конечное состояние АS→D = А 1 + А 2 + … = D 1 S 1 + D 2 S 2 +. . . = D | S = D | 1 1 | S + D | 2 2 | S +. . . = ( Di S i ) D|i i|S СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ двух векторов — D | и | S

30. 09. 2015

Задача: найти вероятности всех возможных переходов между состояниями Правило: амплитуда перехода А Φ→Ψ равна скалярному произведению векторов начального и конечного состояний АΦ→Ψ = Ψ | Φ РΦ→Ψ = | AΦ→Ψ |2 Для вычисления скалярного произведения нужно знать координаты векторов

Координатные представления векторов состояния Проблема: для вычисления амплитуд переходов необходимо знать координаты векторов начального и конечного состояний Задача: как установить координаты вектора некоторого состояния? Решение: использование спектральных анализаторов

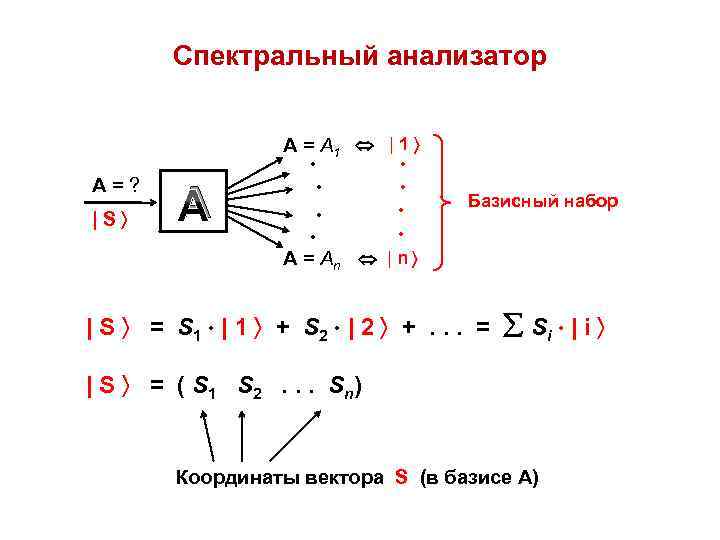Спектральный анализатор А = А 1 | 1 • • А=? |S • • А • • • Базисный набор • А = Аn | S = S 1 | 1 + S 2 | 2 +. . . = Si | S = ( S 1 S 2. . . S n) Координаты вектора S (в базисе А)

Принцип суперпозиции любой вектор может быть представлен в виде линейной комбинации базисных векторов | S = S 1 | 1 + S 2 | 2 +. . . = Si | i S | = 1 | S*1 + 2 | S*2 +. . . = i | S*i Физический смысл координат Si = i | S — амплитуда перехода частицы из начального состояния | S в конечное состояние i | (т. е. в i-е базисное состояние прибора-анализатора) S*i = i | S — амплитуда перехода частицы из i-го базисного состояния прибора-анализатора в состояние | S

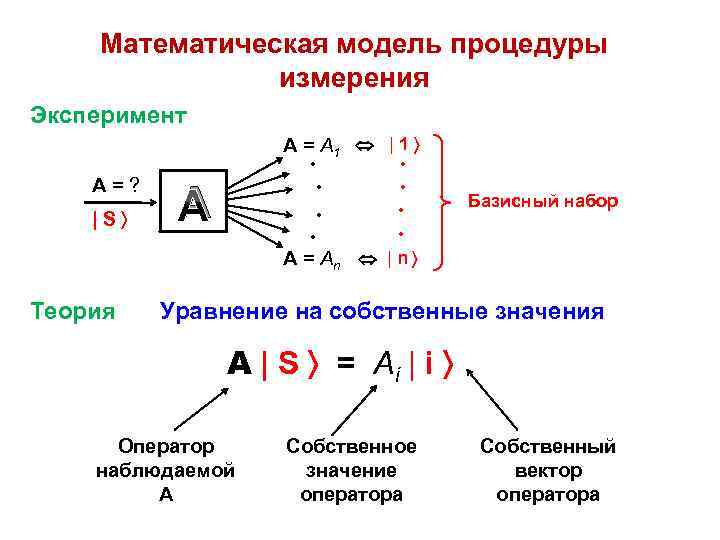Математическая модель процедуры измерения Эксперимент А = А 1 | 1 • • А=? |S • • А • • • Базисный набор • А = Аn | n Теория Уравнение на собственные значения А | S = Ai | i Оператор наблюдаемой А Собственное значение оператора Собственный вектор оператора

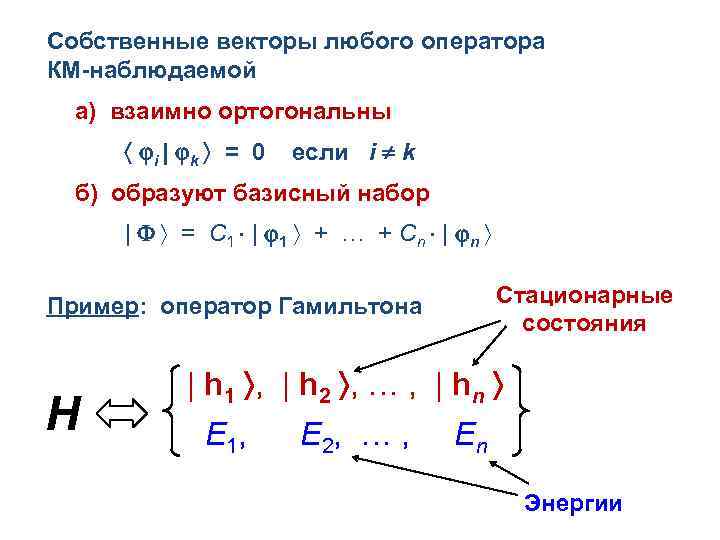Собственные векторы любого оператора КМ-наблюдаемой а) взаимно ортогональны i | k = 0 если i k б) образуют базисный набор | = С 1 | 1 + … + С n | n Стационарные состояния Пример: оператор Гамильтона Н | h 1 , | h 2 , … , | hn E 1, E 2, … , En Энергии

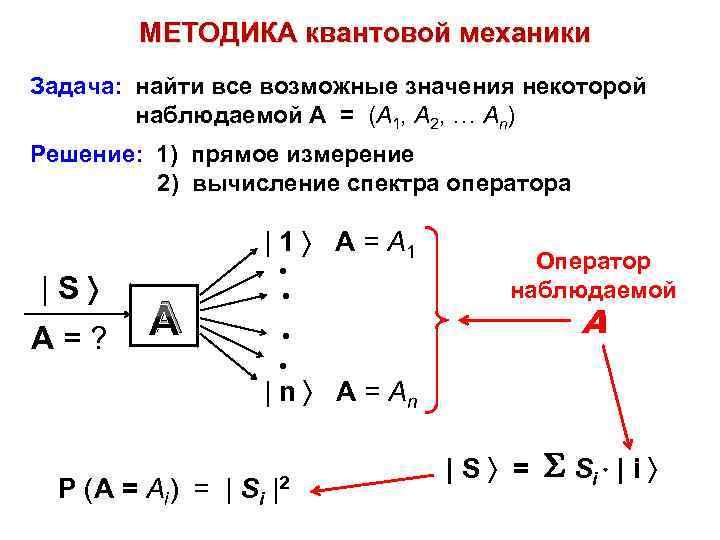МЕТОДИКА квантовой механики Задача: найти все возможные значения некоторой наблюдаемой А = (А 1, А 2, … Аn) Решение: 1) прямое измерение 2) вычисление спектра оператора | 1 A = A 1 |S A=? • • А Оператор наблюдаемой А • • | n A = An P (A = Ai) = | Si |2 |S = Si | i

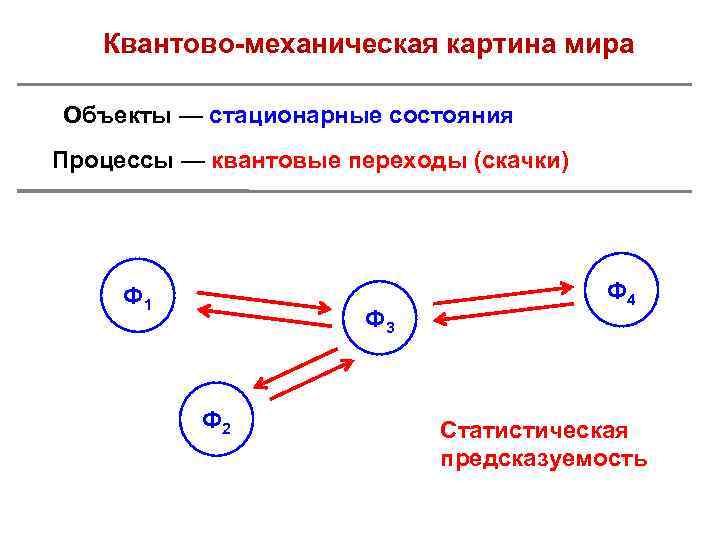Квантово-механическая картина мира Объекты — стационарные состояния Процессы — квантовые переходы (скачки) Ф 1 Ф 3 Ф 2 Ф 4 Статистическая предсказуемость

Задача № 1: установить все возможные состояния (ПРОСТРАНСТВО СОСТОЯНИЙ) исследуемого объекта (атома, молекулы, кристалла и т. д. ) Решение: собственные векторы о КМ-операторов и их линейные комбинации Задача № 2: найти вероятности всех возможных переходов между состояниями Решение: скалярные произведения векторов состояния

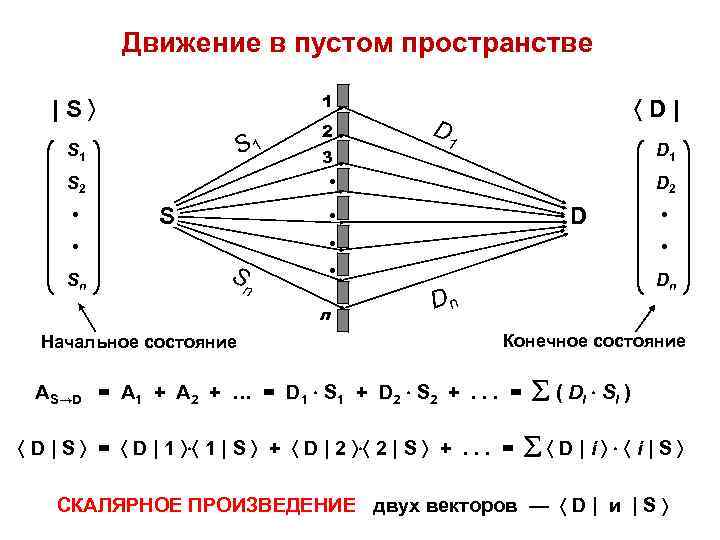Движение в пустом пространстве 1 |S S 1 S 1 D 2 D • • • Sn 3 D • S 2 • 2 D| S n Начальное состояние • • n • Dn Dn Конечное состояние АS→D = А 1 + А 2 + … = D 1 S 1 + D 2 S 2 +. . . = D | S = D | 1 1 | S + D | 2 2 | S +. . . = ( Di S i ) D|i i|S СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ двух векторов — D | и | S

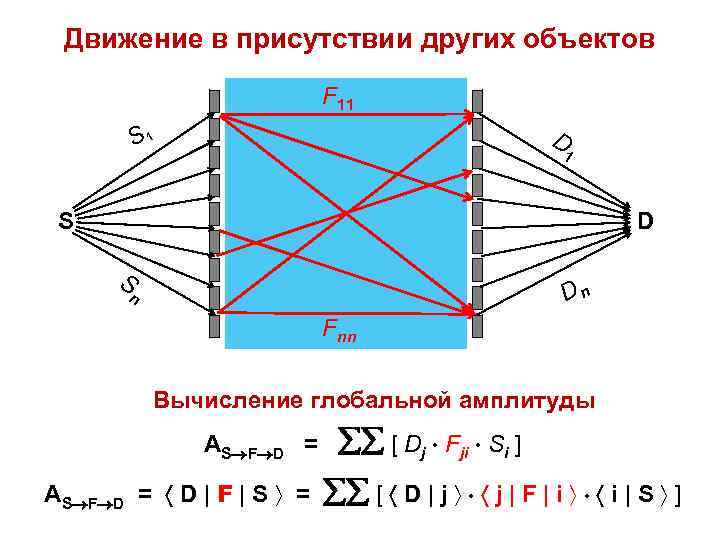Движение в присутствии других объектов F 11 D S 1 1 S Dn n Fnn Вычисление глобальной амплитуды АS F D = D | F | S = [ Dj Fji Si ] [ D | j j | F | i i | S ]

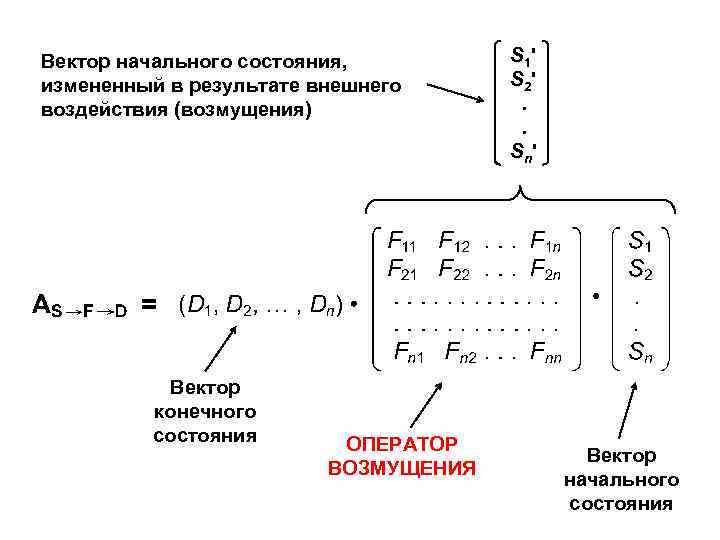Вектор начального состояния, измененный в результате внешнего воздействия (возмущения) Вектор конечного состояния ОПЕРАТОР ВОЗМУЩЕНИЯ S 1 ' S 2 '. . Sn ' Вектор начального состояния

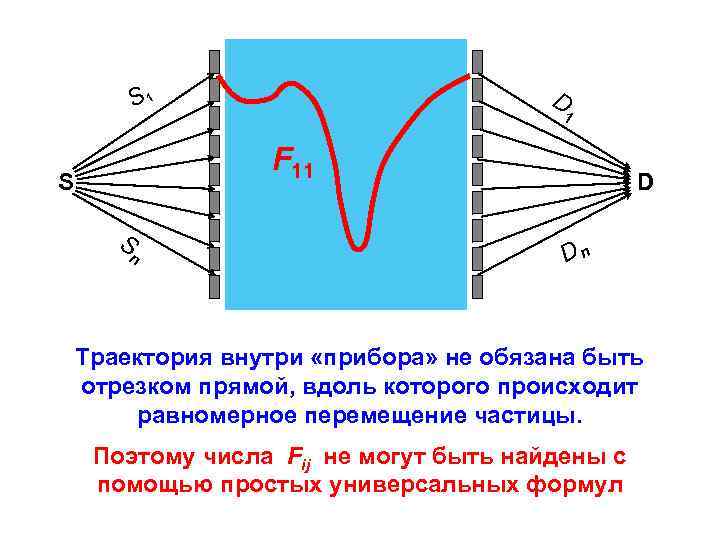D S 1 1 F 11 S S n D Dn Траектория внутри «прибора» не обязана быть отрезком прямой, вдоль которого происходит равномерное перемещение частицы. Поэтому числа Fij не могут быть найдены с помощью простых универсальных формул

Явный вид оператора зависит от выбранного базиса b = F • a 1 -й базис ( b )1 = ( F )1 • ( a )1 U 12 2 -й базис U 21 U 12 U 21 ( b )2 = ( F )2 • ( a )2

Связь между представлениями оператора F ( F )1 = U 12 • ( F )2 • U 21 ( F )2 = U 21 • ( F )1 • U 12 = (U 21)– 1 = (U 21)+ U 21 = (U 12)– 1 = (U 12)+ Унитарные операторы

ВЫВОД В квантовой механике используют три разновидности операторов 1. Операторы наблюдаемых Применение а) вычисление допустимых значений наблюдаемых (собственные значения), б) использование собственных вектров в качестве базисных наборов для анализа векторов состояния

2. Операторы возмущения Применение Описание влияния внешних тел или полей (электромагнитных, гравитационных и др. ) на движение частиц 3. Унитарные операторы Применение Преобразование вычислительных формул при переходе от одной координатной системы к другой