Основы аналитической геометрии 1. Уравнение прямой на плоскости

Основы аналитической геометрии

1. Уравнение прямой на плоскости

Если радиус-векторы точек М0 и М обозначить через и соответственно, то уравнение (1) можно записать в виде Уравнения (1) и (2) называются векторно-параметрическими уравнениями прямой, проходящей через точку М0 и имеющей направляющий вектор .

В координатной записи уравнение (1) имеет вид: или Система уравнений (3) называется параметрическим уравнением прямой, проходящей через точку М0(x0, y0) и имеющей направляющий вектор .

Параметрическое уравнение (3) равносильно уравнению, которое называется каноническим уравнением прямой на плоскости. Замечание: в каноническом уравнении (4) допускаются значения а1 = 0 или а2=0. это не означает, что можно выполнить деление на 0. Из канонического уравнения получаем информацию о том, что направляющий вектор прямой имеет координаты, из которых одна нулевая. Причем в случает а1 = 0 уравнение прямой имеет вид x - x0 = 0 или x = x0, а в случае а2 = 0 уравнение прямой имеет вид y - y0 = 0 или y = y0. y x O y0 y = y0

Задача. Написать уравнение прямой, проходящей через две точки М0(x0, y0) и М1(x1, y1) . Решение: вектор является направляющим вектором прямой. Значит, прямая, проходящая через заданные две точки М0(x0, y0) и М1(x1, y1) - это та же прямая, которая проходит через точку М0(x0, y0) и имеет направляющий вектор . Уравнение этой прямой по формуле (4) имеет вид: Уравнение (5) и есть уравнение прямой, проходящей через две точки М0(x0, y0) и М1(x1, y1). М0(x0, y0) М1(x1, y1)

Теорема. Всякая прямая на плоскости задается некоторым уравнение первого порядка от двух переменных x и y и, наоборот, любое такое уравнение является уравнением некоторой прямой на плоскости. Уравнение (6) называется общим уравнением прямой на плоскости. Замечание: Вектор является направляющим вектором прямой, заданной общим уравнением.

Замечание. Пусть в общем уравнении прямой (6) коэффициент В≠0. Тогда уравнение (6) можно представить в виде или Где Число k называется угловым коэффициентом прямой, а уравнение (7) – уравнением прямой с угловым коэффициентом. Т.о. любая прямая, не параллельная оси Оy (В≠0), может быть задана уравнением с угловым коэффициентом.

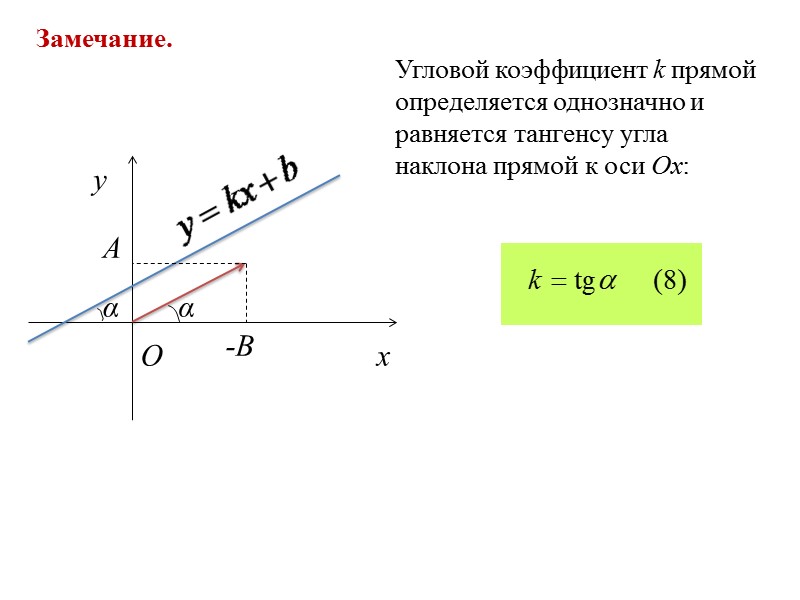
Замечание. Угловой коэффициент k прямой определяется однозначно и равняется тангенсу угла наклона прямой к оси Ox:

2. Нормальный вектор прямой. Расстояние от точки до прямой

Опр. Если вектор перпендикулярен направляющему вектору прямой l, то он называется нормальным вектором прямой l. y x O l

Теорема. Пусть прямая задана общим уравнением: Тогда вектор является нормальным вектором этой прямой.

Задача. Найти уравнение прямой l, которая проходит через точку М0(x0, y0) и имеет нормальный вектор . Решение: Возьмем на прямой l произвольную точку М(x, y) и рассмотрим вектор . Т.к. векторы перпендикулярны, то их скалярное произведение равно нулю: , т.е. Уравнение (8) называется уравнением прямой, проходящей через точку М0(x0, y0) перпендикулярно вектору . y x O М0(x0, y0) М(x, y)

Теорема. Расстояние d от точки М0(x0, y0) до прямой, заданной общим уравнением вычисляется формулой

Задача. Найти расстояние от точки М0(1, 5) до прямой, заданной общим уравнением 3x – 4y – 3 = 0. Решение: По формуле (9) имеем

3. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых

Пусть l1 и l2 – две произвольные прямые на плоскости. Опр. Углом между двумя прямыми l1 и l2 на плоскости называется угол между их направляющими векторами.

Пусть l1 и l2 заданы общими уравнениями: - направляющие векторы. Тогда косинус угла между прямыми вычисляется по формуле:

условие параллельности прямых: прямые l1 и l2 параллельны, если их направляющие векторы коллинеарны, т.е. координаты этих векторов пропорциональны условие перпендикулярности прямых: прямые l1 и l2 перпендикулярны, если нормальные векторы ортогональны, т.е.

если прямые l1 и l2 - не параллельны оси Oy и заданы уравнениями с угловым коэффициентом (7): Тогда угол между двумя прямыми определяется формулой: Две прямые параллельны тогда и только тогда, когда тангенс угла между ними равен нулю: tgφ=0, т.е. выполняется равенство k1 = k2. Прямые l1 и l2 перпендикулярны тогда и только тогда, когда φ=π/2, а значит, котангенс угла между ними равен нулю: Отсюда получаем условие перпендикулярности прямых: