OPRACOWAŁA: BARBARA BIEDROŃ~ ~ ~








































































- Размер: 4 Mегабайта
- Количество слайдов: 80
Описание презентации OPRACOWAŁA: BARBARA BIEDROŃ~ ~ ~ по слайдам
 OPRACOWAŁA: BARBARA BIEDROŃ~ ~ ~
OPRACOWAŁA: BARBARA BIEDROŃ~ ~ ~
 Wróć do spisu treści Przejdź do następnego slajdu Wróć do poprzedniego slajdu Wróć do ostatnio wyświetlanego slajdu Znaczenie poszczególnych przycisków: OSTATNIO WYŚWIETLANY Przejdź do testu SPIS TREŚCI Koniec. Otwiera dodatkowe informacje o figurach Ciekawostki
Wróć do spisu treści Przejdź do następnego slajdu Wróć do poprzedniego slajdu Wróć do ostatnio wyświetlanego slajdu Znaczenie poszczególnych przycisków: OSTATNIO WYŚWIETLANY Przejdź do testu SPIS TREŚCI Koniec. Otwiera dodatkowe informacje o figurach Ciekawostki
 Wstęp Wiadomości — wzory Test – zamiana jednost ek Figury w układzie współrzędnych Sprawdzian – projekt ogrod u Wiadomości — jednostki Koniec OSTATNIO WYŚWIETLANYPROGRAM BLOCKCADPROGRAM FIGURY
Wstęp Wiadomości — wzory Test – zamiana jednost ek Figury w układzie współrzędnych Sprawdzian – projekt ogrod u Wiadomości — jednostki Koniec OSTATNIO WYŚWIETLANYPROGRAM BLOCKCADPROGRAM FIGURY
 Prezentacja „Pola powierzchni figur płaskich” została przygotowana jako pomoc dydaktyczna do lekcji matematyki w gimnazjum (klasa I). Można ją wykorzystać w celu utrwalenia wiadomości uczniów na lekcjach powtórzeniowych. SPIS TREŚCI
Prezentacja „Pola powierzchni figur płaskich” została przygotowana jako pomoc dydaktyczna do lekcji matematyki w gimnazjum (klasa I). Można ją wykorzystać w celu utrwalenia wiadomości uczniów na lekcjach powtórzeniowych. SPIS TREŚCI
 SPIS TREŚCI
SPIS TREŚCI
 Równoległobok. Prostokąt Trójkąt Trapez Wielokąt — jest to część płaszczyzny ograniczona łamaną zwyczajną zamkniętą wraz z tą łamaną. Długość tej łamanej to obwód wielokąta. Przykłady wielokątów: Wybierz figurę, a dowiesz się jak obliczamy jej pole i obwód ! Romb Koło Wielokąt Deltoid SPIS TREŚCI
Równoległobok. Prostokąt Trójkąt Trapez Wielokąt — jest to część płaszczyzny ograniczona łamaną zwyczajną zamkniętą wraz z tą łamaną. Długość tej łamanej to obwód wielokąta. Przykłady wielokątów: Wybierz figurę, a dowiesz się jak obliczamy jej pole i obwód ! Romb Koło Wielokąt Deltoid SPIS TREŚCI
 PROSTOKĄT b a aa. Pole i obwód prostokąta: Pole i obwód kwadratu: Pab Obw 2 a 2 b P 2 a Obw 4 a OSTATNIO WYŚWIETLANY
PROSTOKĄT b a aa. Pole i obwód prostokąta: Pole i obwód kwadratu: Pab Obw 2 a 2 b P 2 a Obw 4 a OSTATNIO WYŚWIETLANY
 a. Pole równoległoboku: P Obwód równoległoboku: RÓWNOLEGŁOBOKa h Obw 2 a b bh OSTATNIO WYŚWIETLANY
a. Pole równoległoboku: P Obwód równoległoboku: RÓWNOLEGŁOBOKa h Obw 2 a b bh OSTATNIO WYŚWIETLANY
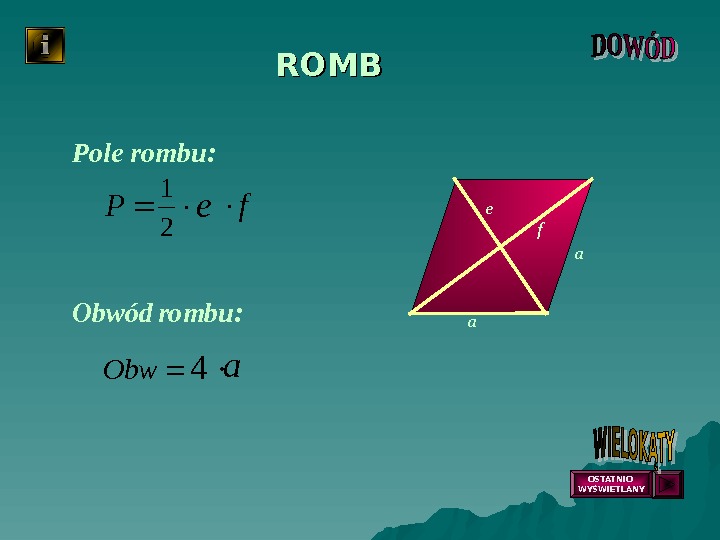
 a ae f. ROMB Pole rombu: Obwód rombu: P 2 1 e f Obw 4 a OSTATNIO WYŚWIETLANY
a ae f. ROMB Pole rombu: Obwód rombu: P 2 1 e f Obw 4 a OSTATNIO WYŚWIETLANY
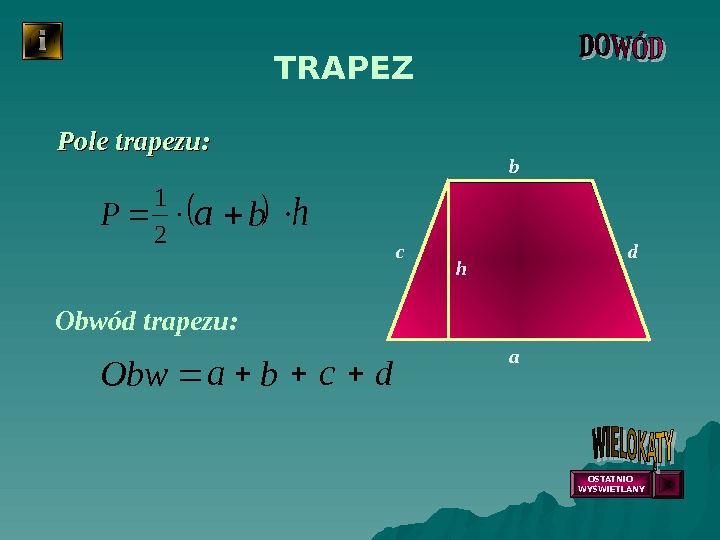
 b ah. Pole trapezu: P TRAPEZ Obwód trapezu: Obw 2 1 ab c d a b cd h OSTATNIO WYŚWIETLANY
b ah. Pole trapezu: P TRAPEZ Obwód trapezu: Obw 2 1 ab c d a b cd h OSTATNIO WYŚWIETLANY
 h bc Obwód trójkąta: Obw Pole trójkąta: TRÓJKĄT a h. P 2 1 ab c a OSTATNIO WYŚWIETLANY
h bc Obwód trójkąta: Obw Pole trójkąta: TRÓJKĄT a h. P 2 1 ab c a OSTATNIO WYŚWIETLANY
 DELTOID Pole deltoidu: P 2 1 ef e fa b Obwód deltoidu: Obw 2 a 2 b OSTATNIO WYŚWIETLANY
DELTOID Pole deltoidu: P 2 1 ef e fa b Obwód deltoidu: Obw 2 a 2 b OSTATNIO WYŚWIETLANY
 Pole koła: P Obw. O r. KOŁO Długość okręgu: 2 r 2 r OSTATNIO WYŚWIETLANY SPIS TREŚCIπ ≈ 3,
Pole koła: P Obw. O r. KOŁO Długość okręgu: 2 r 2 r OSTATNIO WYŚWIETLANY SPIS TREŚCIπ ≈ 3,
 Aby określić, jaką powierzchnię ma figura, możemy podzielić ją na jednakowe kwadraty. Narysowany prostokąt został podzielony na 18 18 jednakowych kwadratów. Mówimy, że jego pole powierzchni, wyrażone za pomocą tych kwadratów, wynosi 18 jednostek. PROSTOKĄTPa 3 2186 aa aa
Aby określić, jaką powierzchnię ma figura, możemy podzielić ją na jednakowe kwadraty. Narysowany prostokąt został podzielony na 18 18 jednakowych kwadratów. Mówimy, że jego pole powierzchni, wyrażone za pomocą tych kwadratów, wynosi 18 jednostek. PROSTOKĄTPa 3 2186 aa aa
 h a Przecinając równoległobok o podstawie a i wysokości h wzdłuż wysokości, otrzymujemy dwie części, z których można złożyć prostokąt o bokach długości a i h. Pole równoległoboku jest równe polu otrzymanego prostokąta. P a h RÓWNOLEGŁOBOK
h a Przecinając równoległobok o podstawie a i wysokości h wzdłuż wysokości, otrzymujemy dwie części, z których można złożyć prostokąt o bokach długości a i h. Pole równoległoboku jest równe polu otrzymanego prostokąta. P a h RÓWNOLEGŁOBOK
 Z dwóch jednakowych rombów o przekątnych długości e i f można ułożyć prostokąt o bokach długości e i f. Prostokąt ten ma pole 2 razy większe niż pole każdego z tych rombów. f e. P 2 1 e f ROMB e f
Z dwóch jednakowych rombów o przekątnych długości e i f można ułożyć prostokąt o bokach długości e i f. Prostokąt ten ma pole 2 razy większe niż pole każdego z tych rombów. f e. P 2 1 e f ROMB e f
 a a b bh Z dwóch jednakowych trapezów o podstawach długości a i b oraz wysokości h można ułożyć równoległobok. Równoległobok ten ma wysokość h, a odpowiadająca tej wysokości podstawa ma długość a+b. Pole trapezu jest 2 razy mniejsze niż pole równoległoboku. P 2 1 abh TRAPEZ
a a b bh Z dwóch jednakowych trapezów o podstawach długości a i b oraz wysokości h można ułożyć równoległobok. Równoległobok ten ma wysokość h, a odpowiadająca tej wysokości podstawa ma długość a+b. Pole trapezu jest 2 razy mniejsze niż pole równoległoboku. P 2 1 abh TRAPEZ
 ah a Z dwóch jednakowych trójkątów o podstawie długości a i wysokości h opuszczonej na tę podstawę można złożyć równoległobok o podstawie a i wysokości h. Pole trójkąta jest 2 razy mniejsze od pola równoległoboku. ah. P 2 1 TRÓJKĄT
ah a Z dwóch jednakowych trójkątów o podstawie długości a i wysokości h opuszczonej na tę podstawę można złożyć równoległobok o podstawie a i wysokości h. Pole trójkąta jest 2 razy mniejsze od pola równoległoboku. ah. P 2 1 TRÓJKĄT
 e f Z dwóch jednakowych deltoidów o przekątnych długości e i f można ułożyć prostokąt o bokach długości e i f. Prostokąt ten ma pole 2 razy większe niż pole każdego z tych deltoidów. P 2 1 ef DELTOID e f
e f Z dwóch jednakowych deltoidów o przekątnych długości e i f można ułożyć prostokąt o bokach długości e i f. Prostokąt ten ma pole 2 razy większe niż pole każdego z tych deltoidów. P 2 1 ef DELTOID e f
 KOŁOP 2 r Popatrz jak można podzielić koło i z otrzymanych części ułożyć figurę przypominającą prostokąt. Długość tego odcinka jest równa długości półokręgu. Pole koła jest równe polu prostokąta o bokach ππ r i r. π rrr
KOŁOP 2 r Popatrz jak można podzielić koło i z otrzymanych części ułożyć figurę przypominającą prostokąt. Długość tego odcinka jest równa długości półokręgu. Pole koła jest równe polu prostokąta o bokach ππ r i r. π rrr
 Prostokąt to czworokąt, który ma wszystkie kąty proste. a = h b bd = h ad 1 2 d Przekątne w prostokącie są równe i dzielą się na połowy Prostokąt ma dwie wysokości, pokrywające się z bokami Wysokość prostokąta to najkrótsza odległość między przeciwległymi bokami 1 2 d Wysokość opuszczona na bok b. Wysokość opuszczona na bok a OSTATNIO WYŚWIETLANY
Prostokąt to czworokąt, który ma wszystkie kąty proste. a = h b bd = h ad 1 2 d Przekątne w prostokącie są równe i dzielą się na połowy Prostokąt ma dwie wysokości, pokrywające się z bokami Wysokość prostokąta to najkrótsza odległość między przeciwległymi bokami 1 2 d Wysokość opuszczona na bok b. Wysokość opuszczona na bok a OSTATNIO WYŚWIETLANY
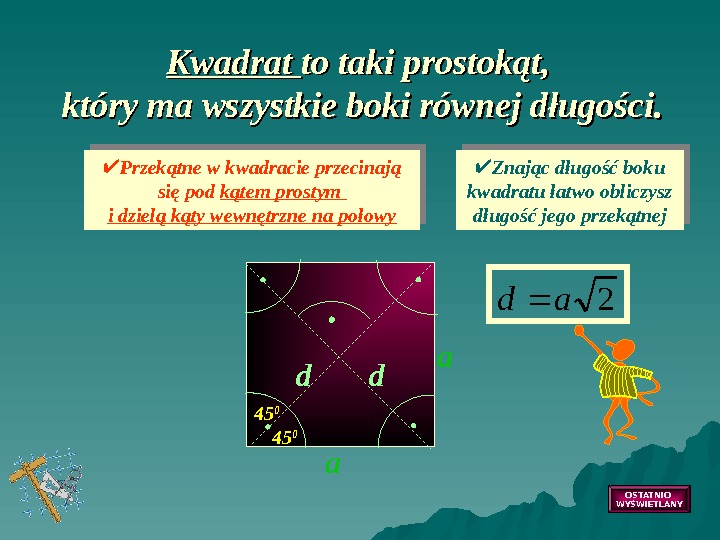
 Kwadrat to taki prostokąt, który ma wszystkie boki równej długości. d d a a Przekątne w kwadracie przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy Znając długość boku kwadratu łatwo obliczysz długość jego przekątnejda 2 45 0 OSTATNIO WYŚWIETLANY
Kwadrat to taki prostokąt, który ma wszystkie boki równej długości. d d a a Przekątne w kwadracie przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy Znając długość boku kwadratu łatwo obliczysz długość jego przekątnejda 2 45 0 OSTATNIO WYŚWIETLANY
 Wysokość równoległoboku to najkrótsza odległość między przeciwległymi bokamib ah a h b d 1 d 2 Przekątne równoległoboku nie są równe, lecz dzielą się na połowy Zauważ, że mówiąc o najkrótszej odległości mamy na myśli długość odcinka prostopadłego do boku wielokąta !Równoległobok to czworokąt, który ma dwie pary boków równoległych. OSTATNIO WYŚWIETLANY
Wysokość równoległoboku to najkrótsza odległość między przeciwległymi bokamib ah a h b d 1 d 2 Przekątne równoległoboku nie są równe, lecz dzielą się na połowy Zauważ, że mówiąc o najkrótszej odległości mamy na myśli długość odcinka prostopadłego do boku wielokąta !Równoległobok to czworokąt, który ma dwie pary boków równoległych. OSTATNIO WYŚWIETLANY
 Romb to taki równoległobok, który ma wszystkie boki równej długości. a a 1 2 1 2 Przekątne w rombie przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy UWAGA: W rombie , podobnie jak w każdym równoległoboku , suma kąta ostrego i kąta rozwartego wynosi 180 0 OSTATNIO WYŚWIETLANY
Romb to taki równoległobok, który ma wszystkie boki równej długości. a a 1 2 1 2 Przekątne w rombie przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy UWAGA: W rombie , podobnie jak w każdym równoległoboku , suma kąta ostrego i kąta rozwartego wynosi 180 0 OSTATNIO WYŚWIETLANY
 Boki równoległe to podstawy , , a dwa pozostałe boki to ramiona trapezu. Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. podstawah d 1 d 2 ram ięWysokość trapezu to najkrótsza odległość między jego podstawami Odcinki d 1 i d 2 to przekątne trapezu OSTATNIO WYŚWIETLANY
Boki równoległe to podstawy , , a dwa pozostałe boki to ramiona trapezu. Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. podstawah d 1 d 2 ram ięWysokość trapezu to najkrótsza odległość między jego podstawami Odcinki d 1 i d 2 to przekątne trapezu OSTATNIO WYŚWIETLANY
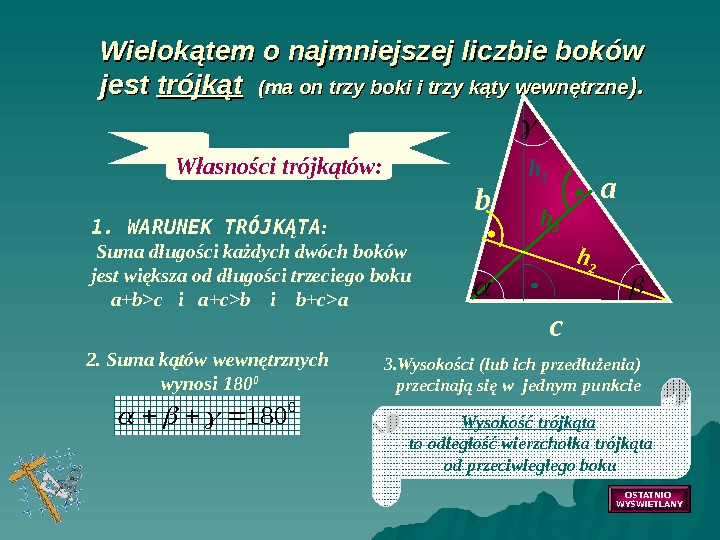
 Wysokość trójkąta to odległość wierzchołka trójkąta od przeciwległego boku. Własności trójkątów: 1. WARUNEK TRÓJKĄTA : Suma długości każdych dwóch boków jest większa od długości trzeciego boku a+b>c i a+c>b i b+c>a. Wielokątem o najmniejszej liczbie boków jest trójkąt (ma on trzy boki i trzy kąty wewnętrzne ). ). h 3 h 1 h 2 180 0 2. Suma kątów wewnętrznych wynosi 180 0 3. Wysokości (lub ich przedłużenia) przecinają się w jednym punkcie a b c OSTATNIO WYŚWIETLANY
Wysokość trójkąta to odległość wierzchołka trójkąta od przeciwległego boku. Własności trójkątów: 1. WARUNEK TRÓJKĄTA : Suma długości każdych dwóch boków jest większa od długości trzeciego boku a+b>c i a+c>b i b+c>a. Wielokątem o najmniejszej liczbie boków jest trójkąt (ma on trzy boki i trzy kąty wewnętrzne ). ). h 3 h 1 h 2 180 0 2. Suma kątów wewnętrznych wynosi 180 0 3. Wysokości (lub ich przedłużenia) przecinają się w jednym punkcie a b c OSTATNIO WYŚWIETLANY
 Deltoid to czworokąt, który ma dwie pary sąsiednich boków równej długości. a a b b d 1 d 2 Przekątne deltoidu są prostopadłe. Punkt przecięcia przekątnych dzieli jedną z nich na połowy. Pdd 1 2 12 Deltoid nazywamy latawcem. OSTATNIO WYŚWIETLANY
Deltoid to czworokąt, który ma dwie pary sąsiednich boków równej długości. a a b b d 1 d 2 Przekątne deltoidu są prostopadłe. Punkt przecięcia przekątnych dzieli jedną z nich na połowy. Pdd 1 2 12 Deltoid nazywamy latawcem. OSTATNIO WYŚWIETLANY
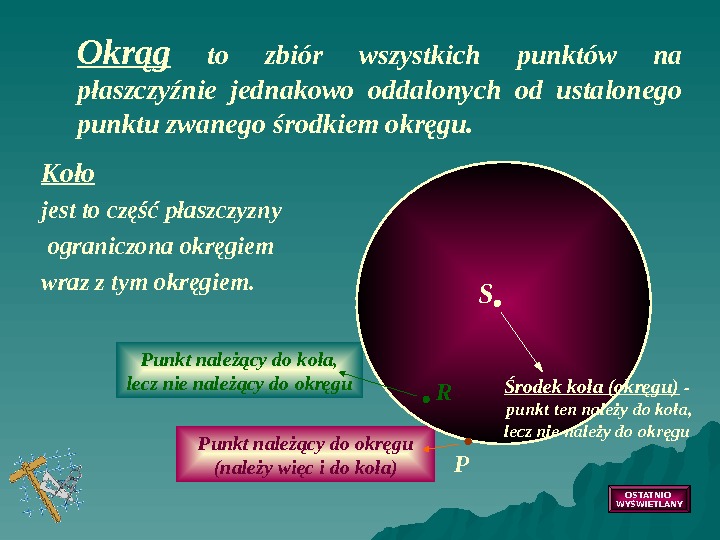
 Punkt należący do koła, lecz nie należący do okręgu Punkt należący do okręgu (należy więc i do koła)Koło jest to część płaszczyzny ograniczona okręgiem wraz z tym okręgiem. PR S Środek koła (okręgu) — punkt ten należy do koła, lecz nie należy do okręgu OSTATNIO WYŚWIETLANYOkrąg to zbiór wszystkich punktów na płaszczyźnie jednakowo oddalonych od ustalonego punktu zwanego środkiem okręgu.
Punkt należący do koła, lecz nie należący do okręgu Punkt należący do okręgu (należy więc i do koła)Koło jest to część płaszczyzny ograniczona okręgiem wraz z tym okręgiem. PR S Środek koła (okręgu) — punkt ten należy do koła, lecz nie należy do okręgu OSTATNIO WYŚWIETLANYOkrąg to zbiór wszystkich punktów na płaszczyźnie jednakowo oddalonych od ustalonego punktu zwanego środkiem okręgu.
 Klasyfikacja czworokątów. P r o s t o k ą t y m a j ą p r o s t e k ą t y K w a d r a t y R o m b y m a j ą r ó w n e b o k i R ó w n o l e g ł o b o k i m a j ą d w i e p a r y b o k ó w r ó w n o l e g ł y c h P r z y k ł a d y t r a p e z ó w — r ó w n o r a m i e n n y — p r o s t o k a t n y T r a p e z y m a j ą c o n a j m n i e j j e d n ą p a r ę b o k ó w r ó w n o l e g ł y c h I n n e n p. d e l t o i d C z w o r o k ą t y OSTATNIO WYŚWIETLANY
Klasyfikacja czworokątów. P r o s t o k ą t y m a j ą p r o s t e k ą t y K w a d r a t y R o m b y m a j ą r ó w n e b o k i R ó w n o l e g ł o b o k i m a j ą d w i e p a r y b o k ó w r ó w n o l e g ł y c h P r z y k ł a d y t r a p e z ó w — r ó w n o r a m i e n n y — p r o s t o k a t n y T r a p e z y m a j ą c o n a j m n i e j j e d n ą p a r ę b o k ó w r ó w n o l e g ł y c h I n n e n p. d e l t o i d C z w o r o k ą t y OSTATNIO WYŚWIETLANY
 Obwód wielokąta jest to suma długości wszystkich jego boków a be d c. Obwód tego wielokąta obliczymy dodając długości wszystkich jego boków Obw = a + b + c + d + e OSTATNIO WYŚWIETLANY
Obwód wielokąta jest to suma długości wszystkich jego boków a be d c. Obwód tego wielokąta obliczymy dodając długości wszystkich jego boków Obw = a + b + c + d + e OSTATNIO WYŚWIETLANY
 Pole dowolnego wielokąta łatwo obliczysz, jeśli podzielisz go na dobrze znane Ci figury tak, jak zrobiono to na poniższych przykładach. III II OSTATNIO WYŚWIETLANY
Pole dowolnego wielokąta łatwo obliczysz, jeśli podzielisz go na dobrze znane Ci figury tak, jak zrobiono to na poniższych przykładach. III II OSTATNIO WYŚWIETLANY
 Zobacz w jaki sposób można obliczyć pole dowolnego wielokąta Pole tego pięciokąta = = pole trójkąta + pole trapezu P trapezu. Ptrójkąta Phkta ahab 5222 1 ą h 2 a b h 1 Można zapisać to wzorem: OSTATNIO WYŚWIETLANY
Zobacz w jaki sposób można obliczyć pole dowolnego wielokąta Pole tego pięciokąta = = pole trójkąta + pole trapezu P trapezu. Ptrójkąta Phkta ahab 5222 1 ą h 2 a b h 1 Można zapisać to wzorem: OSTATNIO WYŚWIETLANY
 • Suma kątów wewnętrznych w czworokącie wynosi 360 0 d 1 d 2 360 0 • Każdy czworokąt ma dwie przekątne. Wielokąt, który ma cztery boki to czworokąt OSTATNIO WYŚWIETLANY
• Suma kątów wewnętrznych w czworokącie wynosi 360 0 d 1 d 2 360 0 • Każdy czworokąt ma dwie przekątne. Wielokąt, który ma cztery boki to czworokąt OSTATNIO WYŚWIETLANY
 SPIS TREŚCI
SPIS TREŚCI
 ZALEŻNOŚCI MIĘDZY JEDNOSTKAMI POLA: 1 km 2 = 100000 cm 2 1 km 2 = 1000000 m 21 km 2 = 10000 dm 2 1 dm 2 = 100 cm 2 1 dm 2 = 10000 mm 2 1 dm 2 = 0, 01 m 2 1 a = 100 m 2 1 ha = 10000 m 2 1 m 2 = 0, 01 a = 0, 0001 ha OSTATNIO WYŚWIETLANY
ZALEŻNOŚCI MIĘDZY JEDNOSTKAMI POLA: 1 km 2 = 100000 cm 2 1 km 2 = 1000000 m 21 km 2 = 10000 dm 2 1 dm 2 = 100 cm 2 1 dm 2 = 10000 mm 2 1 dm 2 = 0, 01 m 2 1 a = 100 m 2 1 ha = 10000 m 2 1 m 2 = 0, 01 a = 0, 0001 ha OSTATNIO WYŚWIETLANY
 1 cm 2 — jest to kwadrat o boku 1 cm 1 dm 2 — — jest to kwadrat o boku 1 dm (10 cm) 1 m 2 — jest to kwadrat o boku 1 m 1 km 2 -jest to kwadrat o boku 1 km 1 a (ar) — jest to kwadrat o boku 10 m 1 ha (hektar) — jest to kwadrat o boku 100 m. Jednostki, w których mierzymy pole figury to kwadraty: 1 cm 2 Pcm 27 21 mm 2 — jest to kwadrat o boku 1 mm OSTATNIO WYŚWIETLANY
1 cm 2 — jest to kwadrat o boku 1 cm 1 dm 2 — — jest to kwadrat o boku 1 dm (10 cm) 1 m 2 — jest to kwadrat o boku 1 m 1 km 2 -jest to kwadrat o boku 1 km 1 a (ar) — jest to kwadrat o boku 10 m 1 ha (hektar) — jest to kwadrat o boku 100 m. Jednostki, w których mierzymy pole figury to kwadraty: 1 cm 2 Pcm 27 21 mm 2 — jest to kwadrat o boku 1 mm OSTATNIO WYŚWIETLANY
 Zamiana jednostek pola Przykłady: 1 cm 2 = (10 mm) 2 = 100 mm 2 1 dm 2 = (10 cm) 2 = 100 cm 2 1 m 2 = (100 cm) 2 = 10 000 cm 2 1 m 2 = (10 dm) 2 = 100 dm 2 1 km 2 = (1000 m) 2 = 1 000 m 2 1 a = (10 m) 2 = 100 m 2 1 ha = (100 m) 2 = 10 000 m 2 1 ha = 10000 m 2 100 m 1 a = 100 m 2 10 m OSTATNIO WYŚWIETLANY
Zamiana jednostek pola Przykłady: 1 cm 2 = (10 mm) 2 = 100 mm 2 1 dm 2 = (10 cm) 2 = 100 cm 2 1 m 2 = (100 cm) 2 = 10 000 cm 2 1 m 2 = (10 dm) 2 = 100 dm 2 1 km 2 = (1000 m) 2 = 1 000 m 2 1 a = (10 m) 2 = 100 m 2 1 ha = (100 m) 2 = 10 000 m 2 1 ha = 10000 m 2 100 m 1 a = 100 m 2 10 m OSTATNIO WYŚWIETLANY
 ZALEŻNOŚCI MIĘDZY JEDNOSTKAMI DŁUGOŚCI: 1 km = 1000 m 1 m = 100 cm 1 m = 10 dm 1 dm = 10 cm 1 cm = 10 mm OSTATNIO WYŚWIETLANY SPIS TREŚCI
ZALEŻNOŚCI MIĘDZY JEDNOSTKAMI DŁUGOŚCI: 1 km = 1000 m 1 m = 100 cm 1 m = 10 dm 1 dm = 10 cm 1 cm = 10 mm OSTATNIO WYŚWIETLANY SPIS TREŚCI
 — PROJEKT OGRODU OTWÓRZ SPIS TREŚCI
— PROJEKT OGRODU OTWÓRZ SPIS TREŚCI
 1 2 4 5 6 789 10 1 1 3 OTO PROJEKT DZIAŁKI Przyj się rysunkowi, a następnie wykonaj ćwiczenia. 12 13 Powrót 11 Powrót 22 Powrót 33 Powrót 44 OSTATNIO WYŚWIETLANYOBLICZENIAOBJAŚNIENIA DO RYSUNKU ĆWICZWNI
1 2 4 5 6 789 10 1 1 3 OTO PROJEKT DZIAŁKI Przyj się rysunkowi, a następnie wykonaj ćwiczenia. 12 13 Powrót 11 Powrót 22 Powrót 33 Powrót 44 OSTATNIO WYŚWIETLANYOBLICZENIAOBJAŚNIENIA DO RYSUNKU ĆWICZWNI
 Działka ma powierzchnię: 80 m 2 8 a 0, 8 ha OBLICZENI
Działka ma powierzchnię: 80 m 2 8 a 0, 8 ha OBLICZENI
 Jaką powierzchnię ma budynek? 98 m 2 9, 8 m 2 0, 098 a OBLICZENI
Jaką powierzchnię ma budynek? 98 m 2 9, 8 m 2 0, 098 a OBLICZENI
 Jaką powierzchnię zajmuje basen i oczko wodne? ok. 0, 2 a ok. 2000 m 2 ok. 20 m 2 OBLICZENI
Jaką powierzchnię zajmuje basen i oczko wodne? ok. 0, 2 a ok. 2000 m 2 ok. 20 m 2 OBLICZENI
 Jaką powierzchnię zajmuje altana? 20, 25 m 2 202, 5 cm 2 20, 25 dm 2 OBLICZENI
Jaką powierzchnię zajmuje altana? 20, 25 m 2 202, 5 cm 2 20, 25 dm 2 OBLICZENI
 Jaką powierzchnię zajmują wszystkie ogródki i rabaty? 370 m 2 3, 7 a 0, 37 a OBLICZENI
Jaką powierzchnię zajmują wszystkie ogródki i rabaty? 370 m 2 3, 7 a 0, 37 a OBLICZENI
 Na jakiej powierzchni trawnika leży latawiec? 20 dm 2 20000 cm 2 2 m 2 OBLICZENI
Na jakiej powierzchni trawnika leży latawiec? 20 dm 2 20000 cm 2 2 m 2 OBLICZENI
 Jaką powierzchnię zajmuje ścieżka? 4 m 2 400 dm 2 OBLICZENI
Jaką powierzchnię zajmuje ścieżka? 4 m 2 400 dm 2 OBLICZENI
 Jaką powierzchnię zajmują dwa wjazdy i podjazd? 250 m 2 0, 25 a 0, 025 ha OBLICZENI
Jaką powierzchnię zajmują dwa wjazdy i podjazd? 250 m 2 0, 25 a 0, 025 ha OBLICZENI
 ĆWICZENI
ĆWICZENI
 Ile metrów kwadratowych mają razem: wjazd 1 i wjazd 2? 230 32 23 OBLICZENI
Ile metrów kwadratowych mają razem: wjazd 1 i wjazd 2? 230 32 23 OBLICZENI
 Jaką powierzchnię działki należy zasiać trawą? ok. 600 a ok. 0, 06 haok. 60 m 2 OBLICZENI
Jaką powierzchnię działki należy zasiać trawą? ok. 600 a ok. 0, 06 haok. 60 m 2 OBLICZENI
 Oblicz koszt zakupu jednej kostki brukowej każdego koloru. Wymiary: 10 cm x 20 cm Cena za 1 m 2 27 zł. Wymiary: 10 cm x 20 cm Cena za 1 m 2 29 zł. 1 m 2 chodnika składamy z 50 kostek. Pamiętaj, że cena 1 m 2 chodnika zależy od ilości kostek każdego koloru. ! OSTATNIO WYŚWIETLANY
Oblicz koszt zakupu jednej kostki brukowej każdego koloru. Wymiary: 10 cm x 20 cm Cena za 1 m 2 27 zł. Wymiary: 10 cm x 20 cm Cena za 1 m 2 29 zł. 1 m 2 chodnika składamy z 50 kostek. Pamiętaj, że cena 1 m 2 chodnika zależy od ilości kostek każdego koloru. ! OSTATNIO WYŚWIETLANY
 Wymiary: 10 cm x 20 cm Cena za 1 m 2 29 zł. CZERWONA KOSTKA 1 szt. kosztuje: 0, 58 zł 5, 80 zł 0, 85 zł
Wymiary: 10 cm x 20 cm Cena za 1 m 2 29 zł. CZERWONA KOSTKA 1 szt. kosztuje: 0, 58 zł 5, 80 zł 0, 85 zł
 Wymiary: 10 cm x 20 cm Cena za 1 m 2 27 zł. SZARA KOSTKA 1 szt. kosztuje: 5, 4 zł 0, 45 zł 0, 54 zł
Wymiary: 10 cm x 20 cm Cena za 1 m 2 27 zł. SZARA KOSTKA 1 szt. kosztuje: 5, 4 zł 0, 45 zł 0, 54 zł
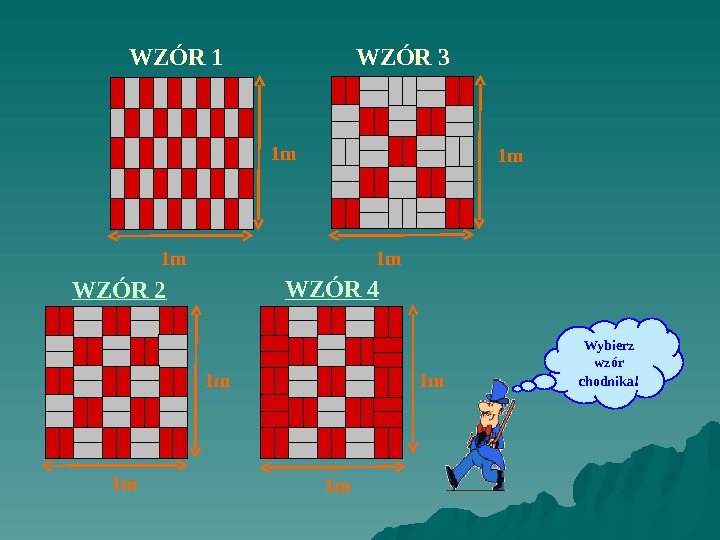
 1 m 1 m. WZÓR 2 Wybierz wzór chodnika !WZÓR 1 1 m 1 m. WZÓR 3 1 m 1 m. WZÓR
1 m 1 m. WZÓR 2 Wybierz wzór chodnika !WZÓR 1 1 m 1 m. WZÓR 3 1 m 1 m. WZÓR
 644 zł 310, 50 złWybierając wzór 1, koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 1 333, 50 zł
644 zł 310, 50 złWybierając wzór 1, koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 1 333, 50 zł
 644, 92 zł694, 42 zł Wybierając wzór 2 koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 2 346, 84 zł
644, 92 zł694, 42 zł Wybierając wzór 2 koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 2 346, 84 zł
 637, 56 zł673, 56 zł Wybierając wzór 3 koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 3 397, 44 zł
637, 56 zł673, 56 zł Wybierając wzór 3 koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 3 397, 44 zł
 453, 56 zł652, 28 zł Wybierając wzór 4, koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 4 283, 60 zł
453, 56 zł652, 28 zł Wybierając wzór 4, koszt zakupu kostki brukowej na wjazd 1 i wjazd 2 wynosi: WZÓR 4 283, 60 zł
 TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha 1 m 1 m 2 2 chodnika (wzór 1) obejmuje: 25 kostek czerwonych (1 szt. 0, 58 zł) i 25 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 644 zł. KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 2 SPIS TREŚCIWZÓR
TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha 1 m 1 m 2 2 chodnika (wzór 1) obejmuje: 25 kostek czerwonych (1 szt. 0, 58 zł) i 25 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 644 zł. KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 2 SPIS TREŚCIWZÓR
 TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 m 1 m 2 2 chodnika (wzór 2) obejmuje: 26 kostek czerwonych (1 szt. 0, 58 zł) i 24 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 644, 92 zł. 1 2 SPIS TREŚCIWZÓR
TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 m 1 m 2 2 chodnika (wzór 2) obejmuje: 26 kostek czerwonych (1 szt. 0, 58 zł) i 24 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 644, 92 zł. 1 2 SPIS TREŚCIWZÓR
 TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 m 1 m 2 2 chodnika (wzór 3) obejmuje: 18 kostek czerwonych (1 szt. 0, 58 zł) i 32 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 637, 56 zł. 1 2 SPIS TREŚCIWZÓR
TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 m 1 m 2 2 chodnika (wzór 3) obejmuje: 18 kostek czerwonych (1 szt. 0, 58 zł) i 32 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 637, 56 zł. 1 2 SPIS TREŚCIWZÓR
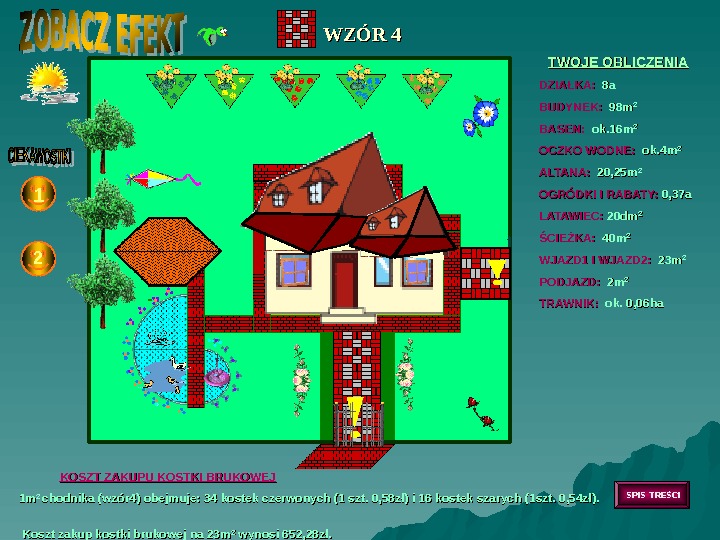
 TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 m 1 m 2 2 chodnika (wzór 4) obejmuje: 34 kostek czerwonych (1 szt. 0, 58 zł) i 16 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 652, 28 zł. 1 2 SPIS TREŚCIWZÓR
TWOJE OBLICZENIA DZIAŁKA: 8 a 8 a BUDYNEK: 98 m 22 BASEN: ok. 16 m 22 OCZKO WODNE: ok. 4 m 22 ALTANA: 20, 25 m 22 OGRÓDKI I RABATY: 0, 37 a LATAWIEC: 20 dm 22 ŚCIEŻKA: 40 m 22 WJAZD 1 I WJAZD 2: 23 m 22 PODJAZD: 2 m 2 m 22 TRAWNIK: ok. 0, 06 ha KOSZT ZAKUPU KOSTKI BRUKOWEJ 1 m 1 m 2 2 chodnika (wzór 4) obejmuje: 34 kostek czerwonych (1 szt. 0, 58 zł) i 16 kostek szarych (1 szt. 0, 54 zł). Koszt zakup kostki brukowej na 23 m 22 wynosi 652, 28 zł. 1 2 SPIS TREŚCIWZÓR
 ROZWIĄZAŁEŚ POPRAWNIE CAŁY TEST ZOBACZ WYNIK SWOJEJ PRACY WEDŁUG WYBRANEGO WZORU KOSTKI WZÓR 1 WZÓR 2 WZÓR 3 WZÓR 4 SPIS TREŚCI
ROZWIĄZAŁEŚ POPRAWNIE CAŁY TEST ZOBACZ WYNIK SWOJEJ PRACY WEDŁUG WYBRANEGO WZORU KOSTKI WZÓR 1 WZÓR 2 WZÓR 3 WZÓR 4 SPIS TREŚCI
 OTWÓR Z SPIS TREŚCI
OTWÓR Z SPIS TREŚCI
 ODCZYTAJ WSPÓŁRZĘDNE ZAZNACZONYCH PUNKTÓW I OBLICZ POLA POWIERZCHNI NARYSOWANYCH FIGUR MASZ OCHOTĘ JESZCZE POĆWICZYĆ? ? ? TAK NI
ODCZYTAJ WSPÓŁRZĘDNE ZAZNACZONYCH PUNKTÓW I OBLICZ POLA POWIERZCHNI NARYSOWANYCH FIGUR MASZ OCHOTĘ JESZCZE POĆWICZYĆ? ? ? TAK NI
 B C D A E F GH I J K L M N R P S T W U X Y Z Ł O xy 1 SPIS TREŚCI
B C D A E F GH I J K L M N R P S T W U X Y Z Ł O xy 1 SPIS TREŚCI
 UWAGA! Podziel równoległobok na dwa trójkąty!B DA C P=24 B DA C P=26 B DA C P=12 C Oy
UWAGA! Podziel równoległobok na dwa trójkąty!B DA C P=24 B DA C P=26 B DA C P=12 C Oy
 E F GH P = 56 E F GH P = 67 E F GH P = 77 C Oy
E F GH P = 56 E F GH P = 67 E F GH P = 77 C Oy
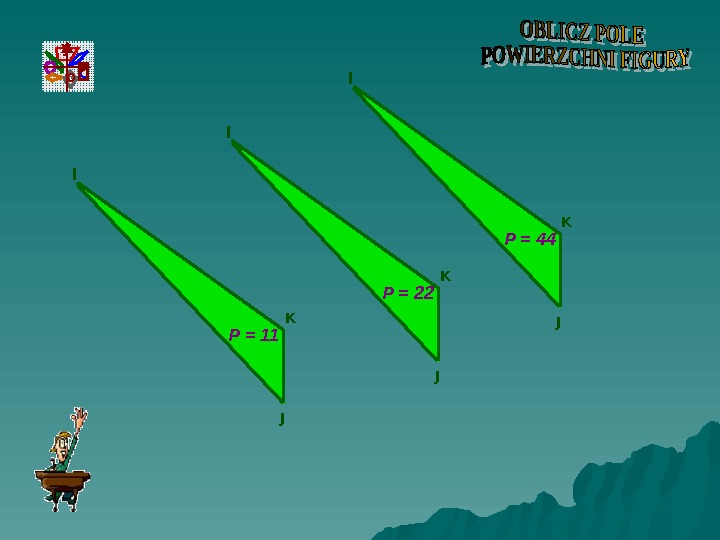
 I J K P = 22 I J K P = 44 I J K P = 11 C Oy
I J K P = 22 I J K P = 44 I J K P = 11 C Oy
 L P ≈≈ 28, 26 UWAGA! ππ ≈≈ 3, 14 L P ≈≈ 28, 66 L P ≈≈ 26, 28 C Oy
L P ≈≈ 28, 26 UWAGA! ππ ≈≈ 3, 14 L P ≈≈ 28, 66 L P ≈≈ 26, 28 C Oy
 MN RPM NR P M N R P P =36 P = 18 P =24 C Oy
MN RPM NR P M N R P P =36 P = 18 P =24 C Oy
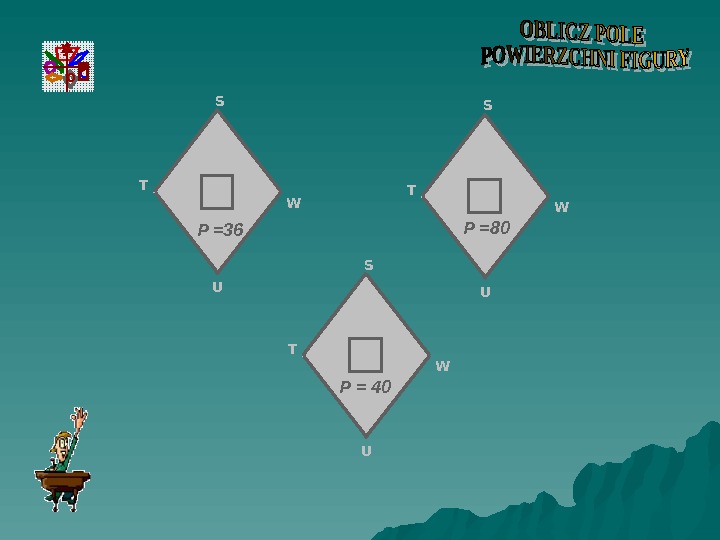
 S T W UP =36 S T W UP = 40 S T W UP =80 C Oy
S T W UP =36 S T W UP = 40 S T W UP =80 C Oy
 X Y Z Ł P = 54 X Y Z Ł P = 45 X Y Z Ł P = 40 C Oy
X Y Z Ł P = 54 X Y Z Ł P = 45 X Y Z Ł P = 40 C Oy
 SPIS TREŚCIWRÓĆ DO ĆWICZEŃ
SPIS TREŚCIWRÓĆ DO ĆWICZEŃ
 C Oy OSTATNIO WYŚWIETLANY
C Oy OSTATNIO WYŚWIETLANY
 OTWÓR Z SPIS TREŚCI
OTWÓR Z SPIS TREŚCI
 KONIEC PREZENTACJI ABY ZAKOŃCZYĆ PRZEGLĄDANIE PREZENTACJI NACIŚNIJ KLAWISZ ESCES
KONIEC PREZENTACJI ABY ZAKOŃCZYĆ PRZEGLĄDANIE PREZENTACJI NACIŚNIJ KLAWISZ ESCES
 OSTATNIO WYŚWIETLANY SPIS TREŚCIDługość odcinka możemy zmierzyć za pomocą linijki. Mało kto wie, ze istnieje przyrząd do mierzenia pól różnych figur. Takie urządzenie, planimetr, wynalazł w roku 1814 niemiecki inżynier J. M. Herman. Mierzenie pola figury polega na prowadzeniu specjalnego wodzika wzdłuż linii ograniczającej tę figurę. Planimetr najczęściej używany jest przez geodetów do mierzenia pól obszarów zaznaczonych na mapie.
OSTATNIO WYŚWIETLANY SPIS TREŚCIDługość odcinka możemy zmierzyć za pomocą linijki. Mało kto wie, ze istnieje przyrząd do mierzenia pól różnych figur. Takie urządzenie, planimetr, wynalazł w roku 1814 niemiecki inżynier J. M. Herman. Mierzenie pola figury polega na prowadzeniu specjalnego wodzika wzdłuż linii ograniczającej tę figurę. Planimetr najczęściej używany jest przez geodetów do mierzenia pól obszarów zaznaczonych na mapie.
 OSTATNIO WYŚWIETLANY SPIS TREŚCI
OSTATNIO WYŚWIETLANY SPIS TREŚCI

