Окружность и эллипс относятся к кривым второго порядка,

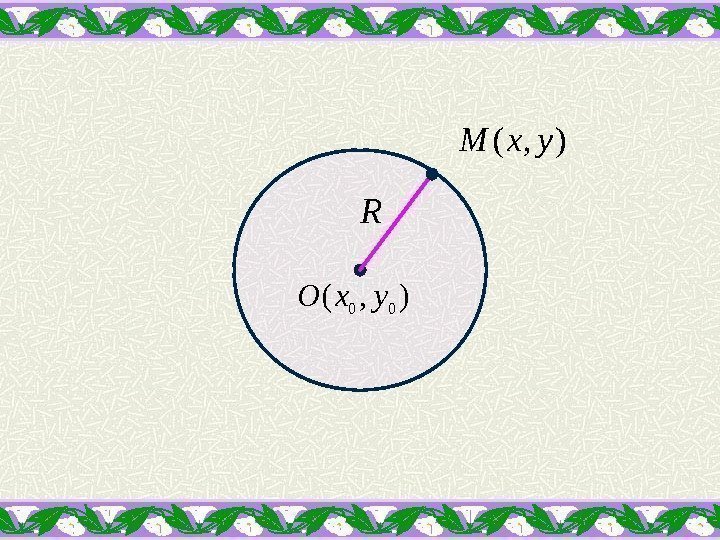
Окружность и эллипс относятся к кривым второго порядка, которые описываются уравнениями второй степени с двумя переменными. Выберем на окружности произвольную точку М(х, у). Пусть дана окружность радиуса R с центром в точке О(х 0 , у 0 ). Найдем ее уравнение.

), ( yx. M ), ( 00 yx. OR

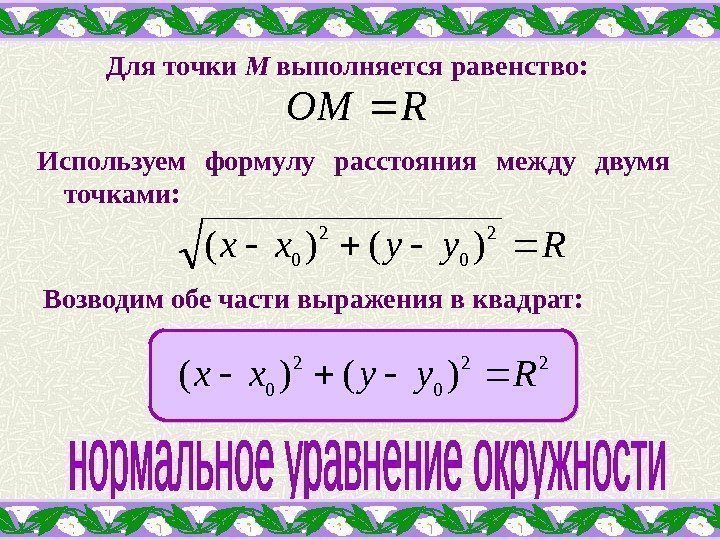
Для точки М выполняется равенство: ROM Используем формулу расстояния между двумя точками: Ryyxx 2 0)()( Возводим обе части выражения в квадрат: 22 0 2 0)()(Ryyxx

Если центр окружности лежит в начале координат (0, 0): 222 Ryx

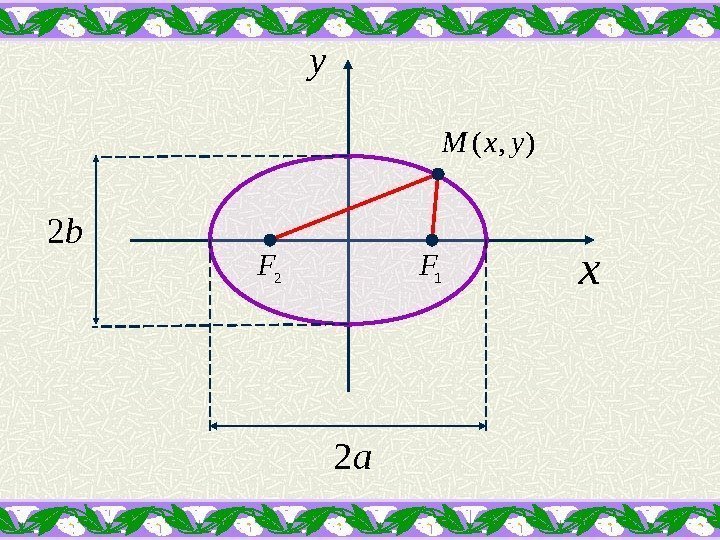
ЭЛЛИПСОМ называется множество точек плоскости, сумма расстояний от каждой до двух данных точек, называемых фокусами, есть величина постоянная.

x y ), (yx. M 1 F 2 F b 2 a

Введем обозначения: a – большая полуось эллипса b – малая полуось эллипса Для любой точки М(х, у), принадлежащей эллипсу, по определению выполняется равенство: )0; (21 c. FF 2 21 a. MFM

Для того, чтобы точка М(х, у) принадлежала эллипсу, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению1 2 2 b y a x где 222 cab

Покажем, что координаты точки, принадлежащей эллипсу, удовлетворяют уравнению (1). Т. к. точка М(х, у) принадлежит эллипсу, то по определению эллипса, должно выполнятся условие Выразим каждое расстояние по формуле расстояния между двумя точками: a. MFMF 221 )0; ( 1 c. F ); (yx. M 22 1 )(ycx. M

Тогда: )0; (2 c. F ); (yx. M 22 2)(ycx. MF aycxycx. MFMF 2)()( 2222 21 2222 )(2)(ycxaycx

2222222 )()(44)(ycxycxaaycx. Возводим в квадрат обе части выражения: 2222222 2)(442 ccxxycxaaccxx cxaycxa 222 )(

Возводим в еще раз квадрат: 22242222222 22 xccxaayacaxcaxa 224222222 caayaxcxa )()( 2222 caayacax 2 b 2 b Делим все выражение на 22 ba

1 2 2 22 b y a x

Отношение фокусного расстояния к длине большой оси эллипса называется ЭКСЦЕНТРИСИТЕТОМ a c

Для эллипса Следовательно, для эллипса Чем меньше отношение малой и большой полуосей, тем больше эксцентриситет и тем более вытянутым будет эллипс вдоль оси х, и наоборот. Приac 22 22 2 1 a ba a c 10 0 ab имеем окружность.

Пусть дан эллипс: Это уравнение эквивалентно системе двух параметрических уравнений: Проверим: 1 2 2 22 b y a x tby tax sin cos tby tax 222 sin cos 1 sincos 22 2 22 tt b tb a ta

tby tax sin cos