Модуль 2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Плоскость и её















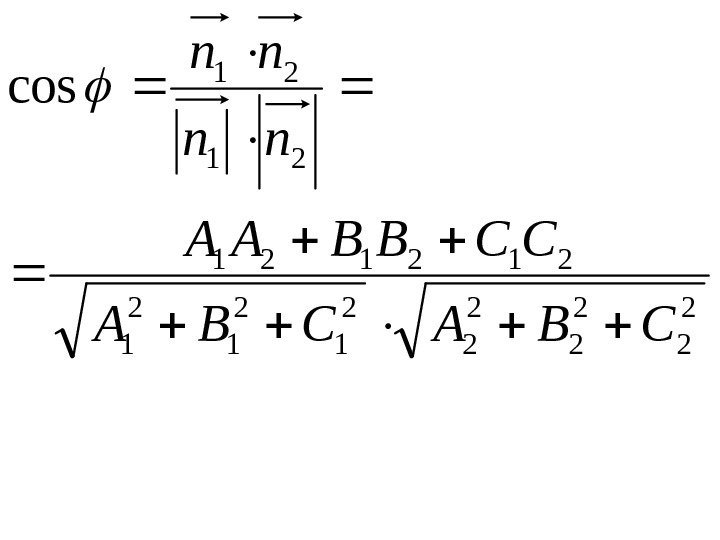
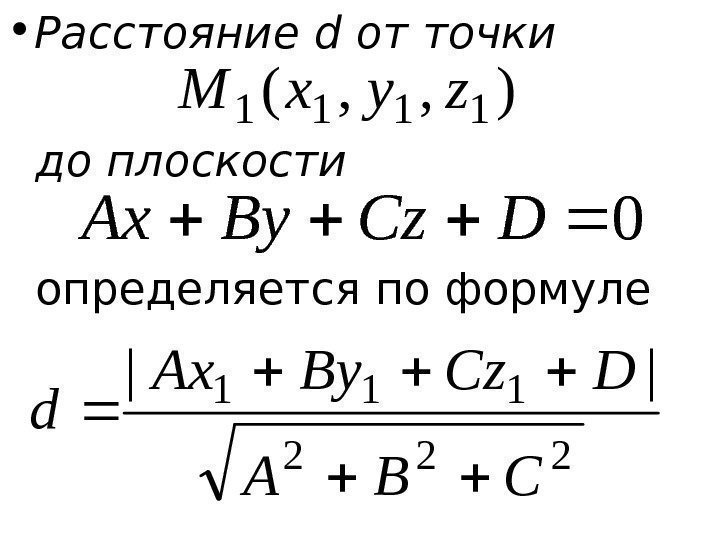









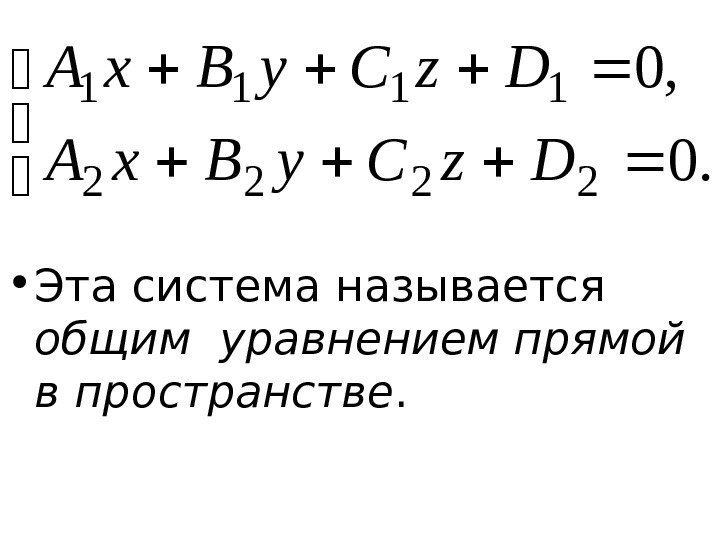









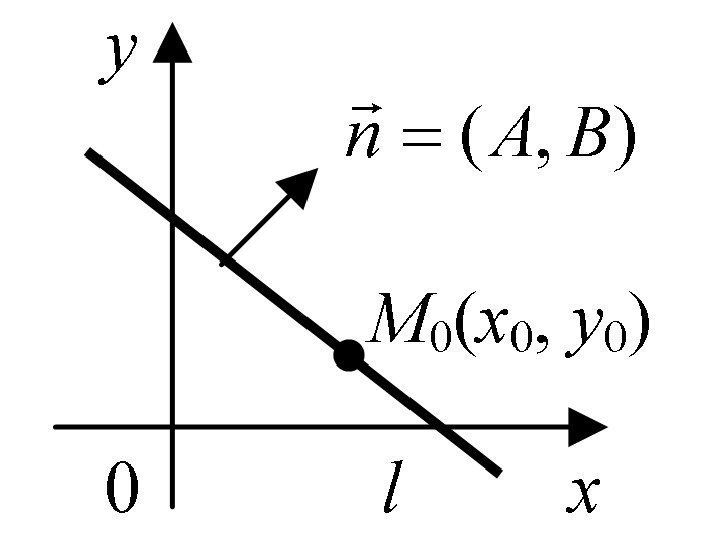

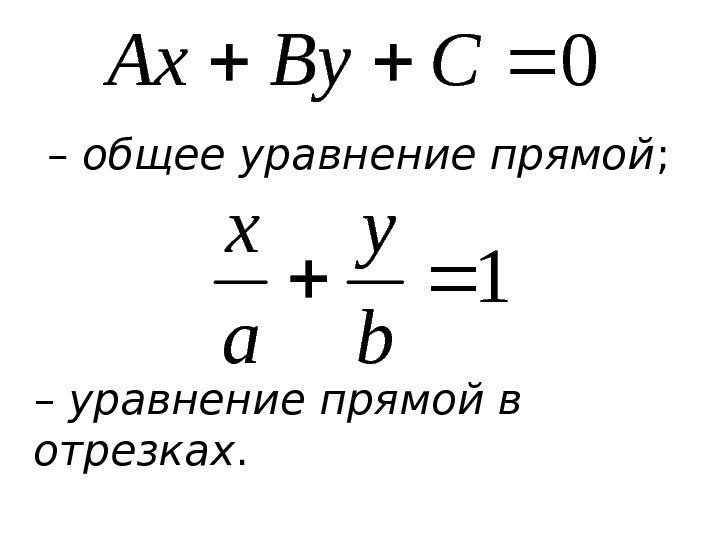

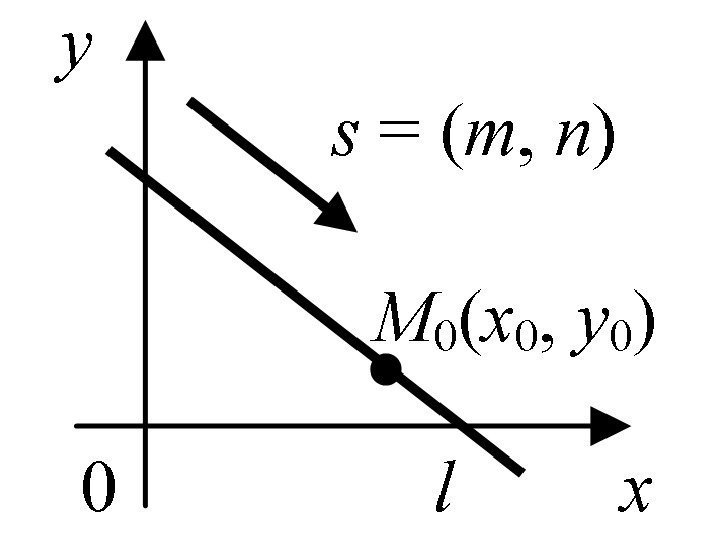

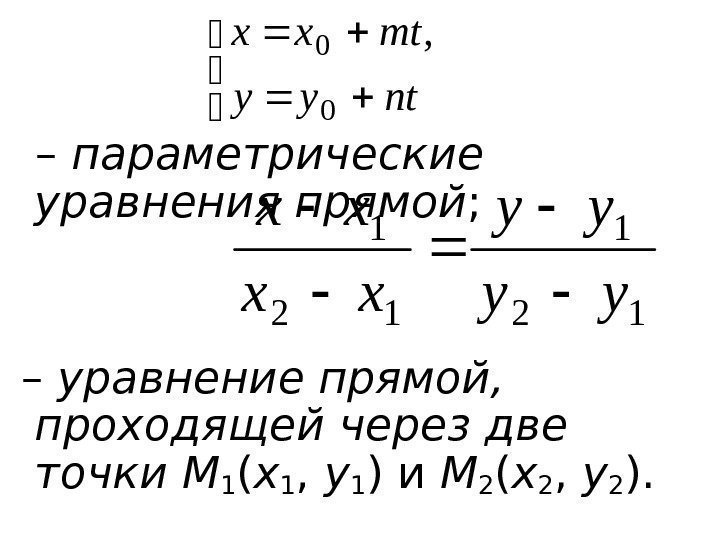

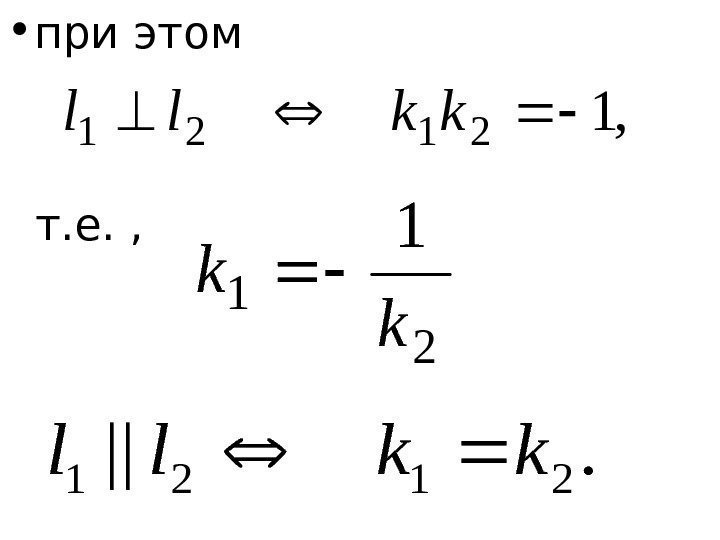




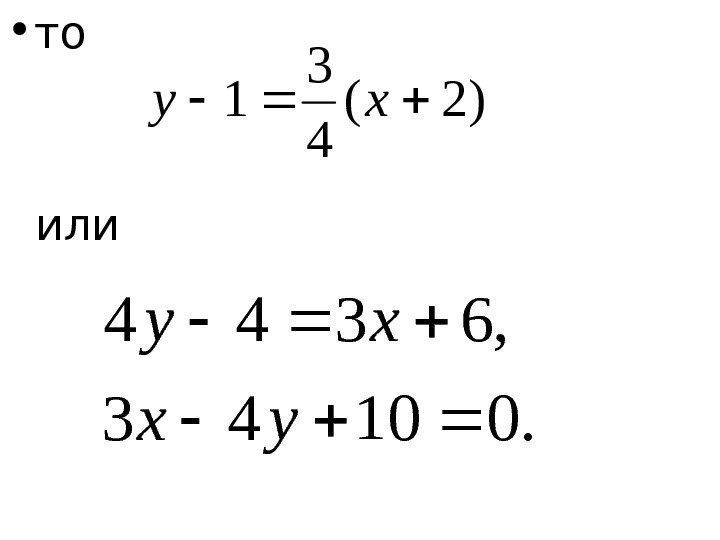

analit_geo_1.ppt
- Размер: 267.5 Кб
- Автор:
- Количество слайдов: 60
Описание презентации Модуль 2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Плоскость и её по слайдам
 Модуль 2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Модуль 2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
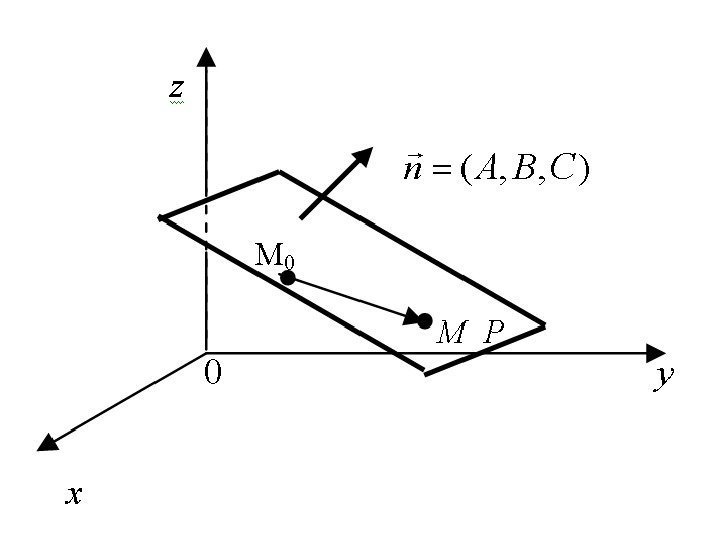
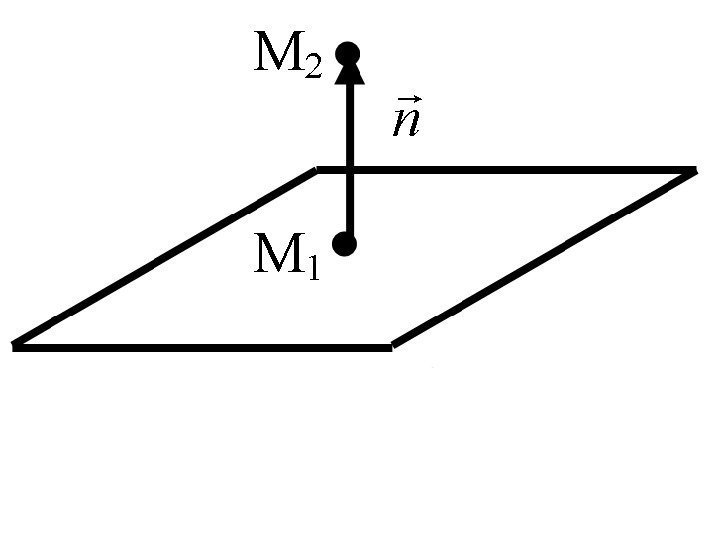
 Плоскость и её основные уравнения • Рассмотрим плоскость P в прямоугольной декартовой системе координат.
Плоскость и её основные уравнения • Рассмотрим плоскость P в прямоугольной декартовой системе координат.
 • Положение плоскости вполне определяется точкой и вектором нормали. Pzyx. M), , ( 0000 )0(), , ( n. PCBAn
• Положение плоскости вполне определяется точкой и вектором нормали. Pzyx. M), , ( 0000 )0(), , ( n. PCBAn

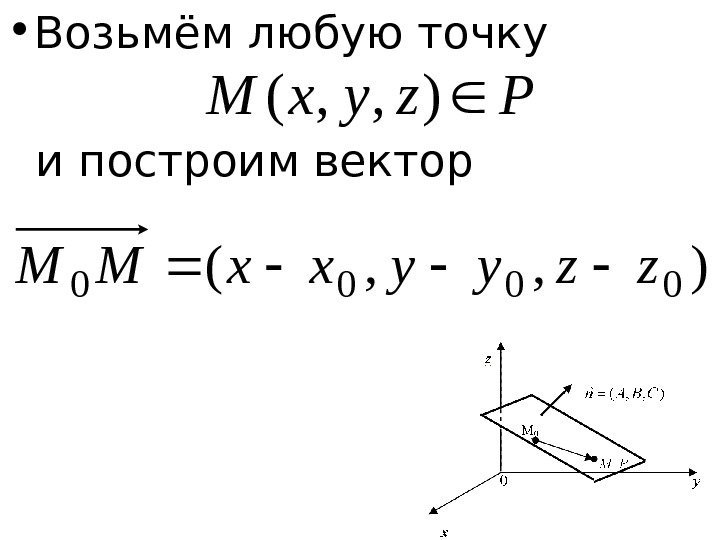
 • Возьмём любую точку и построим вектор Pzyx. M), , ( 0000 zzyyxx. MM
• Возьмём любую точку и построим вектор Pzyx. M), , ( 0000 zzyyxx. MM
 • Так как , то скалярное произведение или. MMn 0 , 0 0 MMn . 0)()()( 000 zz. Cyy. Bxx.
• Так как , то скалярное произведение или. MMn 0 , 0 0 MMn . 0)()()( 000 zz. Cyy. Bxx.
 • Получили уравнение плоскости , заданной точкой и вектором нормали ), , ( 0000 zyx. M ), , (CBAn
• Получили уравнение плоскости , заданной точкой и вектором нормали ), , ( 0000 zyx. M ), , (CBAn
 • Если в уравнении раскрыть скобки и обозначить то получим общее уравнение плоскости : 000 Cz. By. Ax. D 0)()()( 000 zz. Cyy. Bxx. A )0( 0 222 CBA DCz. By. Ax
• Если в уравнении раскрыть скобки и обозначить то получим общее уравнение плоскости : 000 Cz. By. Ax. D 0)()()( 000 zz. Cyy. Bxx. A )0( 0 222 CBA DCz. By. Ax
 • Теорема. Всякое уравнение вида определяет некоторую плоскость в пространстве. )0( 0 222 CBA DCz. By. Ax
• Теорема. Всякое уравнение вида определяет некоторую плоскость в пространстве. )0( 0 222 CBA DCz. By. Ax
 • Если в этом уравнении какой-либо из коэффициентов A, B, C равен нулю, то плоскость расположена параллельно той оси, координата которой отсутствует в уравнении.
• Если в этом уравнении какой-либо из коэффициентов A, B, C равен нулю, то плоскость расположена параллельно той оси, координата которой отсутствует в уравнении.
 • Например, при A = 0 плоскость By + Cz + D = 0 параллельна оси Ox ; при A = B = 0 плоскость Cz + D = 0 параллельна осям Ox и Oy , т. е. плоскости x. Oy и т. д.
• Например, при A = 0 плоскость By + Cz + D = 0 параллельна оси Ox ; при A = B = 0 плоскость Cz + D = 0 параллельна осям Ox и Oy , т. е. плоскости x. Oy и т. д.
 • Пусть в уравнении ни один из коэффициентов не равен 0. Перепишем это уравнение в виде разделим обе части этого равенства на — D и обозначим 0 DCz. By. Ax
• Пусть в уравнении ни один из коэффициентов не равен 0. Перепишем это уравнение в виде разделим обе части этого равенства на — D и обозначим 0 DCz. By. Ax
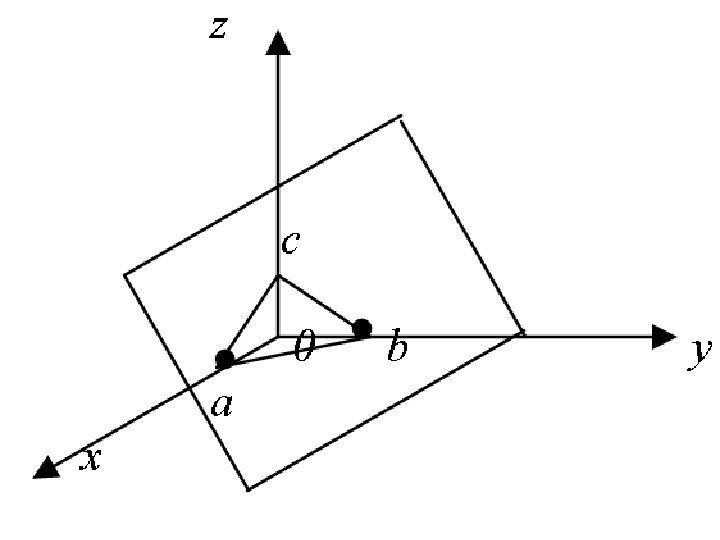
 Получим уравнение плоскости в отрезках : c C D b B D a A D , , , 1 c z b y a x
Получим уравнение плоскости в отрезках : c C D b B D a A D , , , 1 c z b y a x
 • где a, b, c – это величины направленных отрезков, отсекаемых плоскостью на осях координат
• где a, b, c – это величины направленных отрезков, отсекаемых плоскостью на осях координат

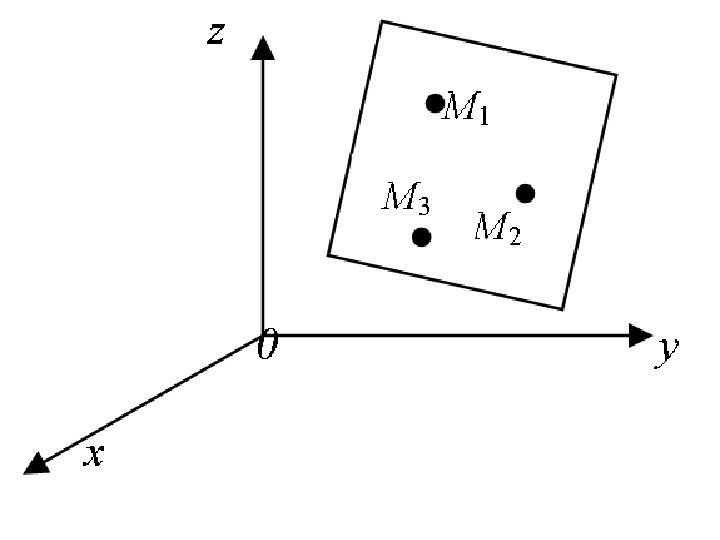
 • Если три точки не лежат на одной прямой, то через эти точки проходит единственная плоскость : ), , ( 1111 zyx. M ), , ( 2222 zyx. M ), , ( 3333 zyx. M
• Если три точки не лежат на одной прямой, то через эти точки проходит единственная плоскость : ), , ( 1111 zyx. M ), , ( 2222 zyx. M ), , ( 3333 zyx. M

 • Уравнение плоскости, проходящей через три точки , имеет вид: . 0 131313 121212 111 zzyyxx
• Уравнение плоскости, проходящей через три точки , имеет вид: . 0 131313 121212 111 zzyyxx
 • Пусть даны две плоскости и • Угол φ между двумя плоскостями равен углу между их векторами нормали: 0: 11111 Dz. Cy. Bx. AP 0: 22222 Dz. Cy. Bx. AP
• Пусть даны две плоскости и • Угол φ между двумя плоскостями равен углу между их векторами нормали: 0: 11111 Dz. Cy. Bx. AP 0: 22222 Dz. Cy. Bx. AP
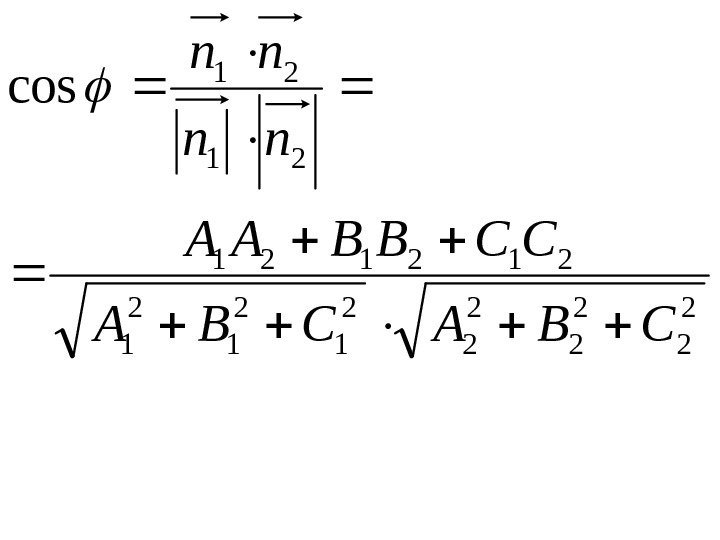 2 22 22 22 12 12 1 212121 21 21 cos CBACBA CCBBAA nn nn
2 22 22 22 12 12 1 212121 21 21 cos CBACBA CCBBAA nn nn
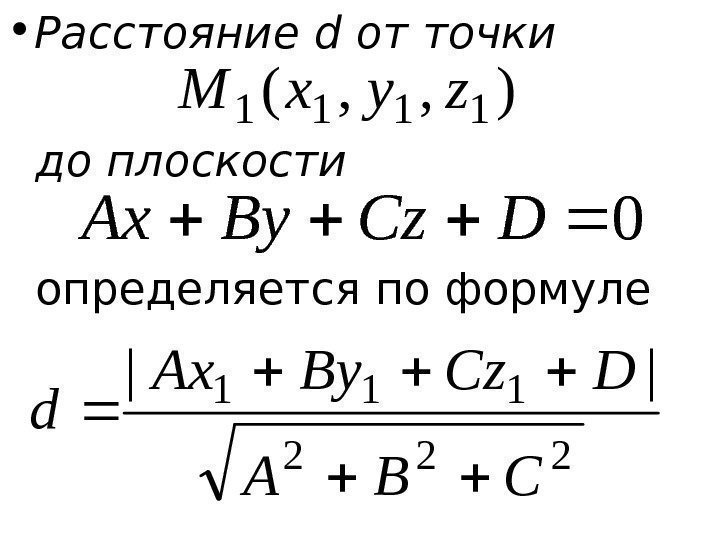 • Расстояние d от точки до плоскости определяется по формуле ), , ( 1111 zyx. M 0 DCz. By. Ax 222 111 || CBA DCz. By. Ax d
• Расстояние d от точки до плоскости определяется по формуле ), , ( 1111 zyx. M 0 DCz. By. Ax 222 111 || CBA DCz. By. Ax d
 • Пример. Даны две точки Записать уравнение плоскости, проходящей через точку M 1 перпендикулярно вектору )1, 0, 2( 1 M)2, 4, 1( 2 M. 21 MM
• Пример. Даны две точки Записать уравнение плоскости, проходящей через точку M 1 перпендикулярно вектору )1, 0, 2( 1 M)2, 4, 1( 2 M. 21 MM
 • Решение. Поскольку искомая плоскость перпендикулярна вектору , то в качестве вектора нормали возьмем вектор 21 MM )1, 4, 3( 21 MM n
• Решение. Поскольку искомая плоскость перпендикулярна вектору , то в качестве вектора нормали возьмем вектор 21 MM )1, 4, 3( 21 MM n

 • Подставив теперь в уравнение а также координаты точки M 1 : получим уравнение 0)()()( 000 zz. Cyy. Bxx. A 1, 4, 3 CBA 1, 0, 2 000 zyx
• Подставив теперь в уравнение а также координаты точки M 1 : получим уравнение 0)()()( 000 zz. Cyy. Bxx. A 1, 4, 3 CBA 1, 0, 2 000 zyx
 или – это и есть искомое общее уравнение плоскости 0)1(1)0(4)2(3 zyx 0543 zyx
или – это и есть искомое общее уравнение плоскости 0)1(1)0(4)2(3 zyx 0543 zyx
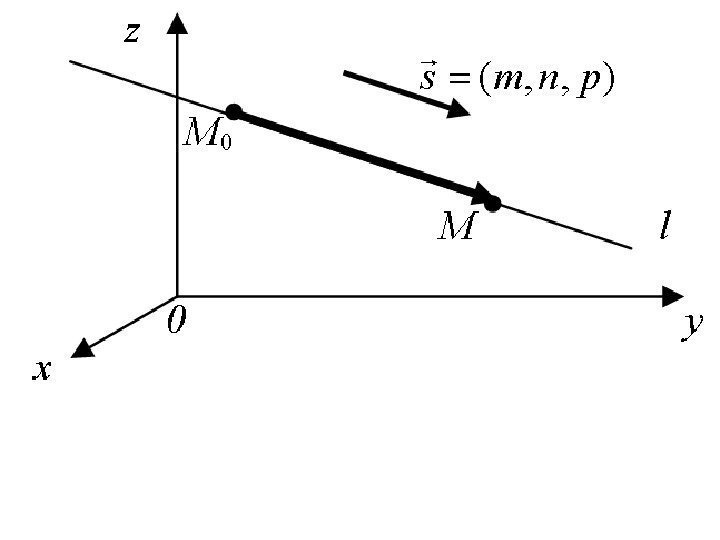
 Прямая в пространстве и её основные уравнения • Рассмотрим прямую l в прямоугольной декартовой системе координат. Положение прямой в пространстве вполне определяется точкой и направляющим вектором lzyx. M), , (0000 lpnms||), , (
Прямая в пространстве и её основные уравнения • Рассмотрим прямую l в прямоугольной декартовой системе координат. Положение прямой в пространстве вполне определяется точкой и направляющим вектором lzyx. M), , (0000 lpnms||), , (

 • Возьмем любую точку и построим вектор , из условия коллинеарности этих векторов получим канонические уравнения прямой в пространстве: lzyx. M), , ( s. MM || 0 p zz n yy m xx
• Возьмем любую точку и построим вектор , из условия коллинеарности этих векторов получим канонические уравнения прямой в пространстве: lzyx. M), , ( s. MM || 0 p zz n yy m xx
 • Обозначим коэффициент пропорциональности через параметр t и выразим через t переменные x, y, z. Приходим к параметрическим уравнениям прямой в пространстве : , , , 0 0 0 ptzz ntyy mtxx
• Обозначим коэффициент пропорциональности через параметр t и выразим через t переменные x, y, z. Приходим к параметрическим уравнениям прямой в пространстве : , , , 0 0 0 ptzz ntyy mtxx
 • Уравнение прямой, проходящей через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , имеет вид: . 12 1 zz zz yy yy xx xx
• Уравнение прямой, проходящей через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , имеет вид: . 12 1 zz zz yy yy xx xx
 • Рассмотрим две плоскости P 1 : A 1 x + B 1 y + C 1 z+ D 1 = 0 и P 2 : A 2 x + B 2 y + C 2 z+ D 2 = 0. Если эти плоскости не параллельны, то они пересекаются по прямой, задаваемой системой уравнений:
• Рассмотрим две плоскости P 1 : A 1 x + B 1 y + C 1 z+ D 1 = 0 и P 2 : A 2 x + B 2 y + C 2 z+ D 2 = 0. Если эти плоскости не параллельны, то они пересекаются по прямой, задаваемой системой уравнений:
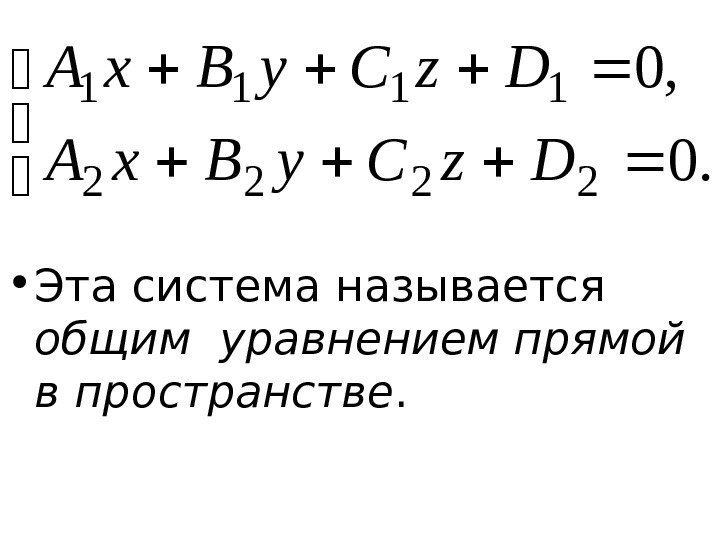 • Эта с истема называется общим уравнением прямой в пространстве. . 0 , 0 2222 1111 Dz. Cy. Bx.
• Эта с истема называется общим уравнением прямой в пространстве. . 0 , 0 2222 1111 Dz. Cy. Bx.
 • Угол φ между двумя прямыми l 1 и l 2 равен углу между их направляющими векторами и ), , ( 1111 pnms ), , ( 2222 pnms 2 2 2 2 1 2 1 212121 21 21 |||| cos pnmpnm ppnnmm ss ss
• Угол φ между двумя прямыми l 1 и l 2 равен углу между их направляющими векторами и ), , ( 1111 pnms ), , ( 2222 pnms 2 2 2 2 1 2 1 212121 21 21 |||| cos pnmpnm ppnnmm ss ss
 • Угол ψ между прямой и плоскостью Ax + By + Cz + D = 0 определяется по формуле p zz n yy m xx 000 222222 || sin pnm. CBA Cp. Bn. Am
• Угол ψ между прямой и плоскостью Ax + By + Cz + D = 0 определяется по формуле p zz n yy m xx 000 222222 || sin pnm. CBA Cp. Bn. Am
 • Пример. Составить канонические и параметрические уравнения прямой, проходящей через точки M 1 (3; 2; -1) и M 2 (4; 2; 1).
• Пример. Составить канонические и параметрические уравнения прямой, проходящей через точки M 1 (3; 2; -1) и M 2 (4; 2; 1).
 • Решение. Подставляем в формулу координаты точек M 1 (3; 2; -1) и M 2 (4; 2; 1) : 11 1 22 2 34 3 zyx
• Решение. Подставляем в формулу координаты точек M 1 (3; 2; -1) и M 2 (4; 2; 1) : 11 1 22 2 34 3 zyx
 • или – канонические уравнения прямой (нуль в знаменателе означает, что направляющий вектор перпендикулярен оси Oy , т. е. прямая перпендикулярна оси Oy ). 2 1 0 2 1 3 zyx )2, 0, 1(s
• или – канонические уравнения прямой (нуль в знаменателе означает, что направляющий вектор перпендикулярен оси Oy , т. е. прямая перпендикулярна оси Oy ). 2 1 0 2 1 3 zyx )2, 0, 1(s
 • Запишем параметрические уравнения прямой: t zyx 2 1 0 2 1 3 , 21, 02, 3 tzytx 21, 2,
• Запишем параметрические уравнения прямой: t zyx 2 1 0 2 1 3 , 21, 02, 3 tzytx 21, 2,
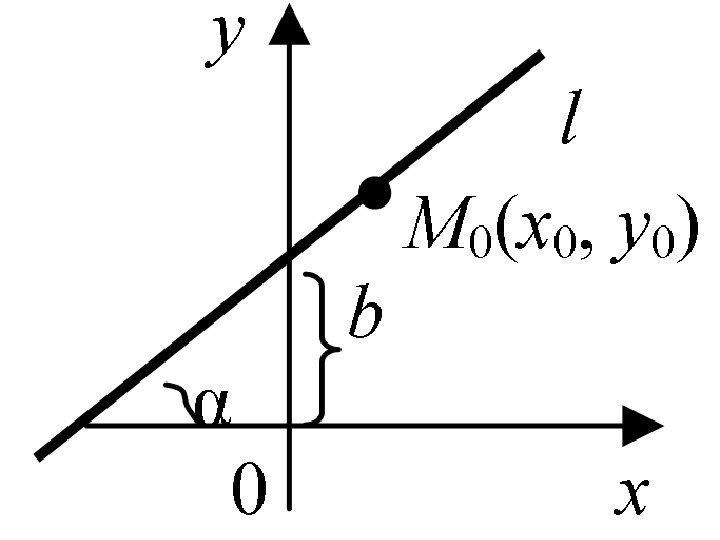
 Прямая на плоскости и её основные уравнения • Уравнение прямой с угловым коэффициентом k имеет вид или bkxy )( 00 xxkyy
Прямая на плоскости и её основные уравнения • Уравнение прямой с угловым коэффициентом k имеет вид или bkxy )( 00 xxkyy
 где k = tg α – угловой коэффициент прямой, b – величина отрезка, отсекаемого этой прямой на оси Oy , (x 0 , y 0 ) – точка, лежащая на прямой.
где k = tg α – угловой коэффициент прямой, b – величина отрезка, отсекаемого этой прямой на оси Oy , (x 0 , y 0 ) – точка, лежащая на прямой.

 • Кроме того, прямую l на плоскости можно задать вектором нормали и точкой l. BAn), ( lyx. M), (
• Кроме того, прямую l на плоскости можно задать вектором нормали и точкой l. BAn), ( lyx. M), (
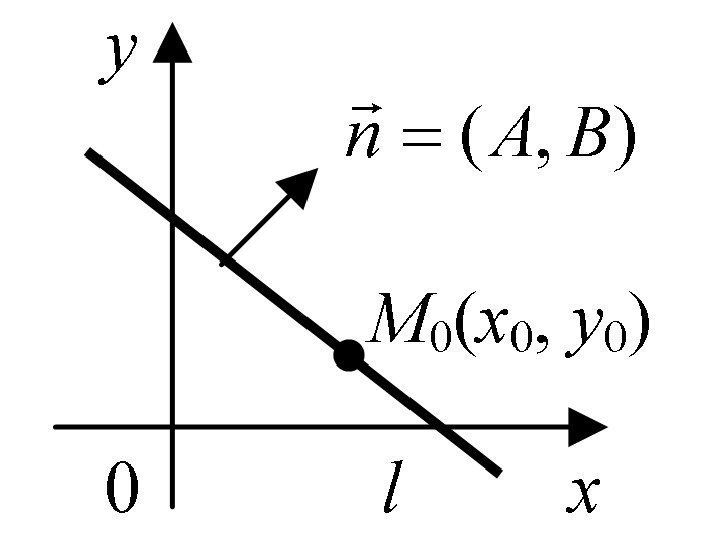
 • Получим три уравнения, аналогичные уравнениям для плоскости: – уравнение прямой , заданной точкой и вектором нормали ; 0)()( 00 yy. Bxx.
• Получим три уравнения, аналогичные уравнениям для плоскости: – уравнение прямой , заданной точкой и вектором нормали ; 0)()( 00 yy. Bxx.
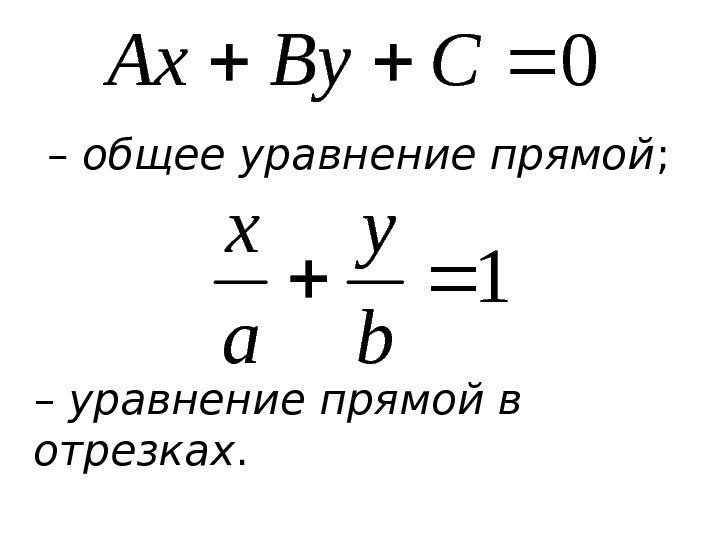 – общее уравнение прямой ; – уравнение прямой в отрезках. 0 CBy. Ax 1 b y a x
– общее уравнение прямой ; – уравнение прямой в отрезках. 0 CBy. Ax 1 b y a x
 • Прямая l на плоскости также определяется направляющим вектором и точкой lnms||), ( lyx. M), (
• Прямая l на плоскости также определяется направляющим вектором и точкой lnms||), ( lyx. M), (
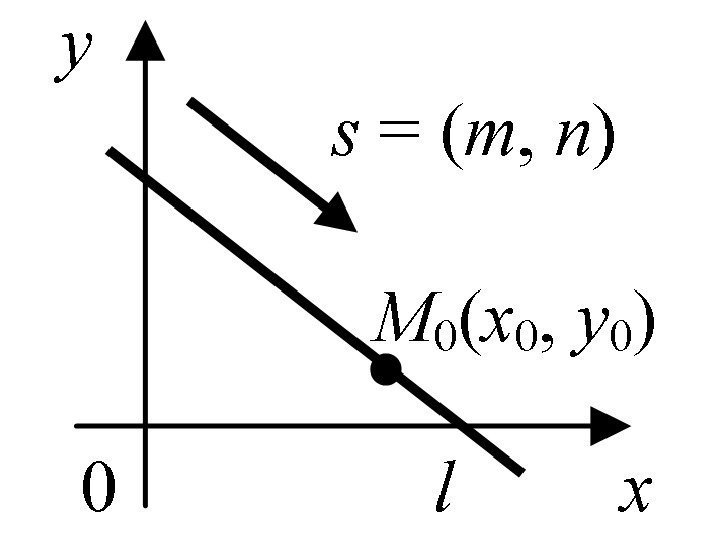
 • Получим еще 3 уравнения, аналогичные уравнениям прямой в пространстве: – каноническое уравнение прямой ; n yy m xx
• Получим еще 3 уравнения, аналогичные уравнениям прямой в пространстве: – каноническое уравнение прямой ; n yy m xx
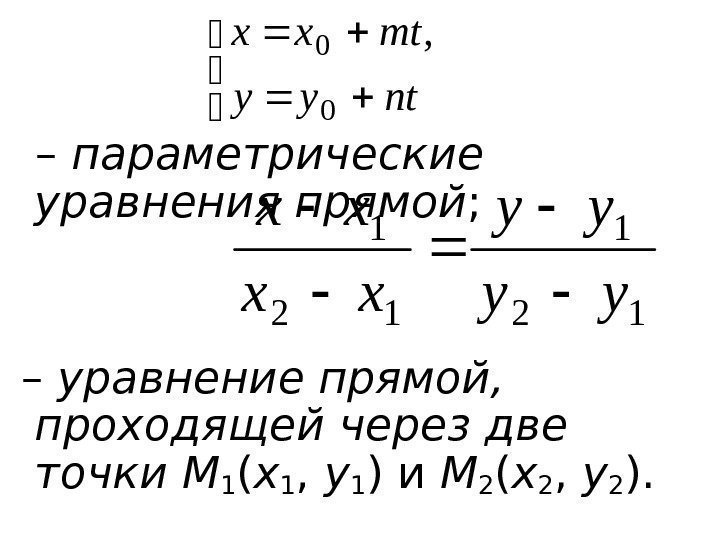 – параметрические уравнения прямой ; – уравнение прямой, проходящей через две точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ). ntyy mtxx 0 0 , 12 1 yy yy xx xx
– параметрические уравнения прямой ; – уравнение прямой, проходящей через две точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ). ntyy mtxx 0 0 , 12 1 yy yy xx xx
 • Угол между двумя прямыми , заданными уравнениями: l 1 : и l 2 : можно найти по формуле 11 bxky 22 bxky 21 12 1 kk kk tg
• Угол между двумя прямыми , заданными уравнениями: l 1 : и l 2 : можно найти по формуле 11 bxky 22 bxky 21 12 1 kk kk tg
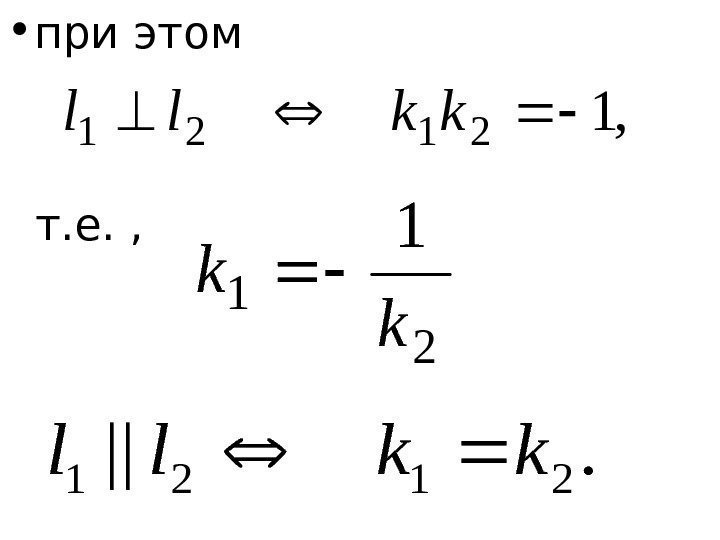 • при этом т. е. , , 1 2121 kkll 2 1 1 k k. || 2121 kkll
• при этом т. е. , , 1 2121 kkll 2 1 1 k k. || 2121 kkll
 • Расстояние d от точки M 1 ( x 1 , y 1 ) до прямой Ax + By + C = 0 вычисляется по формуле 22 11 || BA CBy. Ax d
• Расстояние d от точки M 1 ( x 1 , y 1 ) до прямой Ax + By + C = 0 вычисляется по формуле 22 11 || BA CBy. Ax d
 • Пример. Записать уравнения прямых, проходящих через точку M ( – 2, 1) параллельно и перпендикулярно прямой 3 x – 4 y + 12 = 0.
• Пример. Записать уравнения прямых, проходящих через точку M ( – 2, 1) параллельно и перпендикулярно прямой 3 x – 4 y + 12 = 0.
 • Решение. Перепишем общее уравнение прямой 3 x – 4 y + 12 = 0 , выразив из него переменную y : 3 4 3 : xyl
• Решение. Перепишем общее уравнение прямой 3 x – 4 y + 12 = 0 , выразив из него переменную y : 3 4 3 : xyl
 • Получили уравнение прямой с угловым коэффициентом k = 3/4. Запишем уравнение прямой и проходящей через точку M ( – 2, 1). Поскольку для параллельных прямых угловые коэффициенты равны, т. е. ll|| 1 4 3 1 kk
• Получили уравнение прямой с угловым коэффициентом k = 3/4. Запишем уравнение прямой и проходящей через точку M ( – 2, 1). Поскольку для параллельных прямых угловые коэффициенты равны, т. е. ll|| 1 4 3 1 kk
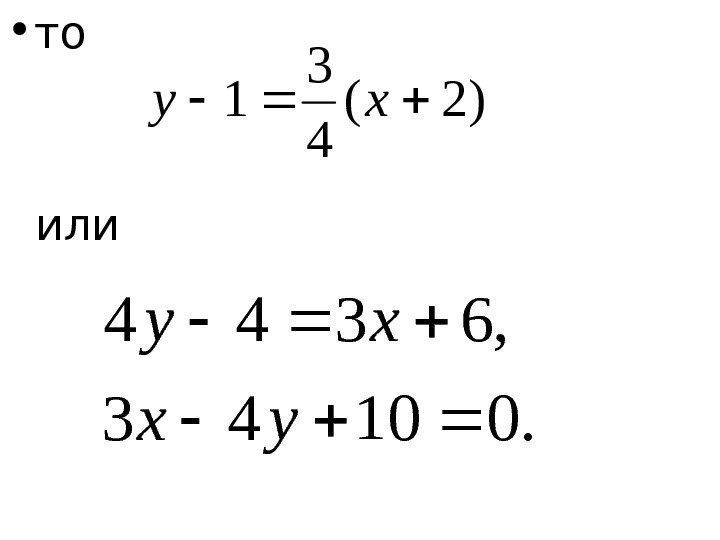 • то или )2( 4 3 1 xy. 01043 , 6344 yx xy
• то или )2( 4 3 1 xy. 01043 , 6344 yx xy
 • Составим уравнение прямой , проходящей через точку M ( – 2, 1). Так как угловые коэффициенты перпендикулярных прямых связаны соотношением тоll 2 3 41 2 k k
• Составим уравнение прямой , проходящей через точку M ( – 2, 1). Так как угловые коэффициенты перпендикулярных прямых связаны соотношением тоll 2 3 41 2 k k
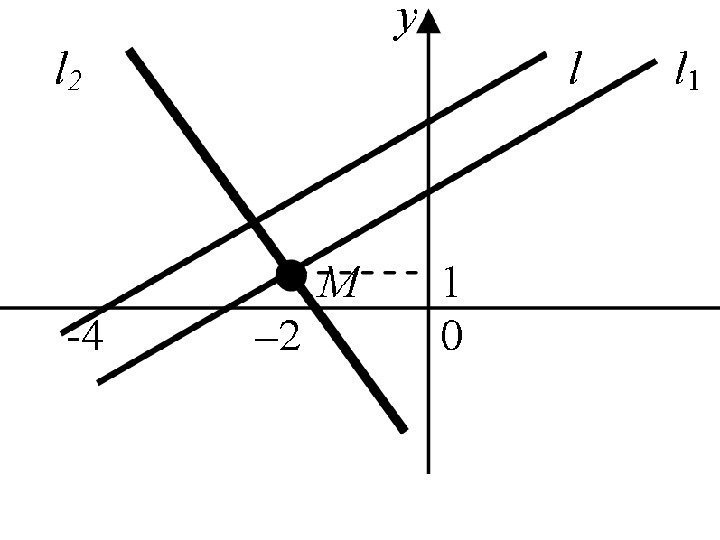
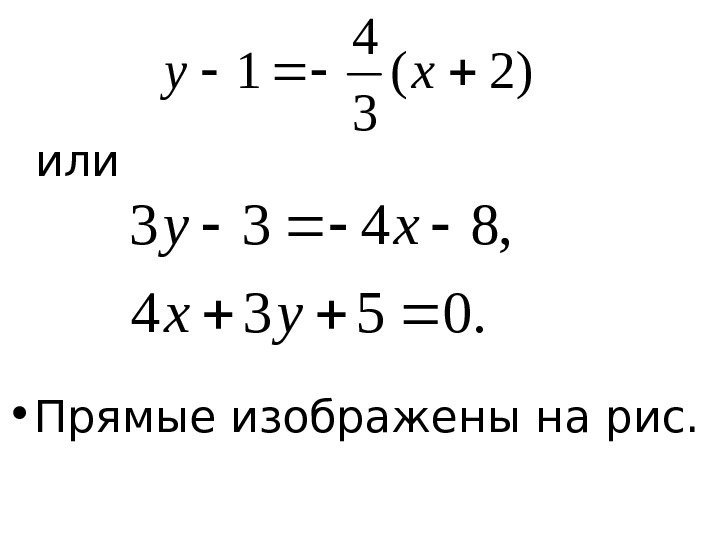 или • Прямые изображены на рис. )2( 3 4 1 xy. 0534 , 8433 yx xy
или • Прямые изображены на рис. )2( 3 4 1 xy. 0534 , 8433 yx xy

