Pr_MAT_L3 (3).ppt
- Количество слайдов: 15

Модель рівноважних цін Розглянемо балансову модель, яку називають моделлю рівноважних цін. Нехай задано матриці:

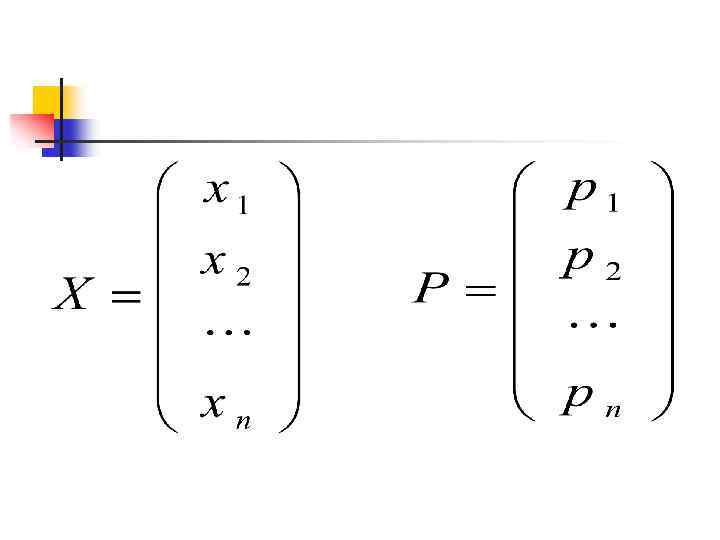

де А – матриця прямих витрат; Х – матриця обсягів валової продукції; Р – матриця цін, і-та координата якої дорівнює ціні одиниці продукції і-ої галузі.

n Тоді, наприклад і-та галузь одержить прибуток, який дорівнює р1 х1. Частину свого прибутку ця галузь витратить на закупівлю продукції інших галузей.

n Так, для випуску одиниці продукції їй необхідна продукція першої галузі в обсязі а 1 1 , другої галузі – в обсязі а 2 1, n-ої галузі – в обсязі аn 1.

На закупівлю цієї продукції буде витрачено суму, що становить a 1 1∙ p 1 + a 2 1∙ p 2 + …+ an 1∙ pn.

Отже, першій галузі для випуску продукції в обсязі х1 необхідно витратити на закупівлю продукції інших галузей суму, що становить x 1∙( a 1 1∙ p 1 + a 2 1∙ p 2 + …+ an 1∙ pn )

n Частину доходу, що залишилась, позначимо V 1 (ця частина доходу називається додатковою вартістю і йде на виплату заробітної плати і податків, підприємницький прибуток та інвестиції).

Таким чином, справджується рівність: x 1 p 1 = x 1∙( a 1 1∙ p 1 + a 2 1∙ p 2 + …+ an 1∙ pn )+ V 1.

Поділивши її на х1, дістанемо p 1 = ( a 1 1∙ p 1 + a 2 1∙ p 2 + …+ an 1∙ pn )+ W 1,

де W 1= V 1 / x 1 – норма додаткової вартості (тобто додаткова вартість на одиницю продукції, що випускається).

Аналогічно для інших галузей дістанемо P 2 = ( a 1 2 ∙ p 1 + a 2 2 ∙ p 2 + …+ an 2 ∙ pn )+ W 2 , ………………………………. ……. Pn = ( a 1 n ∙ p 1 + a 2 n ∙ p 2 + …+ an n ∙ pn )+ Wn.

Отримані рівності можна записати в матричній формі: P = A P + W, T∙ (9)

n n де AT – матриця, транспонована до матриці A; W – матриця-стовпець норм додаткової вартості.
Pr_MAT_L3 (3).ppt