МНОЖЕСТВО – совокупность объектов любой природы, объединенных по











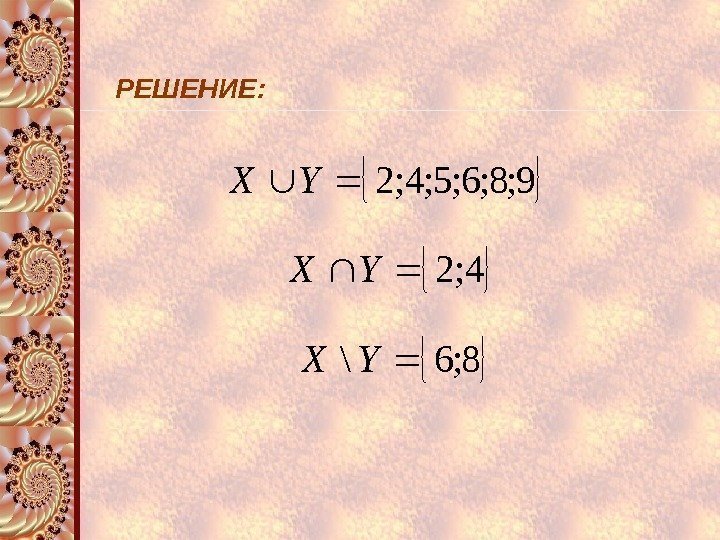


5.1...ppt
- Размер: 433.0 Кб
- Автор:
- Количество слайдов: 16
Описание презентации МНОЖЕСТВО – совокупность объектов любой природы, объединенных по по слайдам

 МНОЖЕСТВО – совокупность объектов любой природы, объединенных по какому-либо признаку. Объекты, составляющие множество, называются элементами этого множества. Обозначается: А – множество, а – элемент множества АAb. Aa,
МНОЖЕСТВО – совокупность объектов любой природы, объединенных по какому-либо признаку. Объекты, составляющие множество, называются элементами этого множества. Обозначается: А – множество, а – элемент множества АAb. Aa,
 ПРИМЕРЫ МНОЖЕСТВ : Множество студентов ВУЗа Множество рыб в аквариуме Множество судов на причале
ПРИМЕРЫ МНОЖЕСТВ : Множество студентов ВУЗа Множество рыб в аквариуме Множество судов на причале
 Пусть Х и У – два множества. Между ними возможны следующие отношения: Множество, не содержащее ни одного элемента, называется пустым 0. 1 Если оба множества состоят из одних и тех же элементов, то они совпадают. Х=У
Пусть Х и У – два множества. Между ними возможны следующие отношения: Множество, не содержащее ни одного элемента, называется пустым 0. 1 Если оба множества состоят из одних и тех же элементов, то они совпадают. Х=У
 2 Если все элементы множества Х содержатся в У, то Х является подмножеством У. YX
2 Если все элементы множества Х содержатся в У, то Х является подмножеством У. YX
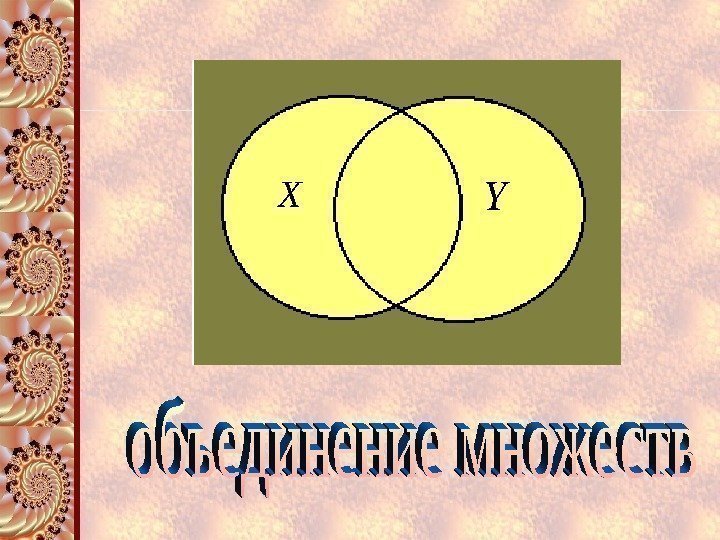
 3 ОБЪЕДИНЕНИЕМ двух множеств Х и У называется множество Z , состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. YXZ
3 ОБЪЕДИНЕНИЕМ двух множеств Х и У называется множество Z , состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. YXZ
 X Y
X Y
 4 ПЕРЕСЕЧЕНИЕМ двух множеств Х и У называется множество Z , состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств. YXZ
4 ПЕРЕСЕЧЕНИЕМ двух множеств Х и У называется множество Z , состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств. YXZ
 X Y
X Y
 5 РАЗНОСТЬЮ двух множеств Х и У называется множество Е, состоящее из всех элементов множества Х, которые не принадлежат множеству У. YXE\
5 РАЗНОСТЬЮ двух множеств Х и У называется множество Е, состоящее из всех элементов множества Х, которые не принадлежат множеству У. YXE\
 X Y
X Y
 ПРИМЕР. Даны множества Х= {2; 4; 6; 8} Y={2; 4; 5; 9} Найти пересечение, объединение и разность этих множеств.
ПРИМЕР. Даны множества Х= {2; 4; 6; 8} Y={2; 4; 5; 9} Найти пересечение, объединение и разность этих множеств.
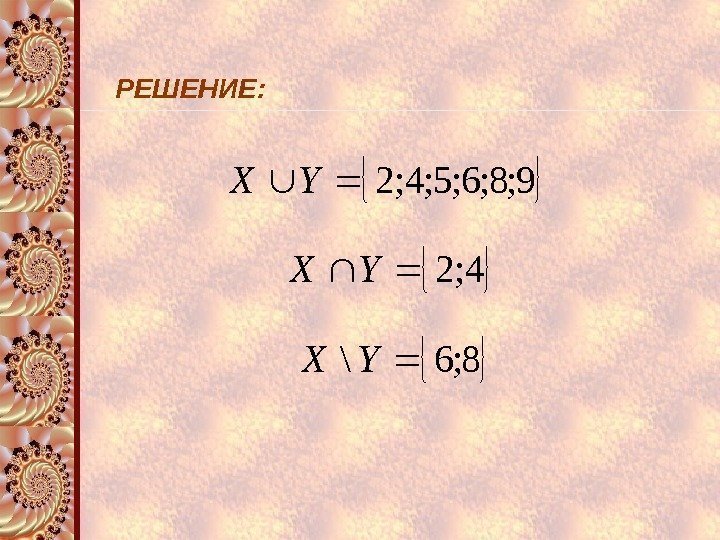 РЕШЕНИЕ: 9; 8; 6; 5; 4; 2 YX 8; 6\YX
РЕШЕНИЕ: 9; 8; 6; 5; 4; 2 YX 8; 6\YX
 Множества, элементами которых являются действительные числа, называются числовыми. R – множество действительных чисел Q – множество рациональных чисел I – множество иррациональных чисел Z – множество целых чисел N – множество натуральных чисел
Множества, элементами которых являются действительные числа, называются числовыми. R – множество действительных чисел Q – множество рациональных чисел I – множество иррациональных чисел Z – множество целых чисел N – множество натуральных чисел
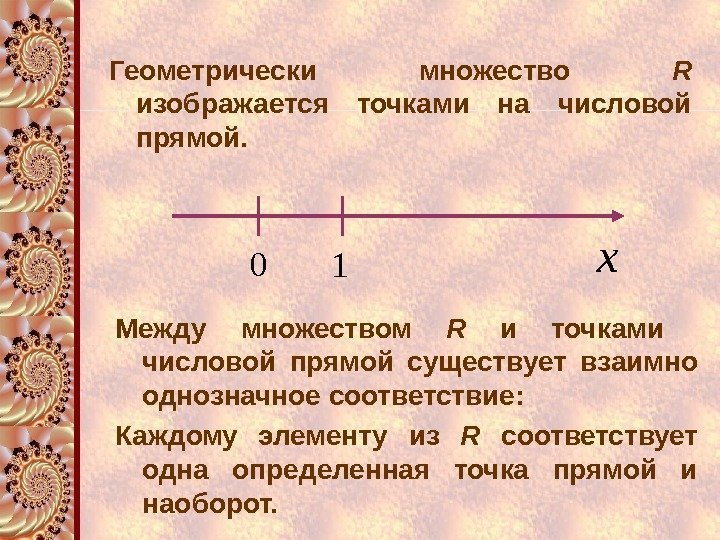
 Геометрически множество R изображается точками на числовой прямой. 01 x Между множеством R и точками числовой прямой существует взаимно однозначное соответствие: Каждому элементу из R соответствует одна определенная точка прямой и наоборот.
Геометрически множество R изображается точками на числовой прямой. 01 x Между множеством R и точками числовой прямой существует взаимно однозначное соответствие: Каждому элементу из R соответствует одна определенная точка прямой и наоборот.
 Множество Х, элементы которого удовлетворяют неравенствуbxa abназывается отрезком Множество Х, элементы которого удовлетворяют неравенству bxa называется интервалом ab Множество Х, элементы которого удовлетворяют одному из неравенств bxabxa называется полуинтервалом )[](abab
Множество Х, элементы которого удовлетворяют неравенствуbxa abназывается отрезком Множество Х, элементы которого удовлетворяют неравенству bxa называется интервалом ab Множество Х, элементы которого удовлетворяют одному из неравенств bxabxa называется полуинтервалом )[](abab
