Множества теория Новиков - копия.ppt
- Количество слайдов: 10
 Множества
Множества
 Элементы и множества Понятия множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимые друг от друга. Пример Множество S страниц в данной книге. Множество N натуральных чисел 1, 2, 3, … Множество Р простых чисел 2, 3, 5, 7, 11, … Множество Z целых чисел: … , -2, -1, 0, 1, 2, … Множество R вещественных чисел. Множество А различных символов на этой странице. Если объект х является элементом множества М, то говорят, что х принадлежит М. Обозначение: х М. В противном случае говорят, что х не принадлежит М. Обозначение: х М. Множество, не содержащее элементов, называется пустым. Обозначение Ø. Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсумом).
Элементы и множества Понятия множества принадлежит к числу фундаментальных неопределяемых понятий математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимые друг от друга. Пример Множество S страниц в данной книге. Множество N натуральных чисел 1, 2, 3, … Множество Р простых чисел 2, 3, 5, 7, 11, … Множество Z целых чисел: … , -2, -1, 0, 1, 2, … Множество R вещественных чисел. Множество А различных символов на этой странице. Если объект х является элементом множества М, то говорят, что х принадлежит М. Обозначение: х М. В противном случае говорят, что х не принадлежит М. Обозначение: х М. Множество, не содержащее элементов, называется пустым. Обозначение Ø. Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсумом).
 Задание множеств Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различным способами: • перечислением элементов: M : = {a 1, a 2, …, ak}; • характеристическим предикатом: M : = {x │P(x)}; • порождающей процедурой: M : = {x│x : = f}. ЗАМЕЧАНИЕ При задании множеств перечислением обозначения элементов обычно заключают в фигурные скобки и разделяют запятыми. Характеристический предикат – это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае – не принадлежит. Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества.
Задание множеств Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различным способами: • перечислением элементов: M : = {a 1, a 2, …, ak}; • характеристическим предикатом: M : = {x │P(x)}; • порождающей процедурой: M : = {x│x : = f}. ЗАМЕЧАНИЕ При задании множеств перечислением обозначения элементов обычно заключают в фигурные скобки и разделяют запятыми. Характеристический предикат – это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае – не принадлежит. Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества.
 Пример Замечание Множество целых чисел в диапазоне от m до n обозначают так: m. . n. То есть Перечислением можно задавать только конечные множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.
Пример Замечание Множество целых чисел в диапазоне от m до n обозначают так: m. . n. То есть Перечислением можно задавать только конечные множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.
 ОПЕРАЦИИ НАД МНОЖЕСТВАМИ Сравнение множеств Множество A содержится в множестве В ( множество В включает множество A ), если каждый элемент А есть элемент В: В этом случае А называется подмножеством В, В – надмножеством А. Если , то А называется собственным подмножеством В. Заметим, что . По определению . Замечание Если требуется различать собственные и несобственные подмножества, то для обозначения включения собственных подмножеств используется знак , а для несобственных - . • Равенство Два множества равны, если они являются подмножествами друга: Мощность множества M обозначается как |M|. Для конечных множеств мощность – это число элементов. Например, , но . Если |A| = |B|, то множества A и B называются равномощными.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ Сравнение множеств Множество A содержится в множестве В ( множество В включает множество A ), если каждый элемент А есть элемент В: В этом случае А называется подмножеством В, В – надмножеством А. Если , то А называется собственным подмножеством В. Заметим, что . По определению . Замечание Если требуется различать собственные и несобственные подмножества, то для обозначения включения собственных подмножеств используется знак , а для несобственных - . • Равенство Два множества равны, если они являются подмножествами друга: Мощность множества M обозначается как |M|. Для конечных множеств мощность – это число элементов. Например, , но . Если |A| = |B|, то множества A и B называются равномощными.
 Операции над множествами Обычно рассматриваются следующие операции над множествами:
Операции над множествами Обычно рассматриваются следующие операции над множествами:
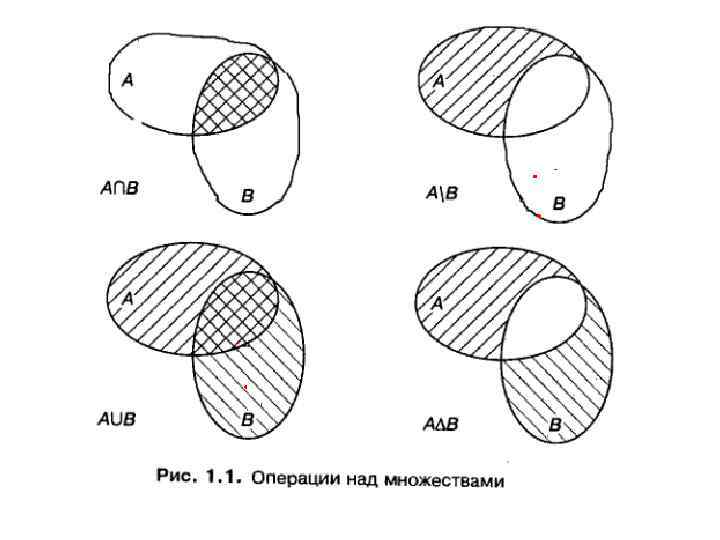
 Операция дополнения подразумевает некоторый универсум U : Ᾱ = U A. Пример Пусть A : = {1, 2, 3}, B : = {3, 4, 5}. Тогда A B = {1, 2, 3, 4, 5}, A B = {3}, A B = {1, 2}, A Δ B = {1, 2, 4, 5} На рис. 1. 1 приведены диаграммы Эйлера, иллюстрирующие операции над множествами. Сами исходные множества изображаются фигурами (в данном случае – овалом), а результат графически выделяется (в данном случае для выделения использована штриховка). Операции пересечения и объединения допускают следующее обобщение. Пусть I – некоторое множество, элементы которого используются как индексы, и пусть для любого і І множество Аі, известно. Тогда
Операция дополнения подразумевает некоторый универсум U : Ᾱ = U A. Пример Пусть A : = {1, 2, 3}, B : = {3, 4, 5}. Тогда A B = {1, 2, 3, 4, 5}, A B = {3}, A B = {1, 2}, A Δ B = {1, 2, 4, 5} На рис. 1. 1 приведены диаграммы Эйлера, иллюстрирующие операции над множествами. Сами исходные множества изображаются фигурами (в данном случае – овалом), а результат графически выделяется (в данном случае для выделения использована штриховка). Операции пересечения и объединения допускают следующее обобщение. Пусть I – некоторое множество, элементы которого используются как индексы, и пусть для любого і І множество Аі, известно. Тогда
 Свойства операций над множествами Пусть задан универсум U. Тогда выполняются следующие свойства:
Свойства операций над множествами Пусть задан универсум U. Тогда выполняются следующие свойства:

