Министерство образования Нижегородской области Государственное бюджетное образовательное учреждение

Министерство образования Нижегородской области Государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный инженерно-экономический университет» (ГБОУ ВО НГИЭУ) Дисциплина «Прикладная математика»

• Целью освоения учебной дисциплины «Прикладная математика» является приобретение знаний и умений, позволяющих в дальнейшем заниматься научной и прикладной деятельностью. При изучении этой дисциплины формируются общекультурные, общепрофессиональные и профессиональные компетенции. • Для решения этой цели предполагается решить следующие задачи: познакомить обучающихся с основными понятиями рядов Фурье и их прикладным значением; рассмотреть численные методы математики для решения задач. • В результате освоения дисциплины обучающийся должен: • знать: основные методы приближения функций с помощью рядов Фурье, основы численных методов для решения прикладных задач; • уметь: использовать в познавательной профессиональной деятельности базовые знания о рядах Фурье и численных методах; использовать математический аппарат и методы для обработки информации анализа данных; • владеть: методами приближения функций с помощью рядов Фурье, численными методами решения прикладных задач.

Формируемые компетенции Индекс (код) компетенции Название компетенции Общекультурные компетенции ОК-1 способностью к абстрактному мышлению, анализу, синтезу Общепрофессиональные компетенции ОПК-4 способностью использовать законы и методы математики, естественных, гуманитарных и экономических наук при решении стандартных и нестандартных профессиональных задач ПК-4 способностью и готовностью применять знания о современных методах исследований

Оценка Неудовлетворительно Удовлетворительно Хорошо Отлично Набранная сумма баллов ≤ 50 51 -70 71 -85 86 -100 Успеваемость студента по курсу «Прикладная математика» определяется с помощью традиционной 5 -балльной и 100 -балльной шкалы оценок. Форма итогового контроля дисциплины – экзамен

ОТЧЕТНОСТЬ • 1. КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «РЯДЫ ФУРЬЕ» – 20 БАЛЛОВ • 2. ТЕОРЕТИКО-ПРАКТИЧЕСКИЕ РАБОТЫ : • 2. 1. «Приближенное решение нелинейных уравнений» — 10 БАЛЛОВ • 2. 2. «Интерполирование табличных функций» — 10 БАЛЛОВ • 2. 3. «Численное решение обыкновенных дифференциальных уравнений» » — 10 БАЛЛОВ • 3. ДОКЛАД — 10 БАЛЛОВ (Применение рядов Фурье) • 4. РАБОТА НА ЗАНЯТИЯХ (Опрос – 1(б)*3=3 б , разбор конкретных ситуаций – 3(б)*2=6 б , кейс-технологий – 3 б) – 12 БАЛЛОВ • 5. ТЕСТИРОВАНИЕ – 20 БАЛЛОВ

Дисциплина «Прикладная математика» Модуль 1 «Ряды Фурье» Модуль 2 «Ч исленные методы » зач. ед час. Общая трудоемкость дисциплины по учебному плану 3 108 Аудиторные занятия (всего) 1 36 В том числе: Лекции (Л) — — Практические занятия (ПЗ) 1 36 Самостоятельная работа (всего) 1, 25 45 Вид контроля экзамен 0, 75 27 Распределение трудоемкости дисциплины по видам работ по семестрам для очной формы обучения

Основная литература 1. Бахвалов Н. С. Численные методы [Электронный ресурс]/ Бахвалов Н. С. , Жидков Н. П. , Кобельков Г. М. — Электрон. текстовые данные. — М. : БИНОМ. Лаборатория знаний, 2012. — 635 c. — Режим доступа: http: //www. iprbookshop. ru/6502. — ЭБС «IPRbooks» , по паролю 2. Черненко В. Д. Высшая математика в примерах и задачах. Том 2 [Электронный ресурс]: учебное пособие/ Черненко В. Д. — Электрон. текстовые данные. — СПб. : Политехника, 2011. — 568 c. — Режим доступа: http: //www. iprbookshop. ru/15891. — ЭБС «IPRbooks» , по паролю http: //www. iprbookshop. ru/15891. html Дополнительная литература 1. Численные методы: теория и практика: учеб. пособие для бакалавров / У. Г. Пирумов [и др. ]. – 5 -у изд. , перераб. и доп. – М. : Издательство Юрайт, 2012. – 421 с. – Серия : Бакалавр. Базовый курс. 2. Черненко В. Д. Высшая математика в примерах и задачах. Том 1 [Электронный ресурс]: учебное пособие/ Черненко В. Д. — Электрон. текстовые данные. — СПб. : Политехника, 2011. — 709 c. — Режим доступа: http: //www. iprbookshop. ru/15890. — ЭБС «IPRbooks» , по паролю 3. Черненко В. Д. Высшая математика в примерах и задачах. Том 3 [Электронный ресурс]: учебное пособие/ Черненко В. Д. — Электрон. текстовые данные. — СПб. : Политехника, 2011. — 507 c. — Режим доступа: http: //www. iprbookshop. ru/15892. — ЭБС «IPRbooks» , по паролю 4. Салимов Р. Б. Математика для инженеров и технологов [Электронный ресурс]: учебное пособие/ Салимов Р. Б. — Электрон. текстовые данные. — М. : ФИЗМАТЛИТ, 2009. — 484 c. — Режим доступа: http: //www. iprbookshop. ru/12917. — ЭБС «IPRbooks» , по паролю 5. Численные методы: учебник и практикум для академического бакалавриата / У. Г. Пирумов [и др. ]. ; под ред. У. Г. Пирумова. – 5 -е изд. , перераб. и доп. – М. : Издательство Юрайт, 2016. – • 1. Письменный Д. Т. Конспект лекций по высшей математике. М. Айрис Пресс, 2004. • 2. Лунгу К. Н. , Норин В. П. , Письменный Д. Т. , Шевченко Ю. А. Сборник задач по высшей математике. М. Айрис Пресс, 2004. • 3. Сборник индивидуальных заданий по высшей математике. ч. 3 (под редакцией А. П. Рябушко). Минск, «Высшая школа» , 1991.

Ряды Фурье Примерно с середины 18 века ученые были вовлечены в дискуссию по поводу возможности представления «произвольной» 2π-периодической функции в виде суммы тригонометрического ряда. В начале 19 века работы французского математика Ж. Б. Фурье открыли новую эпоху в теории тригонометрических рядов. Фурье смог представить в виде суммы тригонометрического ряда любую функцию. В его книге «Аналитическая теория тепла» , вышедшей в 1822 году, содержится много частных примеров таких представлений.

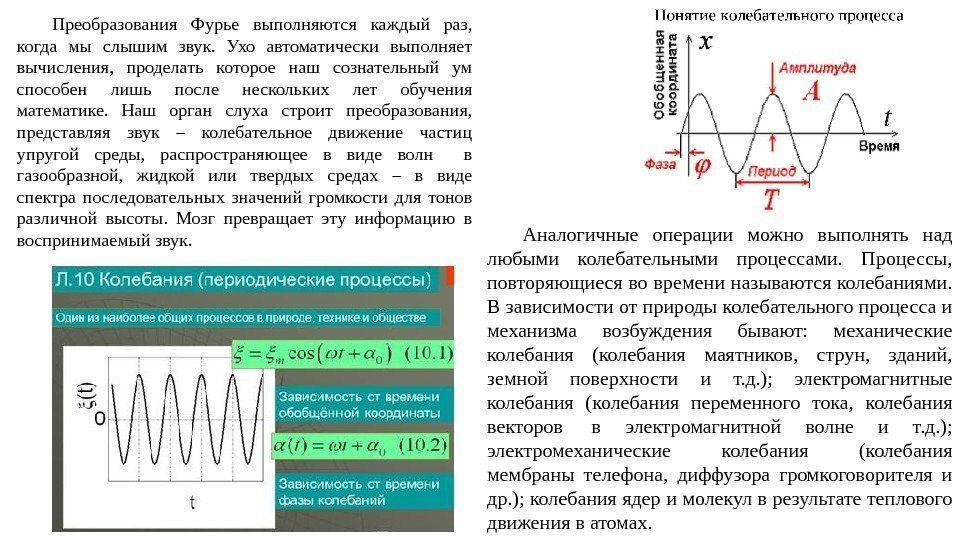
Преобразования Фурье выполняются каждый раз, когда мы слышим звук. Ухо автоматически выполняет вычисления, проделать которое наш сознательный ум способен лишь после нескольких лет обучения математике. Наш орган слуха строит преобразования, представляя звук – колебательное движение частиц упругой среды, распространяющее в виде волн в газообразной, жидкой или твердых средах – в виде спектра последовательных значений громкости для тонов различной высоты. Мозг превращает эту информацию в воспринимаемый звук. Аналогичные операции можно выполнять над любыми колебательными процессами. Процессы, повторяющиеся во времени называются колебаниями. В зависимости от природы колебательного процесса и механизма возбуждения бывают: механические колебания (колебания маятников, струн, зданий, земной поверхности и т. д. ); электромагнитные колебания (колебания переменного тока, колебания векторов в электромагнитной волне и т. д. ); электромеханические колебания (колебания мембраны телефона, диффузора громкоговорителя и др. ); колебания ядер и молекул в результате теплового движения в атомах.

НЕКОТОРЫЕ МОМЕНТЫ ТРИГОНОМЕТРИИ

Определение ряда Фурье Тригонометрический ряд коэффициенты которого вычислены по формулам Фурье, т. е. называется рядом Фурье периодической с периодом 2 π функции. Sx a anxbnxnn n ()cossin 0 12 , sin)( 1 , cos)( 1 , )( 1 0 nxdxxfbnxdxxfann

Определение кусочно-монотонной функции Функция f(x) называется кусочно-монотонной на отрезке [a, b], если этот отрезок можно разбить конечным числом точек на интервалы, в каждом из которых функция монотонна. Примеры кусочно-монотонных функций: 1) sinx 2) cosx 3) ]1, 1[, 2 xxy

Достаточный признак сходимости ряда Фурье Если периодическая с периодом 2 функция 1) кусочно-монотонна, 2) непрерывна на отрезке [- , ] или имеет на нем конечное число точек разрыва 1 -го рода, то ряд Фурье этой функции сходится во всех точках этого отрезка. Сумма полученного ряда S(x) равна значению функции f(x) в точках непрерывности функции, а в точках ее разрыва сумма ряда равна полусумме левостороннего и правостороннего пределов функции, т. е. , если x = c – точка разрыва, то . Sx fcfc xc() ()()

Разложение в ряды Фурье четных функций Если f(x) –четная функция, то функции являются нечетными, а функции -четными при любых п=1, 2, …. Тогда в силу свойства определенного интеграла : , если f(x) – нечетна, и , если f(x) – четна nxxfsin)( nxxfcos)( fxdx() 0 fxdx()()

Продолжение получим Тогда имеем: , где для четной функции. afxdxafxnxdxn 0 00 22 (), ()cos 0 sin)( nxdxxfbn Sx a anxn n ()cos 0 12 afxdxafxnxdxn 0 00 22 (), ()cos

Ряд Фурье нечетной функции Если функция f(x) является нечетной и периодической с периодом 2π , то ее ряд Фурье имеет вид: , где коэффициенты Sxbnxn n ()sin 1 bfxnxdx n 2 0 ()sin

Ряд Фурье периодической с периодом 2 l функции Если функция f(x) имеет период 2 l , где l-любое число, большее нуля, то ее ряд Фурье можно получить из ряда Фурье периодической с периодом 2 π функции, положив . Тогда функция имеет период 2 π. В самом деле: π lt x )()()(t lt fxf )()()2() )2( (t lt fl lt f tl f

Продолжение Разложим в ряд Функцию , а затем вернемся к старой переменной. Имеем , где , , )(t 10 sincos 2 )( n nn l xn b l xn a a x. S l l dxxf l a)( 1 0 l l ndx l xn xf l a cos)( 1 l l ndx l xn xf l b sin)(

Ряд Фурье четной функции Аналогично тому, как получается ряд Фурье периодической с периодом 2π функции, можно получить ряд функции с периодом 2 l. Тогда имеем следующие формулы: , где 1 0 cos 2 )( n n l xn a a x. S l n l dx l xn xf l adxxf l a 00 0 cos)( 2 , )(

Ряд Фурье нечетной функции Если функция является нечетной, то ее ряд Фурье является рядом по синусам и его можно записать в следующем виде: , где 1 sin)( n n l xn bx. S l ndx l xn xf l b 0 sin)(

Разложение в ряд Фурье непериодических функций Если функция не является периодической, то эту функцию доопределяют до периодической. Затем получившуюся периодическую функцию раскладывают в ряд Фурье, который будет сходиться к функции f(x) на промежутке, где задана эта функция, если, конечно, она удовлетворяет условиям достаточного признака сходимости ряда Фурье. При этом доопределить функцию до периодической можно различными способами. В частности, ее можно доопределить как четную или как нечетную. Как это можно сделать, рассмотрим на конкретном примере.

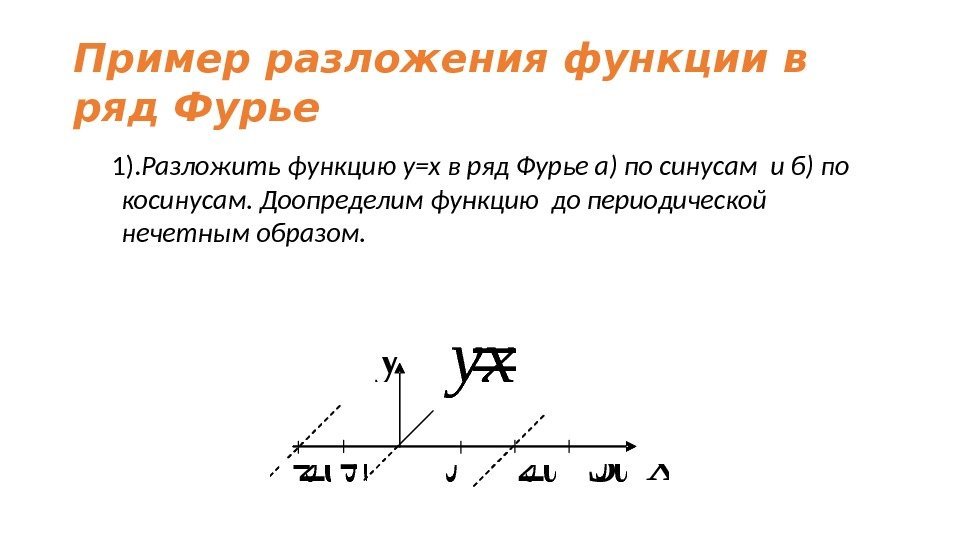
Пример разложения функции в ряд Фурье 1). Разложить функцию у=х в ряд Фурье а) по синусам и б) по косинусам. Доопределим функцию до периодической нечетным образом. x 2 3 — -2 yx y

Решение Тогда , где Вычислим интеграл по частям: Sxbnxn n ()sin 1 bxnxdxn 2 0 sin bxnxdx uxdudx dvnxdxv nx n n 2 0 sin , sin, cos 21 0 0 x nx nn nxdx cos n n nx n n n cos 2 sin 1 cos

Продолжение Таким образом, , а , где или де лиn n bncos 2 1 sincos 2 )( n nxn n x. S n nx x. S n nsin )1(2)( 1 1 x(, )

Продолжение Доопределим теперь f(x) до периодической функции четным образом. Тогда . Sx a anxn n ()cos 0 12 axdx x 0 2 0 22 2 axnxdx uxdudx nxdxdvv nx n n 2 0 cos , cos, sin

Продолжение При четном n выражение в скобках равно нулю и, значит, , а при – нечетном, т. е. при , . Тогда Мы получили разложение функции в ряд Фурье на промежутке (0, ). 2121 0 0 20 xnx nn nxdx n nx sincos 2 0 2 11222 n n n coscoscos an 0 nm 21 a m m 212 4 21 () Sx m m x m () cos() ()