Методы решения тригонометрических уравнений Учитель математики: Семёнова

Методы решения тригонометрических уравнений Учитель математики: Семёнова Елена Юрьевна. МБОУ СОШ № 5 – «Школа здоровья и развития» г. Радужный

Содержание • Метод замены переменной • Метод разложения на множители • Однородные тригонометрические уравнения • С помощью тригонометрических формул: − Формул сложения − Формул приведения − Формул двойного аргумента

Метод замены переменной С помощью замены t = sinx или t = cosx , где t ∈ [− 1; 1] решение исходного уравнения сводится к решению квадратного или другого алгебраического уравнения. См. примеры 1 – 3 2 2 1 1 2 1 t t tg tg cos α α α 221 2 2 t t tg tg sin α α α Иногда используют универсальную тригонометрическую подстановку: t = tg x

Пример 102522 xsin ; tусловиюяетудовлетворне, t tt тогда, ; tгде, txsin. Пусть 21 112 0252 11 21 2 2 1 xsin переменнойисходнойк. Вернемся Zn, narcsinx n π 21 1 Zn, nx nπ 6 π 1. Zn, n: Ответ n π 6 π

Пример 2022 xcosxsinxcos ; t , t tt тогда, ; tгде, tсоsx. Пусть 2 1 1 012 11 21 2 ; xcos , соsx : переменнойисходнойк. Вернемся 2 1 1 Zn, narccosx Zk, kx π2 21π2 то, xcosxsin. Поскольку221 0122 xcosxсоsxcos 0122 xcos Zn, nx Zk, kx π2 3 π2 π2. Zn, n; Zk, k: Ответπ2 3 π2 π

Пример 34 2 3 2 x ctg x tg 31 034 43 0 2 212 tt tt тогда, tгде, tx tg. Пусть ; x tg , x tg переменнойисходнойк. Вернемся 3 2 1 2 то, x tgx ctg. Поскольку 21 2 4 2 3 2 x tg Zk, karctg x Zn, narctg x π3 2 π1 2 Zk, karctgx Zn, nx π32 π 4π 2 Zk, karctgx Zn, nx π232 π2 2 π. Zk, n; karctg; n: Ответπ232π2 2 π

Метод разложения на множители Суть этого метода заключается в том, что произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а другие при этом не теряют смысл: f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0 и т. д. при условии существования каждого из сомножителей См. примеры 4 –

Пример 40 5 2 3 1 xcosxsin ; xcos , xsin 0 5 2 0 3 1 ; xcos , xsin 5 231 Zk, karccosx Zn, narcsinx n π2 5 2 π 31 1 Zk, karccosx Zn, narcsinx n π2 5 2 π π 31 1. Zk, n; karccos; narcsin: Ответ n π2 5 2 ππ

Пример 5 ; xcos , xsin 05 012 ; xcos , xsin 05 21 Zk, kx Zn, narcsinx n π 2 π 5 π 2 1 1 Zk, k x Zn, nx n 5 π 10 π π 6 π 1 0552 xcosxsin 0125 xsinxcos. Zk, k ; Zn, n: Ответ n 5 π 10 π π 6 π

Однородные тригонометрические уравнения Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени. a sin x + b cos x = 0 Замечание. Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0. : cos x a sin x b cos x 0 cos x + cos x = cos x a tg x + b = 0 tg x = – a b

Однородные тригонометрические уравнения a sin 2 x + b sin x cos x + c cos 2 x = 0 Уравнение вида a sin 2 x + b sin x cos x + c cos 2 x = 0 называют однородным тригонометрическим уравнением второй степени. : cos 2 x a tg 2 x + b tg x + c = 0 a sin 2 x b sin x cos x c cos 2 x 0 cos 2 x + cos 2 x = cos 2 x+ cos 2 x Далее, вводим новую переменную tg x = t и решаем методом замены переменной. Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения на множители.

032 xcosxsin xcos xsin 032 tgx 2 3 tgx Zn, narctgxπ 2 3. Zn, narctg: Ответπ 2 3 Пример 7 022 xcosxsin xcos xsin 20 22 22 012 xtg Zn, nxπ 4 π 2. Zn, n : Ответ 2 π 8 π Zn, n x 2 π 8 π xcos: 2 Пример

02322 xcosxsin 0 23 2 2 22 2 xcosxsin xcos xsin 0232 tgxxtg 2 1 023 212 t t tt тогда, ttgx. Пусть ; tgx , tgx : переменнойисходнойк. Вернемся 2 1 Zk, karctgx Zn, nx π2 π 4 π. Zk, n; karctg; n: Ответπ2π 4 π xcos: 2 Пример

032 xcosxsin 03 xcosxsinxcos ; xcos , xcosxsin 0 03 ; Zn, nx , tgx π 2 π 3 1 π 2 π 013 . Zn, nx , Zk, kx ; Zn, nx , Zk, karctgx π 2 π π 6 π π 2 π π 3 1. Zk, n; n; k: Ответπ 2 π π 6 π xcos: Пример

033 3223 xcosxsinxcosxsin 03323 tgxxtgxtg ; Zn, nx , tgx ; tgx , xtg π 4 π 3 1 3 01 0322. Zk, n; k; n: Ответπ 3 π π 4 π 0 33 3 2 3 3 xcosxsin xcosxsin xcos xsin 01312 tgxtgxxtg 0132 tgxxtg . Zn, nx , Zk, kx ; Zn, nx , Zk, karctgx π 4 π π 3 π π 4 π π3 xcos: 3 Пример

23533323322 xcosxsin 0 3 3332 33 2 2 222 xcosxsin xcos xsin 0333232 xtgxtg 3 03 03 0332 3 2 2 22 t tt tt тогда, txtg. Пусть33 xtg переменнойисходнойк. Вернемся Zn, n x Zn, narctgx 3π 9π π 3π 3 π33. Zn, n : Ответ 3 π 9 π xsinxcosxcosxsin 33235333233 2222 03232353332332222 xsinxcosxcosxsin 0333332322 xcosxsinxcos: 32 xsinxcos 3322 Пример

С помощью тригонометрических формул 1. Формулы сложения: sin (x + y) = sinx cosy + cosx siny cos (x + y) = cosx cosy − sinx siny tgx + tgy tg (x + y) = 1 − tgx tgysin (x − y) = sinx cosy + cosx siny cos (x − y) = cosx cosy + sinx siny tgx − tgy tg (x − y) = 1 + tgx tgy сtgx сtgy − 1 сtg (x + y) = сtgу + с tgх сtgx сtgy + 1 сtg (x − y) = сtgу − с tgх

13 xsinxcos. Zn, n: Ответπ2 6 π 3 π 2: 2 1 2 3 xsinxcos тогда, sin, cosчто, Заметим 6 π 2 1 6 π 2 3 2 1 6 π xsinsinxcoscos 2 1 6 π xcos. Zn, narccosx π2 21 6π Zn, nxπ2 6 π 3 π Пример

3 6 π 3 π xcosxsin xsinsinxcoscosxsincosxcossinxcosxsin 6 π 3 π 6 π 33 xcos 1 xcos Zn, nxπ2 Zn, n: Ответπ2 xcosxsinxcos 3 2 1 2 3 Пример

С помощью тригонометрических формул 2. Формулы приведения: ttgt 2π ctg tctgtπctg ttgt 2 3π ctg tctgt 2πctg tctgt 2 π tg ttgtπtg tctgt 2 3π tg ttgt 2πtg tsint 2π cos tcostπcos tsint 2 3π cos tcost 2πcos tcost 2π sin tsintπsin tcost 2 3π sin tsint 2πsin

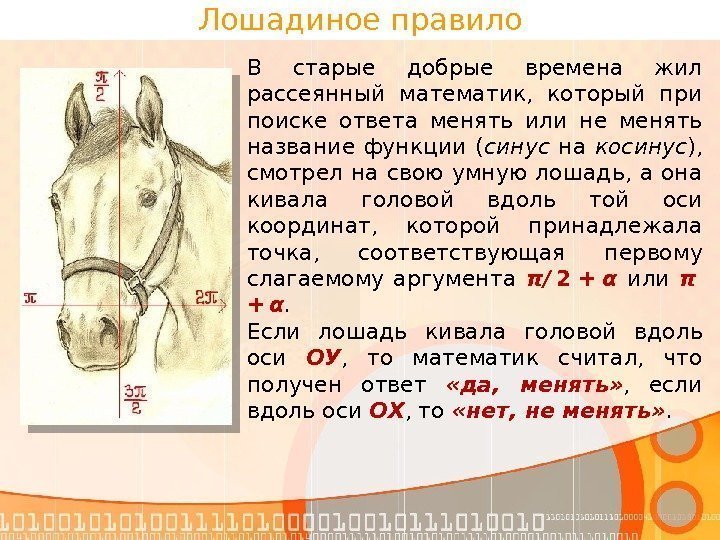
Лошадиное правило В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции ( синус на косинус ), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α. Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .

С помощью тригонометрических формул 3. Формулы двойного аргумента: sin 2 x = 2 sinx cosx cos 2 x = cos 2 x – sin 2 x cos 2 x = 2 cos 2 x – 1 cos 2 x = 1 – 2 sin 2 x tg 2 x = 2 tgx 1 – tg 2 x ctg 2 x = 2 ctgxctg 2 x –

024 xcosxsin. Пример 14 02222 xcosxsin 01222 xsinxcos ; xsin , xcos 0122 02 ; xsin , xcos 2 1 2 02 Zk, karcsinx Zn, nx k π 2 1 12 π 2 Zk, k x Zn, n x k 2 π 1 2 π 4 π. Zk, k ; Zn, n : Ответ k 2 π 1 2 π 4 π

С помощью тригонометрических формул 4. Формулы понижения степени: αα 21 2 12 cossin αα 21 21 2 coscos ααα 2 2 1 sincossin ααα 21 2 sincossin 2 1 2 ααcos sin 2 1 2 ααcos 5. Формулы половинного угла: α αα sin cos sin tg 1 12 α αα sin cos sin ctg

С помощью тригонометрических формул 6. Формулы суммы и разности: 22 2 βαβα βα coscos 22 2 αββα βα sinsincoscos 22 2 βαβα βα cossinsinsin βα βα βα coscos )sin( tgtg βα βα βα sinsin )sin( ctgctg βα αβ βα sinsin )sin( ctgctg

С помощью тригонометрических формул 7. Формулы произведения: βαβαβαcoscos 2 1 βαβαβαcoscossinsin 2 1 βαβαβαsinsincossin

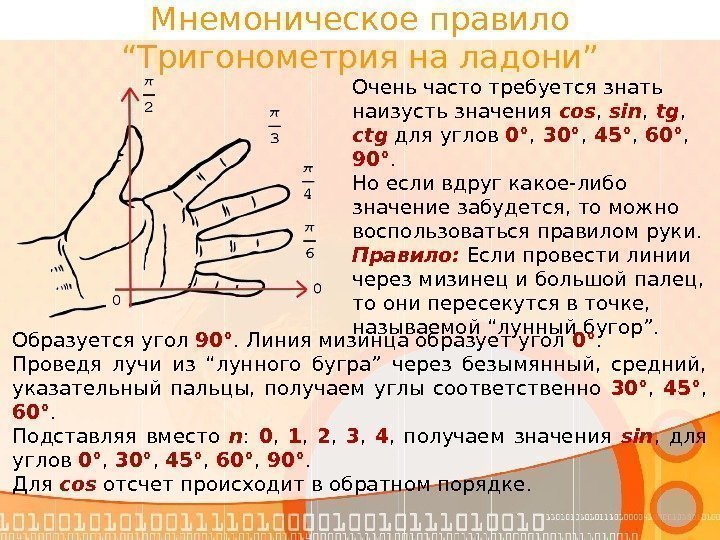
Мнемоническое правило “Тригонометрия на ладони” Очень часто требуется знать наизусть значения cos , sin , tg , ctg для углов 0° , 30° , 45° , 60° , 90°. Но если вдруг какое-либо значение забудется, то можно воспользоваться правилом руки. Правило: Если провести линии через мизинец и большой палец, то они пересекутся в точке, называемой “лунный бугор”. Образуется угол 90°. Линия мизинца образует угол 0°. Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30° , 45° , 60°. Подставляя вместо n : 0 , 1 , 2 , 3 , 4 , получаем значения sin , для углов 0° , 30° , 45° , 60° , 90°. Для cos отсчет происходит в обратном порядке.

Не закончено!