Методы оптимизации Литература 1 Аттетков А В

Методы оптимизации

Литература 1. Аттетков, А. В. Введение в методы оптимизации : [учебное пособие] / А. В. Аттетков, В. С. Зарубин, А. Н. Канатников. — М. : Финансы и статистика : ИНФРА-М, 2008. — 269 с. 2. Корнеенко, В. П. Методы оптимизации / В. П. Корнеенко. — М. : Высшая школа, 2007. — 663, 3. Измаилов, А. Ф. Численные методы оптимизации : учебное пособие / А. Ф. Измаилов, А. Ф. Солодов. — М. : ФИЗМАТЛИТ, 2005. — 304 4. Струченков, В. И. Методы оптимизации : учебное пособие / В. И. Струченков. — М. : Экзамен, 2005. — 256 с. 5. Аттетков, А. В. Методы оптимизации : [учебник для студентов высших технических учебных заведений] / А. В. Аттетков, С. В. Галкин, В. С. Зарубин; под ред. В. С. Зарубина, А. П. Крищенко. — Изд. 2 -е, стереотип. — Москва : МГТУ им. Н. Э. Баумана, 2003. — 440 с. 6. Белоусова Е. П. , Коструб И. Д. Методы оптимизации. Практикум по специальности "Прикладная математика и информатика"

Задача оптимизации Задачей оптимизации называется задача о поиске экстремума функции или функционала на заданном множестве допустимых решений. Любая задача оптимизации включает в себя: • 1. Множество допустимых решений Х, произвольное решение х, принадлежащее Х – допустимое. • 2. Критерий оценки решений f(x). Лучшим (оптимальным) решением называется допустимое решение х*, такое, что f(x*)=extr f(x), ∀х ∈ Х. Экстремум может быть минимумом или максимумом, но стоит рассматривать только задачи минимума функции, поскольку задачи на поиск максимума функции f(x) сводятся к поиску минимума функции (-f(x)).

Классификация методов оптимизации В соответствии с задачами оптимизации: - Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом. - Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции. Существующие в настоящее время методы поиска можно разбить на три большие группы: - детерминированные; - случайные (стохастические); - комбинированные. По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации. По требованиям к гладкости и наличию у целевой функции частных производных: - прямые методы, требующие только вычислений целевой функции в точках приближений; - методы первого порядка : требуют вычисления первых частных производных функции; - методы второго порядка: требуют вычисления вторых частных производных.

Постановка задачи оптимизации, функции одной переменной •

Минимум функции одной переменной •

Унимодальные функции •

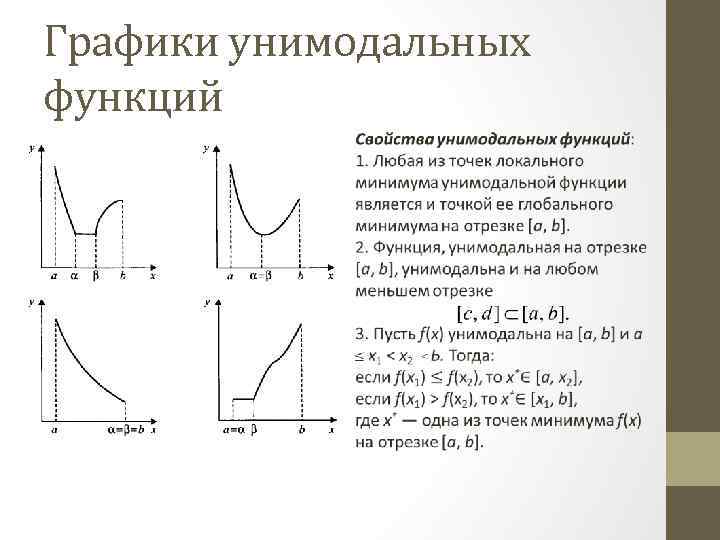Графики унимодальных функций

Унимодальные функции (Примеры) •

Выпуклые функции • Взаимное расположение графика выпуклой функции и хорды

Выпуклые функции (Пример) •

Условие Липшица •

Условие Липшица •

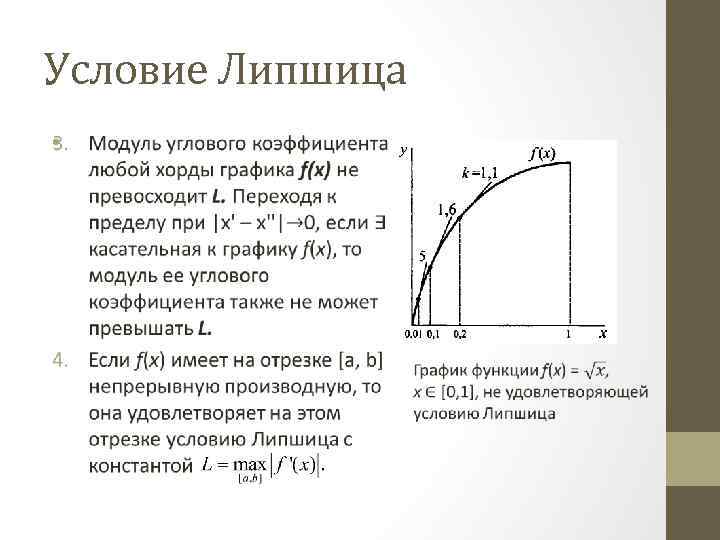Условие Липшица (Пример) •

Классическая минимизация функции одной переменной •

Путь решения задачи минимизации Шаг 1. Находим все точки возможного экстремума f(х) (условие 1)на интервале (а, b), т. е. корни уравнения f'(x) = 0, (стационарные точки f(x), принадлежащие интервалу (a, b)). Шаг 2. Найденные стационарные точки исследуем в соответствии с условием 2, выделяя из них только точки локальных минимумов f(х). Шаг 3. Значения f(х) в точках локальных минимумов и на концах отрезка [a, b] сравниваем между собой. Наименьшему из этих значений соответствует точка глобального минимума f(x) на [а, b].

Минимизация функции одной переменной (Пример) •

Одномерная оптимизация функций. Прямые методы Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации. Большим достоинством прямых методов: - от целевой функции не требуется дифференцируемости; - функция может быть задана аналитически. • Метод перебора • Метод поразрядного поиска • Методы деления отрезка пополам (метод дихотомии и метод золотого сечения) • Метод парабол (метод полиномиальной аппроксимации)

Прямые методы (Примеры) •

Метод перебора •

Метод перебора •

Метод перебора (Пример) • xi 0, 0 0, 1 0, 2 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 1, 0 f(xi) 1, 00 0, 90 0, 82 0, 75 0, 70 0, 67 0, 68 0, 74 0, 86 1, 06 1, 37

Метод поразрядного поиска •

Метод поразрядного поиска (Пример) • x f(x) 1, 000 > 0, 783 > 0, 669 < 0, 789 x f(x) 0, 682 > 0, 669 < 0, 670 < 0, 688 < 0, 726 < 0, 789

Метод поразрядного поиска •

Метод дихотомии •

Метод дихотомии •

Метод дихотомии • - длина отрезка - 1 -ая итерация - 2 -ая итерация - 3 -ья итерация

Метод дихотомии •

Метод дихотомии (Пример) • Номер итерации a b (b-a)/2 x 1 x 2 f(x 1) f(x 2) Сравнение 1 0, 5 0, 49 0, 51 0, 688 0, 670 f(x 1) > f(x 2) 2 0, 49 1 0, 26 0, 735 0, 755 0, 771 0, 792 f(x 1) < f(x 2) 3 0, 49 0, 755 0, 13 0, 633 0, 683 0, 691 f(x 1) < f(x 2) 4 0, 49 0, 633 0, 07 < 0, 1 – точность достигнута

Метод золотого сечения Пусть х2 = τ, тогда симметрично расположенная точка х1 = 1 -τ Пробная точка х1 отрезка [0, 1] перейдет в пробную точку х’ 2 = 1 -τ Иллюстрация выбора пробных точек в нового отрезка [0, τ]. методе золотого сечения Чтобы точки х2 = τ и х’ 2 = 1 - τ делили отрезки [0, 1] и [0, τ] в одном и том же отношении или Длина отрезка Точность определения точки х* Условие окончания поиска

Метод золотого сечения 1. Точки золотого сечения: где каждая из точек х1 и х2 делит отрезок [а, b] на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей части отрезка. 2. На каждой итерации исключения отрезков с пробными точками одна из них переходит на следующий отрезок, и значение f(x) в ней уже известно. 3. Легко проверить, что х1 = а + b - х2 и x 2 = a + b - x 1. На каждой итерации недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке. 4. В качестве приближенного значения х* можно взять середину последнего из полученных отрезков 5. Число итераций (из условия Точность определения х* )

Метод золотого сечения •

Сравнение методов перебора, дихотомии и золотого сечения Значения точности ε(N) в зависимости от количества N найденных значений f(x) на отрезке длиной 1 для трех из рассмотренных методов

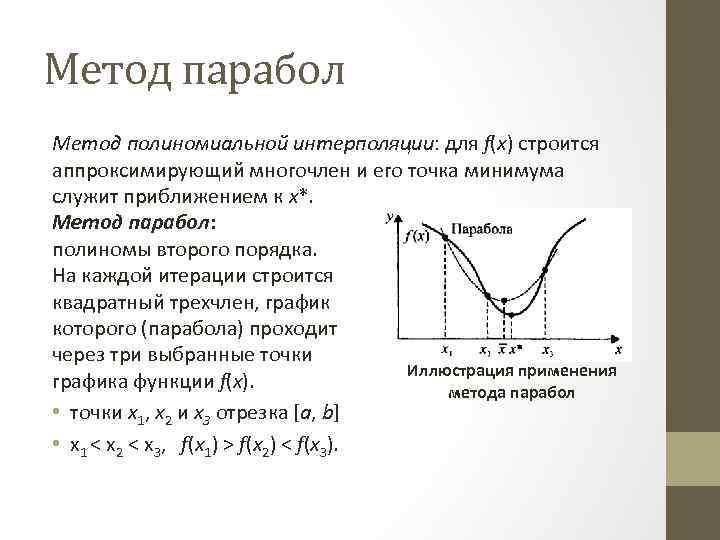Метод парабол Метод полиномиальной интерполяции: для f(x) строится аппроксимирующий многочлен и его точка минимума служит приближением к х*. Метод парабол: полиномы второго порядка. На каждой итерации строится квадратный трехчлен, график которого (парабола) проходит через три выбранные точки Иллюстрация применения графика функции f(x). метода парабол • точки x 1, х2 и х3 отрезка [a, b] • х1 < х2 < х3, f(x 1) > f(x 2) < f(x 3).

Метод парабол • Точка минимума Окончание поиска

Метод парабол (Пример) •

Метод парабол (Пример) •

Метод парабол (Пример) •

ОДНОМЕРНАЯ МИНИМИЗАЦИЯ. МЕТОДЫ, ИСПОЛЬЗУЮЩИЕ ИНФОРМАЦИЮ О ПРОИЗВОДНЫХ ЦЕЛЕВОЙ ФУНКЦИИ •

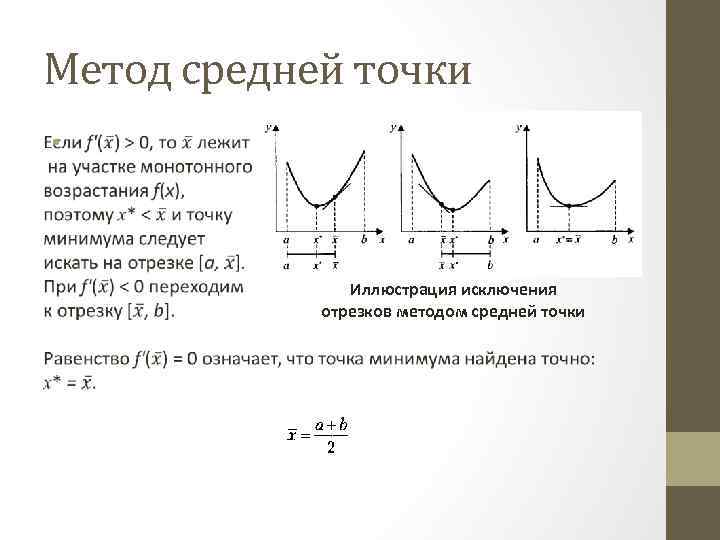Метод средней точки • Иллюстрация исключения отрезков методом средней точки

Метод средней точки •

Метод средней точки (Пример) • Номер итерации a b x 1 0, 5 -0, 107 - 2 0, 5 1 0, 75 1, 215 + 3 0, 5 0, 750 0, 625 0, 441 + 4 0, 5 0, 625 0, 563 0, 142 + 5 0, 563 0, 531 0, 012 Точность достигнута

Метод хорд •

Метод хорд •

Метод хорд (Пример) • Номер итерации a b 1 1 0, 216 -0, 766 - 2 0, 216 1 0, 352 -0, 528 - 3 0, 352 1 0, 435 -0, 319 - 4 0, 435 1 0, 480 -0, 175 - 5 0, 480 1 0, 504 -0, 091 - 6 0 0, 504 1 0, 516 -0, 046 Точность достигнута

Метод Ньютона / Метод касательных • Иллюстрация метода касательных

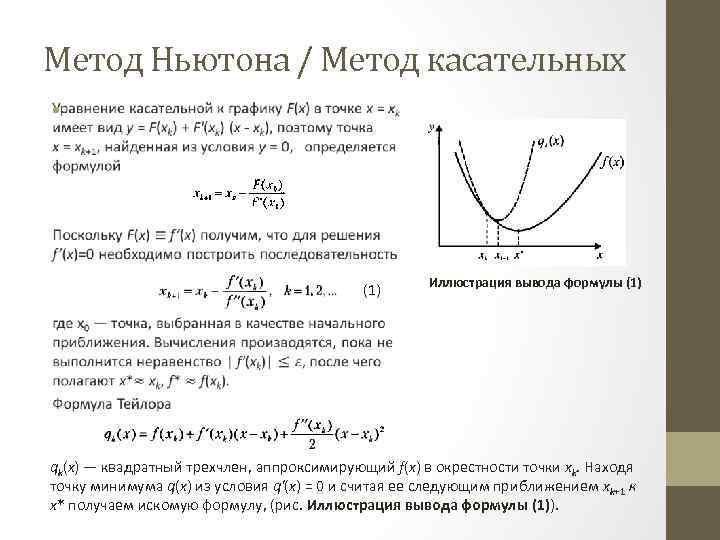Метод Ньютона / Метод касательных • (1) Иллюстрация вывода формулы (1) qk(x) — квадратный трехчлен, аппроксимирующий f(x) в окрестности точки хk. Находя точку минимума q(x) из условия q'(x) = 0 и считая ее следующим приближением xk+1 к х* получаем искомую формулу, (рис. Иллюстрация вывода формулы (1)).

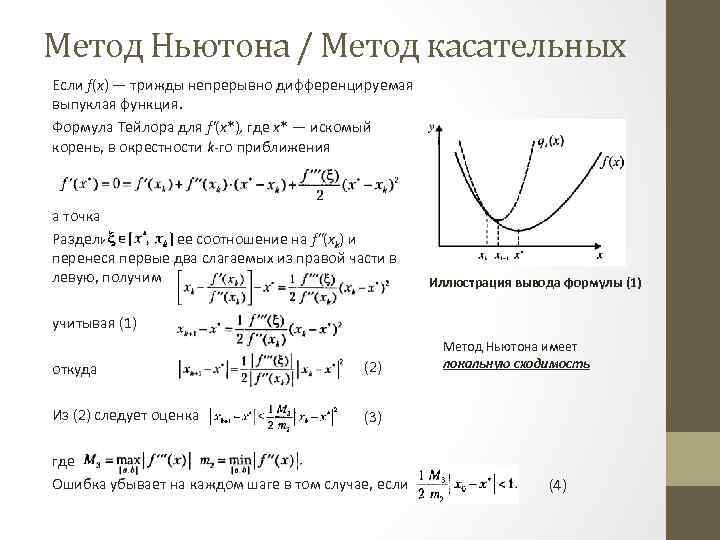Метод Ньютона / Метод касательных Если f(x) — трижды непрерывно дифференцируемая выпуклая функция. Формула Тейлора для f'(x*), где х* — искомый корень, в окрестности k-го приближения а точка Разделив последнее соотношение на f"(xk) и перенеся первые два слагаемых из правой части в левую, получим Иллюстрация вывода формулы (1) учитывая (1) откуда (2) Из (2) следует оценка Метод Ньютона имеет локальную сходимость (3) где Ошибка убывает на каждом шаге в том случае, если (4)

Достаточное условие монотонной сходимости метода Ньютона •

Метод Ньютона (Пример) •

Методы минимизации многомодальных функций. Метод перебора •

Метод перебора Пусть х* — точка минимума f(x) на [a, b]. Среди пробных точек метода перебора найдется такая точка xi, что C учетом условия Липшица можно записать Определение минимума многомодальной функции Если функция f(х) многомодальна, то погрешность определения ее точки минимума может быть значительной, несмотря на то, что сам минимум f* найден достаточно (рис. Определение минимума многомодальной функции).

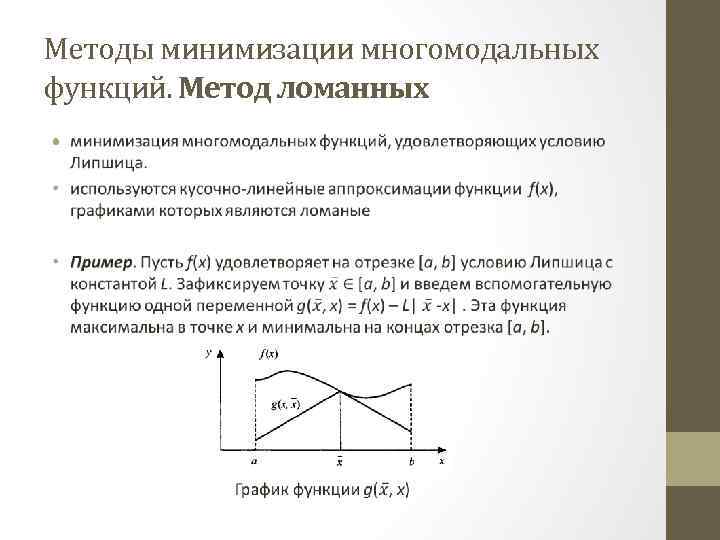Методы минимизации многомодальных функций. Метод ломанных •

Метод ломаных Аппроксимирующие кусочно-линейные функции pk(x), k = 0, 1, . . . строятся следующим образом. Рассмотрим прямые y = f(a) - L(x – a) и y = f(b) + L(x – b). Они пересекаются в точке (х0, у0) с координатами (5) Положим

Метод ломаных Построение ломаных p 0(x), p 1(x), p 2(x) График p 0(x), ее точка минимума х*0 = х0, а минимальное значение p*0(x) = у0 (рис. a). Используя g(х*0 , х), определим аппроксимирующую функцию Появились две новые точки локального минимума х’ 1 и х’’ 1 (рис. б): (6) причем

Метод ломаных Выберем точку глобального минимума p*1 функции р1(х), обозначим ее через х*1 и положим У р2(х) по сравнению с р1(х) вместо х* появились две новые точки локального минимума х’ 2 и х’’ 2 (рис. в): (7) Пусть функция рk-1(х) построена. Выбрав точку глобального минимума р*k-1(х) и обозначив ее через x*k-1(х) Новые точки локального минимума х’k и х’’k, появившиеся взамен х*k-1, а значения рk(х) в этих точках находятся по формулам, аналогичным (6) и (7):

Метод ломаных. Свойства функций pk(x) •

Метод ломаных • (8)

Метод ломаных. •

ЗАДАЧА МИНИМИЗАЦИИ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ БЕЗУСЛОВНОГО ЭКСТРЕМУМА

Постановка задачи поиска минимума функций •

Основные определения •

Основные определения Определение. Матрицей Гессе Н(х) дважды непрерывно дифференцируемой в точке х функции f(х) называется матрица частных производных второго порядка, вычисленных в данной точке где Разложение в ряд Тейлора

Матрица Гессе (Пример) •

Основные определения •

Свойства выпуклых множеств и выпуклых функций •

Свойства выпуклых множеств и выпуклых функций •

Свойства выпуклых множеств и выпуклых функций •

Необходимые условия экстремума первого порядка. •

Необходимые условия экстремума второго порядка. •

Достаточные условия экстремума •

Проверка выполнения условий экстремума •

Критерий Сильвестра проверки достаточных Для того, чтобы матрица Гессе Н(х*) была положительно определенной (Н(х*) > 0) и стационарная точка х* являлась точкой локального минимума, необходимо и достаточно, чтобы знаки угловых миноров были строго положительны Для того, чтобы матрица Гессе Н(х*) была отрицательно определенной (Н(х*) < 0 ) и стационарная точка х* являлась точкой локального максимума, необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с отрицательного

Критерий проверки необходимых условий экстремума второго порядка •

Критерий проверки необходимых условий экстремума второго порядка при поиске безусловного экстремума

Алгоритм решения Шаг 1. Записать необходимые условия экстремума первого порядка и найти стационарные точки х* в результате решения системы n в общем случае нелинейных алгебраических уравнений с n неизвестными. Шаг 2. В найденных стационарных точках х* проверить выполнение достаточных условий, а если они не выполняются, то необходимых условий второго порядка с помощью одного из двух способов. Шаг 3. Вычислить значения f(х*) в точках экстремума. Для функции одной переменной f(x) Если f(x) и ее производные непрерывны, то точка x*является точкой экстремума тогда и только тогда, когда m — четное, где m — порядок первой не обращающейся в нуль в точке х* производной. Если f(m)(x*) > 0, то в точке х* — локальный минимум, а если f(m)(x*) < 0, то в точке х* — локальный максимум. Если число m нечетное, то в точке х* нет экстремума.

Поиск экстремума (Пример) •