МЕТОДЫ ОПТИМИЗАЦИИ Кафедра математических методов в экономике

МЕТОДЫ ОПТИМИЗАЦИИ Кафедра математических методов в экономике

Динамическое программирование • Введение • Формулировка задачи динамического программирования • Принцип оптимальности Беллмана • Алгоритм решения задач динамического программирования • Экономические приложения задач динамического программирования

Введение Динамическое программирование – один из наиболее мощных методов оптимизации. С задачами принятия рациональных решений, выбора наилучших вариантов, оптимального управления имеют дело специалисты разного профиля. Среди методов оптимизации динамическое программирование занимает особое положение. Этот метод исключительно привлекателен благодаря простоте и ясности своего основного принципа – принципа оптимальности. Сфера приложения принципа оптимальности чрезвычайно широка, круг задач, к которым он может быть применен, до настоящего времени еще полностью не очерчен. Динамическое программирование с самого начала выступает как средство практического решения задач оптимизации.

Возникновение этого метода связывают с именем американского ученого Р. Беллмана, который в начале 50 -х годов ХХ века применил к ряду конкретных задач прием, названный впоследствии принципом оптимальности. Основной областью приложения последнего являются многошаговые процессы, т. е. процессы, развивающиеся во времени, что дало основание назвать новый метод оптимизации динамическим. Указанием на динамичность этот метод отличался от линейного и математического программирования, исходная постановка основных задач которых имела статический характер.

Трудно дать четкое определение динамическому программированию. Укажем лишь на три характерные его особенности. Кроме принципа оптимальности, основного приема исследования, большую роль в аппарате динамического программирования играет идея погружения конкретной задачи оптимизации в семейство аналогичных задач. Третьей его особенностью, выделяющей его среди других методов оптимизации, является форма конечного результата. Применение принципа оптимальности и принципа погружения в многошаговых, дискретных процессах приводят к рекуррентно-функциональным уравнениям относительно оптимального значения критерия качества. Полученные уравнения позволяют последовательно выписать оптимальные управления для исходной задачи. Выигрыш здесь состоит в том, что задача вычисления управления для всего процесса разбивается на ряд более простых задач вычисления управления для отдельных этапов процесса. Главным недостатком метода является «проклятие размерности» – его сложность катастрофически возрастает с увеличением размерности задачи.

Формулировка задачи динамического программирования • Дано: – множество состояний • в том числе начальное и конечное – множество возможных переходов из одного состояния в другое • с каждым переходом связывается числовой параметр интерпретируется как затраты, выгода, расстояние, время и т. п. • Найти: – оптимальную последовательность переходов (путь) из начального состояния в конечное • максимум или минимум суммы числовых параметров • предполагается, что хотя бы один путь из начального состояния в конечное существует

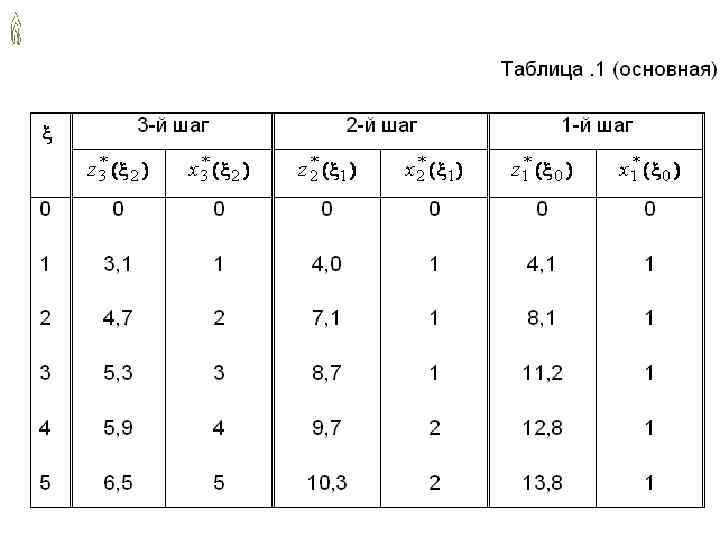
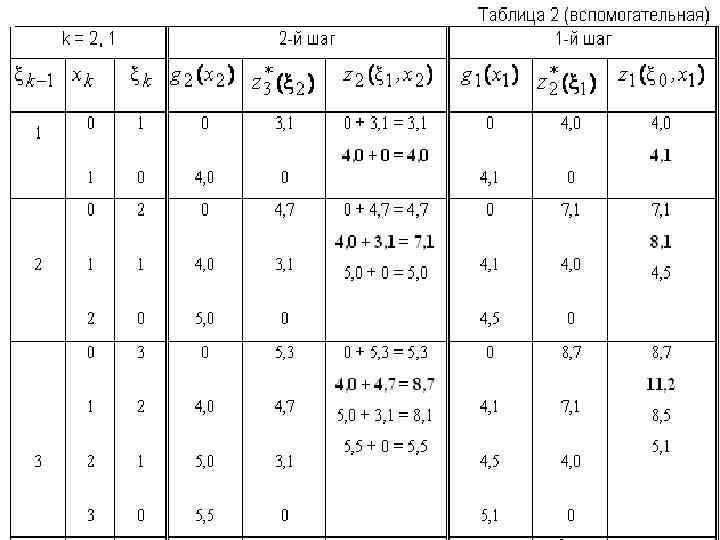
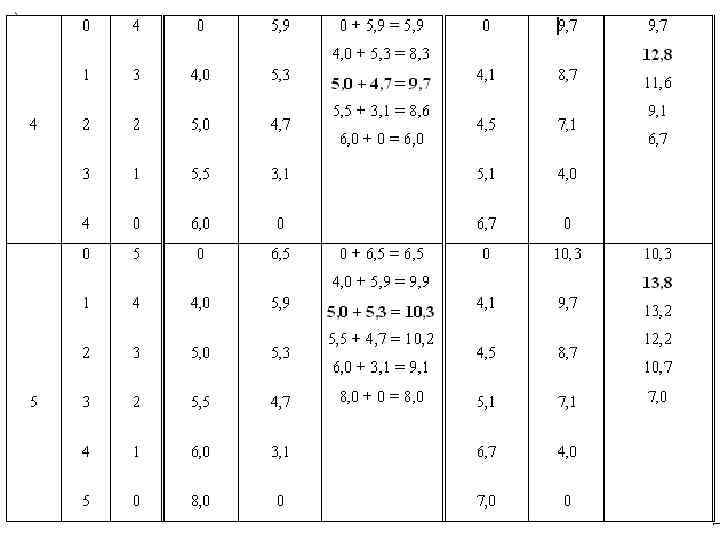
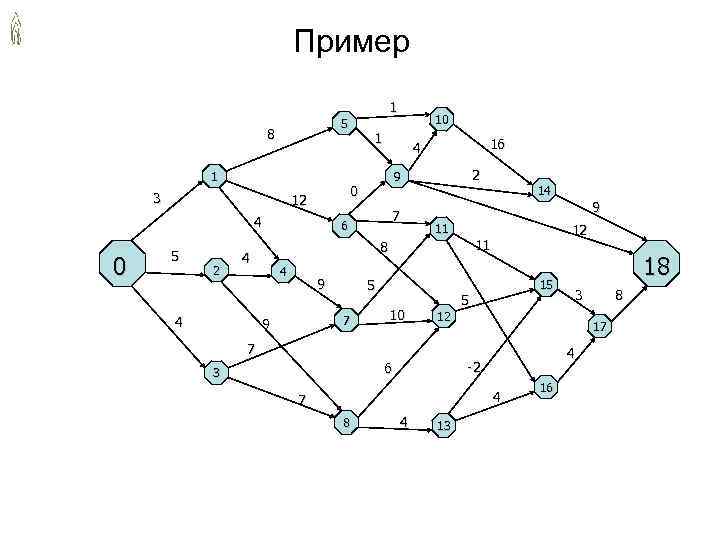Пример 1 5 10 8 1 4 16 1 9 2 0 14 3 12 9 4 7 6 11 12 8 11 5 4 0 2 4 18 9 5 15 5 3 8 4 7 10 12 9 17 4 3 6 -2 16 7 4 8 4 13

сумма числовых значений (eg. расстояний) по всему пути Математическая запись единственность искомого пути: в каждую вершину можно прийти только из одной вершины (или вообще нельзя) если искомый путь пришёл в вершину k, то он должен из Условие целочисленности неё выйти (если только она не конечная) 1, если путь проходит через дугу (i, j) 0, если не проходит или переменных такой дуги нет Например, расстояние между пунктами i и j, км Между вершинами i и j нет дуги. {(1, 2), (1, 3), (2, 4), (2, 5), (3, 5)…}

Принцип оптимальности Беллмана • Если вершины A и B лежат на оптимальном пути между вершинами 0 и X, то часть оптимального пути от 0 до X между вершинами A и B непременно является оптимальным путём от A до B. • Следствие – Чтобы найти оптимальный путь от 0 до A, достаточно исследовать продолжения к A всех оптимальных путей до вершин, предшествующих A – Продолжения неоптимальных путей к предшествующим вершинам можно не просчитывать: они никогда не дадут оптимального пути к A • Принцип Беллмана позволяет построить простую и эффективную вычислительную процедуру для решения задач динамического программирования

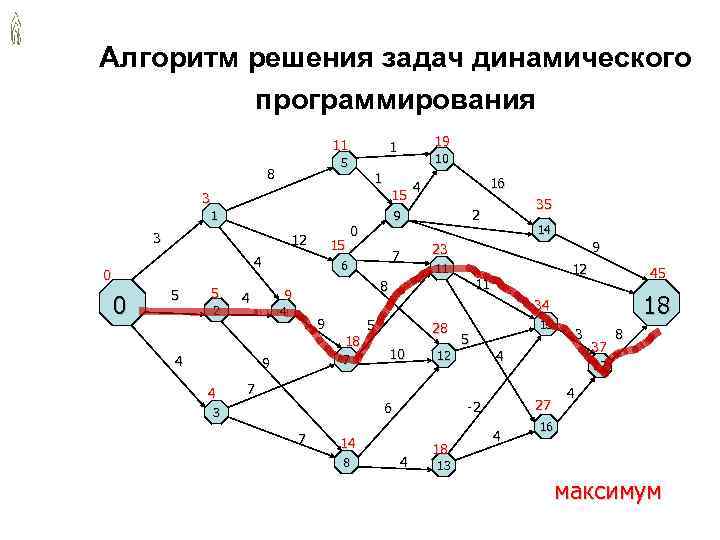Алгоритм решения задач динамического программирования 11 1 19 5 10 8 1 4 16 3 15 35 1 9 2 0 14 3 12 15 23 9 4 7 6 11 12 0 45 8 11 5 5 4 9 0 2 4 34 18 9 5 28 15 18 5 3 8 37 4 7 10 12 4 9 17 4 7 4 6 -2 27 3 16 7 14 18 4 13 максимум

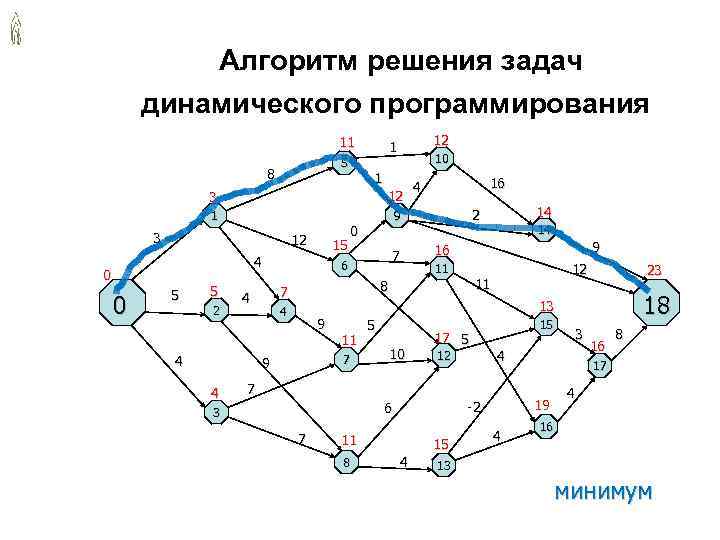Алгоритм решения задач динамического программирования 11 1 12 5 10 8 1 4 16 3 12 1 9 2 14 0 14 3 12 15 16 9 4 7 6 11 12 23 0 5 8 11 5 4 7 0 2 4 13 18 9 5 15 11 17 5 3 8 16 4 7 10 12 4 9 17 4 7 4 6 -2 19 3 16 7 11 4 15 8 4 13 минимум

Экономические приложения • Дуги - работы, которые должны быть выполнены Управление • Параметры – продолжительность работ проектами • Самый длинный путь (max) определяет минимальный срок выполнения проекта Управление • Дуги соответствуют решениям: реновацией • e. g. , эксплуатировать; ремонтировать; списать основных средств • Параметры –доходы производства • Самый выгодный путь (max) определяет жизненный цикл элемента основных средств • Дуги – операции, переводящие фирму в новое состояние Бизнес- • Параметры – доходы (расходы) планирование • Самый выгодный путь определяет наилучший бизнес-план Поиск • Дуги – пути сообщения оптимального • Параметры – время (или стоимость) перевозки маршрута • Самый выгодный (min) путь определяет оптимальную перевозку

Общая постановка задачи динамического программирования

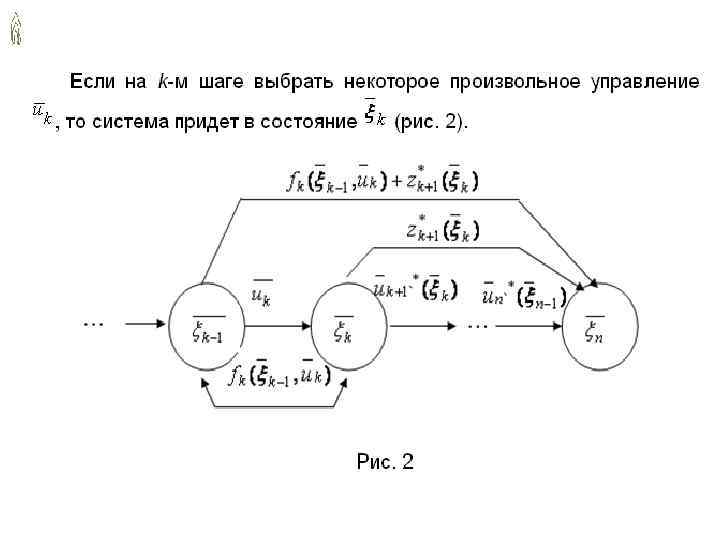
Принцип оптимальности Метод динамического программирования состоит в том, что оптимальное управление строится постепенно. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. Каково бы ни было начальное состояние системы перед очередным шагом, управление на этом этапе выбирается так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.

Уравнение Беллмана.

Экономические задачи