Методы оптимизации 1 2 3 Вопросы Постановка задачи

Методы оптимизации 1. 2. 3. Вопросы Постановка задачи оптимизации Виды задач оптимизации Линейное программирование

1 Постановка задачи оптимизации Методы оптимального планирования используются в различных подсистемах АСУ и являются необходимым средством для их эффективного функционирования. Задачи оптимального планирования можно разделить на задачи объемного (техникоэкономического) планирования и задачи календарного планирования.

n n Первые – являются «внешними» по отношению к объекту планирования. Результатом решения таких задач является производственная программа, которая обеспечивает решение, оптимальное по какому-либо критерию. Вторые – являются внутренними по отношению к объекту планирования. Обязательным являtтся обеспечение технологической последовательности работ

Во всех сферах человеческой деятельности большое место занимает принятие решений. Для этого необходимо выполнить 2 условия: 1. Должно быть не менее 2 -х вариантов. 2. Определен принцип выбора варианта из числа возможных.

Существует два принципа выбора ВОЛЕВОЙ и КРИТЕРИАЛЬНЫЙ n Волевой выбор используется при отсутствии количественных мер оценки вариантов, когда он является единственно возможным. n Критериальный выбор заключается в том, что принимается некоторый критерий и возможные варианты сравниваются по этому критерию.

Вариант, для которого принятый критерий является наилучшим, называется оптимальным, и решение – также называется оптимальным. n Задача принятия наилучшего решения – задача оптимизации. n Критерий оптимизации называют целевой функцией n

2 Виды задач оптимизации В общем случае задача оптимизации может быть записана следующим образом: F=f(xj)→max (min); gi(xj)≤bi(i=1, m); (1) Система (1) представляет собой общий случай математической постановки задачи оптимизации. Она включает целевую функцию F и ограничения gi(xj)≤bi n

n n Суть такой постановки заключается в следующем: необходимо определить такие значения xj, которые находясь в граничных условиях dj≤xj≤Dj удовлетворяли бы ограничениям gi(xj)≤bi и при этом придавали бы целевой функции F=f(xj) искомое оптимальное значение. В каждом конкретном случае система (1) определяется видом переменных xj и зависимостей f(xj) и gi(xj). Различные виды переменных и зависимостей между ними требуют различных методов решения задачи оптимизации.

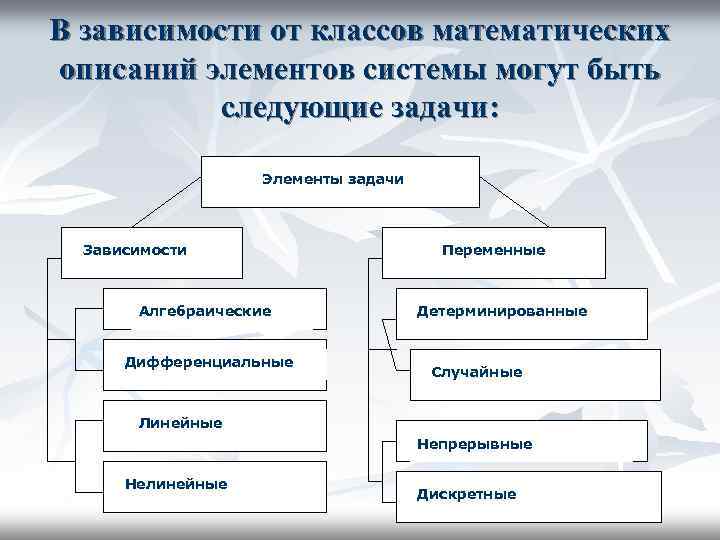В зависимости от классов математических описаний элементов системы могут быть следующие задачи: Элементы задачи Зависимости Алгебраические Дифференциальные Переменные Детерминированные Случайные Линейные Непрерывные Нелинейные Дискретные

n n n Зависимости между переменными входят в ограничения и в целевую функцию. По виду действий над переменными зависимости могут быть алгебраическими и дифференциальными. Задачи, содержащие дифференциальные зависимости в функции времени, называются задачами оптимального управления или – динамической оптимизации.

n n n Линейными называются такие зависимости, в которых переменные или производные находятся в первой степени. Если в зависимостях имеются переменные в степени, отличной от первой, или произведения двух или более переменных, то такие зависимости наз. нелинейными. Задачи оптимизации, содержащие линейные алгебраические зависимости в целевой функции и ограничениях, являются задачами линейного программирования (ЛП).

n Если в задаче оптимизации хотя бы одно ограничение или целевая функция представляют собой нелинейную зависимость, задача является задачей нелинейого программирования (НЛП).

n n Переменные можно подразделить на непрерывные и дискретные, детерминированные и случайные. Если величины в заданном интервале граничных условий могут принимать любые промежуточные значения, они называются непрерывными. Примером непрерывных переменных может служить производительность, стоимость и т. д. Если переменные в заданном интервале могут принимать лишь определенные значения, они называются дискретными.

n n Важным видом дискретных переменных являются булевы переменные, они могут принимать только два значения 0 или 1. С помощью булевых переменных можно решать логические, комбинационные и ряд других специфических задач.

n Дискретные переменные могут быть целочисленными (принимают только целые значения), заданными (например, диаметр трубы должен соответствовать ГОСТУ и быть равным одному из заданных размеров: 100, 150, 200, 250 мм и т. д. )

n n Задачи оптимизации, в которых переменные могут быть только дискретными, называют задачами дискретного или целочисленного программирования (ЦП). Если в задаче часть переменных должна быть целочисленной, а остальные могут принимать непрерывные значения, то такая задача называется задачей частично-целочисленного программирования (ЧЦП).

n n Задачи оптимизации, в которые входят случайные величины, задачами стохастического программирования (СТП). Все рассмотренные классы задач относятся к задачам математического программирования.

3. Линейное программирование

Постановка задачи ЛП n Общая задача ЛП: Найти значения переменных x 1, x 2…. xn, удовлетворяющих ограничениям и обращающих в максимум (минимум) линейную функцию этих переменных постоянные величины

n n n Допустимое решение задачи линейного программирования - это набор значений x 1, x 2…. xn, удовлетворяющих условиям задачи. Множество всех допустимых решений называется областью допустимых решений. Допустимое решение, при котором линейная целевая функция F принимает свое максимальное (минимальное) значение, называется оптимальным.

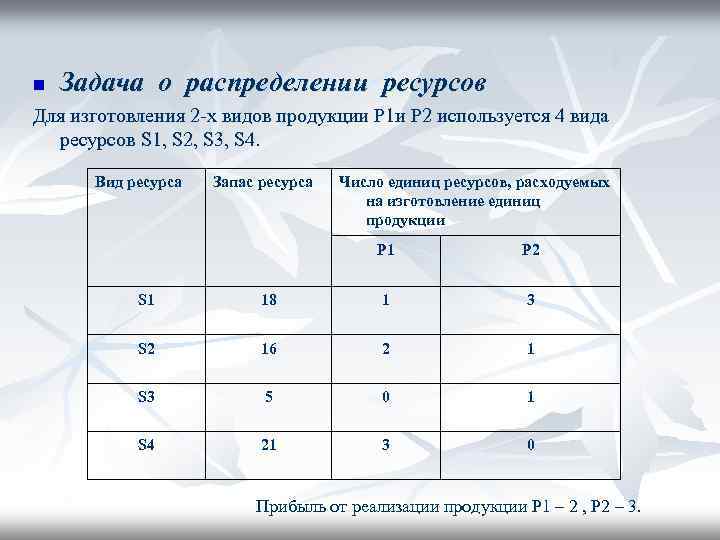n Задача о распределении ресурсов Для изготовления 2 -х видов продукции P 1 и P 2 используется 4 вида ресурсов S 1, S 2, S 3, S 4. Вид ресурса Запас ресурса Число единиц ресурсов, расходуемых на изготовление единиц продукции P 1 P 2 S 1 18 1 3 S 2 16 2 1 S 3 5 0 1 S 4 21 3 0 Прибыль от реализации продукции Р 1 – 2 , Р 2 – 3.

Требуется составить такой план производства продукции, при котором прибыль от реализации будет максимальной. x 1 х2 – число единиц продукции Р 1 и Р 2. Система ограничений будет следующая: х1+3 х2 ≤ 18 2 х1+х2 ≤ 16 х2 ≤ 5 3 х1≤ 21 х1 ≥ 0 х2 ≥ 0 Прибыль составит: F= 2 х1+3 х2 n

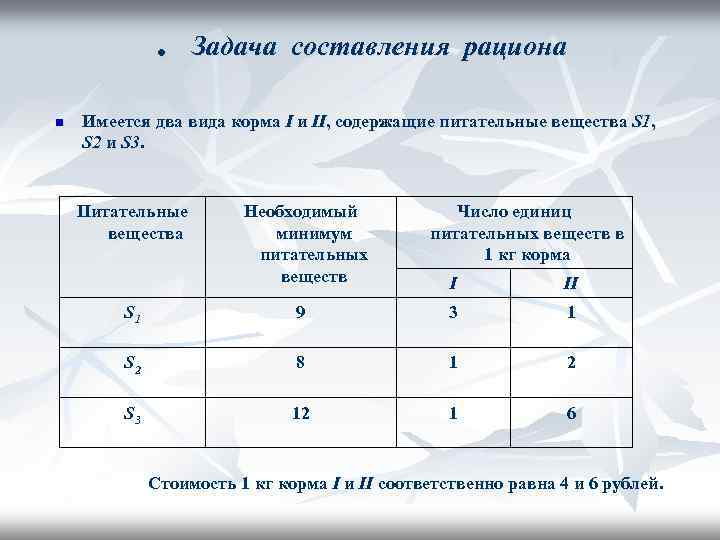. n Задача составления рациона Имеется два вида корма I и II, содержащие питательные вещества S 1, S 2 и S 3. Питательные вещества Необходимый минимум питательных веществ Число единиц питательных веществ в 1 кг корма I II S 1 9 3 1 S 2 8 1 2 S 3 12 1 6 Стоимость 1 кг корма I и II соответственно равна 4 и 6 рублей.

2. Графический метод решения задач линейного программирования n Рассмотрим стандартную задачу линейного программирования с двумя переменными (n=2), состоящую в определении максимального значения функции при условиях:

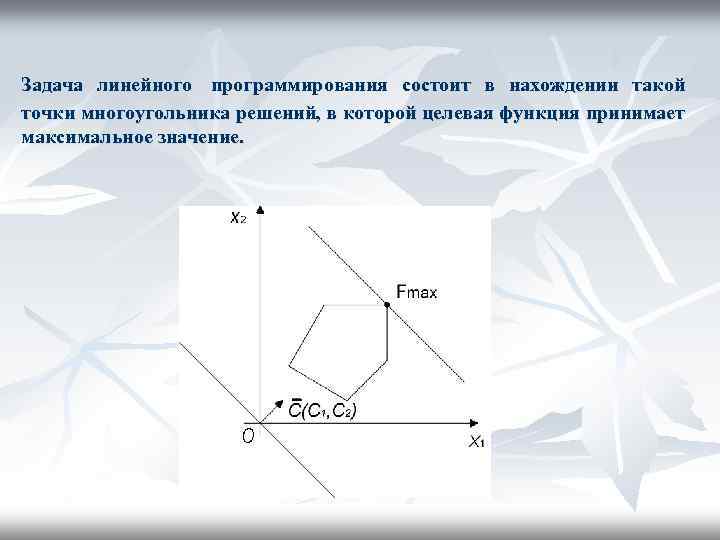Задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное значение.

Исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в котором целевая функция принимает максимальное значение. Эта точка является одной из вершин многоугольника решений n Теорема Если задача ЛП имеет оптимальный план, то ЦФ достигает своего максимального значения в одной из вершин выпуклого многогранника решений. Если ЦФ достигает максимального значения более, чем в 1 -й вершине многогранника, то она достигает это значение и в любой точке, являющейся выпуклой линейной комбинацией этих вершин (в любой точке на прямолинейном отрезке, соединяющем эти вершины). n

Алгоритм решения графическим способом n. В системе координат строятся прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств. n. Находятся полуплоскости, определяемые каждым из ограничений задачи. Определяется многоугольник решений. n. Строится прямая. вектор.

n n Прямая передвигается параллельно в направлении вектора , в результате чего находят точку (точки), в которой целевая функция принимает максимальное значение или устанавливают неограниченность сверху функции на множестве допустимых решений. Определяются координаты точки максимума функции и вычисляется значение целевой функции в этой точке.

Задача о распределении ресурсов n : Необходимо определить максимум функции при условиях

n Найдем полуплоскости, определяемые соответствующими неравенствами и их пересечение. В результате получим многоугольник OABCDE Теперь построим прямую и вектор Перемещаем прямую в направлении вектора. Последней ее общей точкой с многоугольником служит точка С. Координаты С удовлетворяют уравнениям прямых I и II

Ответ n Следовательно, при изготовлении 6 единиц продукции P 1 и 4 единицы продукции P 2, предприятие получит максимальную прибыль, равную 24 рублям

Задача II Составление рациона при условиях:

Решение. n Построим многоугольник решений. Для этого в неравенствах системы ограничений знаки неравенств заменим на знаки равенств:

n Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение построим вектор и прямую Передвигаем в направлении вектора, ближайшей общей точкой с областью допустимых решений является т. А. В этой точке функция F принимает минимальное значение. А – точка пересечения прямых II и I, то ее координаты удовлетворяют уравнениям этих прямых:

Ответ Дневной рацион должен включать в себя 2 кг корма I и 3 кг корма II, при этом затраты будут составлять 26 рублей.

Вопросы 1. 2. 3. 4. 5. Определите общую задачу линейного программирования Определите основную задачу линейного программирования Определите стандартную задачу линейного программирования Теорема Алгоритм решения графическим способом