Методы численного интегрирования (нахождение определенных интегралов) 1.

Методы численного интегрирования (нахождение определенных интегралов)

1. Аналитический метод Где F(x) – первообразная функции ff (( xx )))()(a. Fb. Fx. Fdxxf b a

Аналитический метод интегрирования не всегда может быть применен на практике. Пример «неберущегося» интеграла: b a x dxe

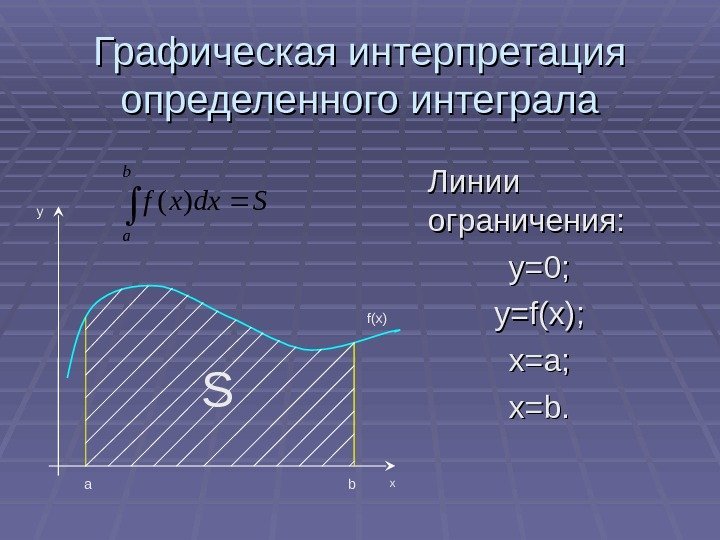
Графическая интерпретация определенного интеграла Линии ограничения: y=0; y=f(x); x=a; x=bx=b. . Sdxxf b a )( xy ba S f(x)

2. Численные методы 1. 1. [a, b] разбивается на на nn равных отрезков длиной hh. . 2. Площадь S S разбивается на на nn полос шириной hh. . 3. Полоса представляется в виде геометрической фигуры. 4. Рассчитывается площадь каждой полосы. 5. Искомый интеграл есть сумма площадей всех полос. xy a f(x)n=10 bx 1 x 2 x i h

1. Метод прямоугольников Отдельно взятая полоса представляется в виде прямоугольника шириной hh. . ВОПРОС: Какая величина принимается за высоту прямоугольника?

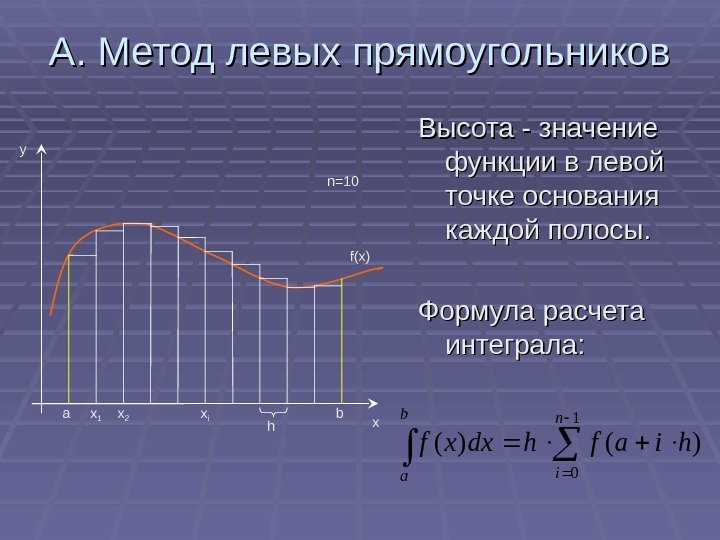
А. Метод левых прямоугольников Высота — значение функции в левой точке основания каждой полосы. Формула расчета интеграла: xy a f(x)n=10 bx 1 x 2 x i h 1 0 )()( n i b a hiafhdxxf

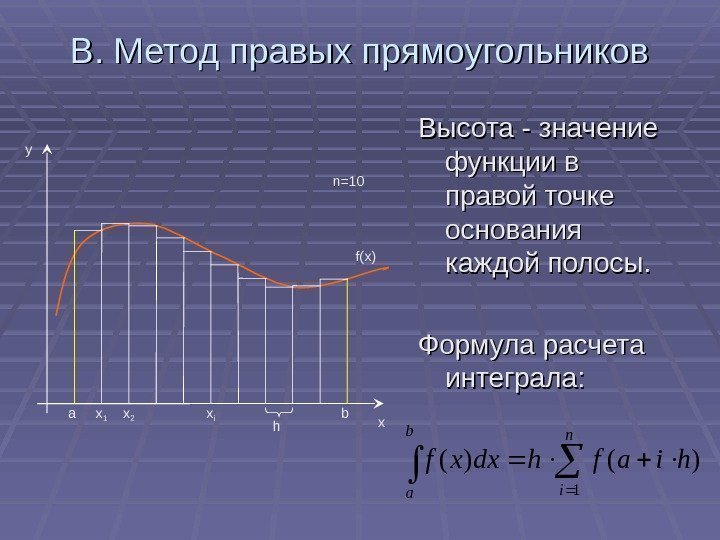
BB. Метод правых прямоугольников Высота — значение функции в правой точке основания каждой полосы. Формула расчета интеграла: n i b a hiafhdxxf 1 )()( xy a f(x)n=10 bx 1 x 2 x i h

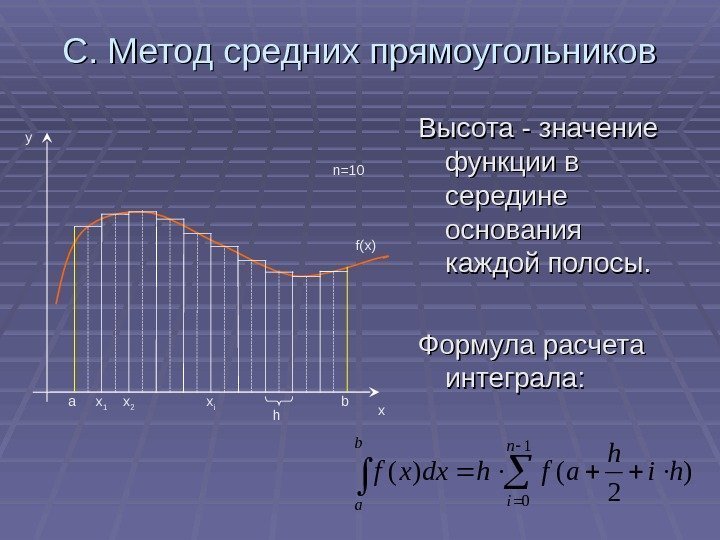
С. Метод средних прямоугольников Высота — значение функции в середине основания каждой полосы. Формула расчета интеграла: 1 0 ) 2 ()( n i b a hi h afhdxxf xy a f(x)n=10 bx 1 x 2 x i h

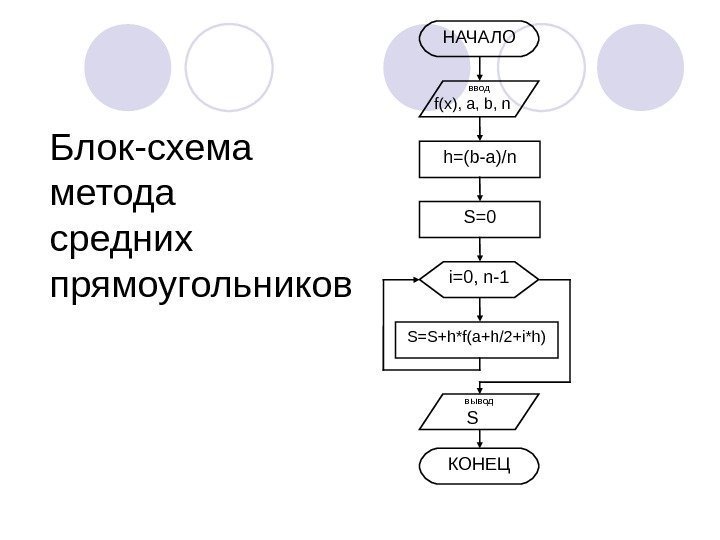
Блок-схема метода средних прямоугольников НАЧАЛО ввод f(x), a, b, n i=0, n-1 h=(b-a)/n S=0 S=S+h*f(a+h/2+i*h) вывод S КОНЕЦ

2. Метод трапеций Отдельно взятая полоса представляется в виде перевернутой трапеции высотой hh. . Основания трапеции будут равны значениям функции в левой и правой точке высоты трапеции. Площадь трапеции: основанияcиc высотаh где cc h. S 21 21 ; ;

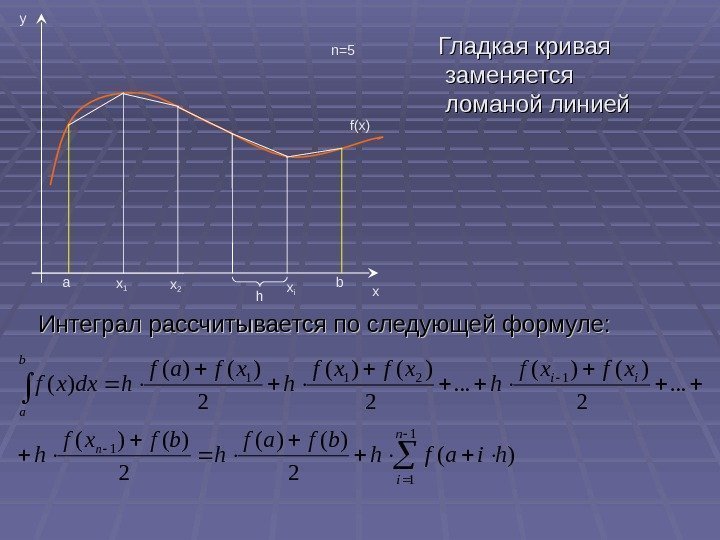
Гладкая кривая заменяется ломаной линией 1 1211 )( 2 )()(. . . 2 )()( )( n ii b a hiafh bfaf h bfxf h xfxf h xfaf hdxxf xy a f(x)n=5 b x 1 x 2 x i h Интеграл рассчитывается по следующей формуле:

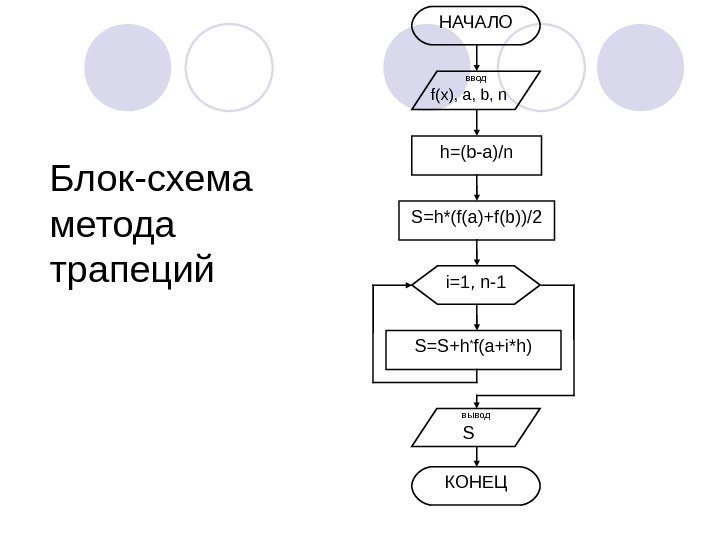
Блок-схема метода трапеций НАЧАЛО ввод f(x), a, b, n i=1, n-1 h=(b-a)/n S=h*(f(a)+f(b))/2 S=S+h * f(a+i*h) вывод S КОНЕЦ

33. Метод Симпсона Гладкая функция заменяется участками парабол. Через любые 3 точки на плоскости можно провести одну и только одну параболу. Парабола проводится через точки пересечения границ 2 -х соседних полос с графиком подынтегральной функции.

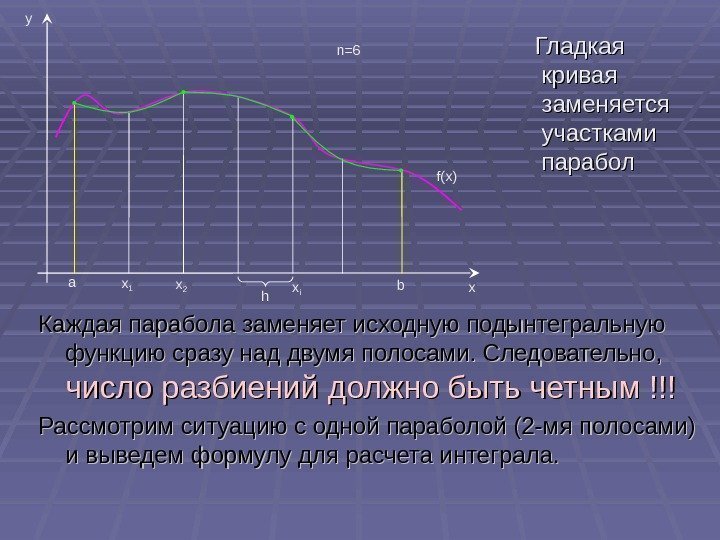
Гладкая кривая заменяется участками парабол Каждая парабола заменяет исходную подынтегральную функцию сразу над двумя полосами. Следовательно, число разбиений должно быть четным !!! Рассмотрим ситуацию с одной параболой (2 -мя полосами) и выведем формулу для расчета интеграла. xy a f(x)n=6 bx 1 x 2 x i h

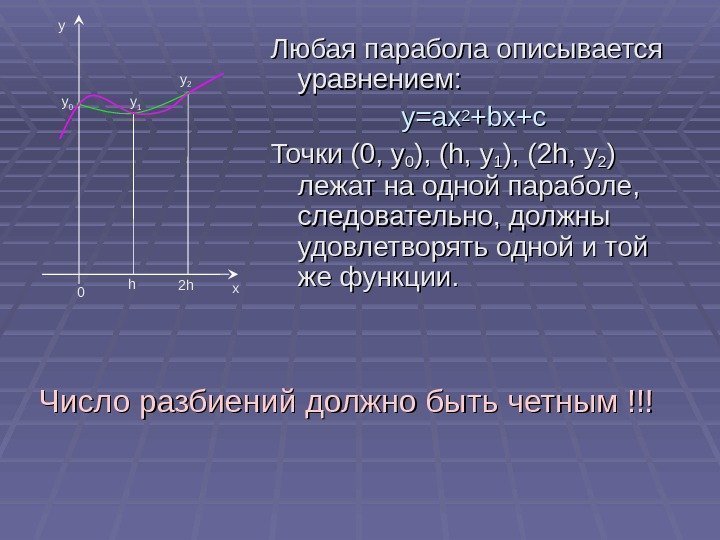
Любая парабола описывается уравнением: y=ax 22 +bx+c Точки (0 , y, y 00 ), ), (( h, y 11 ), ), (( 2 h, y 22 ) ) лежат на одной параболе, следовательно, должны удовлетворять одной и той же функции. Число разбиений должно быть четным !!! xy 0 h 2 hy 0 y 1 y

Подставляем координаты 3 -х точек в уравнение для параболы, получаем систему линейных алгебраических уравнений. Здесь неизвестные — параметры параболы: a, b, c. Из 1 -го уравнения: yy 00 =c. Произведя замену, получим новую систему уравнений: Решаем полученную СЛАУ методом Крамера: 22 12 02 2)2( 00 ychbha ycba 02 2 01 2 2)2(yyhbha

Выведем формулу для расчета коэффициентов aa и и b b : : hh hh yyh b hh hh hyy a 2)2( ; 2)2( 2 2 2 01 2 2 2 02 01 2 102 33 0201 22 02 01 2 2 42 )()(2 2)2( 2 h yyy hh yyhyyh hh hh hyy a h yyy hh yyhyyh hh hh yyh b 2 34 42 )(4)( 2)2( )2(

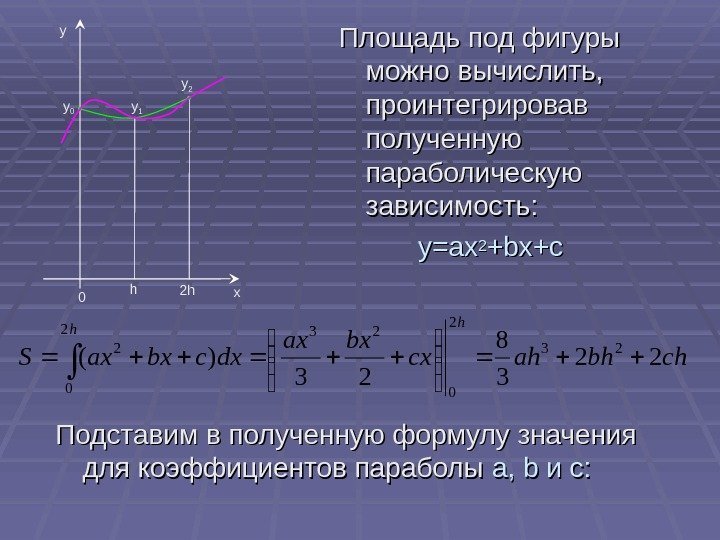
Площадь под фигуры можно вычислить, проинтегрировав полученную параболическую зависимость: y=ax 22 +bx+c xy 0 h 2 hy 0 y 1 y 2 chbhahcx bxax dxcbxax. S h h 22 3 8 23 )( 232 0 2 Подставим в полученную формулу значения для коэффициентов параболы aa , , bb и и cc : :

Получим: Если число разбиений будет не 2, а 4, то формула для вычисления интеграла будет иметь следующий вид: )4( 3 2)34()2( 34 2 2 2 38 210 0021102 02 0213 2 102 yyyh hyyyyh hyh h yyy S )424( 3 )4( 3 43210432210 yyyyy h S

В общем виде: Формула Симпсона)24( 3 )42. . . 2424( 3. . 0 1243210 nчетннечетн nnn yyyy h S

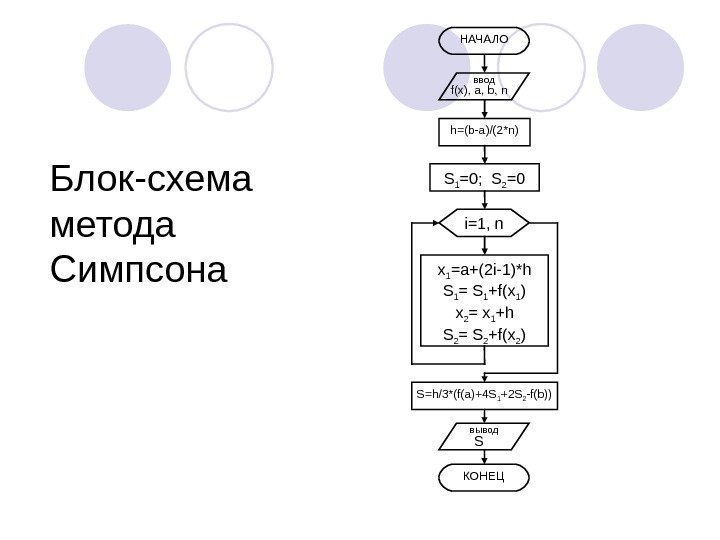
Блок-схема метода Симпсона НАЧАЛО ввод f(x), a, b, n i=1, nh=(b-a)/(2*n) S 1 =0; S 2 =0 x 1 =a+(2 i-1)*h S 1 = S 1 +f(x 1 ) x 2 = x 1 +h S 2 = S 2 +f(x 2 ) КОНЕЦ вывод SS=h/3*(f(a)+4 S 1 +2 S 2 -f(b))

Замечания оо погрешности численного интегрирования

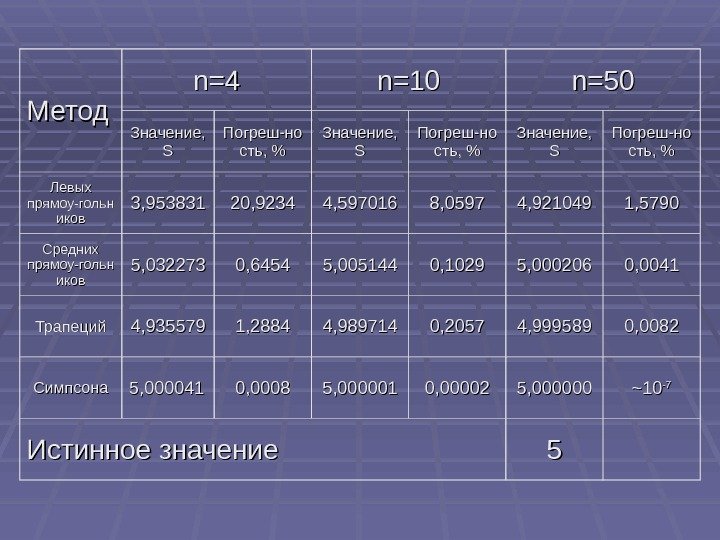
Для оценки погрешности численного интегрирования сравним значения интеграла, рассчитанные различными численными методами с истинным значением интеграла, рассчитанным аналитически. Пример: Истинное значение: S=5 S=5 4/ 0 2 sin 10 xdx

Метод nn =4=4 nn == 1010 n=50 Значение, SS Погреш-но сть, %сть, % Значение, SS Погреш-но сть, % Левых прямоу-гольн иков 3, 953831 20, 9234 4, 597016 8, 0597 4, 921049 1, 5790 Средних прямоу-гольн иков 5, 032273 0, 6454 5, 005144 0, 1029 5, 000206 0, 0041 Трапеций 4, 935579 1, 2884 4, 989714 0, 2057 4, 99589 0, 0082 Симпсона 5, 000041 0, 0008 5, 000001 0, 00002 5, 000000 ~~ 1010 -7 -7 Истинное значение

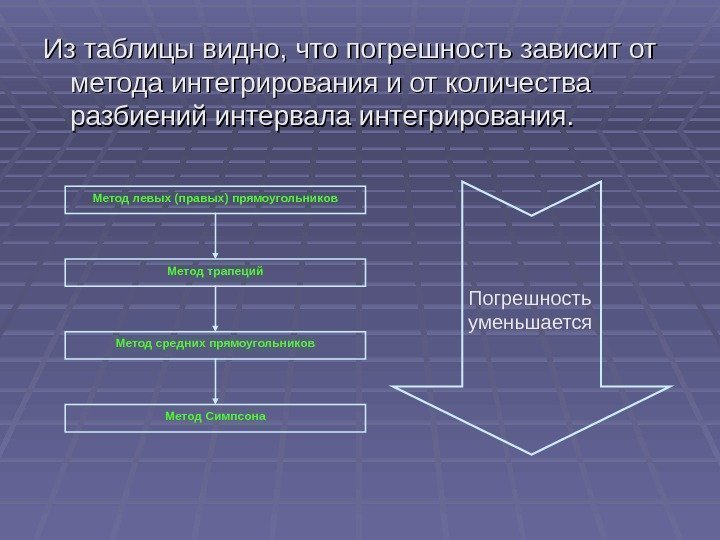
Из таблицы видно, что погрешность зависит от метода интегрирования и от количества разбиений интервала интегрирования. Метод левых (правых) прямоугольников Метод трапеций Метод средних прямоугольников Метод Симпсона Погрешность уменьшается

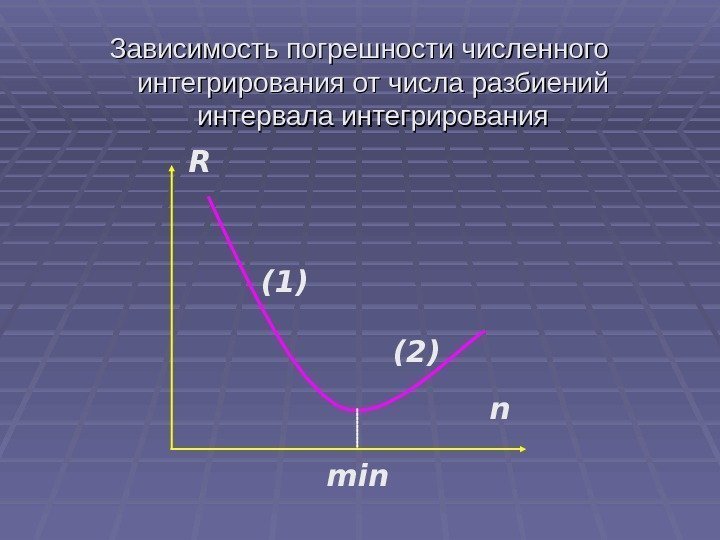
Зависимость погрешности численного интегрирования от числа разбиений интервала интегрирования n. R min(1) (2)