Методика проведения анализа стохастических факторных систем Понятие стохастической

Методика проведения анализа стохастических факторных систем Понятие стохастической связи и задачи корреляционного анализа. Способ парной корреляции. Регрессионный анализ Множественный корреляционно-регрессионный анализ. Анализ временных рядов Вероятностный анализ и его использование в АХД

Понятие стохастической связи Стохастическая (вероятностная, корреляционная) зависимость характеризуется тем, что связи между факторами и результатом их взаимодействия не имеют постоянной формы, а носят случайный вероятностный характер. Выявление формы связи, то есть ее моделирование, осуществляется на основе выборочного наблюдения за последовательностью однородных, повторяющихся явлений путем исчисления средних для данной выборки характеристик. По связи между этими средними судят о характере зависимости в целом.

Способы исследования стохастических связей Для исследования стохастических связей используются стандартные способы статистического анализа: сравнение, параллельных и динамических рядов, аналитические группировки, графики. Однако они не дают возможности определить влияние каждого фактора на результативный показатель, т.е. провести факторный анализ. Для этой цели используются способы: корреляционного, дисперсионного, компонентного, многомерного факторного анализа. Наиболее широко используются методы корреляционно-регрессионного анализа. Необходимым условием их применения являетя наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий период по совокупности однородных объектов).

Сущность корреляционного анализа Стохастическое исследование связи между показателями происходит с помощью методов корреляционного анализа коэффициентов и отношений корреляции. В переводе с латинского correlatio означает "соотношение, взаимная связь, взаимозависимость. Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Парная корреляция – связь между двумя показателями, один из которых является факторным, а другой – результативным. Множественная корреляция – взаимодействие нескольких факторов с результативным показателем.

Необходимые условия применения корреляционного анализа наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов). исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации

Приемы корреляционного анализа В зависимости от характера исходной информации применяются разные приемы корреляционного анализа: оценка парной корреляции между показателями с цифровой шкалой измерения; ранговая корреляция и коэффициенты, рассчитанные по так называемым матрицам сопряженности при анализе связей между качественными показателями; каноническая корреляция при анализе связи между группами показателей разной размерности; частная корреляция, позволяющая исследовать связь между двумя показателями путем элиминирования (устранения) искажающего влияния на совместный одинаковый характер изменения (варьирования) двух показателей при общих для них одного или нескольких факторах; множественная корреляция при оценке зависимости одного результативного показателя от группы факторов-аргументов.

Задачи корреляционного анализа определить изменение результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении), то есть определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу; установить относительную степень зависимости результативного показателя от каждого фактора. Для решения первой задачи подбирается соответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи. Легче всего определить тип модели используя графический анализ

Способ парной корреляции В случае, если графический анализ показывает зависимость между фактором и результатом, можно использовать корреляционный анализ для оценки степени близости фактических точек разброса к функции того или иного вида

Парная корреляция при линейной зависимости Прямолинейную зависимость характеризует уравнение прямой: Y = a + bx где х – факторный показатель, Y – результативный показатель, a – постоянная величина результативного показателя, которая не связана с изменением данного фактора, b – показывает среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения. При такой связи с изменением факторного показателя на определенную величину результативный показатель равномерно возрастает или убывает. При криволинейной зависимости между изучаемыми явлениями уравнение связи решается по такому же принципу. Уравнение может быть уравнением гиперболы, параболы и т.д. Степень "прямолинейности" можно измерить с помощью Присоновского коффициента корреляции (линейного коэффициент корреляции r). Для линейной функции значение r находится в пределах от +1 до –1. Этот коэффициент измеряет тесноту связи с линейной зависимостью.

Ранговая корреляция Используется если значения показателей нельзя численно измерить (например, при тестировании кандидатов или абитуриентов). Тогда ряды строят путем ранжирования (определения номера места) показателя в ряду. Далее находятся разницы между парами рангов (d) и коэффициент ранговой корреляции r (коэффициент Спирмена), где n – число значений в ряду.

Проверка линейности связи .В корреляционном анализе установлено, что связь считается тесной при коэффициенте корреляции более 0,7 и средней, если он находится в пределах от 0,5 до 0,7. Коэффициент детерминации (возведенный в квадрат коэффициент корреляции) можно использовать для количественного определения характеристики, связывающей фактор и результат. Например, Если коэффициент детерминации = 0,64 при расчете зависимости объема реализации от расходов на рекламу, то можно говорить о том, что 64% изменений в объеме реализации связаны с изменением расходов на рекламу.

Проверка линейности связи при анализе небольшого количества данных Коэффициенты корреляции, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться под действием случайных причин. Поэтому необходима проверка их сущности. Для оценки значимости r применяется t-критерий Стьюдента. При этом определяется фактическое значение критерия tr и сравнивается с критерием tк, которое берется из справочника

Корреляционный анализ нелинейных связей Для нелинейных зависимостей оценка тесноты связи производится путем исчисления корреляционного отношения, которое можно применять при любой форме зависимости, однако для его исчисления сначала необходимо с помощью регрессионного анализа функцию и рассчитать выровненные значения результативного показателя У(Х). При истолковании получившихся значений необходимо оценивать результат с точки зрения логики. Например, при расчете двух рядов был получен весьма высокий коэффициент корреляции, однако явной причинной зависимости между рядами не наблюдается. Это может быть связано с тем, что оба эти ряда зависят от одной и той же третьей величины (фактора), который при анализе во внимание не принимался.

Регрессионный анализ Определение аналитической формы связи означает, что моделирование значений результативных показателей осуществляется под влиянием факторных показателей. При стохастическом подходе такая задача решается методом регрессионного анализа. Слово "регрессия" (латинское regressio) означает "движение назад". В отличие от корреляционного анализа, при котором выявляются связи, зачастую, между случайными величинами, при регрессионном анализе ставится задача нахождения средней величины случайной переменной в том случае, если величина другой переменной (или других переменных - в зависимости от поставленной задачи) известна. Регрессионный анализ включает в себя три этапа: построение модели (аналитического уровня) взаимосвязи результативного показателя с взаимодействующими факторами; решение принятой модели путем нахождения параметров регрессионного управления; оценка и анализ полученных результатов. Линия регрессии – это линия наилучшего соответствия, проходящая через точки графика разброса.

Регрессия при линейной зависимости Уравнение линии регрессии при линейной зависимости могут быть рассчитаны на основе решения уравнения: y = a + bx по формулам:

Регрессия при параболической зависимости Уравнение линии регрессии при параболической зависимости могут быть рассчитаны на основе решения уравнения: по формулам:

Регрессия при гиперболической зависимости Уравнение линии регрессии при гиперболической зависимости могут быть рассчитаны на основе решения уравнения: по формулам:

Анализ чувствительности методом корреляционно-регрессионного анализа Чувствительность (эластичность) - мера реагирования одной переменной величины на изменение другой, т.е. число, показывающее процентное изменение одной переменной в результате однопроцентного изменения другой переменной. Например: ∆Xp = P/X * ∆X/ ∆P = (∆X/X) / (∆P / P) где ∆Xp – чувствительность (эластичность) показателя Х к изменению цены Р. Показателем Х могут быть: объем продаж в натуральном выражении или дефлированных ценах, себестоимость в дефлированных ценах и т.п. ∆X – абсолютное изменение показателя Х, связанное с изменением средней цены; Р – средняя цена отчетного периода либо темп инфляции. ∆P - абсолютное изменение средней цены.

Пример корреляционно-регрессионного анализа чувствительности Для данного примера индекс цен можно считать независимой величиной, так как она не зависит от других рассматриваемых признаков. Соответственно объем продаж – величина зависимая, так как он зависит от цен на товар. Независимый показатель является факторным (Х), зависимый – результативным (Y).

Пример корреляционно-регрессионного анализа чувствительности Если знаки отклонений совпадают, следовательно, зависимость прямая, если не совпадают ( как в примере) – обратная Коэффициент детерминации r2 = 0,54, т.е. изменение результативного показателя на 54% объясняется изменением цены, а остальные 46% - другими неучтенными факторами.

Пример корреляционно-регрессионного анализа чувствительности (продолжение) Уравнение линии регрессии y = a + bx рассчитываем по формулам: 5а +1950 b =900 1950 a + 1042500 b = 334750 a = 202,5. и b = 0,0576 Уравнение регрессии примет вид ŷ = 202,5+0,0576x на его основе рассчитаем теоретические значения объема продаж ŷ и используемих для прогноза

Этапы множественного корреляционно-регрессионного анализа Определяются факторы, которые оказывают воздействие на изучаемый показатель и выбираются наиболее существенные. Собирается и оценивается исходная информация (проверяется на точность, однородность, соответствие нормальному закону распределения). Изучается соответствие закону нормального распределения. Изучается характер и моделируется связь между факторами и результатом Проводится расчет основных показателей связи корреляционного анализа (коэффициентов в функции) Дается статистическая оценка результатов корреляционного анализа, т.е. рассчитываются отклонения фактических значений от рассчитанной по формуле величины. Практическое применение модели для прогнозирования и планирования величины показателя, так и для проведения факторного анализа

Множественный корреляционно-регрессионный анализ (этап 1) Определяются факторы, которые оказывают воздействие на изучаемый показатель и выбираются наиболее существенные. При отборе факторов необходимо выбирать только самые существенные. Факторы, которые критерий надежности по Стьюденту меньше табличного в расчет принимать не рекомендуется. Все выбранные факторы должны быть количественно измеримы и информация о них должна содержаться в учетных документах. Нельзя включать в модель взаимосвязанные факторы, т.е. такие, парный коэффициент корреляции между которыми больше 0,85.

Множественный корреляционно-регрессионный анализ (этап 2) Собирается и оценивается исходная информация (проверяется на точность, однородность, соответствие нормальному закону распределения). Критерием однородности служат среднеквадратичное отклонение (σ ) и коэффициент вариации (V). Принято считать, что изменчивость вариационного ряда незначительна, если коэффициент вариации до 10%, средняя – 10-20%, значительная 20-33%, выше – информация неоднородна, из нее необходимо исключить нетипичные наблюдения, которые бывают в начале и в конце ранжированного ряда наблюдений.

Множественный корреляционно-регрессионный анализ (этап 2) Необходимый объем выборки данных (n) для корреляционного анализа проводят по следующей формуле: где V - вариация, в %, t - показатель надежности связи (определяется по специальным таблицам в зависимости от вероятности отклонения, так для вероятности в 5% он составляет 1,96), m – показатель точности расчетов в %, которая для экономических расчетов составляет обычно 5-8%,

Множественный корреляционно-регрессионный анализ (этапы 3 и 4) Изучается соответствие закону нормального распределения, т.е. масса собранных данных должна группироваться вокруг среднего значения. Рассчитываются показатель асимметрии А (он должен быть равен 0, отрицательный - говорит о том, что преобладают значения выше среднего и наоборот) и показатель эксцесса Е (должен быть равен 0, положительное Е – островершинный график, отрицательное - плосковершинный.) Изучается характер и моделируется связь между факторами и результатом, т.е. подбирается математическое выражение, наиболее точно отражающее сущность исследуемой зависимости. Для обоснования функции используются те же приемы, что и в однофакторном анализе, однако поскольку процесс более сложен, его проводят обычно на ЭВМ по типовым программам.

Множественный корреляционно-регрессионный анализ (этапы 3 и 4) Временной лаг (t)- промежуток времени, через который проявляется реакция динамической системы на какой-то фактор. Рассчитывая временной лаг, строится взаимокорреляционная функция по времени и выявляется максимальное ее значение, величина переменной, при котором значение взаимокорреляционной функции rxy максимально. Иногда эта функция имеет несколько максимумов. Это говорит о периодичности, цикличности процесса, что также необходимо учитывать при прогнозировании. При прогнозировании используется функция y=f(x+t)

Множественный корреляционно-регрессионный анализ (этапы 5,6,7) Проводится расчет основных показателей связи корреляционного анализа (коэффициентов в функции) Дается статистическая оценка результатов корреляционного анализа, т.е. рассчитываются отклонения фактических значений от рассчитанной по формуле величины. Практическое применение модели для прогнозирования и планирования величины показателя, так и для проведения факторного анализа, например: если у=5х1 + 10х2, то резерв Δу (Δх1) = 5 * Δх1

Анализ временных рядов Этот ряд зависит от спроса, а его анализ позволяет выявить закономерности спроса в течение года Сезонность- устойчивая закономерность внутригодичной динамики того или ингого явления. Временным рядом назовем последовательность значений одного и того же показателя, измеренного через определенные интервалы времени. Классический пример такого ряда – объемы продаж по месяцам.

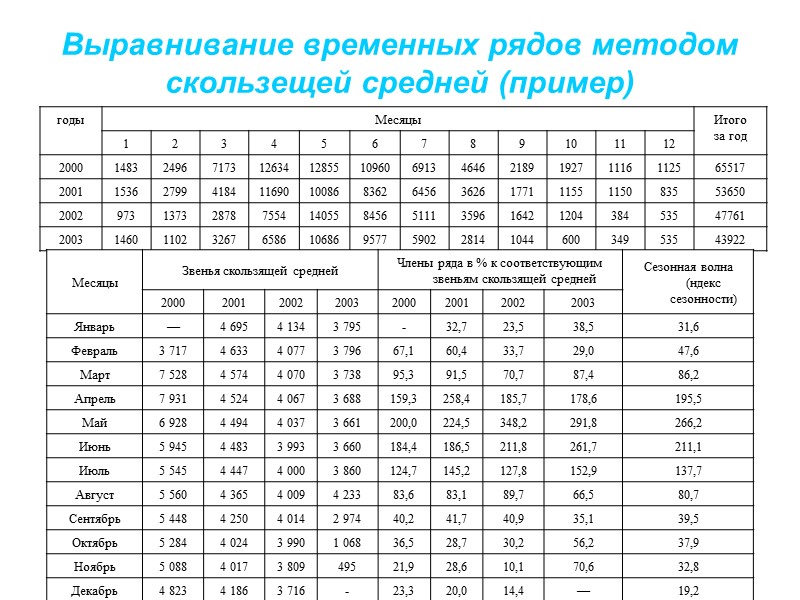
Тренд и сезонность Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая - это периодически повторяющаяся компонента. различие между двумя видами сезонности. Бывает: аддитивная (флуктуации не зависят от значений ряда Прогнозt=St + It-p ) мультипликативная (флуктуации не зависят от значений временного ряда Прогнозt = St*It-p) Оба эти вида регулярных компонент часто присутствуют в ряде одновременно Для выявления тренда и сезонности используют сглаживание (экспоненциальное, скользящей средней, ниаменьших квадратов)) и корреляционный анализ. По выровненному ряду определяют вид тренда, методами корреляционного анализа рассчитывают уравнение, характеризующее тренд. Средние по нескольким годам для данного периода процентные отклонения фактических занных от тренда отражают сезонные составляющие.