Математическая логика и теория алгоритмов Лекции Структура

Математическая логика и теория алгоритмов Лекции

Структура курса I. II. Математическая логика Раздел посвящен проблеме доказуемости математических утверждений (конец XIX-начало XX века, Давид Гильберт, Андрей Николаевич Колмогоров, Курт Гёдель и др. ) Теория алгоритмов и формальных языков Раздел посвящен проблеме вычислимости математических функций (XX век, Алан Тьюринг, Алонзо Черч, Эмиль Пост и др. ) 2

Изучаемые разделы математической логики 1. Теория булевых функций 2. Исчисление высказываний 3. Исчисление предикатов 3

1. Теория булевых функций Лекция 1

Понятие булевой переменной и булевой функции Определение Логической переменной (булевой переменной) называется переменная, которая принимает значения на булевом множестве B = {0, 1}. Определение Логической функцией (булевой функцией) от n переменных называется n-арная операция на булевом множестве B = {0, 1}. 5

Обозначение логических переменных и логических функций Для обозначения логических (булевых) переменных и функций принято использовать латинский алфавит: - строчные буквы; - строчные буквы с индексами. Примечание: традиционно для обозначения логических переменных используют буквы из конца алфавита (примеры: x, y, z, w, v, u, x 1, yi), а для обозначения булевых функций используют буквы из начала алфавита (примеры: f(x), g(x, y), h(x, y, z), f 1(x, y), gi(x)). 6

Способы задания логической функции n n Таблицы истинности Логические выражения 7

Понятие таблицы истинности Определение Таблицы истинности – таблица, в левой части которой перечислены в фиксированном порядке все 2 n наборов переменных (двоичных векторов длины n), а в правой части – значения функции на этих наборах. В таблице истинности наборы расположены в определённом порядке – лексикографическом, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа. 8

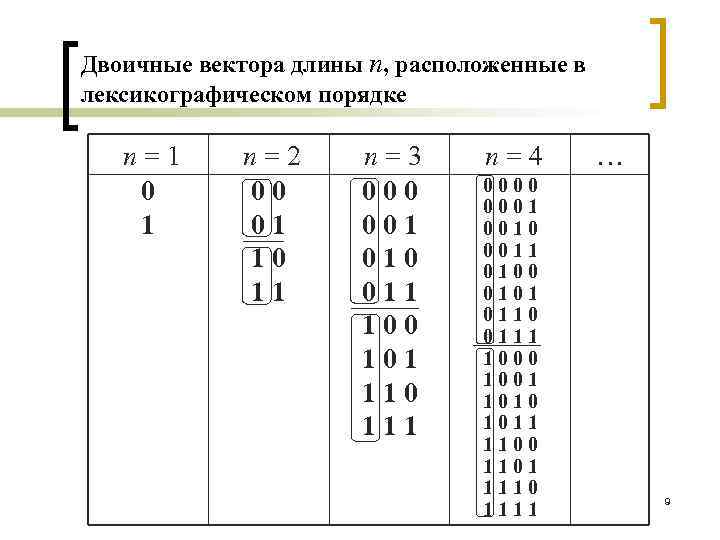Двоичные вектора длины n, расположенные в лексикографическом порядке n=1 0 1 n=2 00 01 10 11 n=3 000 001 010 011 100 101 110 111 n=4 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 … 9

Таблицы истинности логических функций от одной переменной Константа 0 Переменная x Отрицание x Константа 1 х 0 1 0 0 0 1 1 10

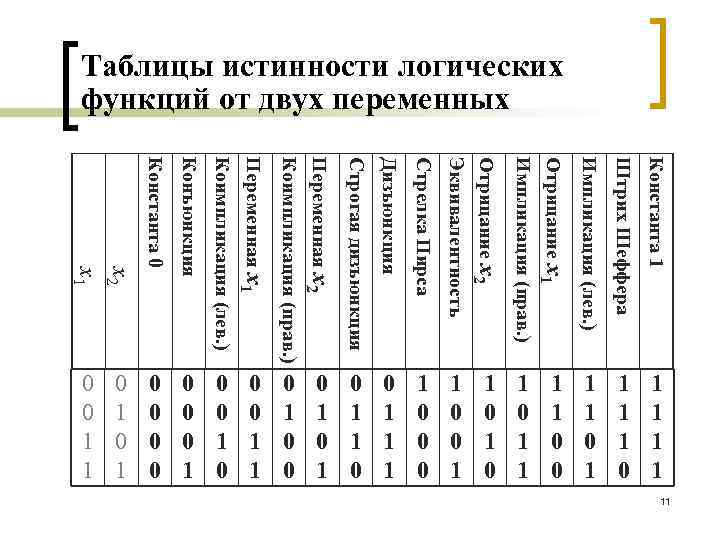Таблицы истинности логических функций от двух переменных Константа 0 Конъюнкция Коимпликация (лев. ) Переменная x 1 Коимпликация (прав. ) Переменная x 2 Строгая дизъюнкция Дизъюнкция Стрелка Пирса Эквивалентность Отрицание x 2 Импликация (прав. ) Отрицание x 1 Импликация (лев. ) Штрих Шеффера Константа 1 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 x 2 x 1 0 0 0 1 1 11

Число всех различных логических функций от n переменных Утверждение 1 Число всех возможных различающихся наборов значений n переменных логической функции f (x 1, x 2, . . . , xn) равно 2 n. □ Это число совпадает с числом всех возможных двоичных векторов длины n, следовательно, равно числу размещений с повторениями из 2 n. ■ Утверждение 2 Число всех различающихся n логических функций n переменных равно 22. □ Это число совпадает с числом всех возможных двоичных векторов длины 2 n, 12 n следовательно, равно 22. ■

Обозначение логических операций Для некоторых булевых функций существуют знаки операций: - булева функция от одной переменной (унарная операция): 1) отрицание: знак ¯ ( ), используют также знак ( х); - булевы функции от двух переменных (бинарные операции): 2) конъюнкция: знак ∙ (х∙у, ху), используют также знаки & (х&у) и (х у); 3) дизъюнкция: знак (х у); используют также знак + (х+у); 13

Обозначение логических операций 4) строгая дизъюнкция: знак (х у); 5) импликация: знак → (х→у), используют также знак (х у); 6) эквиваленция: знак (х у), используют также знак ↔ (х↔у); 7) штрих Шеффера: знак | (х|у); 8) стрелка Пирса: знак ↓ (х↓у). 14

Понятие логического выражения Определение 1) Логические переменные, символы 0 и 1 – логические выражения. 2) Если f – логическое выражение, то (f) и логические выражения. – 3) Если f, g – логические выражения, то fg, f→g, f~g, f ↓ g, f|g – логические выражения. 4) Других логических выражений нет. 15

Приоритет логических операций При вычислении значения логического выражения следует руководствоваться скобками и следующим приоритетом (старшинством) операций: 1) отрицание; 2) конъюнкция, штрих Шеффера, стрелка Пирса; 3) дизъюнкция, строгая дизъюнкция; 4) импликация; 5) эквиваленция. 16

Вычисление значений логических формул При вычислении значения логического выражения следует руководствоваться таблицами истинности логических операций. Пример 1 f(x, y) = x y (1) (2) (3) (4) (5) 0 0 1 1 1 0 1 1 0 0 0 1 0 1 1 17

Вычисление значений логических формул Пример 2 g(x, y, z) = x y z (1) (2) (3) (4) 0 0 0 1 0 0 1 0 1 0 1 1 0 0 1 1 0 0 1 1 0 0 0 18

Понятие несущественной (фиктивной) переменной Определение Переменная xi в функции f (x 1, x 2, . . . , xi 1, xi+1, . . . , xn) называется несущественной (фиктивной), если f (x 1, x 2, . . . , xi 1, 0, xi+1, . . . , xn) = f (x 1, x 2, . . . , xi 1, 1, xi+1, . . . , xn) при любых значениях остальных переменных, то есть, если изменение значения xi в любом наборе x 1, . . . , xn не меняет значения функции. ПРИМЕРЫ!!! 19

Понятие эквивалентных булевых функций Определение Две булевы функции f 1 и f 2 от n переменных называются эквивалентными, если на всех одинаковых наборах переменных (x 1, x 2, . . . , xn) они принимают одинаковые значения: f 1(x 1, x 2, . . . , xn) = f 2(x 1, x 2, . . . , xn). ПРИМЕРЫ!!! 20