84a6d10f06d780496f3ab8063d583179.ppt
- Количество слайдов: 24
 Matemáticas II Departamento de Economía Aplicada Universidad de La Laguna Proyecto: OPEN COURSE WARE 2012 Profesores que participan en el Proyecto: Marianela Carrillo Fernández Domingo Israel Cruz Báez Concepción González Concepción Juan Carlos Moreno Piquero Celina Pestano Gabino (Coordinadora) José Enrique Rodríguez Hernández
Matemáticas II Departamento de Economía Aplicada Universidad de La Laguna Proyecto: OPEN COURSE WARE 2012 Profesores que participan en el Proyecto: Marianela Carrillo Fernández Domingo Israel Cruz Báez Concepción González Concepción Juan Carlos Moreno Piquero Celina Pestano Gabino (Coordinadora) José Enrique Rodríguez Hernández
 Sistema de ecuaciones lineales x - 3 y + 4 z =-13 3 x - y + 2 z = -3 -3 x + 5 y - z = 9
Sistema de ecuaciones lineales x - 3 y + 4 z =-13 3 x - y + 2 z = -3 -3 x + 5 y - z = 9
 Resolver un sistema de ecuaciones lineales x - 3 y + 4 z =-13 3 x - y + 2 z = -3 -3 x + 5 y - z = 9 Forma de resolverlo: 1. Sistema tradicional 2. Mediante Álgebra Matricial
Resolver un sistema de ecuaciones lineales x - 3 y + 4 z =-13 3 x - y + 2 z = -3 -3 x + 5 y - z = 9 Forma de resolverlo: 1. Sistema tradicional 2. Mediante Álgebra Matricial
 2. Mediante Álgebra Matricial x - 3 y + 4 z =-13 3 x - y + 2 z = -3 -3 x + 5 y - z = 9 AX = B
2. Mediante Álgebra Matricial x - 3 y + 4 z =-13 3 x - y + 2 z = -3 -3 x + 5 y - z = 9 AX = B
 2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer
2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer
 2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer:
2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer:
 2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer:
2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer:
 2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer:
2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer:
 2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer 2. Método de Gauss A*=(A | B)
2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer 2. Método de Gauss A*=(A | B)
 2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer 2. Método de Gauss A*=(A | B)
2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer 2. Método de Gauss A*=(A | B)
 2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer 2. Método de Gauss A*=(A | B) 12 z = -24 z = -2 -4 y +11 z = -30 y = 2 x -3 y +4 z = -13 x = 1
2. Mediante Álgebra Matricial Si A es cuadrada y | A | 0 : 1. AX=B X=A-1 B Regla de Cramer 2. Método de Gauss A*=(A | B) 12 z = -24 z = -2 -4 y +11 z = -30 y = 2 x -3 y +4 z = -13 x = 1
 2. Mediante Álgebra Matricial En general, para cualquier A, con rango A=rango A*=h
2. Mediante Álgebra Matricial En general, para cualquier A, con rango A=rango A*=h
 ¿Cuándo un sistema de ecuaciones tiene solución?
¿Cuándo un sistema de ecuaciones tiene solución?
 ¿Cuándo un sistema de ecuaciones tiene solución? Si tiene solución, ¿Cuántas tiene?
¿Cuándo un sistema de ecuaciones tiene solución? Si tiene solución, ¿Cuántas tiene?
 Discutir las soluciones de un Sistema de Ecuaciones Lineales:
Discutir las soluciones de un Sistema de Ecuaciones Lineales:
 Discutir las soluciones de un Sistema de Ecuaciones Lineales: Th. Rouché-Frobenius Un sistema tendrá solución cuando: Si rango A = rango A* Si rango A* El sistema tiene solución El sistema no tiene solución Las soluciones serán: Si rango A = rango A* = n SCD (única solución) Si rango A = rango A* < n SCI (infinitas soluciones)
Discutir las soluciones de un Sistema de Ecuaciones Lineales: Th. Rouché-Frobenius Un sistema tendrá solución cuando: Si rango A = rango A* Si rango A* El sistema tiene solución El sistema no tiene solución Las soluciones serán: Si rango A = rango A* = n SCD (única solución) Si rango A = rango A* < n SCI (infinitas soluciones)
 Estudio por método de Gauss: rang A = rang A*=3 < n SCI (infinitas soluciones) rang A = rang A*=2 < n SCI (infinitas soluciones) rang A =2 rang A*=3 SI (no tiene solución)
Estudio por método de Gauss: rang A = rang A*=3 < n SCI (infinitas soluciones) rang A = rang A*=2 < n SCI (infinitas soluciones) rang A =2 rang A*=3 SI (no tiene solución)
 Ejemplos: Estudio por método de Gauss: rang A = rang A* si a, b 0 rang A = rang A*= 3 SCD si a =0 o b =0 rang A=2 SCI
Ejemplos: Estudio por método de Gauss: rang A = rang A* si a, b 0 rang A = rang A*= 3 SCD si a =0 o b =0 rang A=2 SCI
 Ejemplos: Estudio por método de Gauss: rang A = 2 b si a 0 rang A*= 3 SI si a =0 rang A*= 2 SCI
Ejemplos: Estudio por método de Gauss: rang A = 2 b si a 0 rang A*= 3 SI si a =0 rang A*= 2 SCI
 ¿Un sistema homogéneo tiene solución?
¿Un sistema homogéneo tiene solución?
 Sistema homogéneo: AX=0 rango A = rango A* El sistema tiene solución Si rango A = rango A* = n SCD (solución trivial)
Sistema homogéneo: AX=0 rango A = rango A* El sistema tiene solución Si rango A = rango A* = n SCD (solución trivial)
 Aplicación económica: Modelo Input-Output Ecuaciones que lo caracterizan: AX + D = X (I – A)X = D Si |I – A| 0 X = (I – A)-1 D Matriz inversa de Leontief
Aplicación económica: Modelo Input-Output Ecuaciones que lo caracterizan: AX + D = X (I – A)X = D Si |I – A| 0 X = (I – A)-1 D Matriz inversa de Leontief
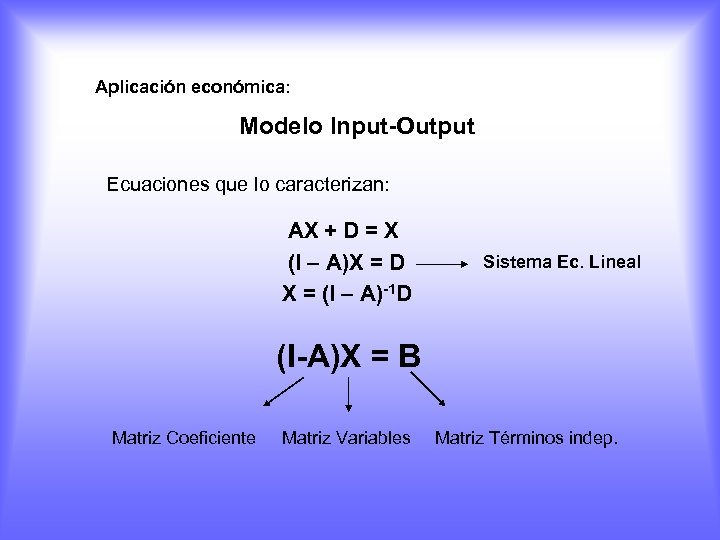 Aplicación económica: Modelo Input-Output Ecuaciones que lo caracterizan: AX + D = X (I – A)X = D X = (I – A)-1 D Sistema Ec. Lineal (I-A)X = B Matriz Coeficiente Matriz Variables Matriz Términos indep.
Aplicación económica: Modelo Input-Output Ecuaciones que lo caracterizan: AX + D = X (I – A)X = D X = (I – A)-1 D Sistema Ec. Lineal (I-A)X = B Matriz Coeficiente Matriz Variables Matriz Términos indep.
 Resumen sobre resolución de sistemas Un sistema de ecuaciones lineales: X=A-1 B AX = B |A| 0 Cramer Gauss A*=(A | D) Un modelo I/O: X=(I – A)-1 D (I – A)X = D |I-A| 0 Cramer Gauss A*=(I – A | D)
Resumen sobre resolución de sistemas Un sistema de ecuaciones lineales: X=A-1 B AX = B |A| 0 Cramer Gauss A*=(A | D) Un modelo I/O: X=(I – A)-1 D (I – A)X = D |I-A| 0 Cramer Gauss A*=(I – A | D)
