Логика высказываний Лекция 4 Формализация высказываний

Логика высказываний Лекция 4

Формализация высказываний ¡ Понятие о математической логике. Законы Аристотеля. ¡ Семантика логики высказываний. ¡ Синтаксис логики высказываний. ¡ ¡ Формулы логики высказываний и формализация высказываний. Интерпретации, разрешимость, выполнимость, общезначимость.

Понятие о математической логике. Законы Аристотеля Софизм – это преднамеренная ошибка, совершаемая с целью запутать оппонента и выдать ложное суждение за истину. ¡ Паралогизм – это непреднамеренная ошибка. ¡

Понятие о математической логике. Законы Аристотеля В формальной логике суждения расчленяются на субъект и предикат. ¡ В логике высказываний суждение рассматривается как простое, из которого с помощью логических операций строится сложное суждение. ¡

Понятие о математической логике. Законы Аристотеля ¡ ¡ ¡ Математическая логика – это символьная логика, она использует символы и операции. В этой логике каждому понятию соответствует свой символ. Характеристики: ¡ Использует язык и методы математики. ¡ Вызвана проблемами самой математики. Сегодня математическая логика используется в электронике, а также в системах с искусственным интеллектом. В основании математической логики используются законы Аристотеля

I закон тождества ¡ В процессе определенного рассуждения каждое понятие и суждение должно быть тождественно само себе. Х≡Х или Х Х

II закон противоречия Невозможно, что одно и то же, в одно и то же время, было и не было присуще одному и тому же в одном и том же отношении. ¡ (истина) ¡ ¡ (истина)

III закон исключенного третьего ¡ ¡ ¡ Равным образом не может быть ничего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо, чтобы то ни было, либо утверждать, либо отрицать. (истина) Часть логиков считают, что в ситуациях относительных к будущему закон исключенного третьего не применим.

Закон достаточного существования ¡ Всякая истинная мысль должна быть достаточно обоснована. Закон идемпотентности Х Х ≡Х Х Х≡Х

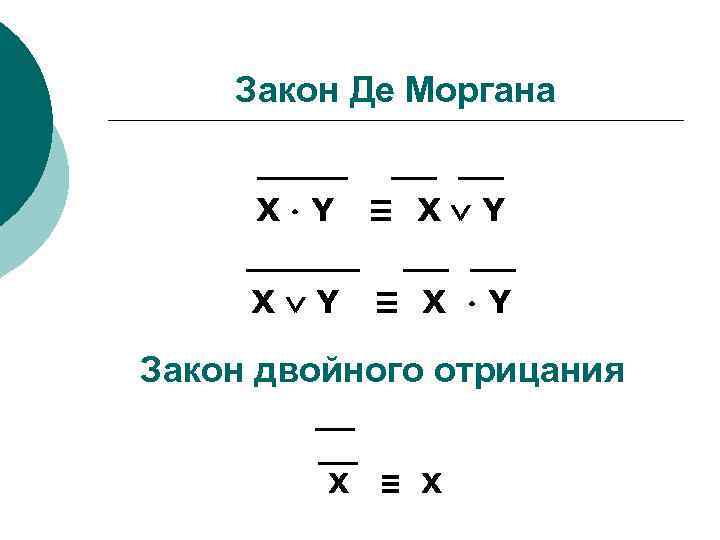Закон Де Моргана ____ __ __ Х Y ≡ X Y _____ __ __ Х Y ≡ X Y Закон двойного отрицания __ __ Х ≡ Х

Семантика логики высказываний ¡ ¡ В логике высказываний используется понятие “Высказывания”. Высказывание – это предложение, которое либо истинно, либо ложно. Высказывание как правило повествовательное предложение. Если нет общего мнения об истинности, то это не является высказыванием. Из двух и более высказываний строятся сложные высказывания, с помощью логических операций

¡ ¡ ¡ ¡ ¡ Конъюнкция: (логическое “и” “логическое умножение”). Обозначения: , , &. Дизъюнкция (логическое “или”, “логическое сложение”). Обозначения: и +. Импликация (“если…, то”, “когда, тогда”). Обозначения: , , . Эквиваленция (логическое “тогда и только тогда, когда”). Обозначения: , . Разделительное “или” (неравнозначность или “сумма по модулю 2”, или “исключающее или”). Обозначение: . ¡ ¡ ¡ Инверсия (логическое “не”, “неверно, что”). Унарная операция. Обозначения: , ┐.

¡ Особое внимание уделяется импликации, левый член называется антецедент, а правый –консеквент. __ Х Y=Х Y

¡ “Штрих Шеффера” и “Стрелка Пирса” – бинарные операции, с помощью которых могут быть выражены все другие операции. ¡ Штрих Шеффера (логическое “и-не”). Обозначение: |. ____ А|В≡А В ¡ Стрелка Пирса (логическое “или-не”). Обозначение: . ___ А В≡А В ¡ Символы логических операций называются пропозициональными знаками, а символы переменных – пропозициональными переменными.

Синтаксис логики высказываний. Формулы логики высказываний и формализация высказываний. ¡ Искусственные языки, создаваемые для нужд логики называются формализованным языками. При этом задается алфавит, где каждая последовательность символов называется словом. Затем вводится синтаксис – правила, позволяющие определять правильные слова, которые называются формулами.

Алфавит логики высказываний ¡ ¡ высказывательных или пропозициональных переменных (X, Y, Z, …. W) логических констант (0 – ложь, 1 - истина ) символы логических операций ( , |, , …) символы скобок ( [, ], {, }, (, ). )

Определение формулы Всякое высказывательная переменная – формула; ¡ Если F 1 и F 2 – формулы, то формулами являются F 1 F 2, … (т. е. при наличии знака операции между формулами). ¡ ¡ Всякий язык, служащий для объяснения другого языка, называется метаязык.

Формализация высказывания – это представления сложного высказывания формулой. В сложных высказываниях нужно выделить элементарные высказывания, знаки операций и представить это формулой. ¡ Пример: Если студент Зыков не присутствует на лекции и не является больным, то он находится в кино. __ __ [(Х Y) Z] где: Х – студент на лекции Y – студент болен Z – студент находится в кино

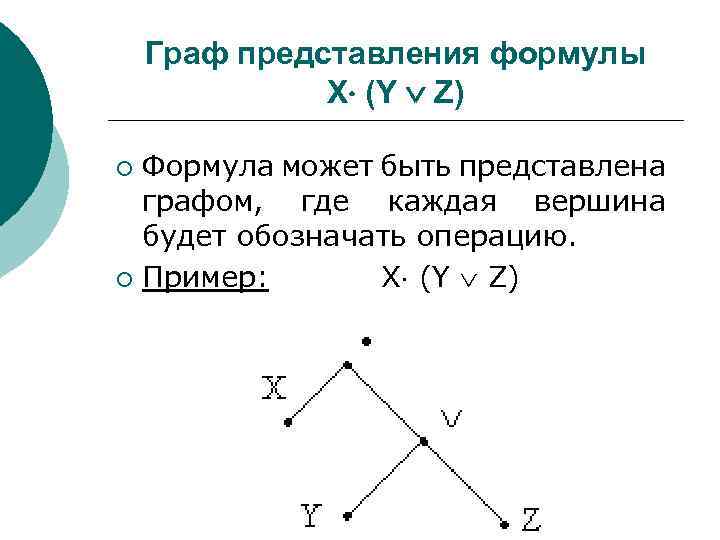Граф представления формулы X (Y Z) Формула может быть представлена графом, где каждая вершина будет обозначать операцию. ¡ Пример: X (Y Z) ¡

Интерпретации, разрешимость, выполнимость, общезначимость ¡ ¡ Интерпретация – это сопоставления каждому элементарному высказыванию некоторых значений истинности. Интерпретация, при которой значение формулы истинно называется моделью формулы. Формула называется выполнимой, если имеется ее модель, в противном случае формула является невыполнимой. __ __ [(Х Y) Z] 0 1 0 – модель формулы

¡ ¡ Формулы, которые всегда истинны или тождественно истинны, называются общезначимыми, или тавтологиями. Поиск этих формул – одна из основных задач логики. Для этого необходимо провести в общем случае 2 n проверок, где n – общее число пропозициональных переменных. Алгоритм проверки общезначимости для логики высказываний существует, поэтому логика высказываний разрешима, что нельзя сказать о логике предикатов.

Граф проверки общезначимости формулы ¡ Пример: проверка общезначимости ¡ [(Х Y Z) (Х Y)] (Х Z) где: Х, Y, Z – пропозициональные переменные Пусть Х = 1, тогда (Y Z) Y Z Пусть Х = 0, тогда формула обращается в 1 ¡ ¡ Доказательство общезначимости можно проводить путем приведения к абсурду, то есть доказательство от противного.