Логика предикатов Лекция 9
Принцип резолюции в логики предикатов Подстановка и унификация ¡ Резольвенция и факторизация ¡ Принцип резолюции ¡ Принцип логического программирования ¡
Подстановка и унификация Подстановка – это прием, в результате, которого из данных формул получают их частные случаи. ¡ {(t 1, x 1), (t 2, x 2), …, (tn, xn)} ¡ (ti, xi) – пара означающая, что всюду, где производится данная подстановка, переменная xi заменяется термом ti. ¡
Пример P(x, f(y), b) Подстановка: Θ 1 = {(z, x), (w, y)} Θ 2 = {(a, y)} PΘ 1 = P(z, f(w), b) PΘ 2 = P(x, f(a), b) ¡ Можно рассмотреть композицию подстановок, которая будет ассоциативной операцией. ¡
¡ ¡ Унификация: множество литералов {Li} называется унифицируемым, если существует такая подстановка, что L 1Θ = L 2Θ = … = LnΘ (они становятся одинаковыми). Подстановка Θ называется унификатором для множества литералов. Формулы, имеющие совместный частный случай, называются унифицируемыми, а набор подстановок – общим унификатором. Наименьший возможный унификатор называется Наиболее Общим Унификатором (НОУ)
Резольвенция и факторизация При доказательстве теорем в математической логике используют представление в виде дизъюнкции литералов (клаузальная форма, КНФ). ¡ Литерал L 1 называется дополнительным к литералу L 2, если: ¡
Резольвента двух предложений получается следующим образом: 1. 2. 3. 4. 5. Переменные одного предложения переименовываются так, чтобы они отличались от переменных другого предложения. Находится подстановка, при которой какой либо литерал одного предложения становится дополнительным к какому-либо литералу другого предложения и производится эта подстановка в оба предложения. Литералы, дополнительные другу вычёркиваются. Если имеются одинаковые литералы, то все они, кроме одного в каком либо предложении вычёркиваются (закон повторения). Дизъюнкция оставшихся литералов и есть резольвента.
Фактор какого-либо предложения – это следствие этого предложения, получаемое так: ¡ ¡ Находится подстановка, при которой какие либо литералы одинаковые. Выполняется эта подстановка, а все одинаковые литералы, кроме одного вычёркиваются. Дизъюнкция оставшихся литералов – фактор. Процесс нахождения факторов называется факторизацией.
Пример Резольвента:
Пример
Принцип резолюции ¡ ¡ Для доказательства невыполнимости множества предложений рассматривают метод построения семантического дерева, которое для невыполнимых предложений должно обрываться на какой либо вершине. Совокупность правил, используемых при получении следствий резольвент и факторов из заданных предложений, называется принципом резолюции.
Методом резолюции в логике предикатов будем доказывать логические следования некоторой формулы F из некоторого множества формул Фo. Доказывать будем от противного (то есть опровергать). ¡ Опровержение методом резолюций – это алгоритм автоматического доказательства теорем. ¡
¡ Каждая формула исходного множества и отрицания следствия представляется в виде множества предложений. В полученной совокупности предложений находятся резольвируемые предложения, и к ним применяется правило резолюции. Резольвента добавляется в соответствующее множество до тех пор, пока не будет получено пустое предложение.
При этом возможны три случая: ¡ ¡ ¡ В исходном множестве нет резольвированных предложений. Это значит, что теорема опровергнута. В результате очередного применения резолюции получаем пустое предложение. Теорема доказана. Процесс не заканчивается – множество предложений пополняется всё новыми резольвентами, среди которых нет пустых. Это ничего не означает.
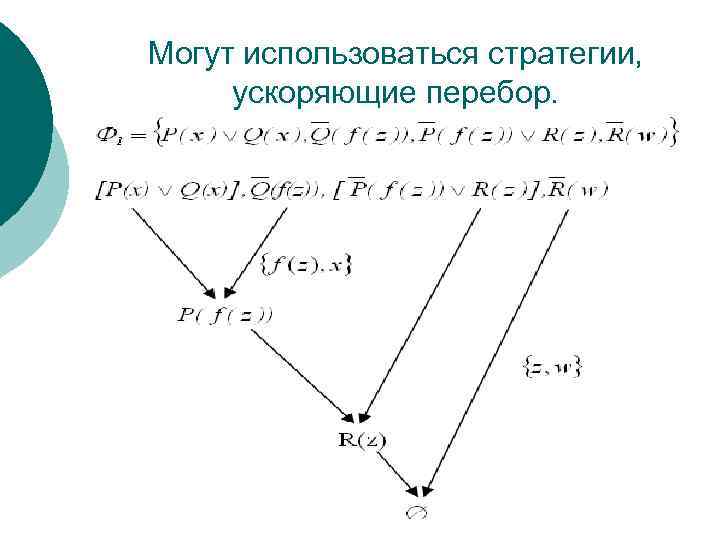Могут использоваться стратегии, ускоряющие перебор.
Принцип логического программирования ¡ Доказательство того, что формула следует из некоторого множества формул – это первый вариант задач логического программирования. Второй вариант – необходимость установить значения элемента x, при которых данная формула, содержащая в качестве одного из аргументов x, следует из Фo.
Пример Пусть погрузочный робот находится на автоматической тележке, которая находится на складе. Где находится погрузочный робот? ¡ Формулировка задачи в виде предикатов: ¡ «Быть в определённом месте» – Б(z, x), «z находится в x» ¡
¡ После построения дерева опровержения, для извлечения ответа строим модифицированное дерево доказательств следующим образом: ¡ Каждому предложению, вытекающему из отрицания предположения, добавляется в смысле дизъюнкции его отрицание. ¡ Выполняются те же самые резолюции, что и при построении дерева опровержения. ¡ В корне модифицированного дерева доказательства получается частный случай предположения, который используется в качестве ответа.
¡ Описанный процесс извлечения ответа можно применить при автоматическом построении простых программ.
¡ ¡ ¡ Пусть заданно некоторое отношение R(x, y), а также некоторые элементарные функции. Требуется написать программу, которая по заданной входной переменной “x” выдаёт значение “y”, удовлетворяющей этому отношению. При написании программы используются заданные элементарные функции. Требуемую программу можно построить путём процесса извлечения ответа, если будет доказано, что , удовлетворяющие этому отношению.