Логические основы построения компьютера Лекция № 4 Основные





















Lekcija_4,5_Logicheskie_osnovy_JeVM.ppt
- Количество слайдов: 35
 Логические основы построения компьютера Лекция № 4
Логические основы построения компьютера Лекция № 4
 Основные формы мышления Понятие Высказывание Умозаключение
Основные формы мышления Понятие Высказывание Умозаключение
 Основные операции алгебры логики Инверсия Конъюнкция Дизъюнкция Импликация Эквивалентность Неравнозначность
Основные операции алгебры логики Инверсия Конъюнкция Дизъюнкция Импликация Эквивалентность Неравнозначность
 Инверсия А или Таблица истинности инверсии
Инверсия А или Таблица истинности инверсии
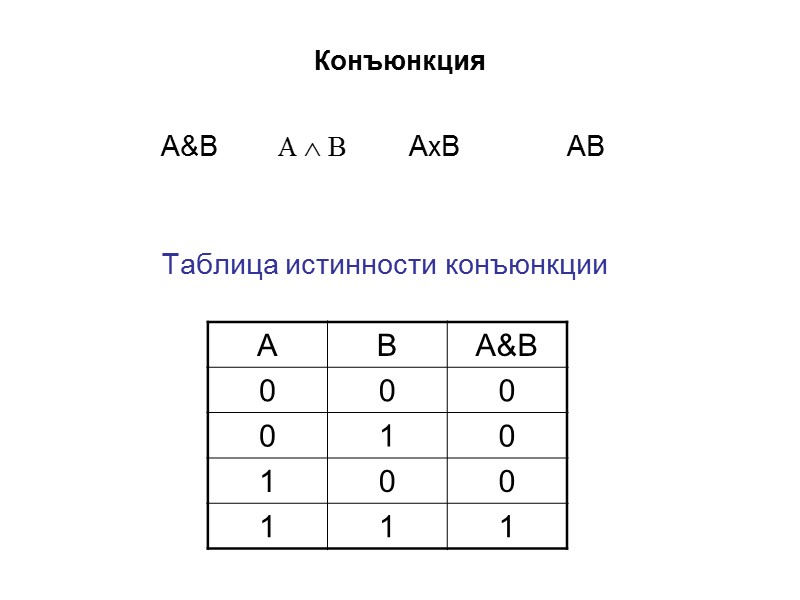
 Конъюнкция А&В АxВ АВ Таблица истинности конъюнкции
Конъюнкция А&В АxВ АВ Таблица истинности конъюнкции
 Дизъюнкция А+В Таблица истинности дизъюнкции
Дизъюнкция А+В Таблица истинности дизъюнкции
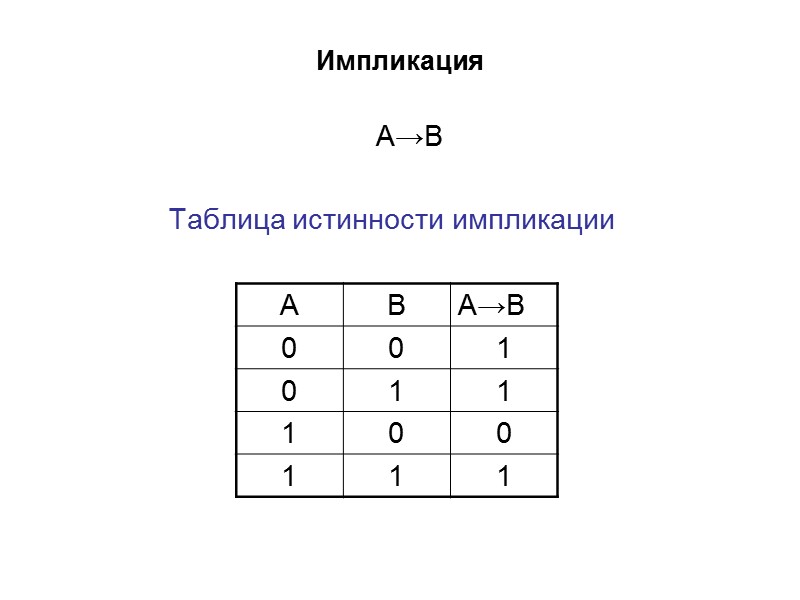
 Импликация А→В Таблица истинности импликации
Импликация А→В Таблица истинности импликации
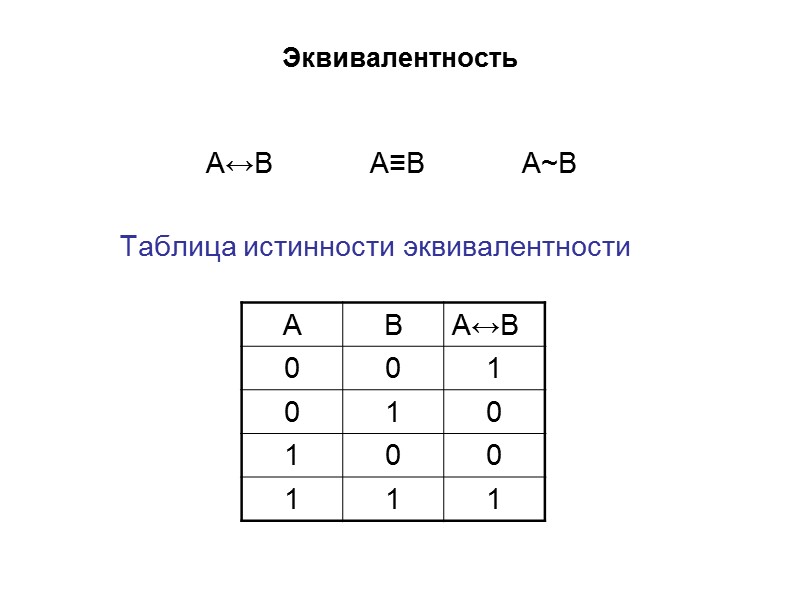
 Эквивалентность А↔В А≡В А~В Таблица истинности эквивалентности
Эквивалентность А↔В А≡В А~В Таблица истинности эквивалентности
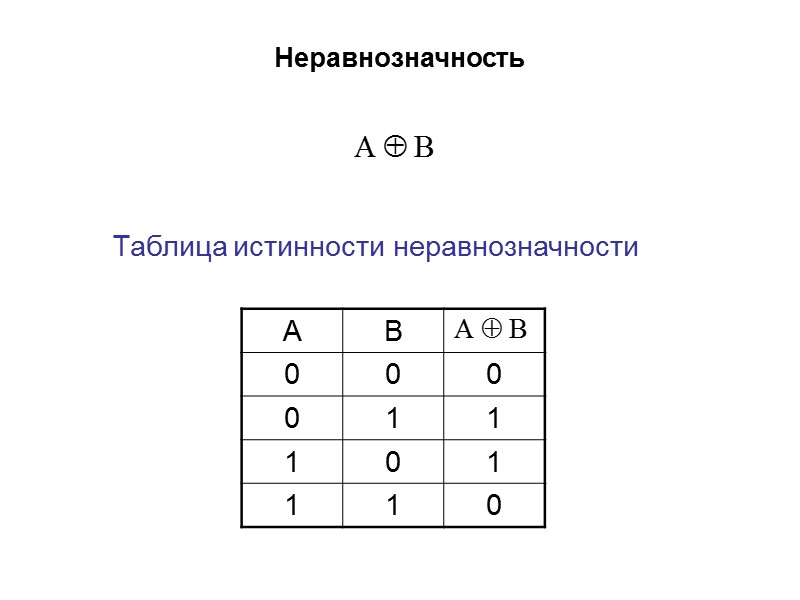
 Неравнозначность Таблица истинности неравнозначности
Неравнозначность Таблица истинности неравнозначности
 Примеры сложных логических выражений
Примеры сложных логических выражений
 Порядок выполнения логических операций 1) отрицание 2) конъюнкция 3) дизъюнкция 4) неравнозначность 5) эквивалентность 6) импликация
Порядок выполнения логических операций 1) отрицание 2) конъюнкция 3) дизъюнкция 4) неравнозначность 5) эквивалентность 6) импликация
 Вычислить значение выражения при a = 1, b = 2, c = 4. 1 2 3 4 5 6
Вычислить значение выражения при a = 1, b = 2, c = 4. 1 2 3 4 5 6
 Законы алгебры логики Закон идемпотентности А&А=А АνА=А Закон коммутативности АνВ= ВνА А&В= В&А Закон ассоциативности (AνB)νC=Aν(BνC) (A&B)&C=A&(B&C)
Законы алгебры логики Закон идемпотентности А&А=А АνА=А Закон коммутативности АνВ= ВνА А&В= В&А Закон ассоциативности (AνB)νC=Aν(BνC) (A&B)&C=A&(B&C)
 Законы алгебры логики Законы дистрибутивности Законы де Моргана Закон двойного отрицания
Законы алгебры логики Законы дистрибутивности Законы де Моргана Закон двойного отрицания
 Законы алгебры логики Закон исключения третьего Закон противоречия Действия с логическими константами
Законы алгебры логики Закон исключения третьего Закон противоречия Действия с логическими константами
 Формулы поглощения Формулы склеивания
Формулы поглощения Формулы склеивания
 Правила замены импликации эквивалентности неравнозначности
Правила замены импликации эквивалентности неравнозначности
 это замена их на равносильные на основе законов алгебры логики с целью получения выражения более простой формы. Упрощение сложных логических выражений = = Согласно правилам замены импликации и равнозначности применим закон поглощения для дизъюнкции
это замена их на равносильные на основе законов алгебры логики с целью получения выражения более простой формы. Упрощение сложных логических выражений = = Согласно правилам замены импликации и равнозначности применим закон поглощения для дизъюнкции
 Упрощение сложных логических выражений Применим закон де Моргана = На основании закона исключения третьего получаем результат = 1
Упрощение сложных логических выражений Применим закон де Моргана = На основании закона исключения третьего получаем результат = 1
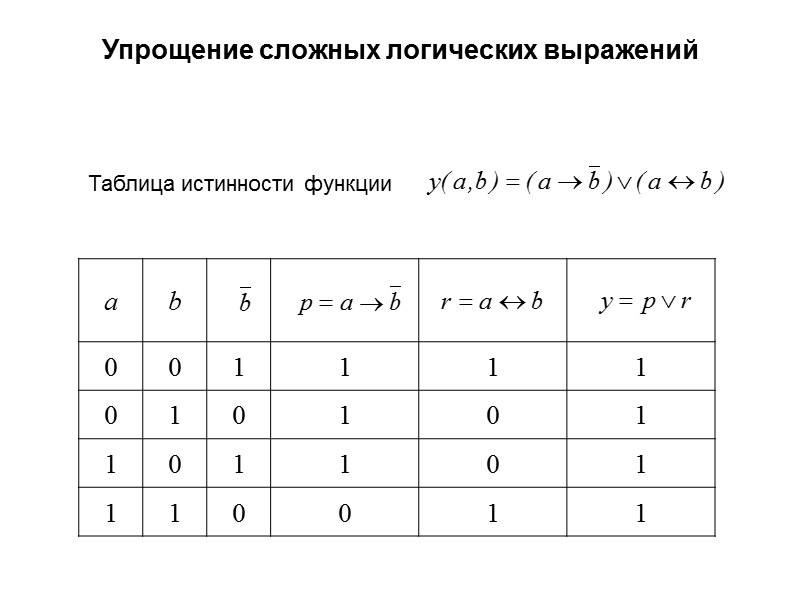
 Упрощение сложных логических выражений Таблица истинности функции
Упрощение сложных логических выражений Таблица истинности функции
 Логические основы построения компьютера (продолжение) Лекция № 4
Логические основы построения компьютера (продолжение) Лекция № 4
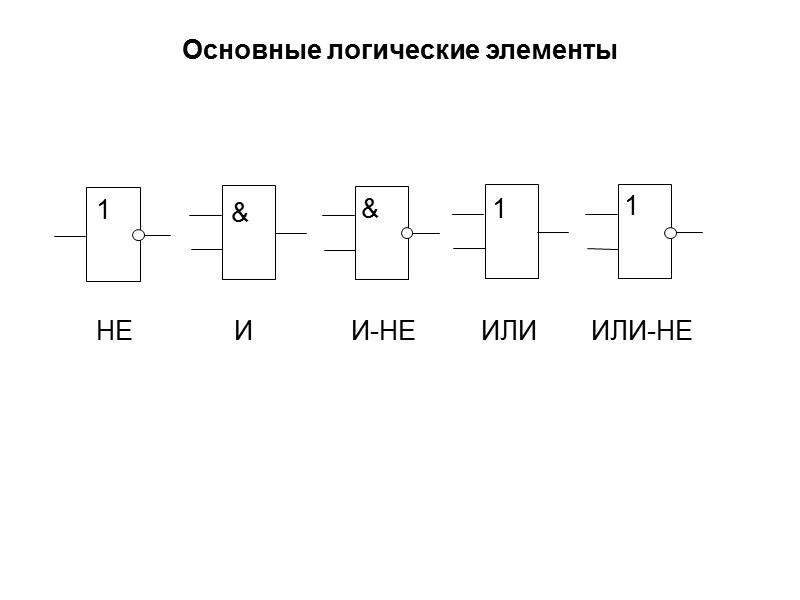
 Основные логические элементы НЕ И И-НЕ ИЛИ ИЛИ-НЕ
Основные логические элементы НЕ И И-НЕ ИЛИ ИЛИ-НЕ
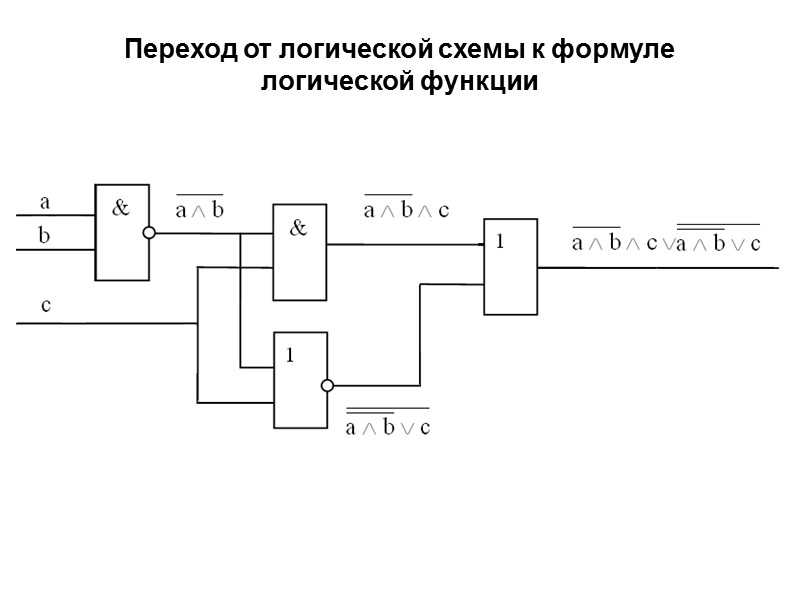
 Переход от логической схемы к формуле логической функции
Переход от логической схемы к формуле логической функции
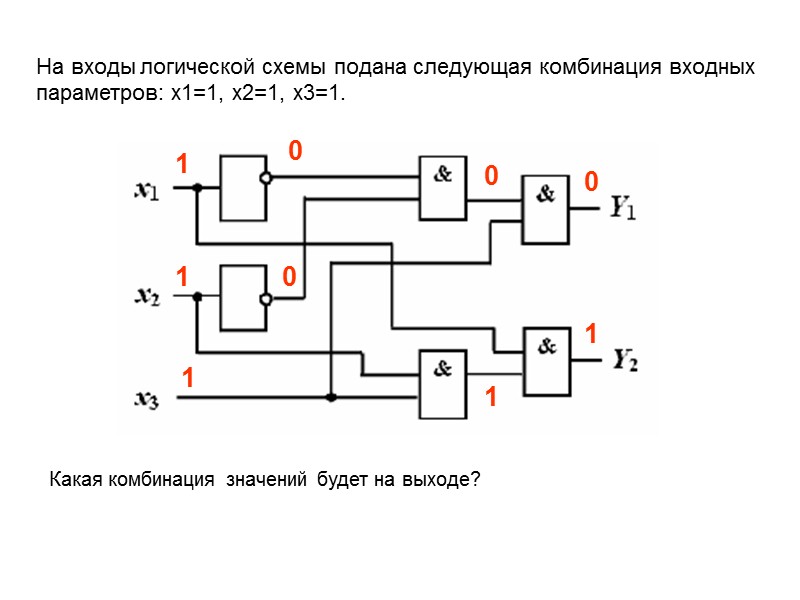
 На входы логической схемы подана следующая комбинация входных параметров: х1=1, х2=1, х3=1. Какая комбинация значений будет на выходе? 1 1 1 0 0 0 1 1 0
На входы логической схемы подана следующая комбинация входных параметров: х1=1, х2=1, х3=1. Какая комбинация значений будет на выходе? 1 1 1 0 0 0 1 1 0
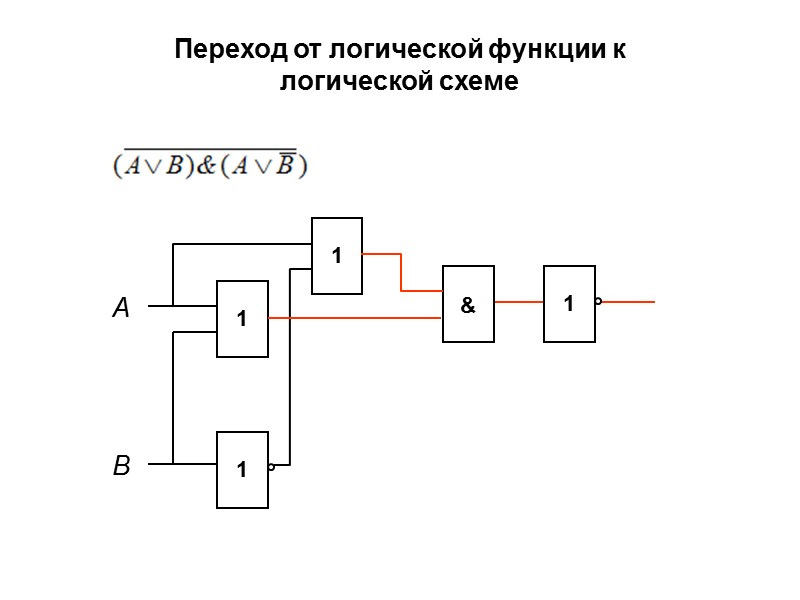
 Переход от логической функции к логической схеме А В 1 & 1
Переход от логической функции к логической схеме А В 1 & 1
 Составление логической схемы на основе таблицы истинности логической функции Совершенная дизъюнктивная нормальная форма (СДНФ) :
Составление логической схемы на основе таблицы истинности логической функции Совершенная дизъюнктивная нормальная форма (СДНФ) :
 Применяя законы исключенного третьего и исключения констант, имеем: Вынесем логический множитель y за скобки, а к скобочному выражению применим дистрибутивный закон: Применяя закон де Моргана имеем: Упростим полученное выражение:
Применяя законы исключенного третьего и исключения констант, имеем: Вынесем логический множитель y за скобки, а к скобочному выражению применим дистрибутивный закон: Применяя закон де Моргана имеем: Упростим полученное выражение:
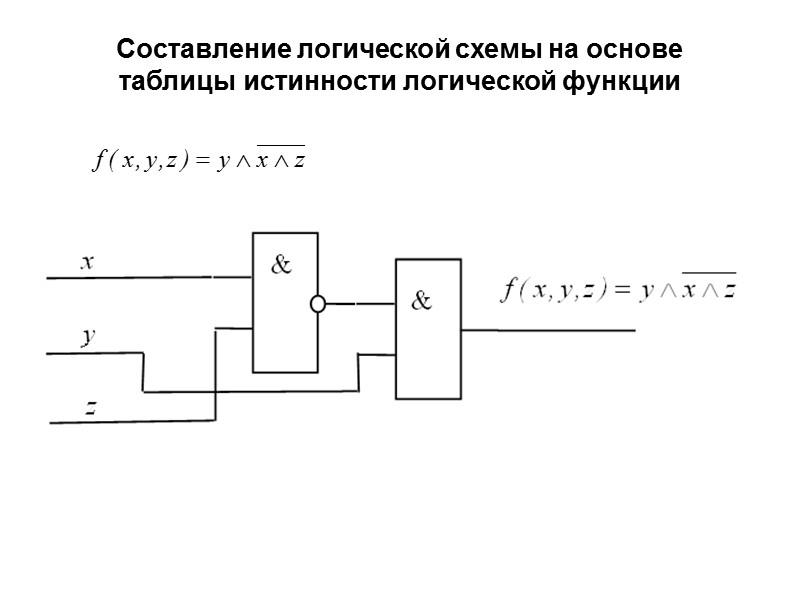
 Составление логической схемы на основе таблицы истинности логической функции
Составление логической схемы на основе таблицы истинности логической функции
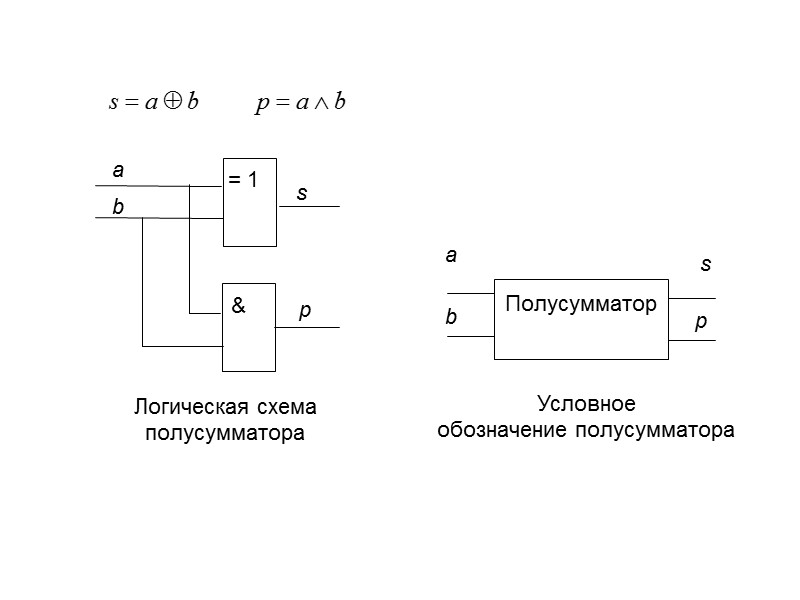
 Построить логическую схему полусумматора. Эта схема должна суммировать два одноразрядных двоичных числа и вырабатывать их сумму s и перенос в следующий разряд р. 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10 Таблица истинности полусумматора
Построить логическую схему полусумматора. Эта схема должна суммировать два одноразрядных двоичных числа и вырабатывать их сумму s и перенос в следующий разряд р. 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10 Таблица истинности полусумматора

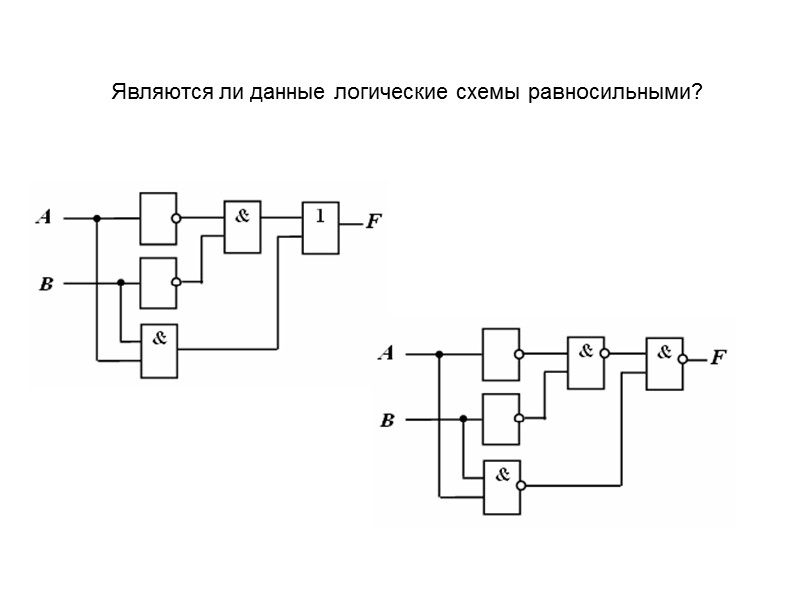
 Являются ли данные логические схемы равносильными?
Являются ли данные логические схемы равносильными?
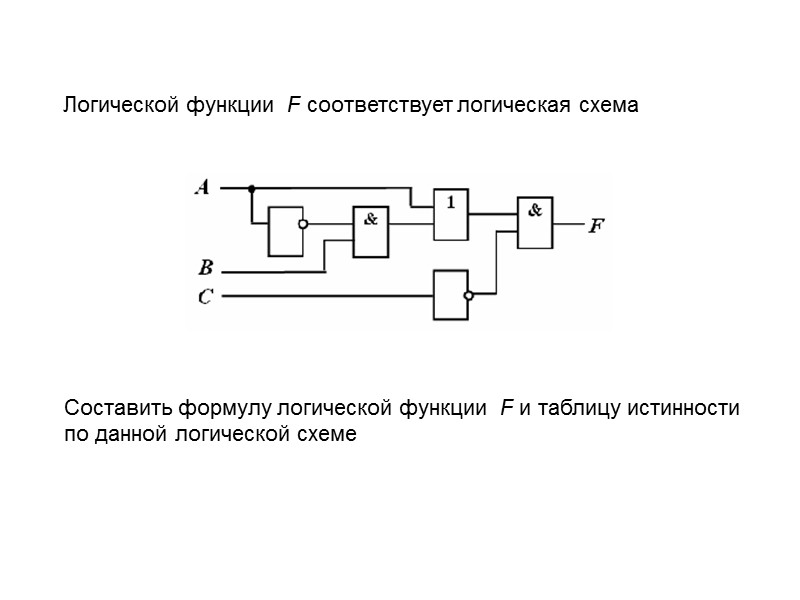
 Логической функции F соответствует логическая схема Составить формулу логической функции F и таблицу истинности по данной логической схеме
Логической функции F соответствует логическая схема Составить формулу логической функции F и таблицу истинности по данной логической схеме
 Решение текстовых логических задач Формальный способ решения логических задач предполагает несколько шагов: 1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами. 2. Записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций. 3. Составить единое логическое выражение для всех требований задачи (иногда единое выражение составлять не требуется). 4. Используя таблицы истинности логических операций, построить таблицу истинности для рассматриваемого выражения (или таблицы для отдельных сложных выражений). 5. Выбрать решение – набор значений простых высказываний, при котором построенное логическое выражение является истинным (или выполняется условие истинности отдельных сложных высказываний). 6. Проверить, удовлетворяет ли полученное решение условию задачи.
Решение текстовых логических задач Формальный способ решения логических задач предполагает несколько шагов: 1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами. 2. Записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций. 3. Составить единое логическое выражение для всех требований задачи (иногда единое выражение составлять не требуется). 4. Используя таблицы истинности логических операций, построить таблицу истинности для рассматриваемого выражения (или таблицы для отдельных сложных выражений). 5. Выбрать решение – набор значений простых высказываний, при котором построенное логическое выражение является истинным (или выполняется условие истинности отдельных сложных высказываний). 6. Проверить, удовлетворяет ли полученное решение условию задачи.
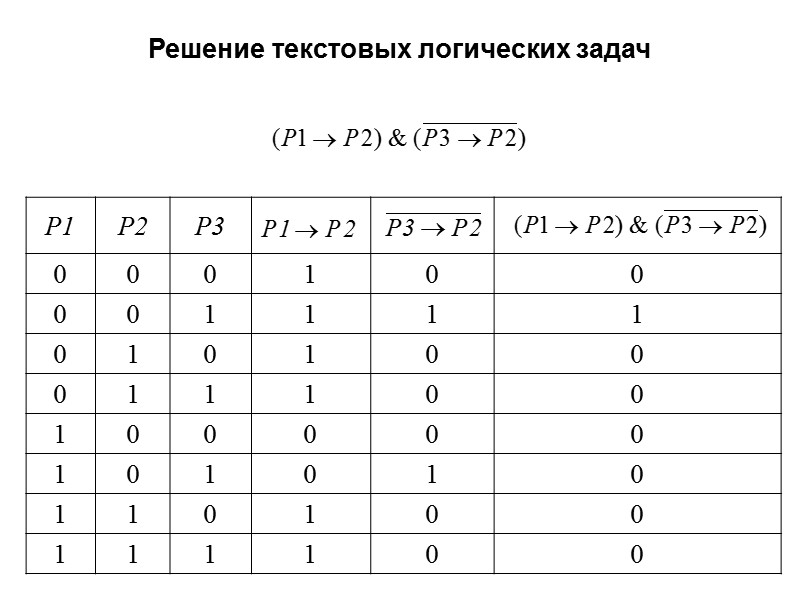
 На вопрос, кто из трех студентов изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из студентов изучал логику? Решение текстовых логических задач Простые высказывания Р1 - первый студент изучал логику Р2 - второй студент изучал логику Р3 - третий студент изучал логику
На вопрос, кто из трех студентов изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из студентов изучал логику? Решение текстовых логических задач Простые высказывания Р1 - первый студент изучал логику Р2 - второй студент изучал логику Р3 - третий студент изучал логику
 Решение текстовых логических задач
Решение текстовых логических задач
