Линейные системы и фильтрация Классификация систем Системы

Линейные системы и фильтрация

Классификация систем Системы, используемые для преобразования сигналов, имеют самые разнообразные физические характеристики и могут классифицироваться по различным признакам. Важнейшим классификационным признаком является линейность или нелинейность системы. Линейными называются системы, для которых выполняется принцип суперпозиции: реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности. Системы, для которых принцип суперпозиции не выполняется, называются нелинейными.

Импульсная характеристика линейных систем Пусть необходимо найти реакцию системы на любой входной сигнал, зная всего одну функцию — реакцию системы на поданную на вход дельта-функцию. Эта реакция называется импульсной характеристикой системы и обозначается Любой сигнал может быть представлен в виде свертки самого себя с дельта функцией

Импульсная характеристика Линейная система преобразует относительно переменной t все функции, входящие в это выражение. Входной сигнал при этом превращается в выходной сигнал , а дельта-функция в импульсную характеристику. В результате получается формула, показывающая, что выходной сигнал линейной системы с постоянными параметрами равен свертке выходного сигнала и импульсной характеристики системы:

Переходная характеристика Переходной характеристикой называют реакцию системы на поданную на вход функцию единичного скачка. Обозначается переходная характеристика как g(t). Поскольку дельта-функция — это производная от единичного скачка, импульсная и переходная характеристики связаны друг с другом операциями дифференцирования и интегрирования:

Комплексный коэффициент передачи Выходной сигнал линейной системы представляет собой свертку входного сигнала и импульсной характеристики. Преобразование Фурье от свертки дает произведение спектров сворачиваемых сигналов, так что в частотной области прохождение сигнала через линейную систему описывается очень просто: Здесь преобразование Фурье импульсной характеристики системы:

Комплексный коэффициент передачи Эта функция называется комплексным коэффициентом передачи системы, а ее модуль и фаза — соответственно амплитудно -частотной (АЧХ) и фазочастотной (ФЧХ) характеристиками Значение показывает, как изменяется при прохождении через систему комплексная амплитуда синусойды с частотой АЧХ показывает, во сколько раз изменится амплитуда синусоиды, а ФЧХ — каков будет полученный ею фазовый сдвиг.

Способы описания линейных систем Существуют различные эквивалентные способы представления характеристик линейных систем, реализуемых в виде цепей с сосредоточенными параметрами. Понимание сущности этих вариантов представления и способов перехода от одного представления к другому важно для правильного использования соответствующих функций МАТLАВ.

Дифференциальное уравнение Связь между входным и выходным сигналами линейной цепи с сосредоточенными параметрами может быть выражена в виде дифференциального уравнения (ДУ) вида:

Дифференциальное уравнение Здесь х(t) — входной сигнал, у(t) — выходной сигнал, аi, и bi — постоянные коэффициенты. Таким образом, цепь описывается наборами коэффициентов {а} и {b}. Должно выполняться неравенство , то есть максимальный порядок производной входного сигнала не может превышать максимального порядка производной выходного сигнала. Значение n называется порядком цепи.

Функция передачи Если применить к обеим частям ДУ преобразование Лапласа, получится выражение для операторного коэффициента передачи, или функции передачи цепи:

Преобразова ние Лапла са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Преобразование Лапласа Преобразованием Лапласа f(t) вещественной переменной , называется функция F(s) комплексной переменной s = σ + iω, такая что:

Функция передачи Преобразование Лапласа можно рассматривать как обобщение преобразования Фурье, при котором частота может принимать комплексные значения. Рассчитывается прямое преобразование Лапласа как Сравните эту формулу с формулой прямого преобразования Фурье.

Нули и полюсы Разложив числитель и знаменатель функции передачи на множители, мы получим функцию передачи в следующем виде: - коэффициент усиления - нули функции передачи - полюсы функции передачи В данном случае цепь описывается набором параметров

Нули и полюсы Нули функции передачи могут быть вещественными либо составлять комплексно-сопряженные пары. То же относится и к полюсам. Коэффициент усиления всегда вещественный.

Полюсы и вычеты Еще одним способом преобразования дробнорациональной функции передачи является ее представление в виде суммы простых дробей. При отсутствии кратных корней у знаменателя такое представление имеет следующий вид: Здесь рi, — полюсы функции передачи, а числа ri называются вычетами. С 0 целая часть функции передачи, отличная от нуля только в случае равенства степеней полиномов числителя и знаменателя. В данном случае цепь описывается набором параметров

Полюсы и вычеты Полюсы функции передачи могут быть вещественными либо составлять комплексно-сопряженные пары. Вычеты, соответствующие комплексносопряженным полюсам, также являются комплексно-сопряженными.

Расчет импульсной характеристики Представление функции передачи в виде суммы простых дробей позволяет вычислить импульсную характеристику системы, поскольку каждое слагаемое функции передачи вида: соответствует слагаемому импульсной характеристики вида

Устойчивость линейных систем Система называется устойчивой, если при нулевом входном сигнале выходной сигнал затухает при любых начальных условиях: Это требование равносильно требованию затухания импульсной характеристики:

Расчет частотных характеристик Для расчета комплексного коэффициента передачи необходимо подставить в функцию передачи мнимый аргумент: Соответствующие расчеты выполняются с помощью функции. В простейшем виде она имеет следующий синтаксис:

Расчет частотных характеристик Здесь b и а - векторы коэффициентов полиномов, соответственно числителя и знаменателя функции передачи. Коэффициенты следуют в порядке убывания степеней, заканчивая постоянным слагаемым. Для расчета характеристики по умолчанию выбирается 200 частот, логарифмически равномерно распределенных в диапазоне от 0, 1 до 10. При отсутствии выходных параметров функция строит графики АЧХ н ФЧХ. АЧХ выводится в логарифмическом масштабе ФЧХ — в градусах.

Расчет фильтров Одной из часто возникающих на практике задач является создание фильтров, пропускающих сигналы в определенной полосе частот и задерживающих остальные частоты. При этом различают: • фильтры нижних частот (ФНЧ), пропускающие частоты, меньшие некоторой частоты среза • фильтры верхних частот (ФВЧ, пропускающие частоты, большие некоторой частоты среза;

Полосовые и режекторные фильтры • полосовые фильтры пропускающие частоты в некотором диапазоне (они могут также характеризоваться средней частотой и шириной полосы пропускания • режекторные фильтры (другие возможные названия заграждающий фильтр, фильтрпробка, полосно-задерживающий фильтр, прогтускающие на выход все частоты, кроме лежащих в некотором диапазоне (они тоже могут характеризоваться средней частотой и шириной полосы задерживания.

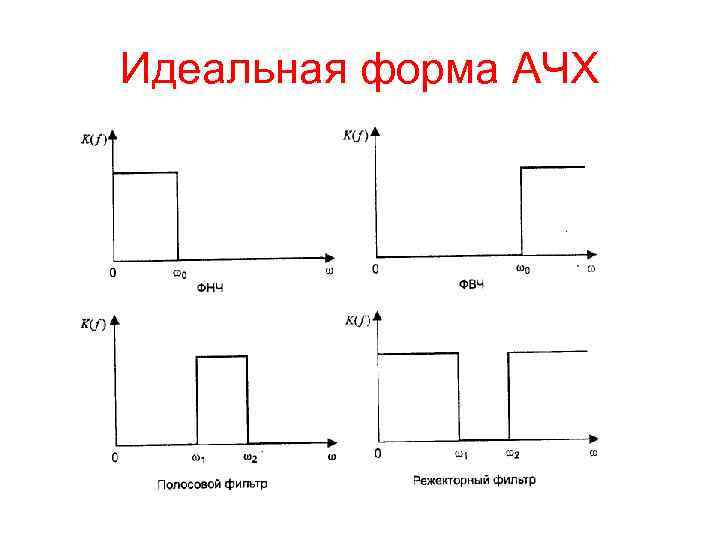Идеальная форма АЧХ

Идеальная форма АЧХ Однако такая идеальная (прямоугольная) форма АЧХ не может быть физически реализована. Поэтому в теории фильтров разработан ряд методов апроксимации прямоугольных АЧХ. Кроме того, рассчитан ФНЧ, можно несложными преобразованиями изменить его частоту среза, превратить его в ФВЧ, полосовой либо режекторный фильтр с заданными параметрами.

Фильтр Баттерворта • Функция передачи фильтра Баттерворта не имеет нулей а ее полюсы равномерно расположены на плоскости в левой половине окружности единичного радиуса • Благодаря такому размещению полюсов формула для АЧХ фильтра Баттерворта оказывается очень простой:

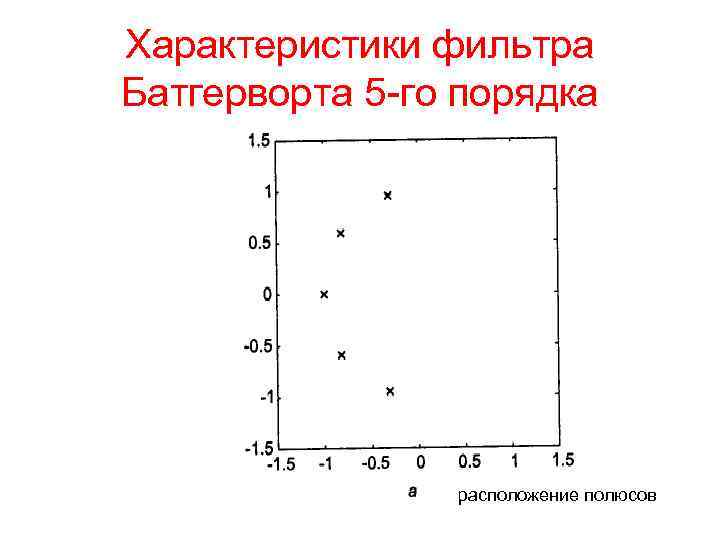Характеристики фильтра Батгерворта 5 -го порядка расположение полюсов

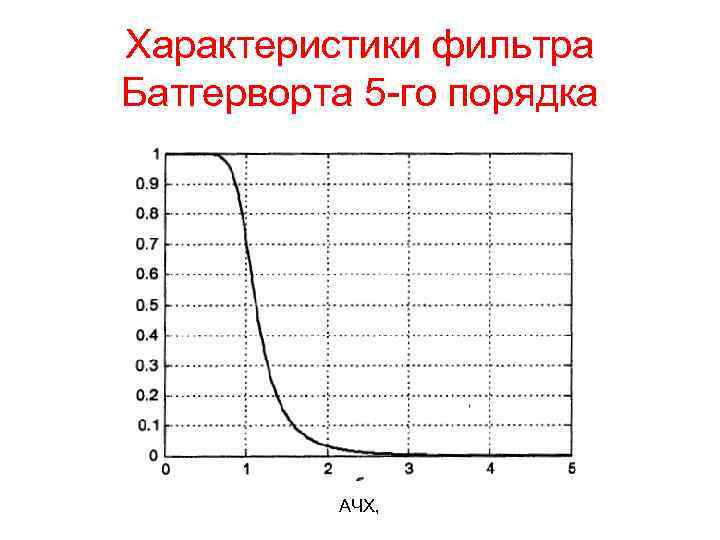Характеристики фильтра Батгерворта 5 -го порядка АЧХ,

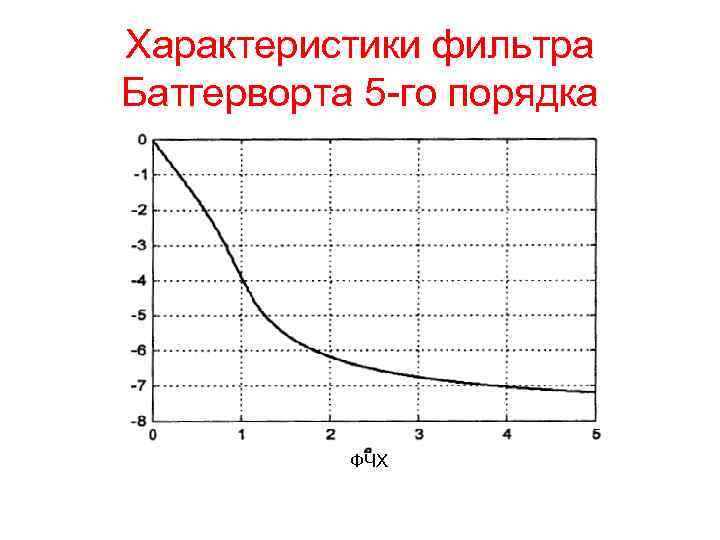Характеристики фильтра Батгерворта 5 -го порядка ФЧХ

Характеристики фильтра Батгерворта 5 -го порядка Коэффициент передачи на нулевой частоте равен 1, а на частоте среза независимо от порядка фильтра составляет При АЧХ стремится к нулю. АЧХ фильтра Баттерворта является максимально плоской при Это означает, что в данных точках равны нулю 2 n — 1 производных АЧХ по частоте. В целом АЧХ монотонно спадает от единицы до нуля при изменении частоты от нуля до бесконечности. В МАТIАВ расчет аналогового фильтра Баттерворта производится с помощью функции

Фильтр Чебышева первого рода Функция передачи фильтра Чебьтшева первого рода также не имеет нулей, а ее полюсы расположены в левой половине эллипса на s-плоскости АЧХ фильтра Чебышева первого рода описывается следующим образом:

Фильтр Чебышева первого рода Здесь ( — частота среза, Т(х) — полином Чебышева n-го порядка, n — порядок фильтра, — параметр, определяющий величину пульсаций АЧХ в полосе пропускания.

Фильтр Чебышева первого рода Функция передачи фильтра Чебышева первого рода также не имеет нулей, а ее полюсы расположены в левой половине эллипса на s-плоскости АЧХ фильтра Чебышева первого рода описывается следующим образом:

Фильтр Чебышева первого рода Здесь ( — частота среза, Т(х) — полином Чебышева n-го порядка, n — порядок фильтра, — параметр, определяющий величину пульсаций АЧХ в полосе пропускания.

Фильтр Чебышева первого рода Полином Чебышева колеблется в диапазоне -1. . . +1 а при неограниченно возрастает по абсолютной величине. Поэтому АЧХ фильтра Чебышева первого рода в полосе пропускания колеблется между значениями , , а вне полосы пропускания (при ‚ > монотонно затухает до нуля ( см рис. ) Коэффициент передачи на нулевой частоте равен 1 при нечетном порядке фильтра и при четном. На частоте среза коэффициент передачи фильтра равен т. е, то есть уровню пульсаций АЧХ в полосе пропускания.

Фильтр Чебышева первого рода По сравнению с фильтром Баттерворта того же порядка фильтр Чебышева обеспечивает более крутой спад АЧХ в области перехода от полосы пропускания к полосе задерживания.

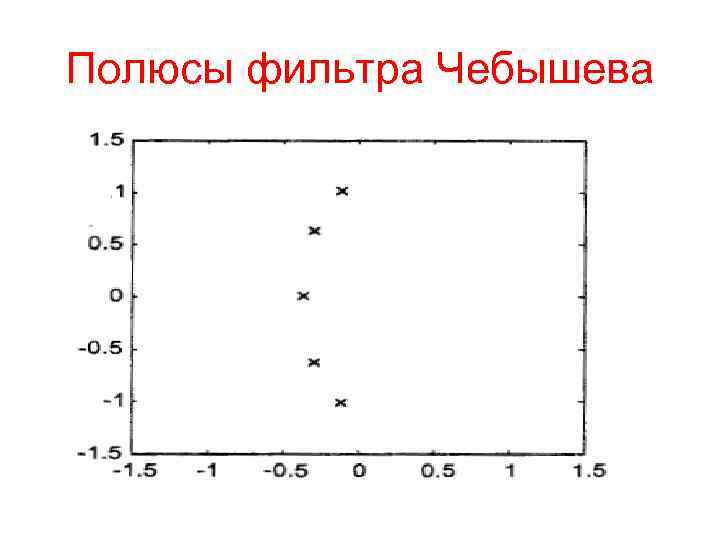Полюсы фильтра Чебышева

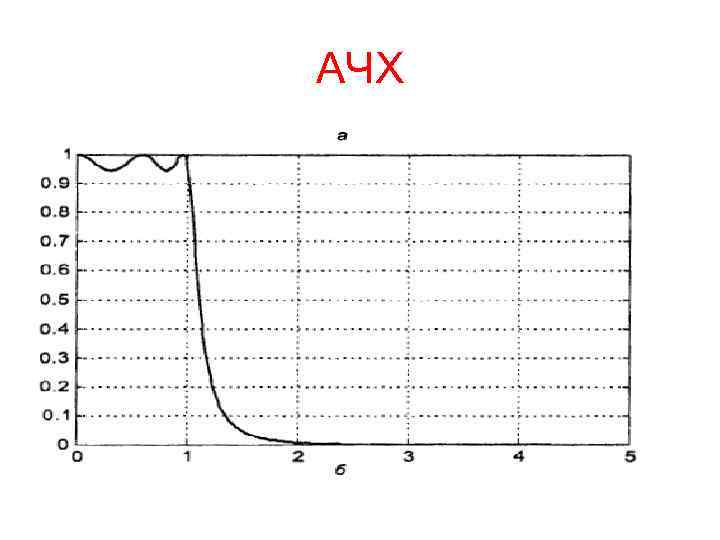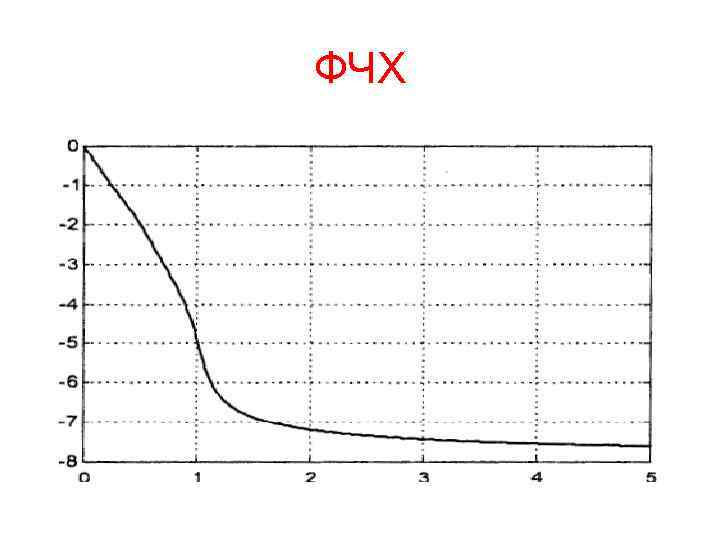АЧХ

ФЧХ

Эллиптический фильтр Эллиптичекие фильтры имеют пульсации заданной величины как в полосе пропускания, так и в полосе задерживания За счет этого удается обеспечить максимально возможную (при фиксированном порядке фильтра) крутизну спада АЧХ

Эллиптический фильтр (Фильтр Кауэра) — фильтр, характерной особенностью которого является пульсации амплитудно-частотной характеристики как в полосе пропускания, так и полосе подавления. Величина пульсаций в каждой из полос независима друг от друга. Другой отличительной особенностью такого фильтра является очень крутой спад амплитудной характеристики, поэтому с помощью этого фильтра можно достигать более эффективного разделения частот, чем с помощью других линейных фильтров.

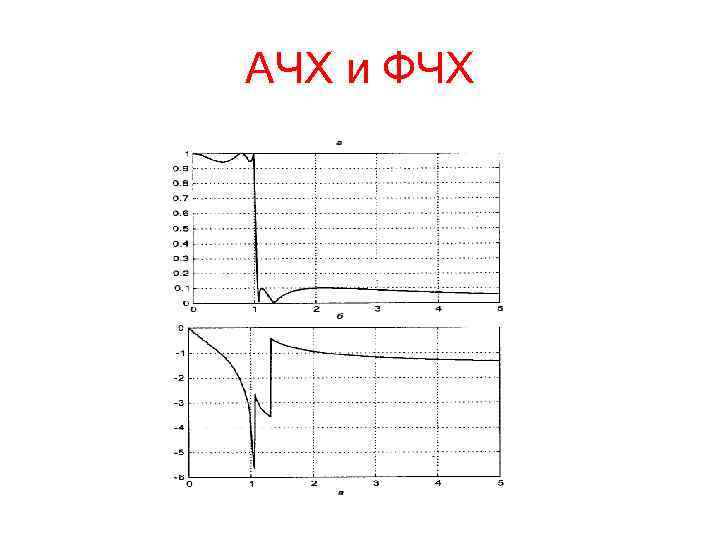АЧХ и ФЧХ

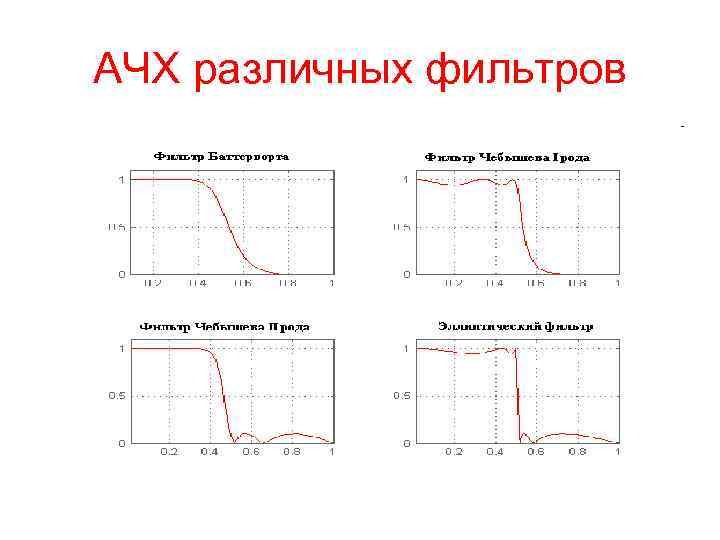АЧХ различных фильтров

Изменение частоты среза ФНЧ Изменение частоты среза ФНЧпрототипа сводится к простому масштабированию частотной оси и выполняется путем следуюoщей замены переменной s в выражении для функции передачи:

Расчет аналоговых фильтров Для расчета фильтра необходимо выполнить две основные операции: рассчитать ФНЧ-прототип и преобразовать его к нужному типу фильтра с заданными частотами среза. Требуемая последовательность действий оформлена в виде следующих функций МАТLАВ:

Дискретные и цифровые сигналы Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и т. д. ) преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в вычислительном устройстве.

Дискретное преобразование Лапласа Пусть решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени , где — целое число, а Т — период дискретизации. Тогда применяя преобразование Лапласа получим: Если применить следующую замену переменных: получим Z-преобразование:

Преобразование Лапласа для сигнала S(t) Воспользовавшись фильтрующим свойством дельта-функции Эта формула переходит в формулу определяющую z -преобразование, если выполнить подстановку:

Z-преобразование и преобразование Лапласа Выполняем подстановку: Таким образом, взаимное соответствие между z-преобразованием Х(z) и преобразованием Лапласа S(р) описывается следующим образом:

Связь Z-преобразования с преобразованием Фурье Похожими формулами описывается и связь z-преобразования Х(z) с преобразованием Фурье

Свойства z-преобразования линейность z-преобразование, является линейной комбинацией отсчетов последовательности, поэтому оно подчиняется принципу суперпозиции:

Свойства z-преобразования Задержка Если z-преобразование последовательности {х(k)} равно Х(z), то : -преобразование последовательности, задержанной на k 0 тактов будет иметь вид

Задержка Таким образом, при задержке последовательности на k 0 тактов необходимо умножить ее z- преобразование на : . Множитель является оператором задержки дискретной последовательности на тактов.

Свертка двух бесконечных дискретных последовательностей определяется следующим образом: Вычислим : z-преобразование для последовательности {у(k)}:

Свертка

Сущность линейной дискретной обработки Дискретный фильтр — это произвольная система обработки дискретного сигнала, обладающая свойствами линейности и стационарности. Под этими свойствами понимается то же, что и в аналоговом случае. Линейность означает, что выходная реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности, а стационарность — что задержка входного сигнала приводит лишь к такой же задержке выходного сигнала, не меняя его формы.

Фильтры с переменными параметрами Существуют и фильтры с переменными параметрами, не обладающие свойством стационарности. Это, например, адаптивные фильтры, меняющие свои параметры в зависимости от статистических свойств входного сигнала.

Память фильтра Любой фильтр обладает определенной частотной характеристикой. Чтобы она была нетривиальной, то есть чтобы коэффициент передачи фильтра на разных частотах был разным, выходной сигнал фильтра у(k) должен зависеть от нескольких отсчетов входного сигнала Х(k). Таким образом, дискретный фильтр должен обладать памятью.

Математические операции в фильтре Чтобы обеспечить линейность и стационарность, производимые фильтром математические операции должны ограничиваться сложением и умножением на константы.

Пример простейшего фильтра Пусть выходной сигнал фильтра равен сумме двух последних отсчетов входного сигнала: Убедимся в том, что эта система по-разному пропускает на выход сигналы разных частот. Для начала подадим на вход фильтра серию одинаковых отсчетов (то есть сигнал нулевой частоты):

Пример простейшего фильтра

Пример простейшего фильтра Как видим, уровень постоянного сигнала фильтр увеличил в два раза. Теперь подадим на вход отсчеты, одинаковые по модулю, но с чередующимися знаками (то есть отсчеты гармонического сигнала с частотой Найквиста):

Пример простейшего фильтра В отличие от постоянного сигнала, сигнал с частотой Найквиста на выход просто не прошел. Попробуем что-нибудь промежуточное, например сигнал с частотой, равной половине частоты Найквиста:

Пример простейшего фильтра

Пример простейшего фильтра На выходе в данном случае получаются отсчеты синусоиды, имеющей в раз большую амплитуду и некоторый фазовый сдвиг по сравнению со входным сигналом. Рассмотренный пример представляет собой простейший случай нерекурсивного фильтра. Такие фильтры суммируют некоторое число входных отсчетов, умножая их при этом на постоянные весовые коэффициенты.

Рекурсивные фильтры Теперь заметим, что помимо входных отсчетов мы можем использовать для вычислений и ранее рассчитанные значения выходного сигнала. Попробуем просто суммировать входной отсчет и предыдущий выходной отсчет:

Рекурсивные фильтры Подаем на вход постоянный сигнал (начальное состояние фильтра считаем нулевым):

Рекурсивные фильтры Так, очевидно, будет продолжаться и далее - выходной сигнал будет линейно нарастать, что рано или поздно приведет к переполнению разрядной сетки вычислительного устройства. Это сразу же демонстрирует нам главную отличительную черту фильтров, использующих при вычислениях предыдущие отсчеты выходного сигнала (их называют рекурсивными фильтрами) - из-за наличия обратных связей они могут быть неустойчивыми. Попробуем уменьшить влияние обратной связи, разделив предыдущий отсчет выходного сигнала на 2:

Рекурсивные фильтры Снова подаем на вход постоянный сигнал:

Рекурсивные фильтры Как видим, ситуация радикально изменилась - теперь выходной сигнал с уменьшающейся скоростью стремится к значению 2. Таким образом, переходный процесс в фильтре является бесконечным. Это еще одна отличительная черта рекурсивных фильтров.

Рекурсивные фильтры Итак, рекурсивные фильтры суммируют при расчетах не только входные, но и некоторое количество предыдущих выходных отсчетов сигнала, умножая их при этом на постоянные весовые коэффициенты. В общем случае дискретный фильтр суммирует (с весовыми коэффициентами) некоторое количество входных отсчетов (включая последний) и некоторое количество предыдущих выходных отсчетов:

Алгоритмом дискретной фильтрации Данная формула называется алгоритмом дискретной фильтрации. Если по другому сгруппировать слагаемые, чтобы с одной стороны от знака равенства были только входные отсчеты, а с другой - только выходные, получим форму записи, называемую разностным уравнением:

Разностное уравнение Структура разностного уравнения похожа на структуру дифференциального уравнения аналоговой линейной системы только вместо операции дифференцирования в формуле фигурируют задержки дискретных последовательностей. Как мы увидим далее, этим определяется и общность подходов к описанию аналоговых и дискретных систем. Однако весьма существенным является то, что в дискретной системе не существует каких-либо принципиальных ограничений на соотношение между количествами входных и выходных отсчетов, используемых при вычислениях.

Разностное уравнение m-ro порядка в общем случае имеет вид Форма уравнения подчеркивает итеративный характер разностного уравнения: если известны m предыдущих выходных значений y(n. Т - Т), y(n. Т— 2 Т) и т. д. и r+1 предыдущих входных значений х(n. Т), х(n. Т—Т) и т. д. , то можно вычислить новое выходное значение. Наглядное представление о выражении дает Рис

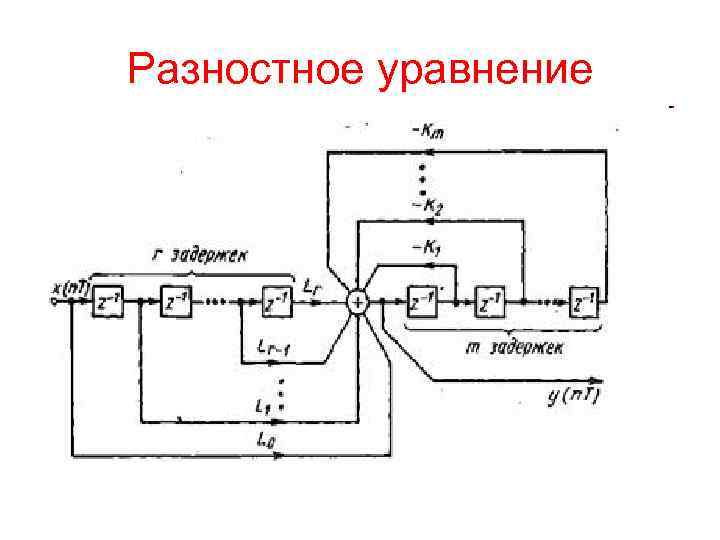Разностное уравнение

Импульсная характеристика В случае линейных систем с постоянными параметрами для анализа прохождения любого сигнала достаточно знать результат прохождения элементарного импульса в виде дельта-функции. Для дискретньгх систем также можно ввести в рассмотрение единичную импульсную функцию X 0(к) Выходная реакция на единичный импульс называется импульсной характеристикой дискретной системы и обозначается

Импульсная характеристика Как и в случае линейных систем с постоянными параметрами, знание импульсной характеристики позволяет проанализировать прохождение через дискретную систему любого сигнала. Прежде всего заметим, что произвольный сигнал {Х(k)} можно представить в виде линейной комбинации единичных отсчетов:

Дискретная свертка Выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик Выражение называется дискретной сверткой. Для физически реализуемой системы верхний предел суммирования в формуле можно заменить на к

Функция передачи Применим Z-преобразование к уравнению дискретной фильтрации Так как это уравнение представляет собой дискретную свертку, то, согласно свойствам : Zпреобразования результатом будет являться произведение : z-преобразований:

Функция передачи Функция равная отношению zпреобразований выходного и входного сигналов и представляющая собой zпреобразование импульсной характеристики системы, называется функцией передачи или системной функцией дискретной системы: