Лекция Дифференциальные уравнения Определение Дифференциальное уравнение — уравнение,

Лекция Дифференциальные уравнения

Определение Дифференциальное уравнение - уравнение, содержащее неизвестную функцию, аргументы и производные от неизвестных функций по этим аргументам. Определение Дифференциальные уравнения называются обыкновенными, если неизвестные функции зависят от одного аргумента, и уравнениями в частных производных, если неизвестные функции зависят от нескольких аргументов. Пример простейший пример ОДУ: y¢ = dy/dx; Замечание Особенность обыкновенных дифференциальных уравнений, все неизвестные должны быть функциями одного вещественного аргумента и все они и их производные должны входить в уравнение только в виде своих значений в одной и той же переменной .

Примеры нарушения этих требований неизвестная u — функция двух аргументов x и y; Это пример дифференциального уравнения в частных производных неизвестная функция и ее производная входят в уравнение в виде значений в разных точках t, t – 1 Это пример дифференциально-разностных уравнений 1. 2.

Дифференциальные уравнения первого порядка ОПРЕДЕЛЕНИЕ Обыкновенное дифференциальное уравнение (ОДУ)- уравнение, связывающее независимую переменную x, искомую функцию y = y(x) и ее производные y (x) , y (x) , … , y(n)(x) .  F(x, y , y  , y  , y  , … , y(n)) = 0 . ОПРЕДЕЛЕНИЕ Порядок старшей производной, входящей в ОДУ, называется порядком дифференциального уравнения. ПРИМЕР Определить порядок уравнений: Определение Дифференциальное уравнение 1 порядка имеет вид

Дифференциальное уравнение 1 порядка имеет вид или или или Замечание y ' = f (x, y) - такая форма дифференциального уравнения первого порядка называется нормальной, а уравнение является разрешимым относительно производной от искомой функции.

Определение Общим решением дифференциального уравнения называется такое его решение, содержащее произвольные постоянные, из которого любое частное решение может быть получено при соответствующем подборе произвольных постоянных. Определение Частное решение дифференциального уравнения — это решение, не содержащее произвольных постоянных. Определение Решение дифференциального уравнения, полученное в неявном виде F (x, y) = 0, называется интегралом дифференциального уравнения.

Определение Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Определение Дифференциальное уравнение называется интегрируемым в квадратурах, если все его решения могут быть получены в результате конечной последовательности элементарных действий над известными функциями и интегрированием этих функций. Определение Квадратура - операция взятия неопределенного интеграла.

Определение Функция y = (x) - решением дифференциального уравнения на интервале (a;b), если при ее подстановке в это уравнение получается тождество, справедливое для всех x из интервала (a;b). ПРИМЕР y = cos (x) – решение ДУ y  + y = 0 на (–  , + ) ; в интервале (– 1 ; 1) . Определение График решения (интеграла) дифференциального уравнения называется интегральной кривой. . Интегральные кривые для Решению соответствует некоторая кривая, которая называется интегральной кривой решение

Интегральные кривые Предположим, что в каждой точке некоторой области на плоскости выбрана проходящая через эту точку прямая. В таком случае говорят, что в области задано поле направлений ( или векторное поле). Определение Линия, которая в каждой своей точке касается имеющегося в этой точке направления поля, называется интегральной кривой поля направлений. Замечание Название " интегральные кривые" объясняется тем, что в некоторых случаях эти кривые можно найти при помощи операции интегрирования.

Геометрический смысл понятия поле направлений Уравнения (1) – направление касательной в каждой точке интегральной кривой совпадает с направлением поля в этой точке. Замечание Всякое дифференциальное уравнение 1 порядка выражает некоторое общее свойство касательных всех его интегральных кривых. Задача интегрирования состоит в том, чтобы по этому свойству восстановить само семейство интегральных кривых. Определение Кривая, в каждой точке которой наклон поля, определяемого дифференциальным уравнением (1), один и тот же, называется изоклиной этого уравнения (1) уравнение изоклин

Пример Решение В каждой точке, кроме начала координат, угловой коэффициент к искомой интегральной кривой равен то есть тангенсу угла, образованного с осью Ох прямой, проходящей через данную точку и начало координат. Следовательно, интегральными кривыми в данном случае будут прямые вида у = сх для построения интегральных кривых удобно найти геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами

Пример Изоклины уравнения задаются уравнениями так как на каждой изоклине производная должна сохранять постоянное значение. Полученные уравнения задают семейство концентрических окружностей с центром в начале координат, а угловой коэффициент касательной к интегральной кривой равен радиусу проходящей через данную точку окружности.

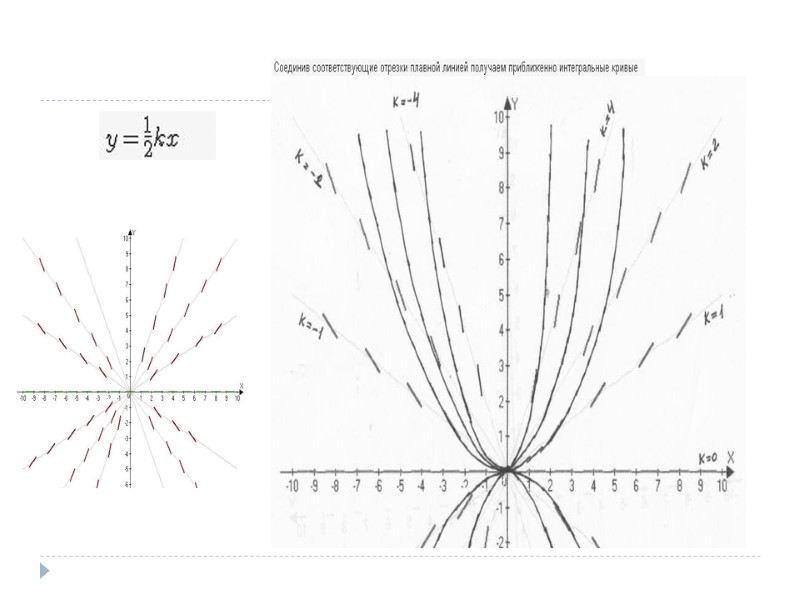
Пример С помощью изоклин начертить (приближенно) решение уравнения: xy' = 2y.

Теорема существования и единственности решения задачи Коши для уравнения y  = f(x,y) ТЕОРЕМА Пусть для уравнения y  = f(x,y) выполняются два условия: 1) f(x,y) непрерывна в некоторой области D плоскости xOy, 2) в области D ограничена. Тогда для любой точки M0(x0 ,y0)D существует единственное решение y = (x), определенное в некотором интервале (a;b), содержащем точку x0 , и удовлетворяющее условию y0 = (x0). Числа x0 , y0 называются начальными значениями (данными) для решения y = (x). Условие y(x0) = y0 называется начальным условием. Геометрически, задание начального условия означает, что на плоскости xOy задается точка (x0,y0) , через которую проходит интегральная кривая y(x).

Задача нахождения решения дифференциального уравнения F(x, y, y )=0, удовлетворяющего начальному условию y(x0) = y0, называется задачей Коши. Определение Решение (интеграл), в каждой точке которого выполняется условие единственности, называется частным. Определение Решение (интеграл) y = (x), в каждой точке которого нарушено условие единственности (т.е. через каждую точку кривой y = (x) проходит еще хотя бы одна, отличная от y = (x), интегральная кривая), называется особым. Задача Коши

Основные вопросы, которые связаны с задачей Коши Существует ли (хотя бы локально) решение задачи Коши? Если решение существует, то какова область его существования? Является ли решение единственным? Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?

Замечание. Теорема дает достаточные условия существования и единственности решения задачи Коши.  Возможно, что в точке (x0,y0) условия теоремы не вы- полняются, а решение y = y(x) уравнения, удовлетворяющее условию y(x0) = y0, существует и единственно. Из теоремы следует  1) вся область D покрыта интегральными кривыми уравнения , которые нигде между собой не пересекаются; 2) ДУ имеет множество решений. 3) Совокупность решений зависит от произвольной постоянной.

ОПРЕДЕЛЕНИЕ. Общим решением дифференциального урав нения y  = f(x,y) в области D существования и единствен- ности решения задачи Коши называется функция y = (x , C) , зависящая от x и одной произвольной постоянной C, которая удовлетворяет следующим двум условиям: 1) при любом допустимом значении постоянной С она удовлетворяет уравнению (2); 2) каково бы ни было начальное условие y(x0) = y0 (где (x0 ,y0)D), можно найти единственное значение C = C0 такое, что функция y = (x , C0) удовлетворяет данному начальному условию. Уравнение Φ(x , y , C) = 0 , задающее общее решение в неявном виде, называется общим интегралом уравнения.

Любое решение (интеграл), получающееся из общего решения (интеграла) при конкретном значении постоянной C (включая C = ), является частным. Особое решение, очевидно, не входит в общее решение дифференциального уравнения. Особое решение всегда «теряется» в процессе интегрирования и обладает тем свойством, что оно может быть включено в общее решение, если допустить C = C(x) . С геометрической точки зрения особая интегральная кривая является огибающей семейства интегральных кривых. ОПРЕДЕЛЕНИЕ. Линия ℓ называется огибающей однопара- метрического семейства кривых, если она в каждой своей точке касается одной кривой семейства, причем в различных точках она касается различных кривых.

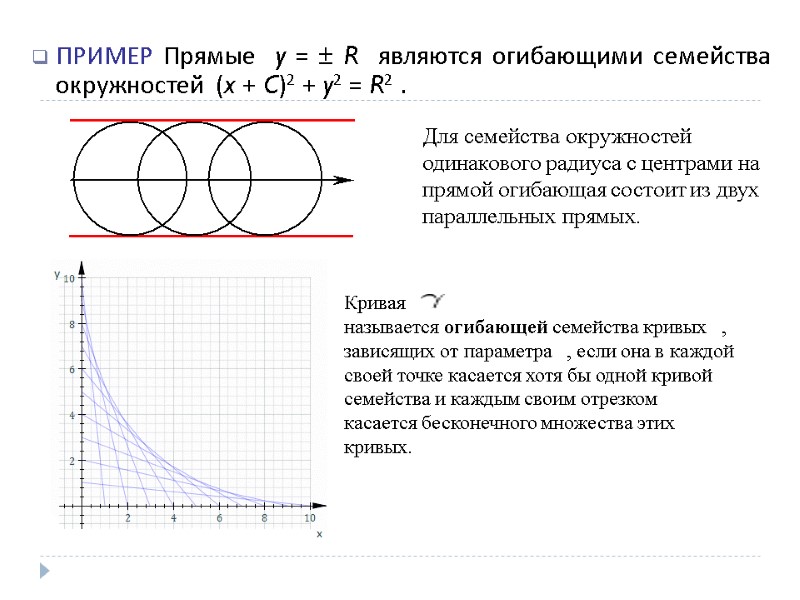
ПРИМЕР Прямые y =  R являются огибающими семейства окружностей (x + C)2 + y2 = R2 . Кривая называется огибающей семейства кривых , зависящих от параметра , если она в каждой своей точке касается хотя бы одной кривой семейства и каждым своим отрезком касается бесконечного множества этих кривых. Для семейства окружностей одинакового радиуса с центрами на прямой огибающая состоит из двух параллельных прямых.

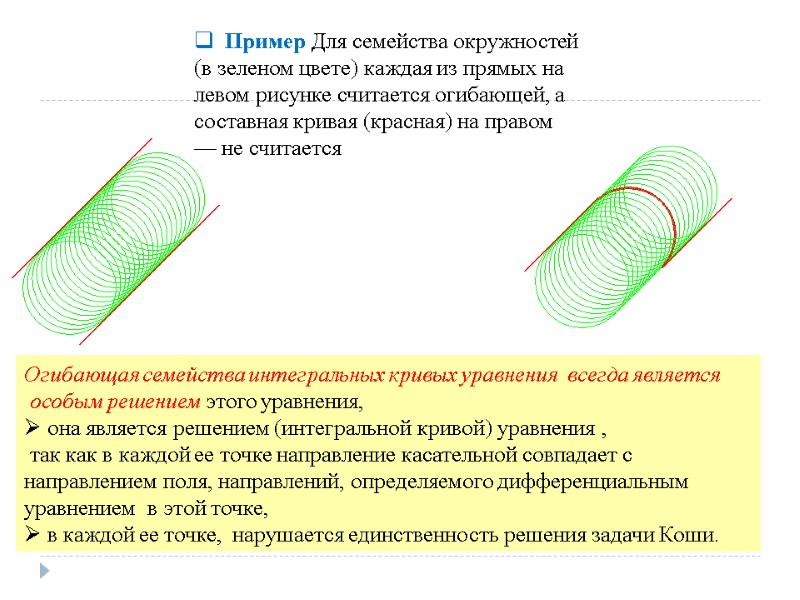
Пример Для семейства окружностей (в зеленом цвете) каждая из прямых на левом рисунке считается огибающей, а составная кривая (красная) на правом — не считается Огибающая семейства интегральных кривых уравнения всегда является особым решением этого уравнения, она является решением (интегральной кривой) уравнения , так как в каждой ее точке направление касательной совпадает с направлением поля, направлений, определяемого дифференциальным уравнением в этой точке, в каждой ее точке, нарушается единственность решения задачи Коши.

Уравнения с разделяющимися переменными Уравнения с разделяющимися переменными являются одним из основных типов уравнений 1 порядка, разрешенных относительно производной и допускающих интегрирование в квадратурах. Многие дифференциальные уравнения приводятся к уравнению с разделяющимися переменными при соответствующей замене искомой функции и независимой переменной. Определение Дифференциальное уравнение вида: называют уравнением с разделенными переменными

Решение дифференциального уравнения с разделенными переменными уравнение с разделенными переменными Интегрируем общий интеграл уравнения (1). Особых решений нет. (1) Замечание можно не писать пределов интегрирования, ибо числа, получающиеся от подстановки нижних пределов можно включить в произвольную постоянную

Замечание. В теории дифференциальных уравнений символом принято обозначать ОДНУ из первообразных функции f(x) (а не все множество первообразных, как это принято в других разделах математического анализа). Поэтому общий интеграл уравнения принято записывать в виде: где C – произвольная постоянная.

Уравнения с разделяющимися переменными Определение Дифференциальное уравнение с разделяющимися переменными -уравнение, дифференциальная форма которого имеет вид f1(x)  1(y)dx + f2(x)  2(y)dy = 0 , где f1(x), f2(x), 1(y), 2(y) – непрерывные функции. Разделим обе части уравнения на 1(y)  f2(x):  Общий интеграл уравнения имеет вид:

Замечания 1) Деление на 1(y)  f2(x) может привести к потере решений. Поэтому чтобы получить полное решение, необходимо рассмотреть корни уравнений 1(y) = 0, f2(x) = 0. 2) Обычная форма дифференциального уравнения с разделяющимися переменными имеет вид: y  = f(x)  (y) . Рассмотрим уравнение y  = f(ax + by + c) , где a , b и c – некоторые числа. Оно приводится к уравнению с разделяющимися переменными заменой z(x) = ax + by + c и его общий интеграл имеет вид:

Пример Решить уравнение и выделить интегральную кривую, проходящую через точку (0,1) Решение Разделяя переменные, имеем отсюда следует, что - общий интеграл Все решения - особые, т.к. не получаются из формулы общего интеграла ни при каких значениях произвольной постоянной и на каждом из них нарушается единственность задачи Коши

Полагая находим или решение задачи Коши в виде Но через точку проходит и особое решение получаем две интегральные кривые, проходящие через точку