Лекция 6 ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ = ,

Лекция 6 ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ

= , 2 2 A A A(Δ x ) (Δ y ) = , Ax A A Δ arc tg Δy 1. Понятие о перемещениях При воздействии нагрузки, температуры и других факторов сооружения меняют свою форму, а его точки получают перемещения: Перемещение любой точки А на плоскости можно задать через его модуль A и направление A , которые определяются по формулам: где x A и y A − горизонтальная и вертикальная составляющие A. Перемещение – векторная величина :

Методы определения перемещений основаны на вычислении работ внешних и внутренних сил. 2. Действительные работы внешних и внутренних сил. Потенциальная энергия Действительным перемещением называется перемещение, вызванное силой по направлению ее действия. В упругих системах перемещение прямо пропорционально действующей силе, и в них выполняется закон Гука = P. где − податливость. Эту зависимость представим в виде: Диаграмма −P

Сила на действительном перемещении выполняет некоторую работу. В механике ее называют действительной работой. Действительная работа силы P определяется по диаграмме −P : . P 01 W d. W P 2 Теорема Клапейрона : Сила, действующая на упругую систему, совершает работу, равную половине произведения силы на перемещение. Если воспользоваться законом Гука, то Значит, внешняя сила совершает положительную работу. Когда действуют несколько сил, то по принципу суперпозиции . 21 W P 0 2 . kk 1 W PΔ

В идеально-упругой системе работа внешних сил W полностью переходит в потенциальную энергию деформации U : W =U. Если убрать внешние силы, упругая система возвратится в исходное положение. Эту работу совершают внутренние силы. Так как работа внешних сил W положительна, то работа внутренних сил V будет отрицательной: W=–V. Определим работу внутренних сил M, Q, N плоской стержневой системы.

а) Работа продольной силы N Пара продольных сил N , действующих на элемент dx , приводят к его чистому растяжению: По теореме Клапейрона, эти силы на общей деформации элемента N совершают действительную работу С учетом закона Гука при растяжении получим где E – модуль Юнга, F – площадь сечения, EF – жесткость на растяжение. =NN 1 d. V N. 2 N N dx = EF , 2 N Nd. V = dx 2 EF NN Ndx

б) Работа изгибающего момента M Пара изгибающих моментов M , действующих на элемент dx , приводят к его чистому изгибу : На общей деформации M эти моменты совершают работу По закону Гука Значит, где I – момент инерции сечения, E I – жесткость на изгиб. . M M dx = EI , 2 M Md. V = dx 2 EI M M 1 d. V = M · .

в) Работа поперечной силы Q Действие пары поперечных сил Q приводит к чистому сдвигу элемента dx : На общей деформации Q они совершают работу По закону Гука где – коэффициент формы сечения, GF – жесткость на сдвиг. Поэтому , Q Q dx = GF . 2 Q Q d. V = dx 2 GF QQ 1 d. V = Q · . 2 Q Q Q

Воспользуемся принципом суперпозиции: Если проинтегрировать это выражение по всей длине элемента l и учесть наличие в системе n стержней, получим: = 2 2 2 M Q N 1 Q NM d. V = (d. V + d. V ) μ dx. EF GF ΕΙ 2 2 2 2 1 M Q N U Vμ dx 2ΕΙ GF EF − потенциальная энергия стержневой системы

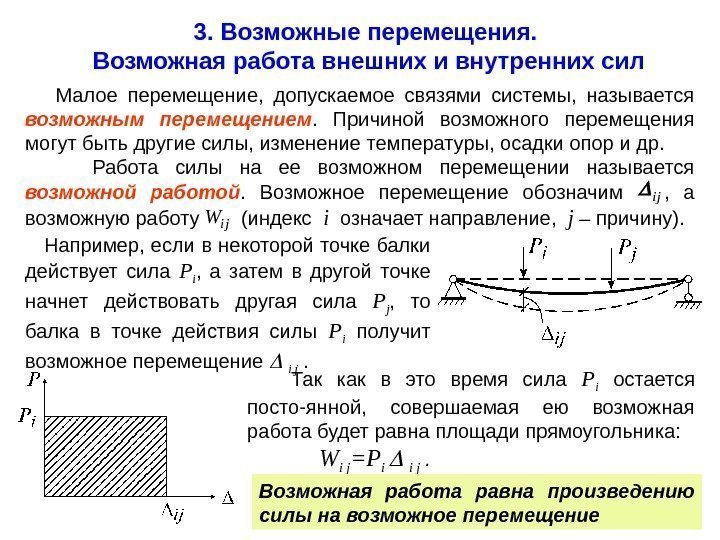
Малое перемещение, допускаемое связями системы, называется возможным перемещением. Причиной возможного перемещения могут быть другие силы, изменение температуры, осадки опор и др. Работа силы на ее возможном перемещении называется возможной работой. Возможное перемещение обозначим , а возможную работу (индекс i означает направление, j – причину). ij i j. W 3. Возможные перемещения. Возможная работа внешних и внутренних сил Например, если в некоторой точке балки действует сила P i , а затем в другой точке начнет действовать другая сила P j , то балка в точке действия силы P i получит возможное перемещение i j . Так как в это время сила P i остается посто-янной, совершаемая ею возможная работа будет равна площади прямоугольника: W i j =P i i j . Возможная работа равна произведению силы на возможное перемещение

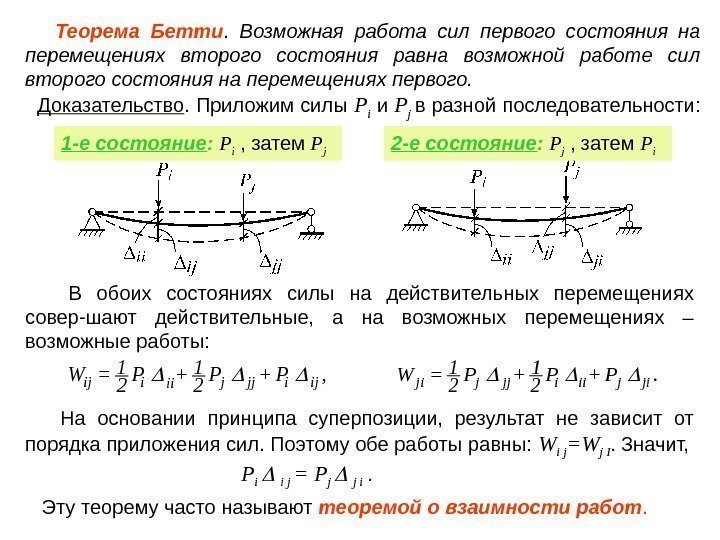
Теорема Бетти. Возможная работа сил первого состояния на перемещениях второго состояния равна возможной работе сил второго состояния на перемещениях первого. Доказательство. Приложим силы P i и P j в разной последовательности: В обоих состояниях силы на действительных перемещениях совер-шают действительные, а на возможных перемещениях – возможные работы: На основании принципа суперпозиции, результат не зависит от порядка приложения сил. Поэтому обе работы равны: W i j =W j I. Значит, P i i j = P j j i . Эту теорему часто называют теоремой о взаимности работ. , ij i j jj iijii 1 1 W = P + P 2 2 . j i j jijj ii 1 1 W = P + P 2 2 1 -е состояние : P i , затем P j 2 -е состояние : P j , затем P i

Определим возможную работу внутренних сил. Для этого рассмотрим два состояния системы: 1) действие силы P i − она вызывает внутренние усилия M i , Q i , N i ; 2) действие силы P j − пусть она вызывает возможные деформации Внутренние усилия первого состояния на деформациях второго состояния совершат возможную работу: Если это выражение проинтегрировать по длине элемента l и учесть наличие в системе n стержней, получим формулу: j Mj Mdx , EI j Q dx , GF j Nj N dx. EF . i j i j ij i M j i Q j i j. N M M Q Q N N d. V = M + Q + N = dx dx dx EI GF EF i j i j M M Q Q N N V μ dx EI GF EF − возможная работа внутренних сил

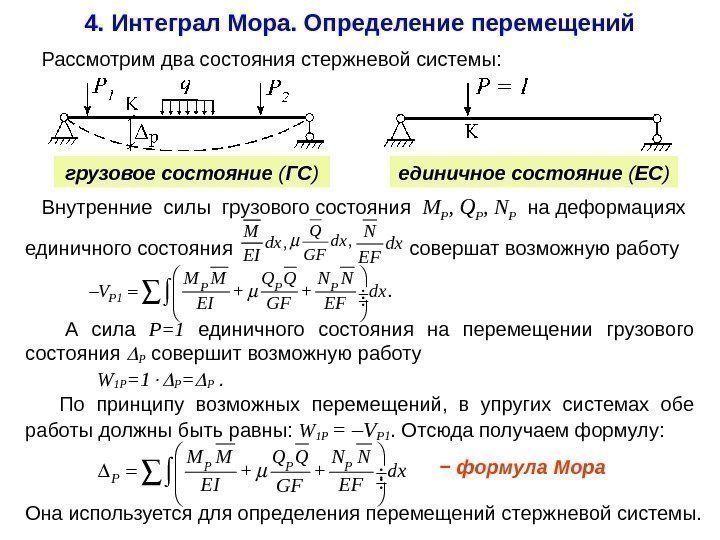
Внутренние силы грузового состояния M P , Q P , N P на деформациях единичного состояния совершат возможную работу 4. Интеграл Мора. Определение перемещений А сила P =1 единичного состояния на перемещении грузового состояния P совершит возможную работу W 1 P =1 P = P . По принципу возможных перемещений, в упругих системах обе работы должны быть равны: W 1 P = –VP 1. Отсюда получаем формулу: , Μ dx EI , Q dx GF N dx EF. P P 1 M M Q Q N N V + + dx EI EFGF P P M M Q Q N N + + dx EI EFGF Она используется для определения перемещений стержневой системы. − формула Мора Рассмотрим два состояния стержневой системы: грузовое состояние ( ГС ) единичное состояние ( ЕС )

Возможны три случая : 1) если 8 , учитываются лишь моменты: 2) если 5≤ ≤ 8 , учитываются и поперечные силы: 3) если 5 , формула Мора дает большую погрешность. В этом случае перемещения следует определять методами теории упругости. 5. Отдельные случаи применения формулы Мора h l. P P M M dx EI h l. P P P M M Q Q + dx EIGF 1) В балках

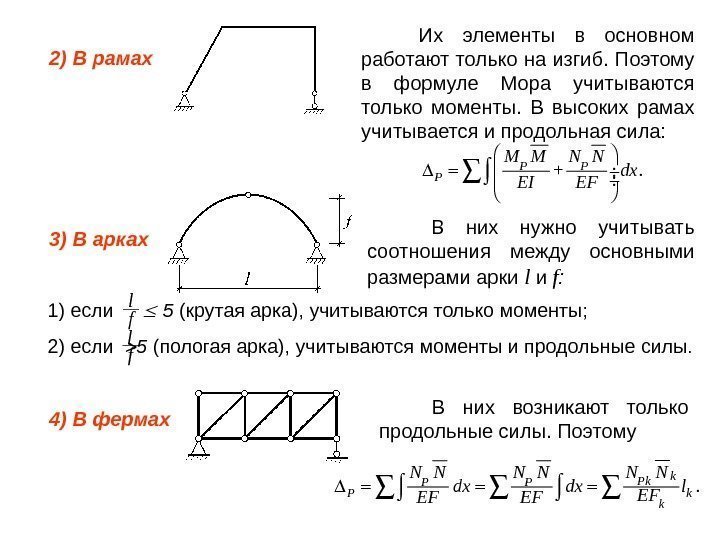
1) если 5 (крутая арка), учитываются только моменты; 2) если 5 (пологая арка), учитываются моменты и продольные силы. . P P P M M N N + dx EFEI fl fl. k. P P P k k N NN N dx dx l. EFEF EF 2) В рамах 3) В арках 4) В фермах Их элементы в основном работают только на изгиб. Поэтому в формуле Мора учитываются только моменты. В высоких рамах учитывается и продольная сила: В них нужно учитывать соотношения между основными размерами арки l и f : В них возникают только продольные силы. Поэтому