Лекція 4. Закон збереження імпульсу та моменту імпульсу

Лекція 4. Закон збереження імпульсу та моменту імпульсу • 1. Центр мас. • 2. Імпульс замкнутої системи • 3. Пружний і непружний удари • 4. Реактивний рух • 5. Закон збереження моменту імпульсу • 6. Задача двох тіл • 7. Рух в полі центральних сил

Центр мас • Імпульс системи частинок в інерціальній системі відліку К: • Перейдемо до іншої інерціальної системи К ’, яка рухається зі швидкістю , так щоб • Оскільки то • Звідси 0 i iimp 0 i iimp , u 0 i i ii mumump i ii ii m m u u

Центр мас • Точка, відносно якої повний імпульс дорівнює нулю, називається центром мас, або центром інерції. Тому u – швидкість центра мас uc. • Звідси координати центра мас. • Повний імпульс можна подати як добуток повної маси на швидкість центра мас. i ii ii c m rm r i iic mu. Mp

Імпульс замкнутої системи • У відсутності зовнішніх сил ( F = 0) p = const — повний імпульс зберігається. ik iiki FF dt pd i i ii FFp dt d dt pd

Пружний і непружний удари • Замкнена система. Абсолютно непружний удар (тіла злипаються). Маси m 1 і m 2. Швидкості до удару 10 і 20. Із закону збереження сумарного імпульсу • При цьому енергія не зберігається, оскільки відбулось розсіяння енергії на нагрівання тіл. 21202101 mmmm 21 202101 mm mm

Пружний і непружний удари • Розглянемо абсолютно пружний центральний удар. Із законів збереження енергії та імпульсу 22222 22 2 11 2 202 2 101 mmmm 2211202101 mmmm 2 20 2 22 2 101 mm 20221101 mm

Пружний і непружний удари 21 1021202 1 2 mm mmm 21 2012101 2 2 mm mmm Якщо m 1 = m 2 , тоді 1 = 20 і 2 = 10 , зокрема, якщо 10 = 0, тоді 2 = 0.

Пружний удар

Удар об стінку • Якщо кулька ударяється об стінку, можна ототожнити стінку з кулькою масою m → ∞. В такому разі • Якщо стінка стоїть ( 20 = 0), тоді кулька відбивається назад з тією ж швидкістю. • Коли стінка рухається назустріч кульці, швидкість кульки зростає на 2 20 і зменшується на 2 20 , якщо стінка тікає від кульки. 20210201 ,

Відбивання м’яча від стінки

Співударяння кульок. Нецентральний удар

Реактивний рух • Якщо тіло з масою m розірветься ( m = m 1 + m 2 ) , то осколки отримають швидкості 1 і 2. Оскільки зовнішніх сил немає, то повний імпульс залишиться незмінним. Якщо на початку р = 0, то і вкінці • Звідси • Надалі швидкості залишаються сталими. 0 2211 mmp 1 21 2 m m

Реактивний рух • При реактивному русі тіла його маса змінюється (1897 р. І. В. Мещерський). • Нехай в момент часу t швидкість ракети дорівнює , швидкість газів відносно ракети o , а відносно Землі o — . dmmdmddpmp pp , dt dp dt dm dt dp p пал 0 dt dm dt dm 00 mm m m 0 0 00 lnln

Реактивний рух • В реальних ракетах маса палива не перевищує 80% маси ракети. Швидкість витікання газів при згорянні найкра-щого пального о ≤ 4 · 103 м/с. • Тому • А перша космічна швидкість І ≈ 8 км/с. см mm /1044, 6 2, 0 ln

Реактивний рух Вирішення проблеми: 1) збільшити о (ядерне паливо, фотонна ракета, плазмові прискорювачі), 2) зробити ракету багатоступінчатою (бак відділяється, маса зменшується і починається все спочатку).

Закон збереження моменту імпульсу • Розглянемо систему взаємодіючих частинок, на які діють зовнішні сили 11211 FFm 22122 FFm 11121111 Fr. Frrm 22212222 Fr. Frrm

Закон збереження моменту імпульсу • Оскільки rrrrr dt d 1112111111 Fr. Frpr dt d m 2221222222 Fr. Frpr dt d m 221112212211, Fr. Frrprpr dt d ( = 0 )

Закон збереження моменту імпульсу. MFr dt Ld pr dt d i ii Якщо момент зовнішніх сил М = 0, тоді const. L dt Ld 0 Якщо діє пара сил, , тоді 21 FF 1121212211 Fr. Fr. Fr. M — момент імпульсу замкнутої системи незмінний

Рух в полі центральних сил. Задача двох тіл. 21 2211 mm rmrm r C В системі центра мас r c = 0, 2211 rmrm Введемо 12 rrr r mm m r 21 1 2 21 2 1,

Рух в полі центральних сил. Задача двох тіл. r erf. FF 2112 rr erfrm 2211 , rerf mmrrr 2112 11 21 21 21 111 mm mm mm — приведена маса

Рух в полі центральних сил rerf. F рухуплощиніLMconstpr. L , 0, Площина орбіти фіксована, r завжди в одній площині. dt m. L dtpr mdtrd. S 22 1 21 Площа сектора d. S r d p const m L dt d. S

Еліптичні орбіти планет. Закони Кеплера Перший закон Кеплера: планети рухаються по еліптичній орбіті, в фокусі якої знаходиться Сонце.

Закони Кеплера • Другий закон Кеплера: при русі планет по орбіті секторна швидкість залишається постійною. const m L dt d. S 2 zremrermrrmrmrm. L 2 Оскільки тоerer rr ,

Закони Кеплера • Третій закон Кеплера або

Космічні траєкторії Для гравітаційних сил r U r rf , 2 2222 rr const r mrrm r m E 2222 const. Lmr. L z 2 З цієї системи рівнянь можна знайти r ( t ) і ( t ) , тобто розрахувати траєкторію руху планети.

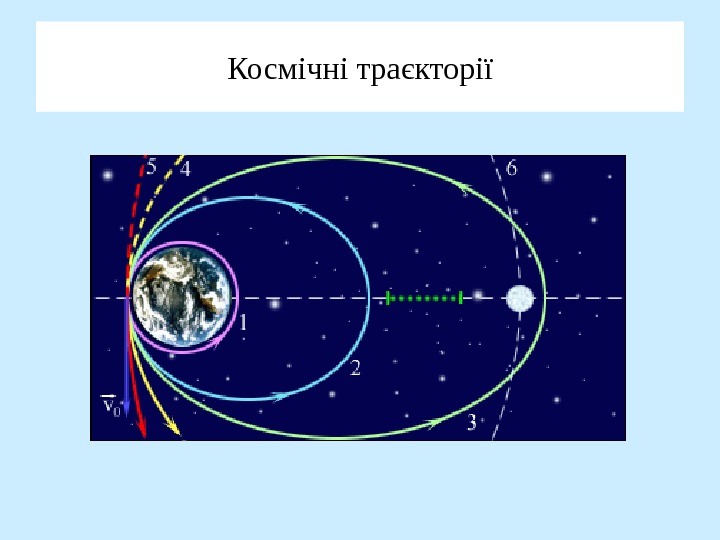
Космічні траєкторії

Орбіти еліптична геостаціонарна

Космічні траєкторії • Виявилось, що у випадку, коли повна енергія E < 0, траєкторією є еліпс. Коли Е = 0, отримаємо параболу. • В цих випадках 0, отримаємо гіперболу. При цьому величина може бути як більшою, так і меншою нуля. • Коли ми розглядаємо гравітаційне поле, завжди < 0. Поле електричних зарядів може відповідати як 0 — відштовхування однойменних зарядів. В останньому випадку траєкторія може бути лише гіперболічною.

Енергія тіла в гравітаційному полі планети

Космічні швидкості