ЛЕКЦИЯ 4 ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ 4 1 Волновая

ЛЕКЦИЯ 4. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ 4. 1 Волновая функция микрочастицы и ее свойства

Вероятностное описание состояний микрообъектов С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большое число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после дифракции, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности.

Волны де Бройля – волны вероятности? Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля: Можно ли волны де Бройля истолковывать как волны вероятности, то есть считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

Амплитуда вероятности Чтобы устранить эти трудности, немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а амплитуда вероятности (х, у, z, t). Эту величину называют также волновой функцией (или псифункцией). Амплитуда вероятности может быть комплексной, и вероятность P пропорциональна квадрату её модуля: Т. о. , описание состояния микрообъекта с помощью волновой функции имеет статистический, характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами х и x + dx, у и y + dy, z и z + dz.

Волновая функция Волновой функция – основной носитель информации об корпускулярных и волновых свойствах микрочастиц. Вероятность d. P нахождения частицы в элементе объемом d. V равна Где | |2 = d. P/d. V – плотность вероятности, определяющая вероятность нахождения микрочастицы в единичном объеме в окрестности точки с координатами x, y, z. Вероятность P найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна

Условие нормировки Так как | |2 d. V определяется как вероятность, то необходимо волновую функцию нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объём V принять бесконечный объём всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей Таким образом, это условие говорит об объективном существовании частицы в пространстве.

Условия, накладываемые на волновую функцию Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий. Функция , характеризующая вероятность обнаружения микрочастицы в элементе объема, должна быть конечной (поскольку вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

Принцип суперпозиции Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями 1, 2, . . . , i, . . . то она также может находиться в состоянии , описываемом линейной комбинацией этих функций: Здесь Ci – вообще говоря, комплексные числа, квадрат каждого из которых пропорционален вероятности пребывания микрочастицы в состоянии с номером i.

Парадокс «кот Шредингера» В закрытый ящик одновременно помещен воображаемый кот, а также такой же воображаемый механизм с радиоактивным ядром и емкостью с ядовитым газом. Согласно эксперименту, если ядро распадется, то оно приведет механизм в действие: емкость с газом откроется и кот умрет. Вероятность распада ядра составляет 1 к 2. Парадокс заключается в том, что согласно квантовой механике если над ядром не производят наблюдение, то кот находится в так называемой суперпозиции, другими словами кот одновременно находится во взаимоисключающих состояниях (он одновременно жив и мертв). Однако если наблюдающий откроет ящик, он может убедиться, что кот находится в одном конкретном состоянии: он или жив, или мертв. По мнению Шредингера, неполнота квантовой теории состоит в том, что она не уточняет, при каких условиях кот перестает быть в суперпозиции и оказывается либо живым, либо мертвым.

Парадокс «кот Шредингера»

Принцип суперпозиции Сложение волновых функций (амплитуд вероятностей), а не самих вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

ЛЕКЦИЯ 4. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ 4. 2 Уравнение Шредингера

Описание состояния микрочастицы в квантовой механике Пусть частица массы m движется в силовом поле с потенциальной энергией (x, y, z, t). В этом случае волновую функцию , описывающую такое движение микрочастицы в квантовой механике, следует находить из решения дифференциального уравнения, которое называется общим уравнением Шредингера

Движение микрочастицы в стационарном силовом поле Если силовое поле, в котором движется микрочастица, является стационарным (потенциальная энергия частицы в токам поле не зависит от времени), и в такой стационарной задаче полная энергия частицы E не изменяется со временем, то волновую функцию микрочастицы можно представить в виде произведения пространственной и временной частей:

Волновая функция микрочастицы в стационарном силовом поле Подставляя это выражение во временное уравнение Шредингера и разделяя в нем переменные, можно найти вид волновой функции микрочастицы в стационарном силовом поле: Тогда

Уравнение Шредингера для стационарных состояний Координатная часть волновой функции (x, y, z) называется волновой фукнцией стационарной задачи. Эта функция является решением уравнения Шредингера для стационарных состояний:

Замечание С помощью волновой функции, найденной из решения уравнения Шредингера, можно описывать квантовые состояния только нерелятивистских частиц, которые движутся со скоростями, много меньшими скорости света в вакууме c = 3 108 м/с.

ЛЕКЦИЯ 4. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ 4. 3 Представление физических величин операторами

Понятие оператора Для получения из волновой функции информации о физических величинах, связанных с движением частицы, в квантовой механике каждой физической величине ставится в соответствие линейный оператор этой физической величины, действие которого на волновую функцию преобразует ее в другую функцию по определенному правилу. Оператор физической величины изображается в виде буквенного символа этой величины со «шляпкой» в виде значка « » на буквой:

Соотношения между операторами в квантовой механике имеют ту же структуру, что и соотношения между соответствующими физическими величинами в классической механике

Оператор координаты Его действие на волновую функцию сводится к умножению ее на соответствующую координату: или в символической операторной форме: Тогда оператор радиуса-вектора частицы:

Оператор импульса Операторы проекций импульса определяются как а операторы вектора импульса и квадрата импульса записываются в виде:

Оператор момента импульса Оператор проекций момента импульса определятся как Оператор квадрата момента импульса:

Оператор кинетической и потенциальной энергий частицы Из классической связи кинетической энергии частицы с квадратом ее импульса получаем связь между соответствующими операторами. Поэтому оператор кинетической энергии Если частица движется в силовом поле и ее потенциальная энергия зависит только от координат: = (x, y, z) и определена в любой точке пространства, то оператор потенциальной энергии определяется как оператор умножения на функцию :

Гамильтониан Оператор поной энергии (или гамильтониан) определяется как сумма операторов кинетической и потенциальной энергий: Основное уравнение квантовой механики – общее (временное) уравнение Шредингера может быть записано в т. н. «операторной форме» , содержащей гамильтониан: а уравнение Шредингера для стационарных состояний представимо в виде

Среднее значение физической величины Среднее значение (математическое ожидание) результатов измерений физической величины A, не имеющей определенного значения, можно найти по формуле Можно показать, что в стационарных квантовых состояниях среднее значение физической величины, оператор которой не зависит явно от времени, остается постоянным.

ЛЕКЦИЯ 4. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ 4. 4 Микрочастица в бесконечно глубокой прямоугольной потенциальной яме

Стационарные состояния в квантовой механике В квантовой механике существует класс задач движения микрочастиц в силовых полях, для которых потенциальная энергия не зависит явно от времени: Такие силовые поля называются стационарными силовыми полями. В стационарных состояниях квантовая система может находиться в состояниях с определенным значением энергии E. Эти состояния называются стационарными состояниями, а задачи о движении частиц, находящихся в таких состояниях, стационарными задачами квантовой механики.

Волновая функция частицы в стационарном состоянии Волновая функция частицы, находящейся в стационарном квантовом состоянии, имеет вид где – это координатная часть волновой функции, которую в стационарных задачах часто называют просто волновой функцией стационарного состояния. Она удовлетворяет уравнению Шредингера для стационарных состояний

Постановка задачи о движении частицы в потенциальной яме с непроницаемыми стенками Рассмотрим движение частицы в потенциальной яме с непроницаемыми стенками, т. е. бесконечно высокими стенками. Такие ямы называют потенциальными ящиками, наиболее часто это название применяется по отношению к трехмерной потенциальной яме. В этом случае частица находится в ограниченной области пространства, т. е. мы имеем дело с так называемым финитным движением

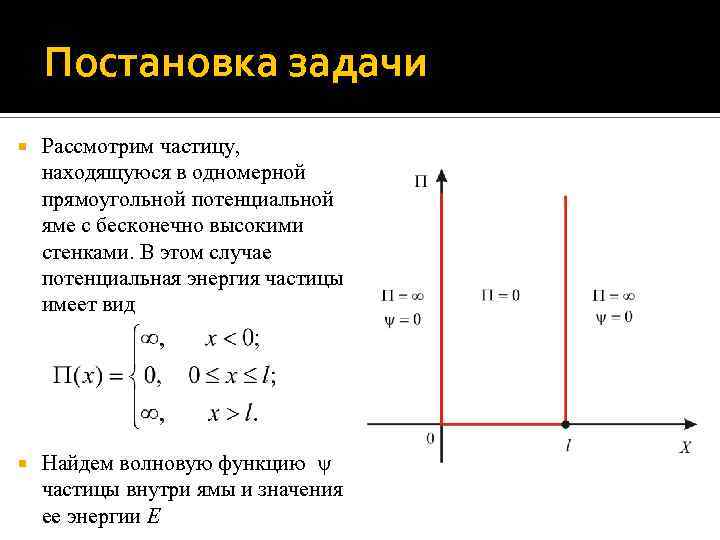Постановка задачи Рассмотрим частицу, находящуюся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. В этом случае потенциальная энергия частицы имеет вид Найдем волновую функцию частицы внутри ямы и значения ее энергии E

Общее решение уравнения Шредингера для частицы в одномерной потенциальной яме Вне потенциальной ямы частица находиться не может, следовательно Запишем стационарное уравнение Шредингера для частицы внутри потенциальной ямы ( = 0): Общее решение этого уравнения:

Граничные условия Константы k и 0 найдем из граничных условий, накладываемых на волновую функцию:

Энергетический спектр частицы в одномерной потенциальной яме Находим возможные значения энергий частицы в одномерной потенциальной яме: Важной особенностью полученного энергетического спектра является его дискретность: частица, находящаяся в бесконечно глубокой потенциальной яме, может иметь только дискретные, определяемые квантовым числом n значения энергии.

Энергетический спектр частицы в одномерной потенциальной яме Разность энергий соседних энергетических уровней равна и увеличивается с ростом числа n. Рассмотрим соотношение т. е. с увеличением числа n дискретность энергетического спектра играет все меньшую роль. Данный результат – проявление важного физического принципа – принципа соответствия, согласно которому при больших значениях квантового числа n квантовая механика переходит в механику классическую

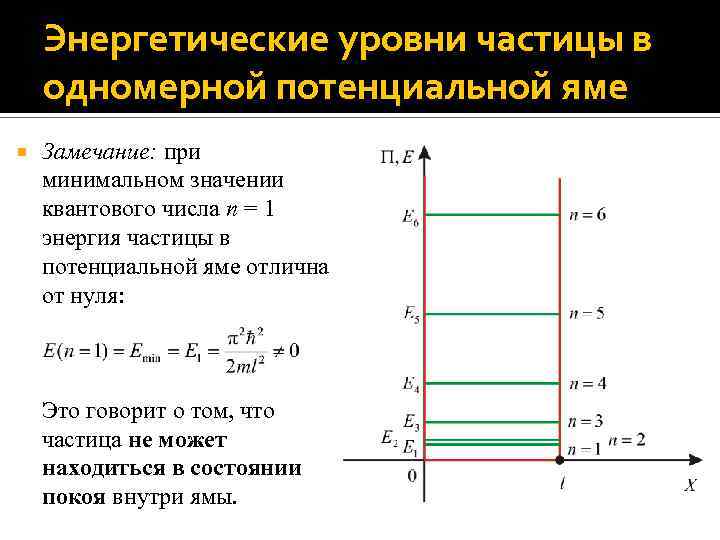Энергетические уровни частицы в одномерной потенциальной яме Замечание: при минимальном значении квантового числа n = 1 энергия частицы в потенциальной яме отлична от нуля: Это говорит о том, что частица не может находиться в состоянии покоя внутри ямы.

Волновая функция частицы Найдем постоянную A из условия нормировки волновой функции: Тогда окончательно волновая функция частицы будет иметь вид

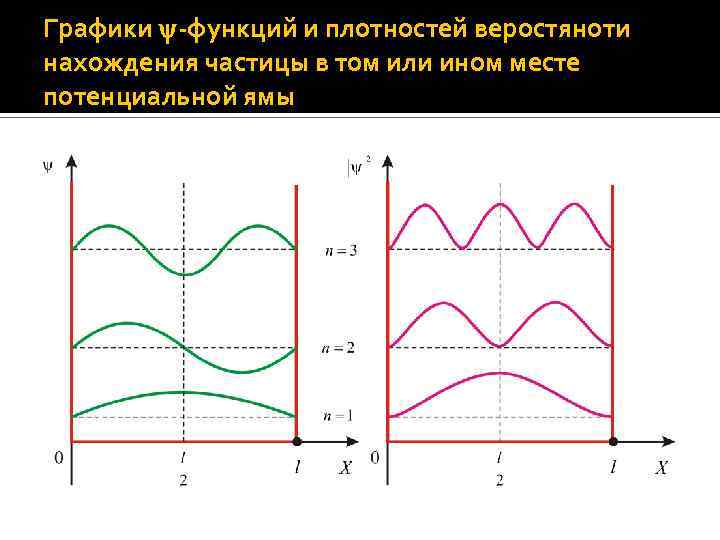Графики -функций и плотностей веростяноти нахождения частицы в том или ином месте потенциальной ямы

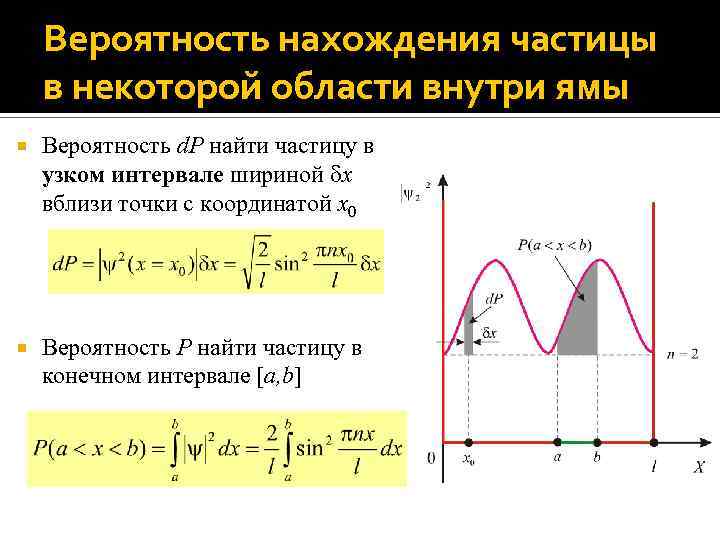Вероятность нахождения частицы в некоторой области внутри ямы Вероятность d. P найти частицу в узком интервале шириной x вблизи точки с координатой x 0 Вероятность P найти частицу в конечном интервале [a, b]

Трехмерная потенциальная яма Рассмотрим частицу, находящуюся в трехмерной потенциальной яме с бесконечно высокими стенками (потенциальный ящик). Обозначим через внутреннюю область прямоугольного параллелепипеда. В данной задаче потенциальная энергия частицы имеет вид:

Волновая функция частицы Вне потенциального ящика волновая функция частицы равна нулю: = 0. Внутри ямы

Энергетический спектр частицы Таким образом, квантовое состояние частицы и ее энергия в трехмерной потенциальной яме определяются заданием трех квантовых чисел n 1, n 2, n 3. Энергетический спектр частицы, как и в случае одномерной ямы, является дискретным.

Частный случай: кубическая яма В случае кубической потенциальной ямы (l 1 = l 2 = l 3 = l) волновая функция частицы и ее энергетический спектр имеют вид

Вырожденные уровни Из приведенных формул следует, что если n 1 n 2 n 3, то одному и тому же энергетическому уровню (значению энергии), определяемому этими квантовыми числами, соответствует 6 различных состояний частицы, описываемых волновыми функциями. Энергетический уровень, которому соответствует не одно, а несколько состояний частицы, называется вырожденным уровнем, а число соответствующих ему состояний называется кратностью вырождения уровня. Энергетические уровни в кубической яме, для которых n 1 n 2 n 3, являются невырожденными, все остальные уровни вырождены. Если два квантовых числа равны между собой и не равны третьему числу, то кратность вырождения соответствующего уровня равна 3. Если же все три квантовых числа разные – кратность вырождения равна 6.

ЛЕКЦИЯ 4. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ 4. 5 Туннельный эффект

Постановка задачи Потенциальным барьером называется область пространства, в которой потенциальная энергия частицы больше, чем в окружающих областях. Рассмотрим движение частицы в области одномерного прямоугольного потенциального барьера, для которого потенциальная энергия частицы имеет вид

Высокий потенциальный порог: вид стационарного уравнения Шредингера Запишем стационарные уравнения Шредингера для областей I, II и III движения частицы: Стационарное уравнение Шредингера Область III

Высокий потенциальный порог: общее решение стационарного уравнения Шредингера Общие решения стационарного уравнения Шредингера для областей I, II и III соответственно имеют вид: В выражении для 1 первое слагаемое описывает падающую на порог волну де Бройля частицы, второе слагаемое – отраженную волну. В выражении для 2 учтено, что волновая функция не может неограниченно возрастать при x . В выражении для 1 учтено, что оно описывает только волну де Бройля частицы, движущейся в положительном направлении оси X. Положим также A = 0. Тогда

Потенциальный барьер: граничные условия С помощью граничных условий можно найти коэффициент прохождения потенциального барьера:

Коэффициента прохождения потенциального барьера В случае, если ширина барьера a удовлетворяет условию то коэффициент прохождения частицы через барьер (или коэффициент прозрачности барьера) есть Коэффициент прохождения потенциального барьера испытывает сильную (экспоненциальную зависимость) от ширины a барьера, массы m частицы и разности энергий 0 – E.

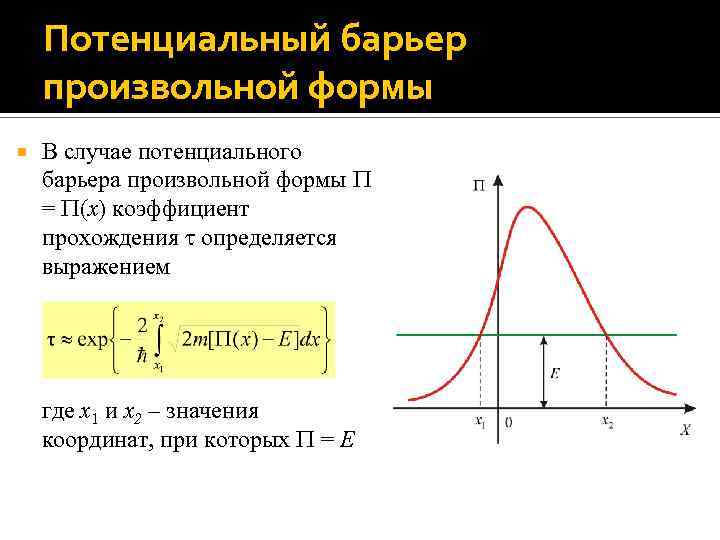Потенциальный барьер произвольной формы В случае потенциального барьера произвольной формы = (x) коэффициент прохождения определяется выражением где x 1 и x 2 – значения координат, при которых = E

Туннельный эффект Прохождение частицы через потенциальный барьер, высота которого превышает энергию частицы, получило название туннельного эффекта. При этом полная энергия частицы остается неизменной. Отметим, что туннельный эффект представляется собой чисто квантовое явление. Классическая частица, подходя к барьеру, высота которого больше ее полной энергии, всегда отражается от него; пройти такой барьер она не может. Туннельный эффект объясняет ряд важных физических явлений, таких, как, например, холодная эмиссия электронов из металла, радиоактивный распад ядер, контактную разность потенциалов и др. Кроме того, туннельный эффект находит широкое применение в технических приложениях. В частности, на его основе создан сканирующий туннельный микроскоп (СТМ), являющийся основой исследования физики и технике поверхности и имеющий широкие перспективы в связи с развитием нанотехнологий.

Надбарьерное прохождение При движении микрочастицы над прямоугольным потенциальным барьером коэффициент прохождения имеет вид В общем случае из-за наличия надбарьерного прохождения коэффициент прохождения < 1. Этот коэффициент обращается в единицу только при значениях энергии частицы, определяемых соотношением

ЛЕКЦИЯ 4. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ 4. 6 Квантовый гармонический осциллятор

Гармонический осциллятор Гармоническим осциллятором называется система, способная, при ее описании в рамках классической механики, совершать гармонические колебания. В физике модель гармонического осциллятора играет важную роль, особенно при исследованиях малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т. д.

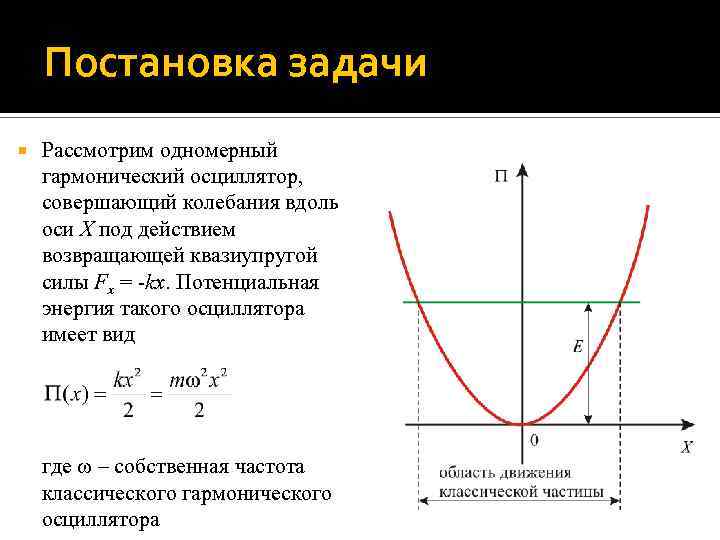Постановка задачи Рассмотрим одномерный гармонический осциллятор, совершающий колебания вдоль оси X под действием возвращающей квазиупругой силы Fx = -kx. Потенциальная энергия такого осциллятора имеет вид где – собственная частота классического гармонического осциллятора

Стационарное уравнение Шредингера для квантового гармонического осциллятора. В квантовой механике для анализа задачи о гармоническом осцилляторе нужно решить стационарное уравнение Шредингера с данной потенциальной энергией:

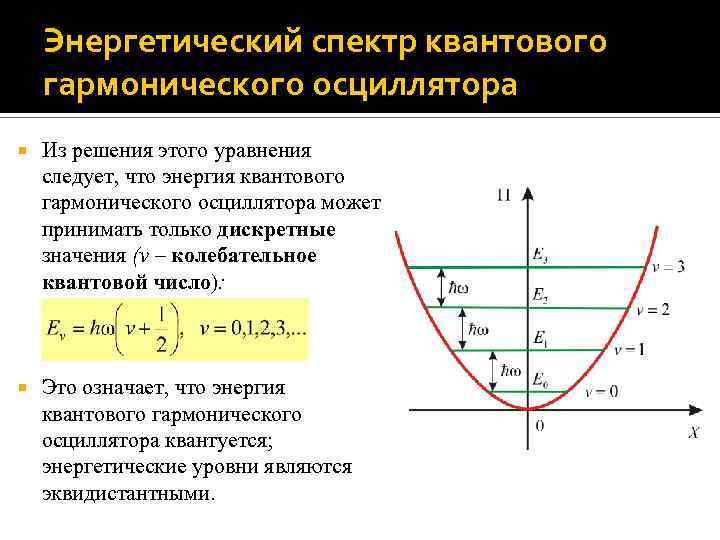Энергетический спектр квантового гармонического осциллятора Из решения этого уравнения следует, что энергия квантового гармонического осциллятора может принимать только дискретные значения (v – колебательное квантовой число): Это означает, что энергия квантового гармонического осциллятора квантуется; энергетические уровни являются эквидистантными.

Волновые функции квантового гармонического осциллятора Значение колебательного квантового числа v=0 v=1 v=2 Волновая функция соответствующего состояния

Волновые функции квантового гармонического осциллятора Отрезок [-a 0, a 0] определяет область значений координаты x, в которой совершал бы колебания классический осциллятор

Нулевые колебания При v = 0 квантовый гармонический осциллятор обладает минимальной энергий Это означает, что даже при нулевой температуре квантовый гармонический осциллятор обладает ненулевой энергией колебаний. Классическое же решение задачи допускает решения, соответствующие покоящемуся осциллятору с энергией, равной нулю.

Правило отбора. Излучение фотона При переходе с одного уровня энергии на другой должно выполняться правило отбора: v = 1, т. е. переходы возможны лишь между соседними энергетическими уровнями. При переходе с верхнего уровня на нижний испускается квант электромагнитного излучения с энергией, равной разности энергий этих уровней: Таким образом, величина в случае квантового гармонического осциллятора приобретает иной физический смысл: – это частота электромагнитного излучения, испущенного в результате перехода квантового гармонического осциллятора с состояние с меньшей энергией.