Лекция 3 Распределения, наиболее часто используемые в теории

Лекция 3 Распределения, наиболее часто используемые в теории надежности

1. Вейбулла t etp 0 0 — параметр формы, — параметр масштаба, t et. F 1 Функция распределения:

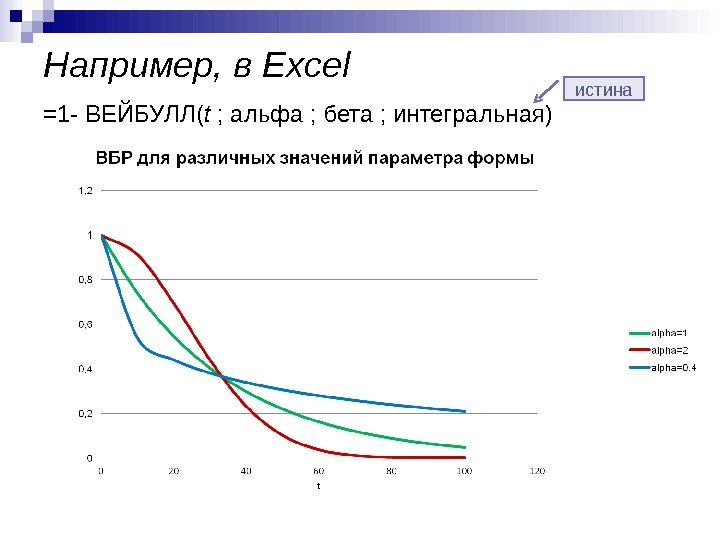
Например, в Excel = 1 — ВЕЙБУЛЛ( t ; альфа ; бета ; интегральная) истина

Моменты)/11()/21(* )/11(* 2 m В Excel Г( x ) = EXP ( ГАММАНЛОГ( x ))где Г( x ) – гамма-функция

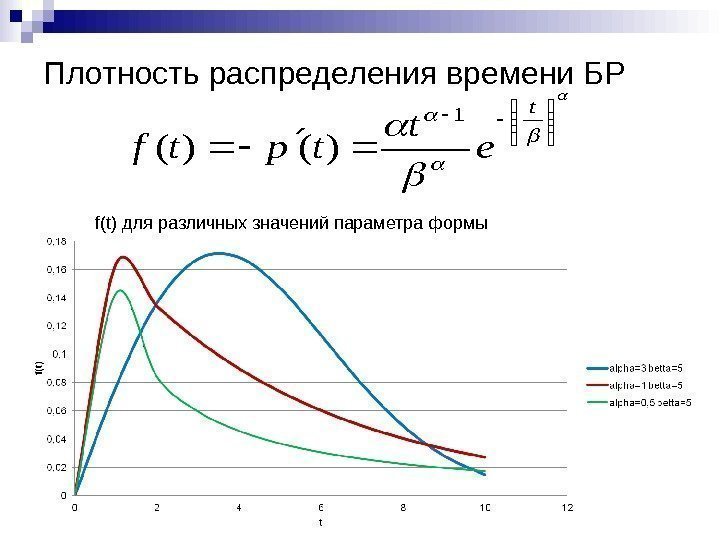
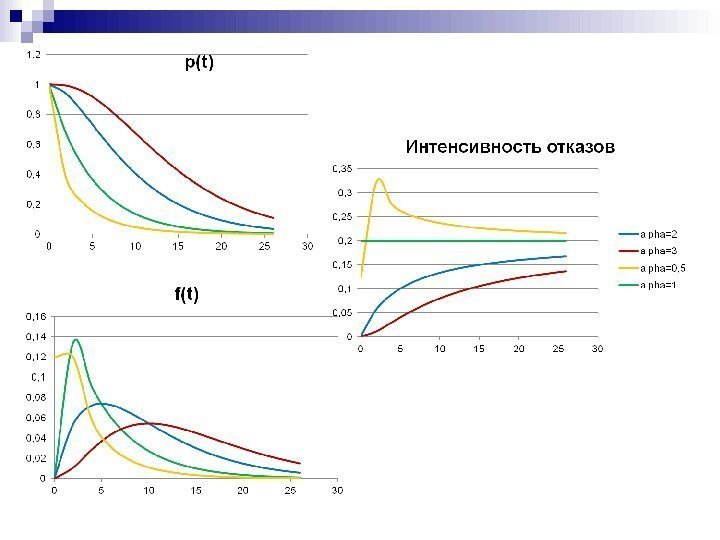
Плотность распределения времени БР t e t tptf 1 )()( f(t) для различных значений параметра формы

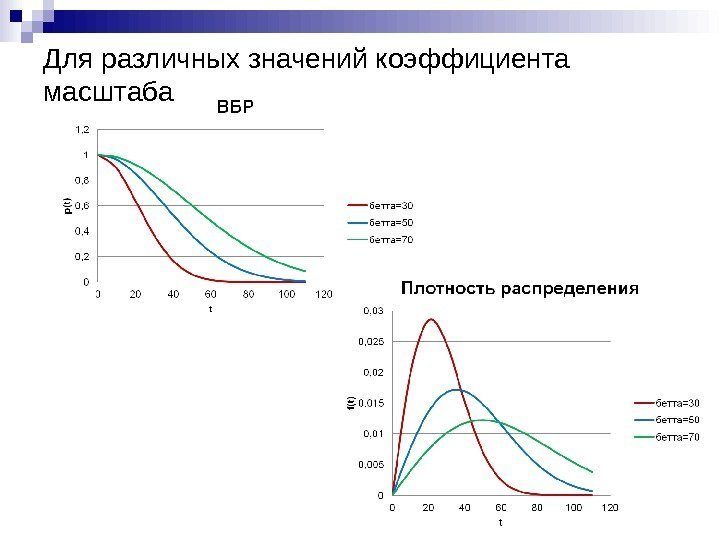
Для различных значений коэффициента масштаба

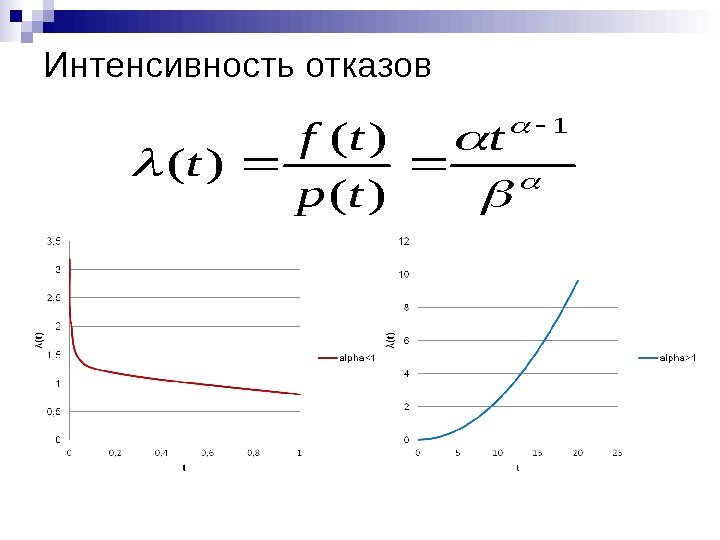
Интенсивность отказов 1 )( )( )( t tp tf t

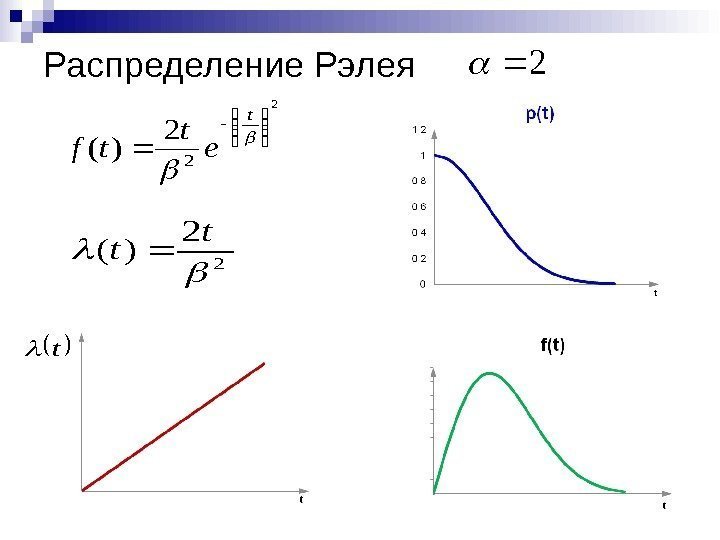
Распределение Рэлея 2 2 )( t e t tf 2 2 )( t t t

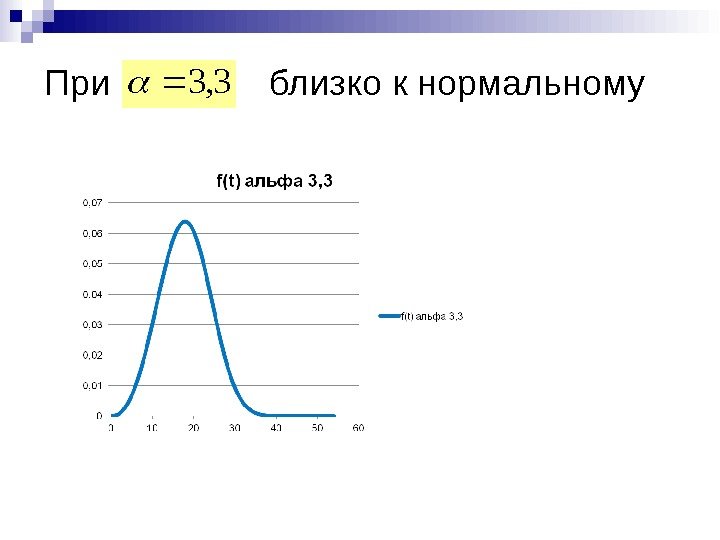
При близко к нормальному3,

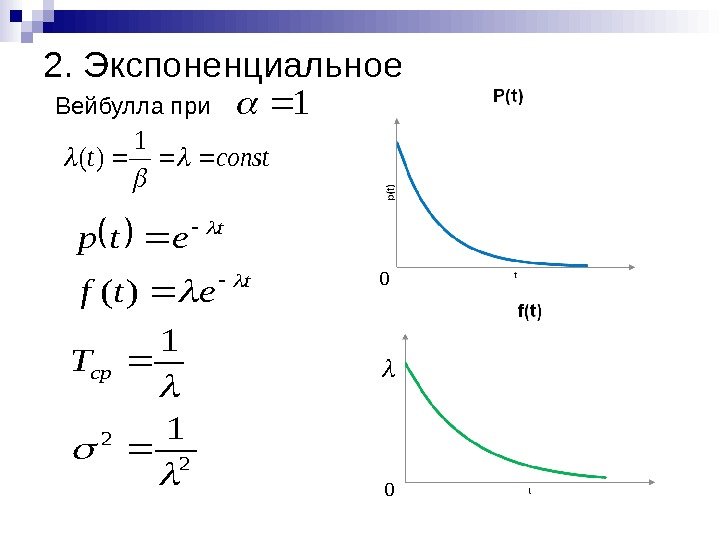
2. Экспоненциальное 1 2 21 1 )( ср t t T etf etp constt 1 )( Вейбулла при

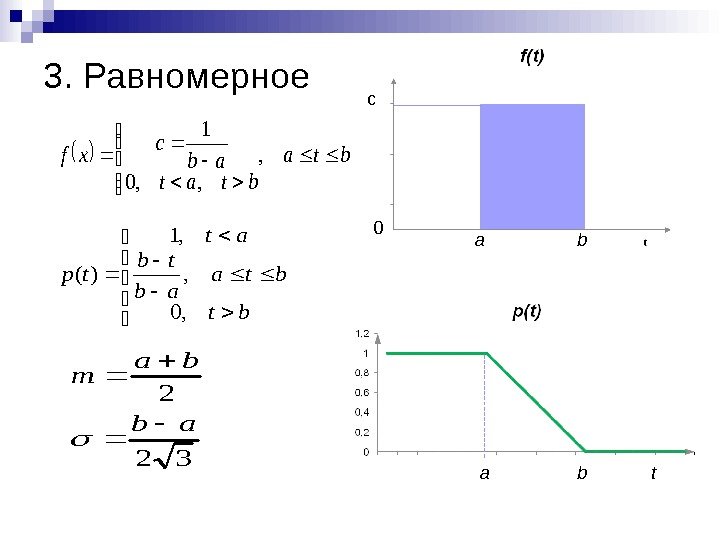
3. Равномерноеbta btat ab c xf , , , 0 1 bt bta ab tb at tp , 0 , , 1 )( 32 2 ab ba m tbc 0 a ba

4. Пуассоновский поток отказов Если интервалы между отказами имеют экспоненциальное распределение с параметром (и в предположении, что восстановление происходит мгновенно), то распределение вероятностей числа отказов на интервале (0, t ) подчиняется закону Пуассона с параметром . t

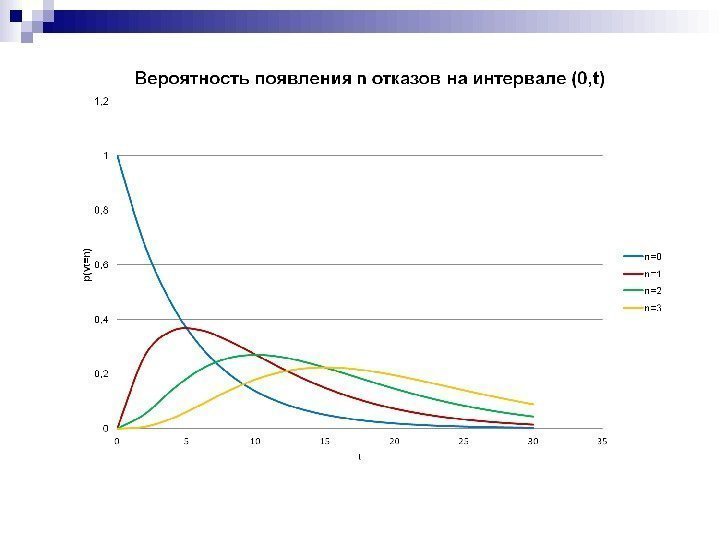
• Вероятность появления n отказов на (0, t ) : t n te n t n. P ! )( }{ • Среднее число отказов на (0, t ): tt. H)( • Интенсивность потока отказов: dt td. H t)( Любая конечная сумма независимых пуассоновских потоков отказов с параметрами m, , 1 является также пуассоновским потоком отказов с параметром m k k

Свойства Пуассоновского потока отказов: стационарность – вероятность возникновения фиксированного числа отказов на заданном интервале времени зависит только от длины интервала и не зависит от того, где на оси времени он расположен; ординарность – вероятность возникновения более чем одного отказа на малом интервале есть величина более высокого порядка малости, чем отсутствие последействия – вероятность возникновения фиксированного числа отказов на интервале не зависит от того, сколько отказов возникло до момента t. Поток отказов — простейший t t tt

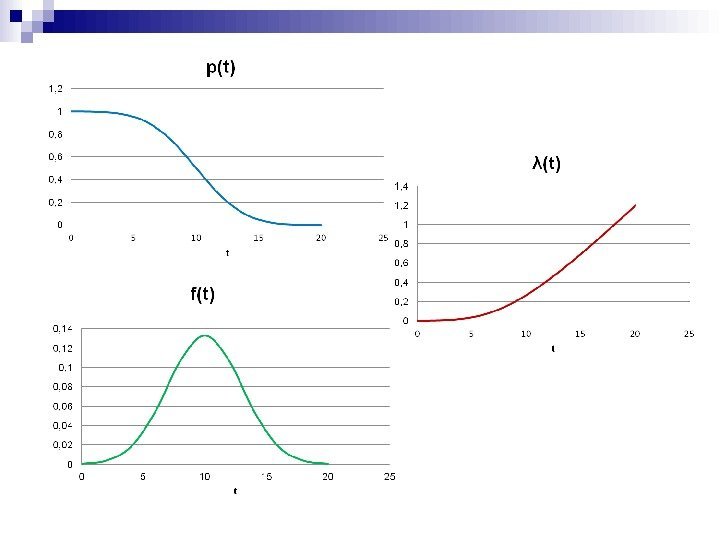
5. Нормальное распределение для моделирования процессов «старения» ] 2 )( exp[ 2 1 )(2 2 mt tf mt dxetp mx t 0 25, 0 2 12 2 где иm — параметры нормального распределения: математическое ожидание и среднеквадратичное отклонение времени безотказной работы элемента; dxet tx 0 2 2 1 — функция Лапласа

Свойства нормального распределения Сумма независимых случайных величин, имеющих нормальное распределение, также распределена по нормальному закону (математическое ожидание суммы равно сумме математических ожиданий, дисперсия суммы равна сумме дисперсий). Недостаток: не является односторонним (несущественно, если )cр. T

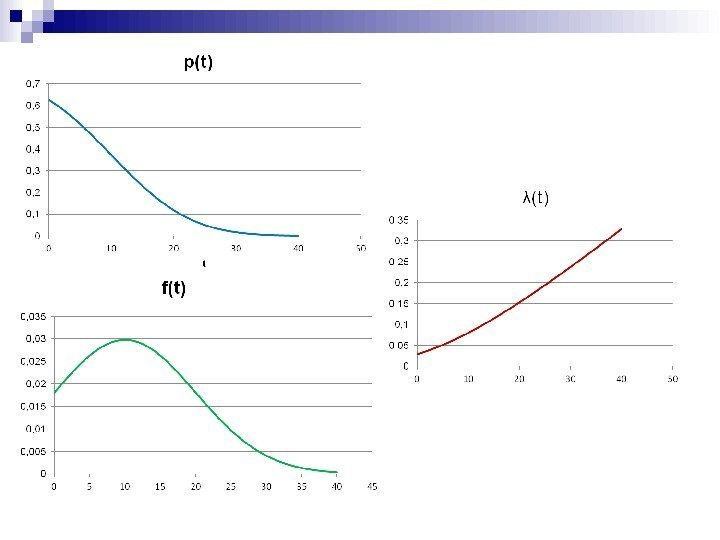
Усеченное нормальное распределение] 2 )( exp[ 2 )(2 0 0 mtc tf 00 иm — параметры усеченного нормального распределения; с — коэффициент определяемый из условия: 1 0 dttf 0 0 0 2 0 5, 0 2 2 0 mt cdxe c tp mx t

1 0 0 05, 0 m c. Математическое ожидание: 00 kmm , 1 2 0 0 0 k m k среднеквадратичное отклонение: 2 0 2 2 m e c k где

6. Гамма-распределение , 1 t e t tf параметры: и dxex x 0 1 — гамма-функция Математическое ожидание и среднеквадратичное отклонение: m Вероятность безотказной работы: dxe x tp x t

Свойства гамма-распределения Параметр определяет вид характеристик надежности при целом гамма-распределение называется распределением Эрланга порядка Сумма случайных величин, имеющих экспоненциальное распределение с параметром , имеет распределение Эрланга с параметрами: и

Распределение Эрланга 1 0! i i it i t etp cp. T 1 0 1 ! i i t t t

Использование Excel ВЕЙБУЛЛ, НОРМРАСП, ЭКСПРАСП, ГАММАРАСП и др. Функция Лапласа =НОРМРАСП(время; 0; 1; истина)-0, 5 Гамма функция = EXP( ГАММАНЛОГ( α ))dxet tx 0 2 2 1 dxexx