Лекция 3 Формализованное представление ЭА при автоматизированном

Лекция 3 Формализованное представление ЭА при автоматизированном проектировании 1 Описание графов с помощью матриц 2 Формальное описание коммутационных схем 3 Основная модель монтажного пространства

Вопрос 1 Описание графов с помощью матриц

Описание графов с помощью матриц 1. Матрица смежности Если задан граф G(X, U), то ему можно поставить в соответствие квадратную матрицу ( матрицу смежности ) размерностью n x n , где n – мощность множества вершин графа ( m – кратность смежных ребер ): nn ij a. A нет — если , 0 смежные_ , если , , ijji ij xxxxm a

Описание графов с помощью матриц 1. Матрица смежности. Пример X 1 X 2 X 3 X 4 01204 10133 21012 03101 4321 x x xxxx

Описание графов с помощью матриц 2. Матрица весовых соотношений строятся аналогично матрицам смежности, но значения их элементов определяются весом ребра графа ( Tij – вес связи ): nn ij c. C нет — если , 0 смежные_ , если , ijij ij xx. T c

Описание графов с помощью матриц 3. Матрица длин Это квадратная матрица ( Lij – длина ребра): nnijd. D нет — если , 0 смежные , если , ijij ij xx. L d

Описание графов с помощью матриц 4. Матрица инцидентности Представляет собой прямоугольную матрицу. Строки матрицы соответствуют вершинам, а столбцы – ребрам графаrn ij b. B нет — если , 0 смежные , если , 1 ij ij ux b

Описание графов с помощью матриц 4. Матрица инцидентности. Пример X 1 X 3 X 2 U 1 U 2 U 3 U 4 11003 01112 10111 4321 x x x uuuu

Описание графов с помощью матриц 5. Матрица смежности ребер Эта матрица, элементы которой образуются по правилуnn ij w. W нет — если , 0 смежные , если , 1 ij ij uu w

Описание графов с помощью матриц 5. Матрица смежности ребер. Пример X 1 X 3 X 2 U 1 U 2 U 3 U 4 01114 10113 11012 11101 4321 u u uuuu W

Вопрос 2 Формальное описание коммутационных схем

Формальное описание коммутационных схем Любую схему можно представить как некоторое подмножество элементов X L : n xxx. X 21 , соединенных между собой цепями из множества Е : m eee. E 21 , Представляя гиперграф H (X, E) матрицей инцидентности B получаем удобную форму представления схемы в памяти компьютера.

Формальное описание коммутационных схем Электрическую схему задают также в виде матрицы цепей : mn ij t. T Каждый элемент схемы имеет некоторое множество соединительных выводов, которые называются множеством контактов C. s ccc. C, ,

Формальное описание коммутационных схем Тогда любую схему можно задать в виде графа: WFCEXG, F – определяет принадлежность контактов из множества С элементам Х ; W — задаются вхождением контакта из множества С в цепи Е. si cxf, js ecw,

Формальное описание коммутационных схем (2 способ) Граф вида G задается обычно в виде трехмерной матрицы А, которую можно представить в виде двух матриц А 1, А 2. CE ij a. A 1 1 нет — если , 0 если , 11 js ij ec a CX ij a. A 2 2 нет — если , 0 если , 1 s 2 i ij xc a

Формальное описание коммутационных схем (Пример) VT 1 VT 2 1 2 3 4 X 1 R 2 R

Формальное описание схем (Пример) X 1 (VT 1) X 3 (R 1) X 2 (VT 2) X 4 (R 2) X 02 X 03 X 04 X 01 l 2 l 3 l 4 l 5 l 6 1 1 2 2 3 3 3 1100004 0111003 0101102 0001111 1110010 654321 X X X llllll B 00654 05343 05232 03211 65410 4321 ll. X llll. X T Матрица инцидентности: Матрица цепей:

Формальное описание схем (Пример) X 1 (VT 1) X 3 (R 1) X 2 (VT 2) X 4 (R 2) С 02 С 03 С 04 С 01 e 2 l 3 e 4 e 5 e 6 C 11 C 21 C 31 C 41 C 12 C 22 C 32 C 42 C 13 C 23 C 33 C 11 X 1 C 12 C 13 e 2 e 1 X 0 C 04 C 01 C 02 C 03 X 2 C 21 C 22 C 23 e 3 WFCEXG, Часть графа :

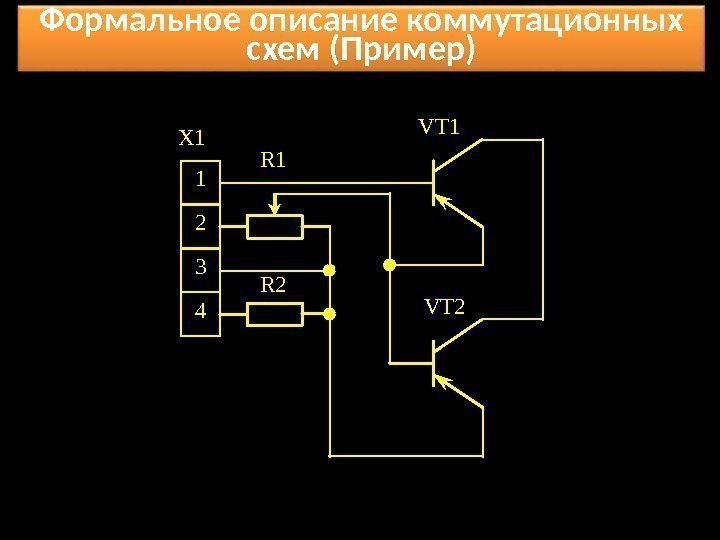
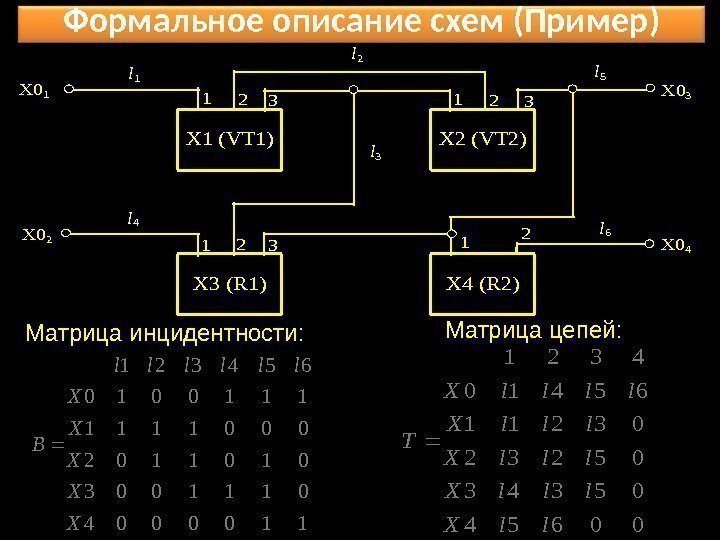
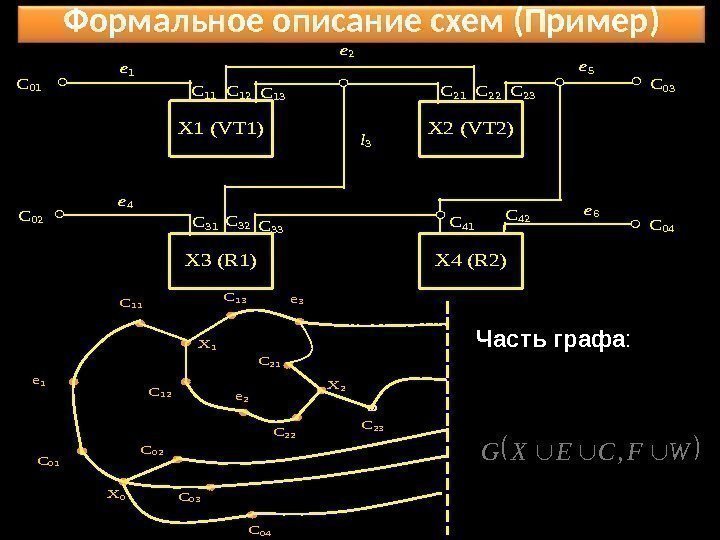
Формальное описание схем (Пример)11 11 111 11 11 6 5 4 3 2 1 4 24 133323123222113121104030201 1 e e e CCCCCCCC A 11 111 1111 4 3 2 1 0 4 24 133323123222113121104030201 2 x x x

Вопрос 3 Основная модель монтажного пространства

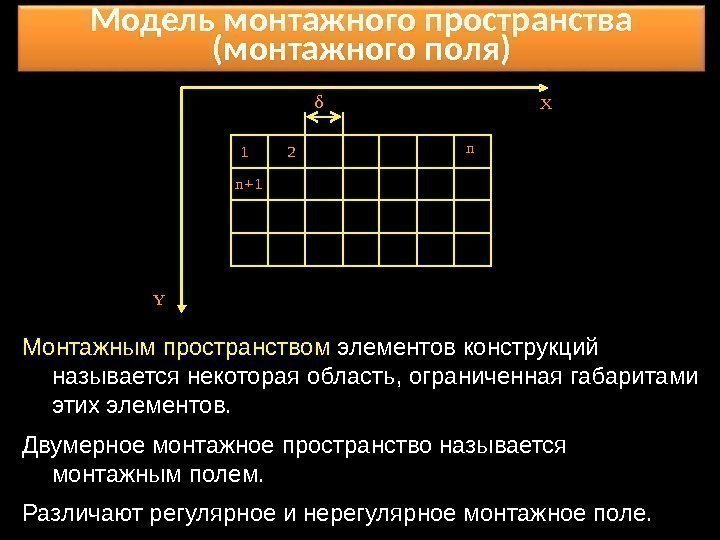
Модель монтажного пространства (монтажного поля) Монтажным пространством элементов конструкций называется некоторая область, ограниченная габаритами этих элементов. Двумерное монтажное пространство называется монтажным полем. Различают регулярное и нерегулярное монтажное поле. Y X δ 1 2 n n+

Модель монтажного пространства Минимальный размер ячейки где h – ширина проводника, s – минимальное расстояние между проводниками. Общее число дискретных ячеек: sh 2 mn. N Место любого i -го дискрета на монтажном поле однозначно может быть указано его координатами (x i , y i ) в системе дискретных координат, либо индексом I nyxiii 1 дискрет → код

Модель монтажного пространства Машинный эквивалент дискретного монтажного поля — двумерный массив B (X, Y) , значения каждого элемента которого соответствуют состоянию дискрета с координатами X, Y, либо одномерный массив B(I). → 0 возрастает класс точности ПП sh

Модель монтажного пространства Аналогично можно поставить в соответствие каждой ячейке вершину графа, тогда модель можно описать графом G (X, U), вершины которого соответствуют вершинам дискретов, а ребра – отображают связи между дискретами. Модель монтажного пространства описывается также матрицей расстояний ( L ij – длина ребра): mn ij d. D нет — если , 0 смежные , если , ijij ij xx. L d

Вопросы по прочитанному материалу?

Спасибо за внимание!