Лекция 15 Электрические заряды Точечный заряд Закон Кулона

Лекция 15 Электрические заряды. Точечный заряд. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции электрических полей. Известно, что при определенных условиях тела приобретают электрический заряд – электризуются. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Электрический заряд является неотъемлемым свойством некоторых элементарных частиц. Заряд всех элементарных частиц одинаков по абсолютной величине (если он не равен нулю). Обозначается он е. Поскольку всякий заряд q образуется совокупностью элементарных зарядов, он является целым кратным e = 1, 602177· 10– 19 Кл ≈ 1, 6· 10– 19 Кл. : Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы о свойствах зарядов:

Электростатика. 15. 2 • 1) Существует два рода электрических зарядов, условно названных положительными и отрицательными. • 2) Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд. • 3) Одноименные заряды отталкиваются, разноименные – притягиваются. Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной: q 1 + q 2 + q 3 +. . . +qn = const Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

Электростатика. 15. 3 • Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. Впервые закон взаимодействия неподвижных зарядов был установлен французским физиком Ш. Кулоном (1785 г. ). С помощью крутильных весов Кулон измерял силу взаимодействия двух заряженных шариков в зависимости от величины зарядов на них и от расстояния между ними. При этом Кулон исходил из того, что при касании заряженного металлического шарика с точно таким же, но не заряженным заряд между ними распределится поровну.

Электростатика. 15. 4 В результате своих опытов Кулон пришел к выводу, что • сила взаимодействия двух точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с проходящей через заряды прямой. Закон кулона может быть выражен следующей формулой В случае одноименных зарядов, сила оказывается положительной (что соответствует отталкиванию между зарядами). В случае разноименных зарядов сила отрицательна (что соответствует притяжению зарядов друг к другу). Закон Кулона можно записать в векторном виде:

Электростатика. 15. 5 По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Для количественного определения электрического поля вводится силовая характеристика – напряженность электрического поля. Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда Напряженность электрического поля – векторная физическая величина. Направление вектора E совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

Электростатика. 15. 6 Как следует из закона Кулона и определения напряженности, напряженность точечного заряда пропорциональна величине заряда q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля: Направлен вектор Е вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.

Электростатика. 15. 7 Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности: Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции.

Электростатика. 15. 8 Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру, и считать, что они “размазаны” определенным образом в пространстве. Другими словами удобно заменить истинное дискретное распределении зарядов фиктивным непрерывным распределением. Такой подход позволяет существенно упростить расчеты, не внося в тоже время значительных ошибок. При переходе к непрерывному распределению, вводят понятие о плотности зарядов (линейной λ, поверхностной σ или объемной ρ): С учетом эти распределений принцип суперпозиции может быть представлен в другой форме:

Электростатика. 15. 9 Зная вектор Е в каждой точке, можно представить электрическое поле наглядно с помощью линий напряженности, или другими словами линий вектора Е. Эти линии проводят так, чтобы касательная к ним в каждой точке совпадала с направлением вектора Е, а густота линий, была бы пропорциональна модулю вектора Е. Кроме того этим линиям приписывают направление, совпадающее с направлением вектора Е. По полученной картине можно легко судить о конфигурации данного электрического поля – о направлении и модуле вектора Е в разных точках поля.

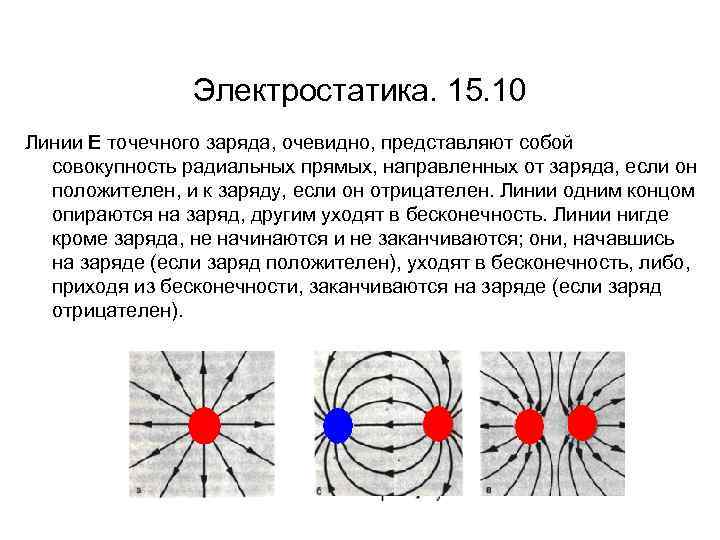Электростатика. 15. 10 Линии Е точечного заряда, очевидно, представляют собой совокупность радиальных прямых, направленных от заряда, если он положителен, и к заряду, если он отрицателен. Линии одним концом опираются на заряд, другим уходят в бесконечность. Линии нигде кроме заряда, не начинаются и не заканчиваются; они, начавшись на заряде (если заряд положителен), уходят в бесконечность, либо, приходя из бесконечности, заканчиваются на заряде (если заряд отрицателен).

Лекция 16 Поток вектора напряженности электрического поля. Теорема Остроградского – Гаусса Поле Е обладает, двумя чрезвычайно важными свойствами, знание которых помогает глубже проникнуть в суть понятия поля и сформулировать его законы, а также открыло возможность решить ряд вопросов весьма просто и изящно. Эти свойства связаны с потоком вектора Е и его циркуляцией. Поток и циркуляция являются двумя важнейшими характеристиками всех векторных полей. Из принципа построения линий напряженности следует, что густота линий Е равна модулю вектора Е. Тогда число линий, пронизывающих элементарную площадку d. S, нормаль n которой составляет угол α с вектором Е, определяется как Ed. Scosα. Эта величина и есть поток d. Ф вектора Е сквозь площадку d. S. В более компактной форме

Электростатика. 16. 2 Выбор направления вектора n условен, его можно было бы направить и в противоположную сторону. Если имеется некоторая произвольная поверхность S то поток вектора Е сквозь нее Эта величина алгебраическая: она зависит не только от конфигурации поля Е, но и от выбора направления нормали. В случае замкнутой поверхности, нормаль принято брать направленной наружу области, области охватываемой этой поверхностью.

Электростатика. 16. 3 Поток вектора напряженности электростатического поля через замкнутую поверхность обладает специфическим свойством: его величина пропорциональна электрическому заряду, расположенному внутри этой поверхности. Это утверждение составляет физический смысл теоремы Гаусса. Доказательство. 1) Допустим, что в начале координат помещен точечный электрический заряд q. Напряженность электрического поля, созданного этим зарядом, описывается соотношением: Окружим заряд q сферой радиуса r, центр которой совпадает с началом координат. Известно, что внешняя нормаль n к элементу поверхности d. S сферы направлена по радиусу

Электростатика. 16. 4 Поток вектора E через поверхность сферы равен: 2)Пусть поверхность S является произвольной достаточно гладкой замкнутой поверхностью, причем начало координат - место расположения заряда q - лежит внутри поверхности S. Заметим, что где α - угол между внешней нормалью n и радусом-вектором r точки, в окрестности которой расположен элемент поверхности d. S; dΩ - элемент телесного угла, под которым виден элемент поверхности d. S из начала координат.

Электростатика. 16. 5 В этом случае прямое вычисление потока вектора E через замкнутую поверхность S приводит к результату Здесь следует иметь ввиду, что для выпуклой замкнутой поверхности S величина d Ω>0 и суммарное значение интеграла в данном выражении равно 4π. Если поверхность S не является строго выпуклой, то для части поверхности cosα>0, а для части поверхности cosα>0, в этом случае d Ω является алгебраической величиной, но в результате все равно получается 4π. Для случая, когда начало координат (т. е. точка расположения заряда q) лежит вне замкнутой поверхности суммарное значение Ω=0, поскольку видимая часть поверхности и невидимая из начала координат часть поверхности приводят к одному и тому же абсолютному значению телесного угла, но противоположных знаков.

Электростатика. 16. 6 3) Реальное электростатическое поле обусловлено совокупностью точечных зарядов (принцип суперпозиции), для каждого из которых соотношение доказано для произвольной замкнутой поверхности S. Но тем самым доказана справедливость теоремы Гаусса для произвольного электростатического поля: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность S равен суммарному электрическому заряду, находящемуся внутри поверхности S, деленному на величину ε 0. Использование теоремы Гаусса в интегральной форме в отдельных случаях, отличающихся высокой степенью симметрии расположения электрических зарядов в пространстве, позволяет эффективно рассчитывать характеристики электростатического поля.

Электростатика. 16. 7 • Поле равномерно заряженной плоскости. Пусть поверхностная плотность заряда равна σ. Из симметрии задачи, очевидно, что вектор Е может быть только перпендикулярным заряженной плоскости. Кроме того, ясно, что в симметричных относительно этой плоскости точках вектор Е одинаков по модулю и противоположен по направлению. Такая конфигурация поля подсказывает, что в качестве замкнутой поверхности следует выбрать прямой цилиндр с основаниями параллельными плоскости. Поток сквозь боковую поверхность этого цилиндра равен нулю, и поэтому полный поток через всю поверхность цилиндра будет 2 EΔS, где ΔS – площадь каждого торца цилиндра. Внутри цилиндра заключен заряд σΔS. Согласно теореме Гаусса 2 EΔS= σΔS откуда получаем:

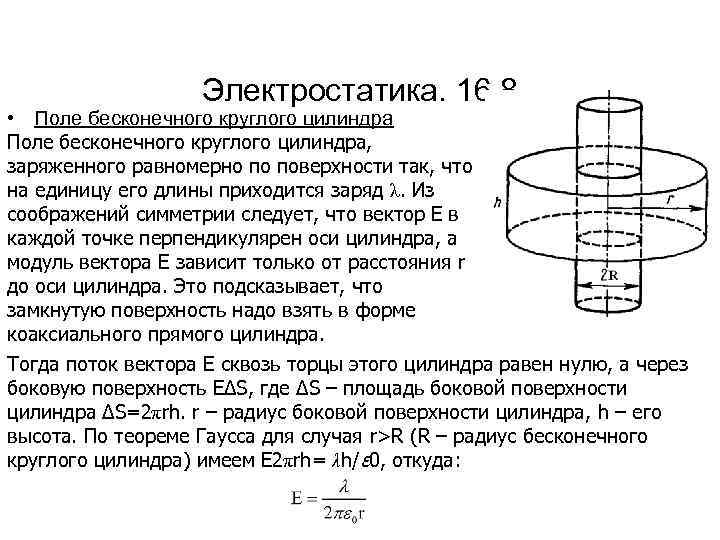Электростатика. 16. 8 Поле бесконечного круглого цилиндра • Поле бесконечного круглого цилиндра, заряженного равномерно по поверхности так, что на единицу его длины приходится заряд λ. Из соображений симметрии следует, что вектор Е в каждой точке перпендикулярен оси цилиндра, а модуль вектора Е зависит только от расстояния r до оси цилиндра. Это подсказывает, что замкнутую поверхность надо взять в форме коаксиального прямого цилиндра. Тогда поток вектора Е сквозь торцы этого цилиндра равен нулю, а через боковую поверхность ЕΔS, где ΔS – площадь боковой поверхности цилиндра ΔS=2πrh. r – радиус боковой поверхности цилиндра, h – его высота. По теореме Гаусса для случая r>R (R – радиус бесконечного круглого цилиндра) имеем Е 2πrh= λh/ε 0, откуда:

Электростатика. 16. 9 • Поле сферической поверхности, заряженной равномерно зарядом q. Это поле центрально-симметрично – направление вектора Е в любой точке проходит через центр сферы, а модуль зависит только от расстояния до центра сферы. При такой конфигурации поля в качестве замкнутой поверхности надо взять концентрическую сферу. Пусть ее радиус r>R, тогда по теореме Гаусса откуда Если r

Электростатика. 16. 10 • Поле сферы заряженной объемной плотностью заряда ρ Поле такой сферы тоже обладает центральной симметрией. Для поля вне сферы получается тот же результат, что и в случае поверхностно заряженной сферы. Однако для точек внутри результат будет другой. Сферическая поверхность радиуса r (r

Лекция 17 Работа сил электростатического поля. Потенциал. Эквипотенциальные поверхности. Связь между напряженностью электрического поля и потенциалом. При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Оказывается, что работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда. Из механики известно, что такое поле называется консервативным. Если в качестве пробного заряда, переносимого из точки 1 в точку 2 поля Е, взять единичный положительный заряд, то элементарная работа сил поля на перемещении dl равна Edl, а вся работа сил поля на пути от точки 1 до точки 2 определяется как Этот интеграл берется по некоторому пути (линии), поэтому его называют линейным.

Электростатика. 17. 2 Интеграл данного вида, взятый по замкнутому пути, называется циркуляцией вектора Е и обозначается Теорема о циркуляции вектора Е гласит: циркуляция вектора Е в любом электростатическом поле равна нулю т. е. Поле, обладающее таким свойством, называется потенциальным. Теорема о циркуляции вектора Е позволяет сделать ряд важных выводов, практически не прибегая к расчетам. Например, линии электростатического поля не могут быть замкнутыми.

Электростатика. 17. 3 Тело находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа сил электростатического поля может быть представлена как разность значений потенциальной энергии, которыми обладал заряд в точках 1 и 2 поля Е. Можно утверждать, что в электростатическом поле существует некоторая скалярная функция координат φ(r), убыль которой Так определенная величина φ(r) называется потенциалом поля. Из сопоставления данного выражения с выражением для работы сил потенциального поля ( которая равна убыли потенциальной энергии частицы в поле) можно сказать, что потенциал – это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля.

Электростатика. 17. 4 Потенциал какой-либо произвольной точки поля определяется с точностью до произвольной аддитивной константы. Элементарная убыль потенциала на dl есть Другими словами, если известно поле E(r), то для нахождения φ надо представить как убыль некоторой функции. Потенциал поля неподвижного точечного заряда: Таким образом, потенциал поля точечного заряда

Электростатика. 17. 5 Если имеется система из N неподвижных точечных зарядов q 1, q 2, …. Согласно принципу суперпозиции в любой точке поля напряженность Е=Е 1+Е 2+…, где Еi – напряженность поля создаваемого отдельно зарядом q 1 и т. д. Тогда можно записать Таким образом, потенциал системы неподвижных точечных зарядов Если заряды, образующие системы, распределены непрерывно, то, каждый элементарный объем d. V содержит точечный заряд ρd. V, где ρ – объемная плотность заряда в месте нахождения объема d. V. Тогда при вычислении потенциала можно перейти от суммирования дискретно распределенных в пространстве зарядов к интегрированию по заряженному объему:

Электростатика. 17. 6 Если заряды расположены только по поверхности S то получаем следующее соотношение: Получили, что электрическое поле можно описывать как с помощью напряженности, так и с помощью потенциала. Следовательно, раз эти две величины описывают одно и то же физическое явление, то между ними должна существовать однозначная связь. Связь между φ и Е можно установить с помощью соотношения Пусть перемещение dl параллельно оси Х, тогда dl=exdx, где ex – орт оси Х; dx – приращение координаты х. В этом случае Получим

Электростатика. 17. 7 Аналогичные рассуждение, позволяют определить Ey, Ez, а зная их легко найти и вектора напряженности электрического поля Е: Величина, стоящая в скобках есть градиент потенциала φ (grad φ или φ). Окончательно связь вектора Е и потенциала φ выглядит следующим образо Распределение потенциала в пространстве наглядно изображают с помощью эквипотенциальных поверхностей – поверхностей во всех точках, которых потенциал имеет одно и то же значение.

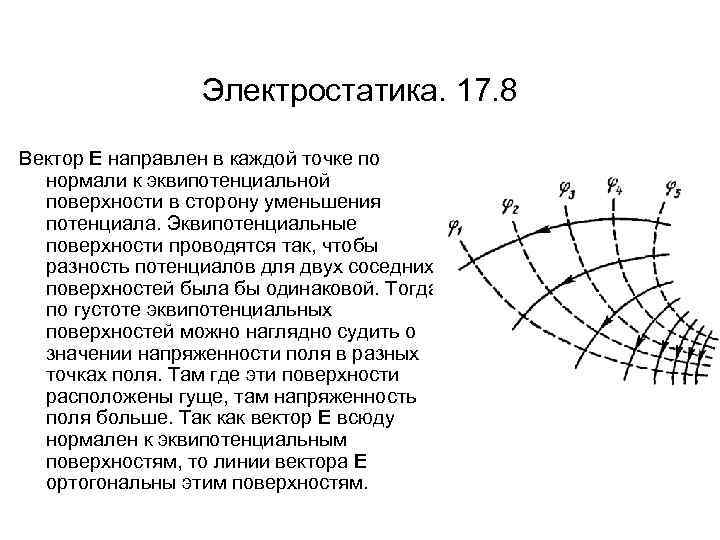Электростатика. 17. 8 Вектор Е направлен в каждой точке по нормали к эквипотенциальной поверхности в сторону уменьшения потенциала. Эквипотенциальные поверхности проводятся так, чтобы разность потенциалов для двух соседних поверхностей была бы одинаковой. Тогда по густоте эквипотенциальных поверхностей можно наглядно судить о значении напряженности поля в разных точках поля. Там где эти поверхности расположены гуще, там напряженность поля больше. Так как вектор Е всюду нормален к эквипотенциальным поверхностям, то линии вектора Е ортогональны этим поверхностям.

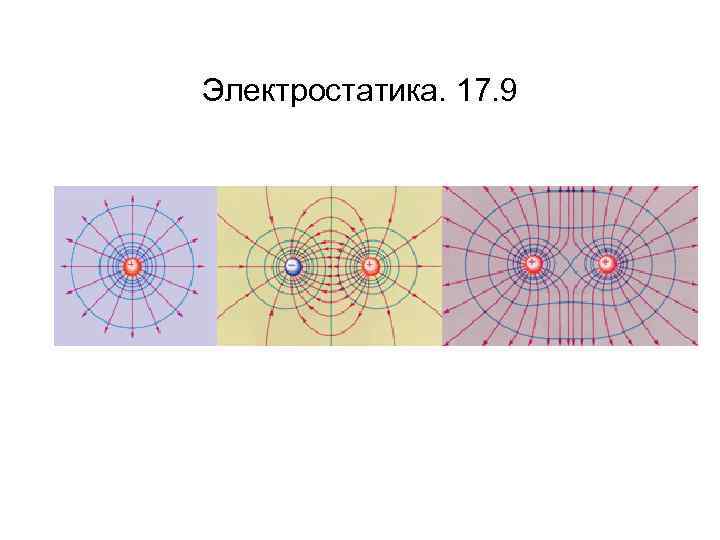Электростатика. 17. 9

Электростатика. 17. 10 1) Зная потенциал φ(r), можно предельно просто вычислить работу сил поля приперемещении точечного заряда из точки 1 в точку 2 2) Во многих случаях оказывается, что для нахождения напряженности Е электрического поля легче сначала подсчитать потенциал и затем взять градиент от него, чем непосредственно вычислять Е. Действительно, для вычисления φ нужно взять один интеграл, а для вычисления Е – три (так как Е вектор).

Лекция 18 Поле В. Сила Лоренца. Закон Био – Савара. Циркуляция и поток вектора В. Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. Он появился в Европе приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле. Первыми экспериментами, показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда (1820 г. ). Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся повернуть стрелку.

Магнитное поле в вакууме 18. 2 В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов. По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля. Все свойства магнитной силы можно описать, если ввести понятие магнитного поля. Это поле характеризуется магнитной индукцией В. Магнитное поле действует на движущейся электрический заряд с силой Тогда полная электромагнитная сила, действующая на заряд q: ее называют силой Лоренца. Она состоит из электрической и магнитной составляющих.

Магнитное поле в вакууме 18. 3 Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость v лежит в плоскости, перпендикулярной вектору B то частица будет двигаться по окружности радиуса Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости v и радиуса траектории R. Угловая скорость движения заряженной частицы по круговой траектории: Называется циклотронной частотой.

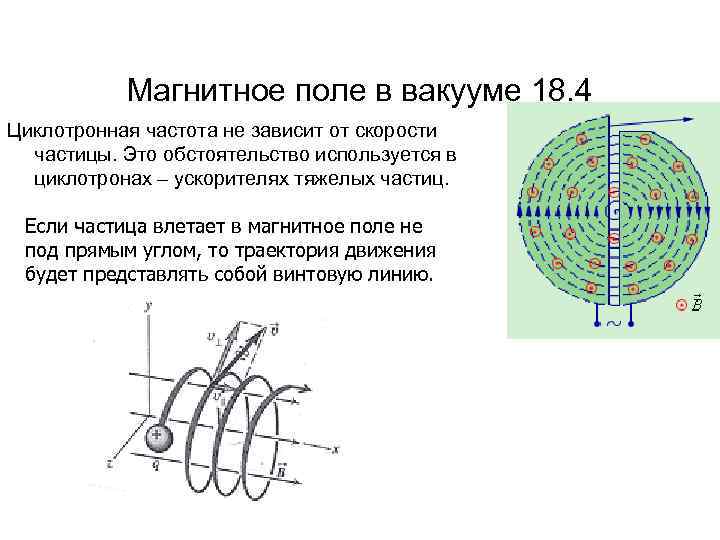Магнитное поле в вакууме 18. 4 Циклотронная частота не зависит от скорости частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц. Если частица влетает в магнитное поле не под прямым углом, то траектория движения будет представлять собой винтовую линию.

Магнитное поле в вакууме 18. 5 Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера). В результате обобщения экспериментальных данных был получен элементарный закон, определяющий поле В точечного заряда q, движущегося с постоянной нерелятивистской скоростью v. Этот закон записывается в виде: μ 0 – магнитная постоянная.

Магнитное поле в вакууме 18. 6 Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г. ). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности. Пусть магнитное поле создается постоянным электрическим током, тогда выделив в этом токе точечный движущейся заряд а затем просуммировав все эти элементарные заряды, можно найти магнитное поле В, создаваемое данным током.

Магнитное поле в вакууме 18. 7 Элементарный заряд q равен ρd. V, где d. V – элементарный объем, ρ – объемная плотность заряда, являющегося носителем тока, учтем также, что ρv=j плотность тока. Тогда магнитное поле, создаваемое таким зарядом равно: Магнитное поле создаваемое линейным элементом тока выглядит следующим образом: Полное поле В в соответствии с принципом суперпозиции находим интегрированием этих выражений по всем элементам тока

Магнитное поле в вакууме 18. 8 Как и любое другое векторное поле, поле В может быть представлено наглядно с помощью лини вектора В. Их проводят обычным способом – так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора В, а густота линий была бы пропорциональна модулю вектора В в данном месте. Магнитное поле обладает, как и электрическое поле, двумя важнейшими свойствами – поток и циркуляция вектора В. Поток вектора В сквозь любую замкнутую поверхность равен нулю : Равенство потока вектора В нулю также является следствием того, что в природе не существует магнитных зарядов на которых начинались бы или заканчивались линии магнитной индукции В.

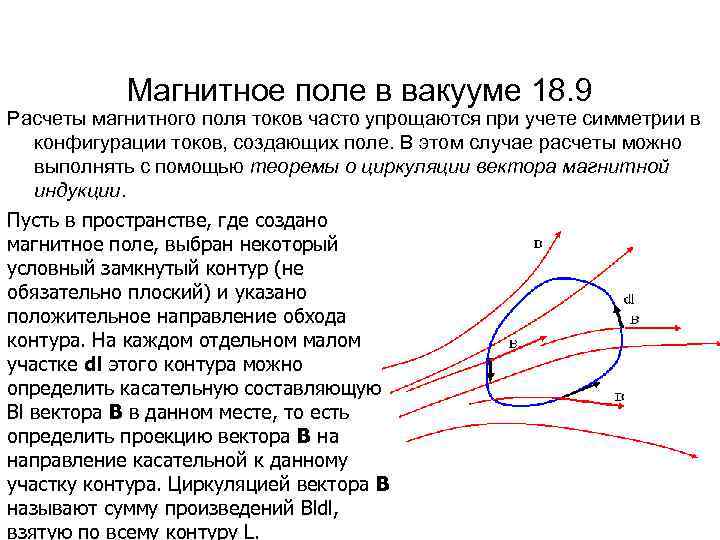Магнитное поле в вакууме 18. 9 Расчеты магнитного поля токов часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае расчеты можно выполнять с помощью теоремы о циркуляции вектора магнитной индукции. Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление обхода контура. На каждом отдельном малом участке dl этого контура можно определить касательную составляющую Bl вектора B в данном месте, то есть определить проекцию вектора B на направление касательной к данному участку контура. Циркуляцией вектора В называют сумму произведений Bldl, взятую по всему контуру L.

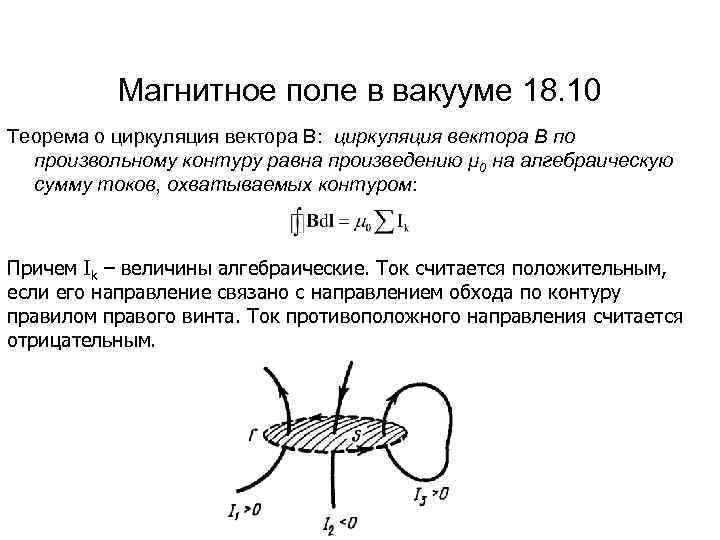Магнитное поле в вакууме 18. 10 Теорема о циркуляция вектора В: циркуляция вектора В по произвольному контуру равна произведению μ 0 на алгебраическую сумму токов, охватываемых контуром: Причем Ik – величины алгебраические. Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта. Ток противоположного направления считается отрицательным.

Лекция 19 Применение теоремы о циркуляции вектора В. Поле прямого тока. Применение теоремы о циркуляции вектора В. Поле соленоида. • Магнитно поле прямого тока. Пусть постоянный ток I течет вдоль бесконечно длинного прямого провода, имеющего круглое сечение радиуса а. Необходимо найти индукцию В поля снаружи и внутри провода. Из симметрии задачи следует, что линии вектора В в данном случае должны иметь вид окружностей с центром на оси провода. Причем модуль вектора В должен быть одинаков во всех точках на расстоянии r от оси провода. Поэтому по теореме о циркуляции вектора В для круглого контура , откуда следует, что вне провода (r>a).

Магнитное поле в вакууме 19. 2 Внутри провода из тех же соображений симметрии следует, что линии вектора В являются тоже окружностями. Поэтому выбираем контур виде окружности. По теореме о циркуляции для контура внутри провода где Ir – ток, охватываемый контуром . Он пропорционален площади охватываемой контуром. Отсюда находим, что внутри провода:

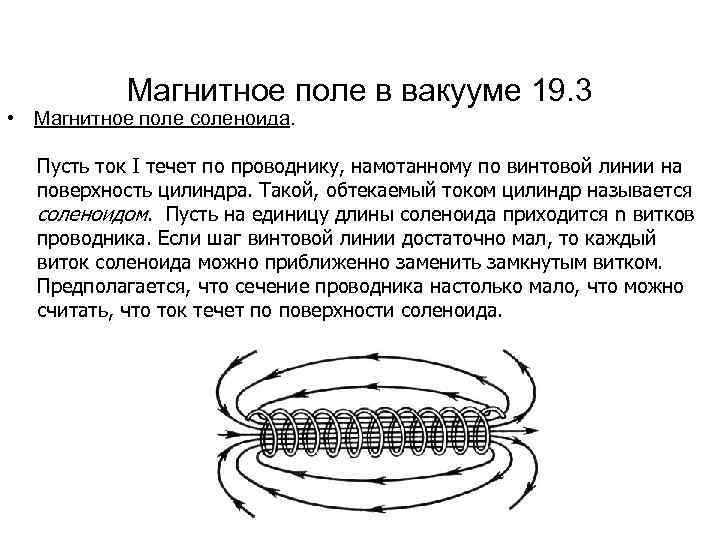Магнитное поле в вакууме 19. 3 • Магнитное поле соленоида. Пусть ток I течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой, обтекаемый током цилиндр называется соленоидом. Пусть на единицу длины соленоида приходится n витков проводника. Если шаг винтовой линии достаточно мал, то каждый виток соленоида можно приближенно заменить замкнутым витком. Предполагается, что сечение проводника настолько мало, что можно считать, что ток течет по поверхности соленоида.

Магнитное поле в вакууме 19. 4 Опыт показывает на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида. Из соображений симметрии ясно, что линии вектора В внутри соленоида направлены вдоль его оси, причем вектор В составляет с направлением тока правовинтовую систему. Такая конфигурация линий поля подсказывает выбрать контур в виде прямоугольника, две стороны которого параллельны линиям поля, причем одна из них находится вне соленоида. Вторые две стороны оказываются перпендикулярны линиям магнитной индукции.

Магнитное поле в вакууме 19. 5 В итоге получаем, что циркуляция по трем из четырех сторон прямоугольника равна нулю. По стороне вне соленоида, так как там нет поля. По сторонам перпендикулярным полю, так как проекция линий поля на них равна нулю. Тогда согласно теореме о циркуляции получаем где l - длина стороны параллельной линиям магнитной индукции. Окончательно получаем, поле внутри длинного соленоида имеет вид: Т. е. поле внутри длинного соленоида однородно (за исключением областей, прилегающих к торцам соленоида). Произведение n. I называют числом ампервитков.

Магнитное поле в вакууме 19. 6 • Магнитное поле тороида. Тороид представляет собой провод, навитый на каркас, имеющий форму тора. Предполагается, что катушка по которой течет ток I плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. Из соображений симметрии можно понять, что линии вектора В должны быть окружностями, центры которых расположены на оси тороида. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Поэтому ясно, что в качестве контура следует взять одну из таких окружностей.

Магнитное поле в вакууме 19. 7 Если контур расположен внутри тороида, то он охватывает N витков с током (N – число витков в тороидальной катушке). Тогда количество токов охватываемых контуром радиуса r равно NI. Следовательно, по теореме о циркуляции получаем , откуда следует, что внутри тороида Если выбранный нами круглый контур проходит вне тороида, то токов он не охватывает, поэтому для такого контура. Это значит, что вне тороида магнитное поле отсутствует.

Магнитное поле в вакууме 19. 8 • Магнитное поле плоскости с током. Рассмотрим безграничную проводящую плоскость, по которой течет равномерно распределенный ток одного направления. Введем понятие линейной плотности тока как вектор i, направленный вдоль линий тока. Модуль этого вектора представляет собой ток, приходящийся на единицу длины, которая играет роль поперечного сечения. Разбив мысленно плоскость с током на тонкие нити с током, нетрудно видеть, что результирующее поле В будет направлено параллельно плоскости, причем направление с разных сторон плоскости будет различным и определяться по правилу правого винта.

Магнитное поле в вакууме 19. 9 Зная, как расположены в этом случае линии вектора В, выберем контур в виде прямоугольника. Две стороны, которого параллельны плоскости, а две перпендикулярны. Тогда циркуляция вектора В по перпендикулярным сторонам будет равна нулю, так как проекция вектора В на них равна нулю. Следовательно по теореме о циркуляции получаем В итоге находим Магнитное поле как с одной стороны плоскости, так и с другой является однородным. Этот результат справедлив и для ограниченной пластины с током, но лишь на расстояниях близких к пластине и удаленных от ее краев.

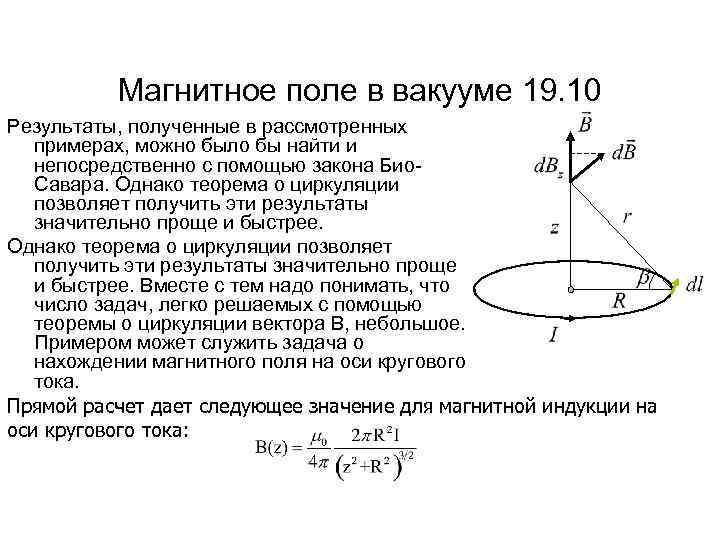Магнитное поле в вакууме 19. 10 Результаты, полученные в рассмотренных примерах, можно было бы найти и непосредственно с помощью закона Био. Савара. Однако теорема о циркуляции позволяет получить эти результаты значительно проще и быстрее. Вместе с тем надо понимать, что число задач, легко решаемых с помощью теоремы о циркуляции вектора В, небольшое. Примером может служить задача о нахождении магнитного поля на оси кругового тока. Прямой расчет дает следующее значение для магнитной индукции на оси кругового тока:

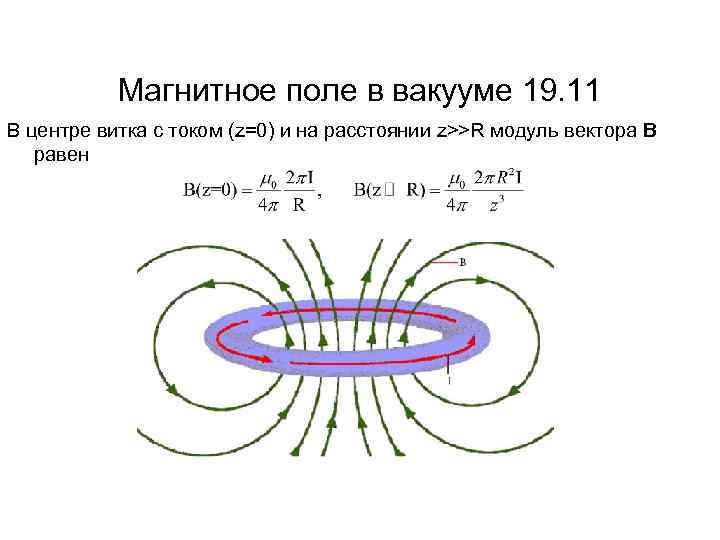Магнитное поле в вакууме 19. 11 В центре витка с током (z=0) и на расстоянии z>>R модуль вектора В равен

Лекция 20 Сила Ампера. Работа поля В при перемещении контура стоком. Каждый носитель тока испытывает действие магнитной силы. Действие этой силы передается проводнику, по которому движутся заряды. В результате магнитное поле действует с определенной силой на сам проводник с током. Пусть объемная плотность заряда, являющегося носителем тока равна ρ. Выделим мысленно элемент объема d. V проводника. В нем находится заряд – носитель тока, равный ρd. V. Тогда сила, действующая на элемент d. V проводника, может быть записана в виде: Так как Закон Ампера Если ток течет по тонкому проводнику, то так как Закон Ампера получим

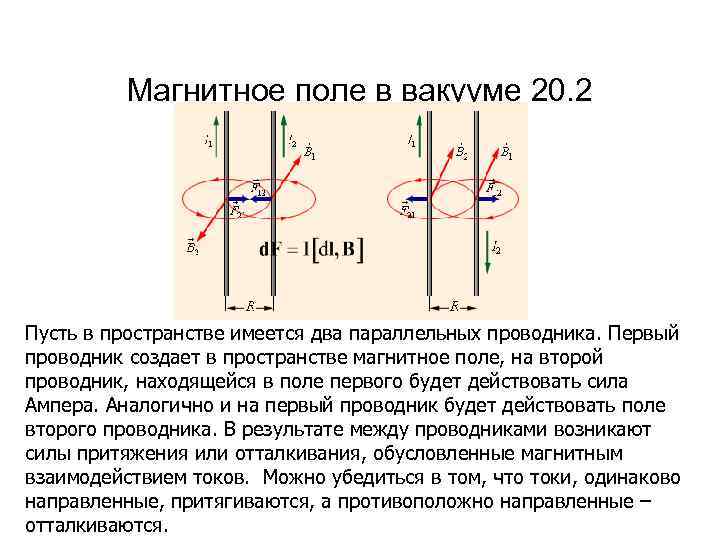Магнитное поле в вакууме 20. 2 Пусть в пространстве имеется два параллельных проводника. Первый проводник создает в пространстве магнитное поле, на второй проводник, находящейся в поле первого будет действовать сила Ампера. Аналогично и на первый проводник будет действовать поле второго проводника. В результате между проводниками возникают силы притяжения или отталкивания, обусловленные магнитным взаимодействием токов. Можно убедиться в том, что токи, одинаково направленные, притягиваются, а противоположно направленные – отталкиваются.

Магнитное поле в вакууме 20. 3 Результирующая сила Ампера, которая действует на контур с током в магнитном поле, определяется следующим образом: Где интегрирование проводится по всему данному контуру с током. Если магнитное поле однородно, то вектор В можно вынести из-под интеграла и задача сводится к вычислению векторного интеграла Этот интеграл представляет собой замкнутую цепочку элементарных векторов dl, поэтому он равен нулю. Значит и F=0, т. е. результирующая сила Ампера равна нулю в однородном магнитном поле. Если магнитное поле неоднородно, то результирующая сила отлична от нуля и определяется с помощью интегрирования.

Магнитное поле в вакууме 20. 4 Поведение элементарного контура с током удобно описывать с помощью магнитного момента pm. По определению Подробный расчет по формуле с учетом малости контура приводи к следующему выражению для силы, действующей на элементарный контур с током в неоднородном магнитном поле: – производная вектора В по направлению нормали n или по направлению вектора pm.

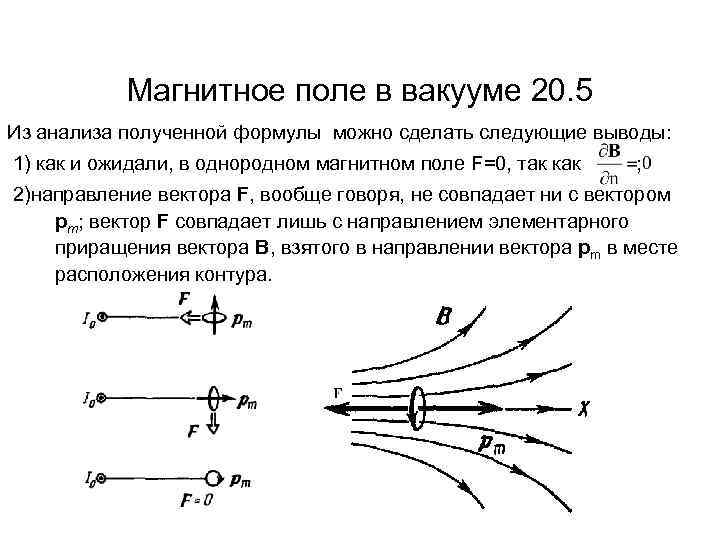Магнитное поле в вакууме 20. 5 Из анализа полученной формулы можно сделать следующие выводы: 1) как и ожидали, в однородном магнитном поле F=0, так как ; 2)направление вектора F, вообще говоря, не совпадает ни с вектором pm; вектор F совпадает лишь с направлением элементарного приращения вектора B, взятого в направлении вектора pm в месте расположения контура.

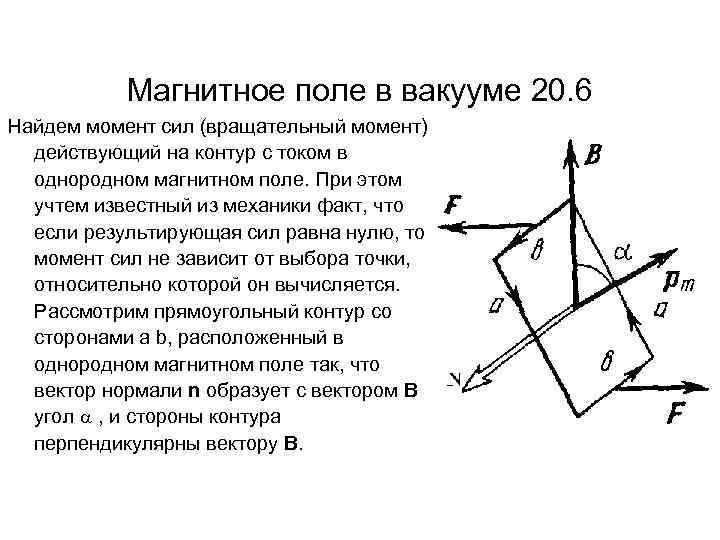Магнитное поле в вакууме 20. 6 Найдем момент сил (вращательный момент), действующий на контур с током в однородном магнитном поле. При этом учтем известный из механики факт, что если результирующая сил равна нулю, то момент сил не зависит от выбора точки, относительно которой он вычисляется. Рассмотрим прямоугольный контур со сторонами a b, расположенный в однородном магнитном поле так, что вектор нормали n образует с вектором В угол , и стороны контура перпендикулярны вектору В.

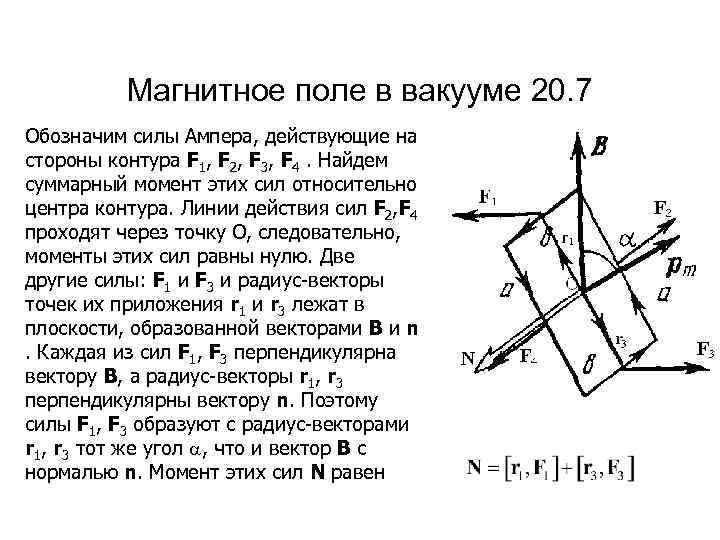Магнитное поле в вакууме 20. 7 Обозначим силы Ампера, действующие на стороны контура F 1, F 2, F 3, F 4. Найдем суммарный момент этих сил относительно центра контура. Линии действия сил F 2, F 4 проходят через точку О, следовательно, моменты этих сил равны нулю. Две другие силы: F 1 и F 3 и радиус-векторы точек их приложения r 1 и r 3 лежат в плоскости, образованной векторами B и n. Каждая из сил F 1, F 3 перпендикулярна вектору В, а радиус-векторы r 1, r 3 перпендикулярны вектору n. Поэтому силы F 1, F 3 образуют с радиус-векторами r 1, r 3 тот же угол , что и вектор B с нормалью n. Момент этих сил N равен

Магнитное поле в вакууме 20. 8 Слагаемые в этой сумме направлены в одну сторону. По формуле (для силы Ампера) обе силы равны F 1=F 2=Ia. B, кроме того, r 1=r 2=a/2. Поэтому слагаемые одинаковы по величине и равны а величина результирующего момента Воспользовавшись определением магнитного момента контура, можно записать величину момента сил Ампера, действующих на этот контур: Векторы pm, B, N составляют правую тройку векторов, поэтому в общем виде получаем

Магнитное поле в вакууме 20. 9 Для момента сил Ампера, существует два положения = 0 и = , в которых этот момент обращается в нуль. В остальных случаях вращающий момент, действующий на контур с током, стремится развернуть контур так, чтобы направление магнитного момента контура совпало с направлением магнитной индукции внешнего поля, т. е. к состоянию = 0. Поэтому при = 0 контур оказывается в устойчивом равновесии, а при = – в неустойчивом. Элементарная работа d. А, совершаемая силой Ампера d. F при перемещении на dr в магнитном поле элемента проводника dl, равна Векторное произведение перемещения и элемента проводника есть вектор площадки, прочерченной проводником при его перемещении

Магнитное поле в вакууме 20. 10 Скалярное произведение вектора площадки и вектора магнитной индукции – это магнитный поток через площадку d. S поэтому для работы получаем Если проводник, сила тока I в котором поддерживается постоянной, совершает конечное перемещение из положения 1 в положение 2, то работа сил Ампера при таком перемещении где Ф – магнитный поток через поверхность, прочерченную проводником при рассматриваемом перемещении.

Магнитное поле в вакууме 20. 11 Если в постоянном магнитном поле перемещается замкнутый контур, то поток, прочерченный всеми элементами контура, равен изменению потока пронизывающего контур. Предположим есть два последовательных состояния контура С 1 и С 2. Поверхности S 1 и S 2, которые ограничивает контур в положениях С 1 и С 2 и поверхность Sп, прочерченная контуром, составляют замкнутую поверхность. По теореме Остроградского-Гаусса для магнитной индукции суммарный поток через эту замкнутую поверхность равен нулю. Выберем нормали n 1 и n 2 к поверхностям S 1 и S 2. При этом поток наружу из замкнутой поверхности складывается из потока через S 1 в направлении n 1 (равен Ф 1), потока через S 2 в направлении противоположном n 2 (равен Ф 2) и потока через прочерченную поверхность Sп (Ф). Таким образом, получаем

Магнитное поле в вакууме 20. 12 откуда Ф=Ф 2 -Ф 1. Следовательно, соотношение для замкнутого контура можно записать так При выводе этой формулы мы рассмотрели простое перемещение контура, но она оказывается справедливой и при более сложных изменениях состояния контура, например, при вращении и при деформации. В приведенном виде она выполняется для движении не только одиночного контура, но и катушки, состоящей из нескольких витков, в частности, для катушки из N одинаковых витков. В последнем случае потокосцепление равно = N м, где м – магнитный поток через один виток.

Лекция 21 Виды поляризации диэлектриков. Поляризованность Р. Свойства поля вектора Р. Вектор D. Условия на границе двух диэлектриков для векторов E и D Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. В диэлектриках нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика. При внесении диэлектрика во внешнее электрическое поле Е 0 в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности и, вообще говоря, и в объеме диэлектрического образца появляются избыточные нескомпенсированные связанные заряды.

Диэлектрики 21. 2 Связанные заряды создают электрическое поле Е’ которое внутри диэлектрика направлено противоположно вектору напряженности Е 0 внешнего поля. Этот процесс называется поляризацией диэлектрика. Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная и электронная поляризации. Первый механизм работает при поляризации полярных диэлектриков, второй – неполярных.

Диэлектрики 21. 3 Каждый малый объем d. V (малый по сравнению с объемом диэлектрического тела, но большой по сравнению с объемом молекулы, атома или элементарной ячейки кристалла) приобретает дипольный момент pi– дипольные моменты молекул Дипольным моментом диполя(молекулы) называется векторная величина: Вектор l направлен от –q к +q Векторная величина называемая поляризованностью (численно равная дипольному моменту единичного объема диэлектрической среды) не зависит от d. V.

Диэлектрики 21. 4 Для диэлектриков зависимость поляризованности от напряженности электрического поля линейна: - безразмерная величина, называемая диэлектрической восприимчивостью вещества. Эта величина не зависит от Е она характеризует свойства самого диэлектрика. Поле вектора Р обладает следующим свойством: поток вектора Р сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S Это уравнение выражает теорему Гаусса для вектора Р.

Диэлектрики 21. 5 Поскольку источниками поля Е являются все электрические заряды – сторонние и связанные, теорему Гаусса для поля Е можно записать так: Появление связанных зарядов q’ усложняет дело, и данная формула оказывается мало применима для нахождения поля Е в диэлектрике. Если выразить связанный заряд через поток вектора Р, тогда выражение для потока вектора Е можно преобразовать к следующему виду: Величину, стоящую под интегралом в скобках, обозначают буквой D. В итоге получили вспомогательный вектор D:

Диэлектрики 21. 6 Поток вектора D сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью: В случае изотропных диэлектриков поляризованность Для вектора D получим ε – диэлектрическая проницаемость вещества: Диэлектрическая проницаемость является основной электрической характеристикой диэлектрика. Для всех веществ ε>0, для вакуума ε=0. В изотропных диэлектриках вектор D коллинеарен вектору Е. Поле вектора D наглядно можно изобразить с помощью линий вектора D, направление и густота которых определяется точно так же как и у линий вектора Е. Однако линии D могут начинаться или заканчиваться только на сторонних заряда или на бесконечности.

Диэлектрики 21. 7 Рассмотрим поведение векторов E и D на границе раздела двух однородных изотропных диэлектриков. Предположим, что на границе раздела этих диэлектриков находится поверхностный сторонний заряд σ. Условия для E и D получим, используя теорему о циркуляции вектора Е и о потоке D. Возьмем небольшой вытянутый прямоугольный контур, ориентировав его следующим образом В результате получаем граничные условия, для тангенциальной составляющей вектора Е

Диэлектрики 21. 8 Возьмем очень малой высоты цилиндр, расположив его на границе раздела двух диэлектриков. 2 1 Сечение цилиндра должно быть таким, чтобы в пределах каждого его торца вектор D был одинаков. Тогда согласно теореме Гаусса для вектора D Взяв обе проекции вектора D на общую нормаль получим => Из этого соотношения видно, что нормальная составляющая вектора D претерпевает скачок при переходе границы раздела Однако если сторонние заряды на границе раздела отсутствуют =>

Диэлектрики 21. 9 Если на границе раздела нет сторонних зарядов то получаем В этом случае при переходе границы, составляющие Еτ и Dn скачок не испытывают. Составляющие же Еn и Dτ претерпевают скачок. Полученные результаты позволяют построить линии этих векторов при переходе из одного диэлектрика в другой.

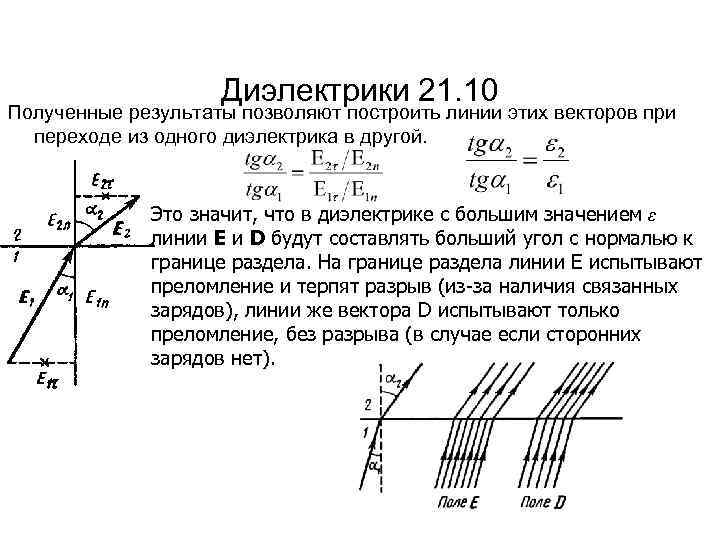Диэлектрики 21. 10 Полученные результаты позволяют построить линии этих векторов при переходе из одного диэлектрика в другой. Это значит, что в диэлектрике с большим значением ε линии Е и D будут составлять больший угол с нормалью к границе раздела. На границе раздела линии Е испытывают преломление и терпят разрыв (из-за наличия связанных зарядов), линии же вектора D испытывают только преломление, без разрыва (в случае если сторонних зарядов нет).

Лекция 22 Намагничение вещества. Намагниченность J. Циркуляция вектора J. Вектор Н. Граничные условия для В и Н. Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме. Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками.

Магнетики 22. 2 При описании магнитного поля в веществе – магнетите можно, не вдаваясь в природу этих элементарных токов, для простоты считать их все одинаковыми. Пусть каждая молекула вещества характеризуется некоторым магнитным моментом Количественной характеристикой намагниченного состояния вещества служит векторная величина намагниченность J, равная отношению магнитного момента pm макроскопически малого объёма V вещества к этому объему:

Магнетики 22. 3 Аналогично тому, как это было сделано для поляризованности Р, намагниченность можно выразить как Намагничивание приводит к преимущественной ориентации магнитных моментов молекул. То же самое можно сказать и об элементарных токах. Преимущественная ориентация элементарных токов приводит к возникновению макроскопических токов – токов намагничивания. Обычные токи, связанные с перемещением в веществе носителей тока называются токами проводимости.

Магнетики 22. 4 Оказывается, что для стационарного случая циркуляция намагниченности J по произвольному замкнутому контуру равна алгебраической сумме токов намагничивания I’, охватываемых контуром: В магнетиках, помещенных во внешнее магнитное поле, возникают токи намагничивания, поэтому циркуляция вектора В определяется не только токами проводимости, но и токами намагничивания: Однако оказывается можно найти вспомогательный вектор, циркуляция которого определяется только токами проводимости, охватываемыми контуром. Проведем следующие преобразования:

Магнетики 22. 5 Величину, стоящую под интегралом в скобках обозначают буквой Н – напряженность магнитного поля. В итоге мы нашли некоторый вспомогательный вектор Циркуляция которого по произвольному контуру равна алгебраической сумме токов проводимости I, охватываемых этим контуром: Эта формула выражает теорему о циркуляции вектора Н В случае многих однородных изотропных веществ, как показывает эксперимент, между намагниченностью и вектором Н есть прямая пропорциональность

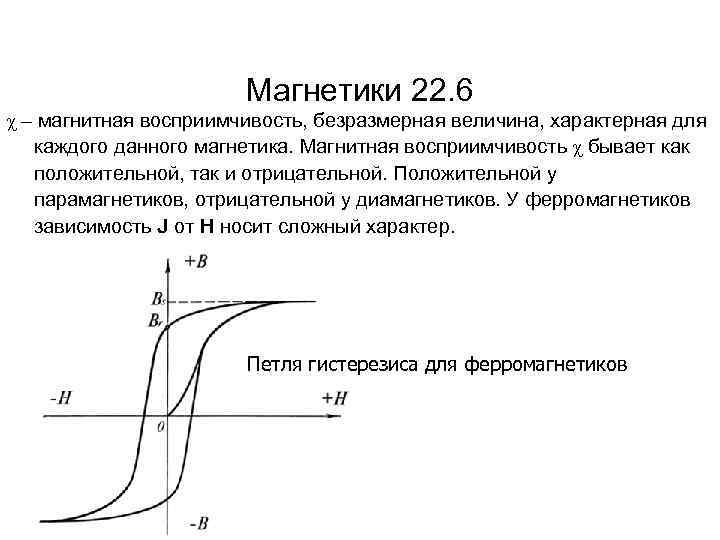Магнетики 22. 6 χ – магнитная восприимчивость, безразмерная величина, характерная для каждого данного магнетика. Магнитная восприимчивость χ бывает как положительной, так и отрицательной. Положительной у парамагнетиков, отрицательной у диамагнетиков. У ферромагнетиков зависимость J от Н носит сложный характер. Петля гистерезиса для ферромагнетиков

Магнетики 22. 7 n Почти все вещества подчиняются зависимости могут быть разбиты на два класса: n n – парамагнетики, в которых намагниченность вещества увеличивает суммарное магнитное поле; , они втягиваются в область сильного неоднородного магнитного поля. – диамагнетики, в которых намагниченность уменьшает суммарное поле; диамагнетики выталкиваются из области сильного неоднородного поля.

Магнетики 22. 8 В результате можно получить взаимосвязь векторов В и Н. μ – магнитная восприимчивость среды: Найдем соотношение между магнитной индукцией B и напряженностью H магнитного поля в некоторой точке А на границе двух сред. Проведем в точке А единичные векторы: – по касательной вдоль границы раздела сред и n – по нормали к границе, направленной от первой среды ко второй. Построим вблизи точки А небольшой замкнутый прямоугольный контур L, две стороны которого параллельны вектору и равны l, а две - вектору n и равны h. Предположим, что по границе раздела внутри контура вблизи точки А не текут макротоки. Из теоремы о циркуляции вектора напряженности магнитного поля следует, что

Магнетики 22. 9 Это равенство должно выполняться при любом значении h и тогда в пределе при получаем Здесь H 1 и H 2 - проекции напряженности H на направление касательного орта в точке А. Поскольку последнее равенство в должно выполняться при произвольном l, находим Таким образом, касательная к поверхности раздела двух сред составляющая напряженности магнитного поля не изменяется при переходе из одной среды в другую.

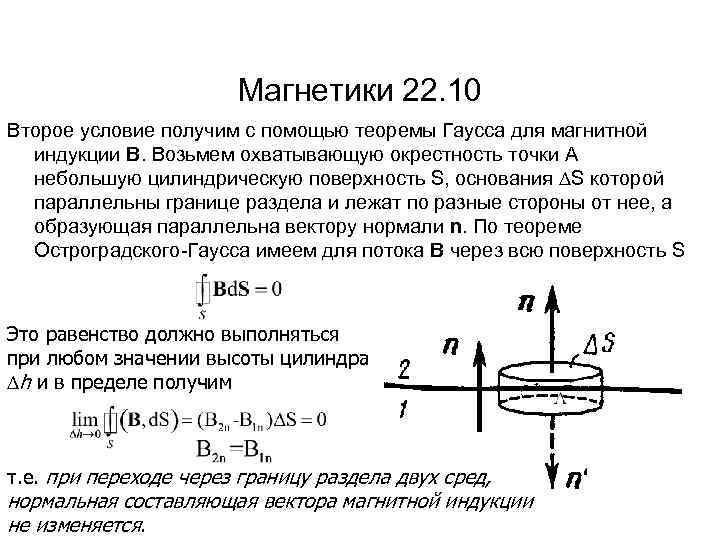Магнетики 22. 10 Второе условие получим с помощью теоремы Гаусса для магнитной индукции B. Возьмем охватывающую окрестность точки А небольшую цилиндрическую поверхность S, основания S которой параллельны границе раздела и лежат по разные стороны от нее, а образующая параллельна вектору нормали n. По теореме Остроградского-Гаусса имеем для потока В через всю поверхность S Это равенство должно выполняться при любом значении высоты цилиндра h и в пределе получим т. е. при переходе через границу раздела двух сред, нормальная составляющая вектора магнитной индукции не изменяется.

Магнетики 22. 11 Используя полученные граничные условия для векторов В и Н и связь между ними, найдем ход линий этих векторов при переходе границы раздела, в случае отсутствия токов проводимости Отношение тангенсов углов α 1 и α 2 углов Линии В не терпят разрыва при переходе границы, линии же Н терпят разрыв (из-за поверхностных токов намагничивания).

Лекция 23 Законы геометрической оптики. Принцип Ферма. Явление полного отражения. Основные законы геометрической оптики были известны задолго до установления физической природы света. Исторически эти законы были открыты намного раньше, чем была понята электромагнитная природа света. Первые три закона были известны Евклиду, Аристотелю. Закон преломления был открыт в 17 в. Синелиусом и Декартом. Границы применимости геометрической оптики 1. Когда характерные поперечные размеры пучков света достаточно велики по сравнению с длиной волны, можно пренебречь расходимостью пучка света и считать, что он распространяется в одном единственном направлении: вдоль светового луча 2. Кроме отсутствия волновых эффектов, в геометрической оптике пренебрегают также квантовыми эффектами. 3. Кроме того, как правило, не рассматриваются эффекты, связанные с откликом среды на прохождение лучей света. Эффекты такого рода, даже формально лежащие в рамках геометрической оптики, относят к нелинейной оптике

Геометрическая оптика 23. 2 1. Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров ( «точечный источник» ). 2. Независимость световых лучей заключается в том, что они при пересечении не возмущают друга. Пересечения лучей не мешают каждому из них распространяться независимо друг от друга.

Геометрическая оптика 23. 3 На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а частично пройти через границу и распространяться во второй среде. Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

Геометрическая оптика 23. 4 Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред равная относительному показателю преломления. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: Физический смысл относительного показателя преломления – это отношение скорости распространения волн в первой среде υ1 к скорости их распространения во второй среде υ2:

Геометрическая оптика 23. 4 Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света v в среде: Закон обратимости (или взаимности) световых лучей: если навстречу лучу, претерпевшему ряд отражений и преломлений, пустить другой луч, то он пойдет по тому же пути, что и первый (прямой) луч, но в обратном направлении

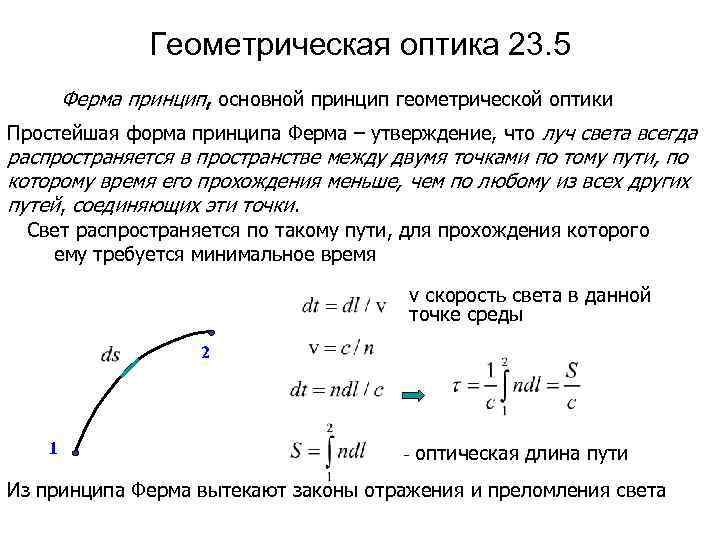Геометрическая оптика 23. 5 Ферма принцип, основной принцип геометрической оптики Простейшая форма принципа Ферма – утверждение, что луч света всегда распространяется в пространстве между двумя точками по тому пути, по которому время его прохождения меньше, чем по любому из всех других путей, соединяющих эти точки. Свет распространяется по такому пути, для прохождения которого ему требуется минимальное время v скорость света в данной точке среды 2 1 - оптическая длина пути Из принципа Ферма вытекают законы отражения и преломления света

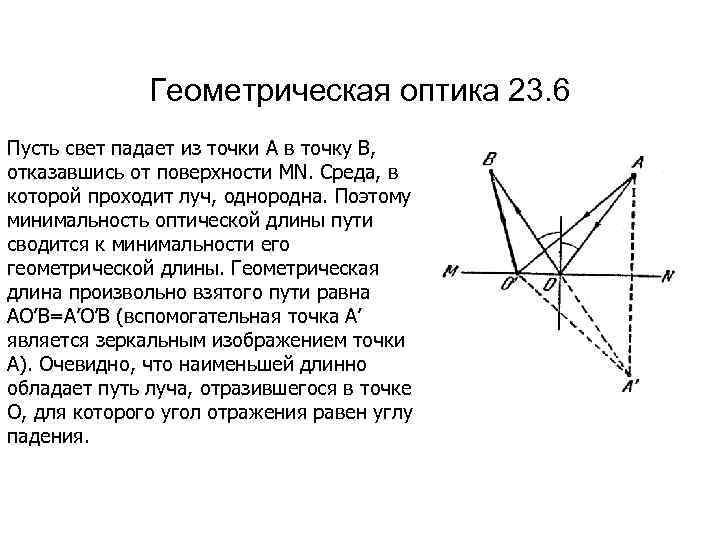Геометрическая оптика 23. 6 Пусть свет падает из точки А в точку В, отказавшись от поверхности MN. Среда, в которой проходит луч, однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины. Геометрическая длина произвольно взятого пути равна АО’В=А’О’В (вспомогательная точка А’ является зеркальным изображением точки А). Очевидно, что наименьшей длинно обладает путь луча, отразившегося в точке О, для которого угол отражения равен углу падения.

Геометрическая оптика 23. 7 Пусть луч распространяется из точки А в точку В. Эти точки находятся в средах с различными показателями преломления. Тогда произвольная оптическая длина между этими точками равна Чтобы найти экстремальное значение, продифференцируем L по х и приравняем полученное выражение нулю: Множители при n 1 n 2 равны соответственно sinα и sinβ. Таким образом, мы приходим к соотношению

Геометрическая оптика 23. 8 Среду с меньшим абсолютным показателем преломления называют оптически менее плотной. При переходе света из оптически более плотной среды в оптически менее плотную n 2 < n 1 (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол αпр, который называется предельным углом полного внутреннего отражения. Для угла падения α = αпр sin β = 1 значение sinαпр = n 2 / n 1 < 1. Если второй средой является воздух (n 2 ≈ 1), то формулу удобно переписать в виде

Геометрическая оптика 23. 9 Для границы раздела стекло–воздух (n = 1, 5) критический угол равен αпр = 42°, для границы вода–воздух (n = 1, 33) – αпр = 48, 7°. Явление полного внутреннего отражения находит применение во многих оптических устройствах. Наиболее интересным и практически важным применением является создание волоконных световодов, которые представляют собой тонкие (от нескольких микрометров до миллиметров) произвольно изогнутые нити из оптически прозрачного материала (стекло, кварц). Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей.

Геометрическая оптика 23. 10 Луч, прошедший через плоскопараллельную пластину погруженную в другое вещество, оказывается параллельным падающему лучу. n 1 n 2 n 1 α β β 1 α 1

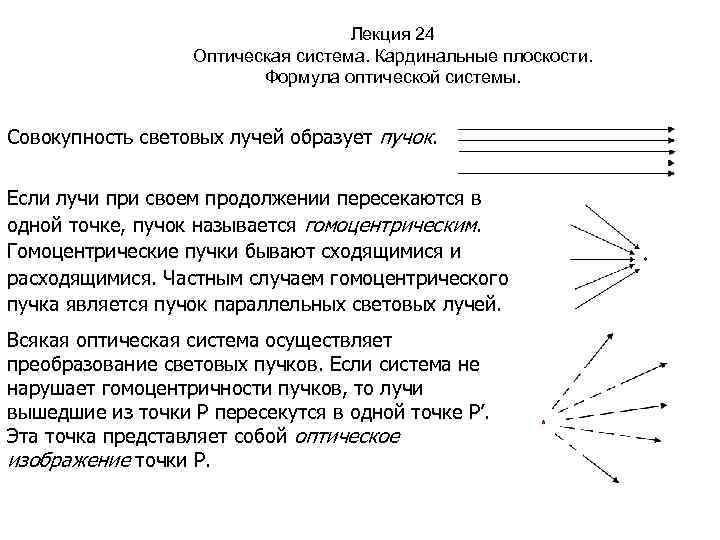Лекция 24 Оптическая система. Кардинальные плоскости. Формула оптической системы. Совокупность световых лучей образует пучок. Если лучи при своем продолжении пересекаются в одной точке, пучок называется гомоцентрическим. Гомоцентрические пучки бывают сходящимися и расходящимися. Частным случаем гомоцентрического пучка является пучок параллельных световых лучей. Всякая оптическая система осуществляет преобразование световых пучков. Если система не нарушает гомоцентричности пучков, то лучи вышедшие из точки Р пересекутся в одной точке Р’. Эта точка представляет собой оптическое изображение точки Р.

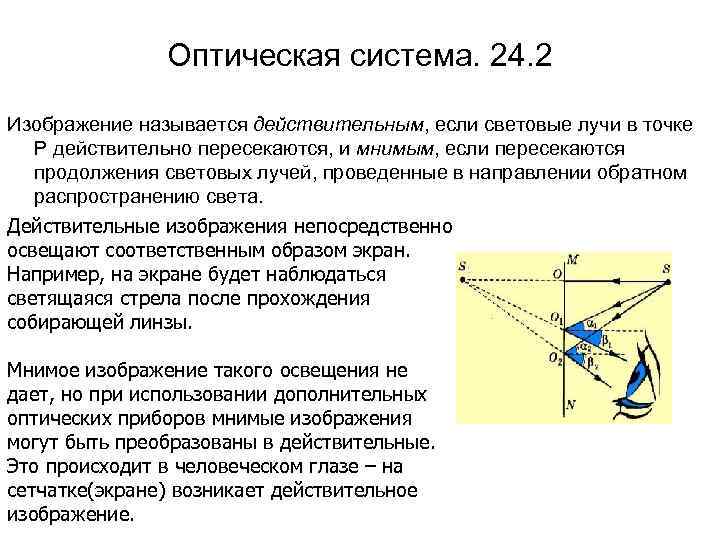Оптическая система. 24. 2 Изображение называется действительным, если световые лучи в точке Р действительно пересекаются, и мнимым, если пересекаются продолжения световых лучей, проведенные в направлении обратном распространению света. Действительные изображения непосредственно освещают соответственным образом экран. Например, на экране будет наблюдаться светящаяся стрела после прохождения собирающей линзы. Мнимое изображение такого освещения не дает, но при использовании дополнительных оптических приборов мнимые изображения могут быть преобразованы в действительные. Это происходит в человеческом глазе – на сетчатке(экране) возникает действительное изображение.

Оптическая система. 24. 3 Вследствие обратимости световых лучей источник света Р и изображение Р’ могут поменяться местами – точечный источник помещенный в точку Р’ будет иметь изображение в точке Р. С помощью оптической системы все бесконечное множество точек Р отображается в виде бесконечного множества точек Р’. Первое бесконечное множество называется пространством предметов, второе – пространством изображений. Оптическая система представляет собой совокупность отражающих и преломляющих поверхностей, отделяющих друг от друга оптически однородные среды. Оптическая система образованная сферическими поверхностями, называется центрированной, если центры всех поверхностей лежат на одной прямой. Эту прямую называют оптической осью системы.

Оптическая система. 24. 4 Пусть на центрированную оптическую систему падает параллельный пучок лучей. Этот пучок можно рассматривать, как вышедший из точечного источника, расположенного на бесконечности т. е. гомоцентрический пучок. Так как система не нарушает гомоцентричности, то по выходе из нее пучок должен остаться гомоцентричным. Следовательно, вышедший из системы пучок должен быть либо сходящимся, либо расходящимся. Точка F’, в которой пересекаются вышедшие из системы лучи, называется задним или вторым фокусом системы. Задний фокус представляет собой точку, сопряженную с точкой удаленной на бесконечность в пространстве предметов и лежащей на оптической оси системы. Бесконечно удаленной плоскости в пространстве предметов перпендикулярной оптической оси будет соответствовать в пространстве изображений плоскость, проходящая через задний фокус и тоже перпендикулярная оптической оси. Эта плоскость называется фокальной.

Оптическая система. 24. 5 В пространстве предметов существует лежащая на оптической оси точка F, обладающая тем свойством, что вышедшие из нее или сходящиеся в ней лучи после прохождения через систему становятся параллельными оптической оси. Эта точка называется передним или первым фокусом системы, а проходящая через нее плоскость перпендикулярная главной оптической оси называется передней фокальной плоскостью. Рассмотрим две произвольные сопряженные плоскости перпендикулярные оптической оси. Отрезок величиной длиной у, лежащей в плоскости в пространстве предметов, будет иметь своим изображением отрезок y’, лежащей в сопряженной плоскости. При этом изображение y’ может быть обращено либо в туже сторону, что и предмет либо в обратную. В первом случае изображение называется прямым, во втором обратным.

Оптическая система. 24. 6 Отрезки, откладываемые от оптической оси вверх, считаются положительными, вниз – отрицательными. Отношение линейных размеров изображения и предмета называется линейным или поперечным увеличением: Линейное увеличение – алгебраическая величина. Оно положительное, если изображение прямое, и отрицательное, если изображение обратное. Оказывается существуют две сопряженные плоскости, которые отображают друга с линейным увеличением β=+1. Такая плоскость расположенная в пространстве предметов называется передней или первой главной плоскостью H, расположенная же в пространстве изображений – задней или второй главной плоскостью Н’. Точки пересечения этих плоскостей с главной оптической осью называются главными точками.

Оптическая система. 24. 7 Также существуют узловые точки или узлы. Сопряженные лучи, проходящие через узлы, параллельны между собой. Перпендикулярные к оптической оси плоскости, проходящие через узлы, называются узловыми плоскостями Фокальные, узловые и главные плоскости называются кардинальными плоскостями оптической системы. Главные точки, фокусы и узлы называются кардинальными точками. Расстояние от передней главной точки до переднего фокуса называется передним фокусным расстоянием f. Аналогично – есть заднее фокусное расстояние f’. Фокусные расстояния – алгебраические величины. Они являются положительными, если фокус находится справа от соответствующей ему главной точки и отрицательными если слева.

Оптическая система. 24. 8 Между фокусными расстояниями центрированной оптической системы, образованной сферическими поверхностями существует следующее соотношение Отсюда следует, что если показатели преломления сред в пространстве предметов и изображений одинаков, то одинаковы по модулю и фокусные расстояния. Величина Называется оптической силой системы. Чем больше оптическая сила, тем сильнее система преломляет световые лучи, и следовательно тем меньше фокусное расстояние. Оптическая сила системы Ф измеряется в СИ в диоптрях Дп.

Оптическая система. 24. 9 Задание кардинальных плоскостей или точек полностью определяет свойства оптической системы. В частности, зная положение кардинальных плоскостей, можно построить оптическое изображение, даваемое системой. Таким образом, должно существовать соотношение, связывающее положение предмета, оптические характеристики системы и положение изображения. Расчеты дают следующее соотношение: x – расстояние от предмета до переднего фокуса, x’ – расстояние от заднего фокуса до изображения. Это соотношение называется формулой Ньютона. Если показатели преломления сред с двух сторон от системы одинаковы то формула Ньютона принимает вид:

Оптическая система. 24. 10 От формулы, связывающей расстояния x и x’, можно перейти к формуле связывающей расстояния от предмета и изображения до главных точек s s’: Если показатели преломления сред с двух сторон от системы одинаковы то это соотношение принимает вид: Также можно получить выражения для линейного увеличения, даваемого центрированной оптической системы:

Лекция 25 Тонкая линза. Формула линзы. Ход лучей в тонких линзах. Построение изображений в собирающей линзе. Построение изображений в рассеивающей линзе. Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой в противном случае линзу называют толстой. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше.

Тонкие линзы. 25. 2 В случае тонкой линзы вершины преломляющих поверхностей можно считать находящимися в одной точке, которую называют оптическим центром линзы. В тонкой линзе обе главные плоскости линзы проходят через ее оптический центр. Если показатели преломления сред, находящихся по обе стороны линзы, одинаковы, то узлы совпадают с главными точками, т. е. помещаются также в оптическом центре линзы. Отсюда вытекает, что любой луч, идущий через оптический центр линзы, не изменяет своего направления. . . Все прямые, проходящие через оптический центр, называются побочными оптическими осями.

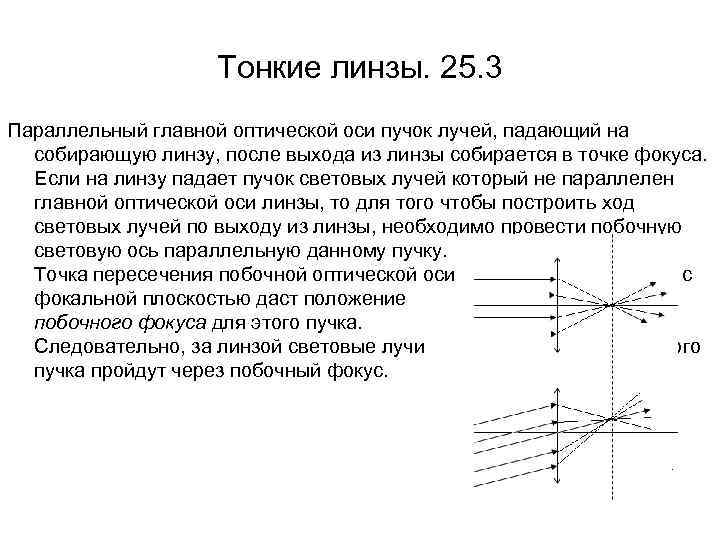Тонкие линзы. 25. 3 Параллельный главной оптической оси пучок лучей, падающий на собирающую линзу, после выхода из линзы собирается в точке фокуса. Если на линзу падает пучок световых лучей который не параллелен главной оптической оси линзы, то для того чтобы построить ход световых лучей по выходу из линзы, необходимо провести побочную световую ось параллельную данному пучку. Точка пересечения побочной оптической оси с фокальной плоскостью даст положение побочного фокуса для этого пучка. Следовательно, за линзой световые лучи этого пучка пройдут через побочный фокус.

Тонкие линзы. 25. 4 Если параллельный главной оптической оси пучок световых лучей падает на рассеивающую линзу, то после выхода он становится расходящимся, так что продолжения лучей собираются в переднем фокусе. Если же на линзу падает пучок лучей не параллельный главной оптической оси, то необходимо провести побочную ось параллельную пучку. Точка пересечения побочной оптической оси даст положение побочного фокуса. Пучок расходится таким образом, что продолжения световых лучей, проведенные против направления распространения, должны дать проходить через побочный фокус. Фокусное расстояние тонкой линзы определяется радиусами сферических поверхностей, образующих линзу, а также показателями преломления линзы и среды в которой находится линза:

Тонкие линзы. 25. 5 Так как главные плоскости проходят через оптический центр тонкой линзы, то f и f’ введенные, как расстояния до главных плоскостей в случае тонких линз в тоже время являются расстояниями от фокуса до тонкой линзы. Как и любая оптическая система, тонкая линза может давать изображения, которые бывают прямыми и обратными, действительными и мнимыми, увеличенными и уменьшенными. Можно получить частный случай формулы оптической системы применительно к тонкой линзе. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде: Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.

Тонкие линзы. 25. 6 Величины d и f также подчиняются определенному правилу знаков: d > 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений; d < 0 и f < 0 – для мнимых источников и изображений. Для построения изображения плоского предмета, опирающегося одним концом на оптическую ось и перпендикулярного ей, необходимо построить изображение того конца предмета, который не опирается на оптическую ось, а затем опустить перпендикуляр на главную оптическую ось. Чтобы построить изображение этой точки необходимо пустить два произвольных луча на линзу, пересечение этих световых лучей после выхода из линзы даст положение изображения. В принципе можно пустить любые лучи, однако проще всего пустить луч параллельный главной оптической оси и луч, проходящий через центр оптической судьбы.

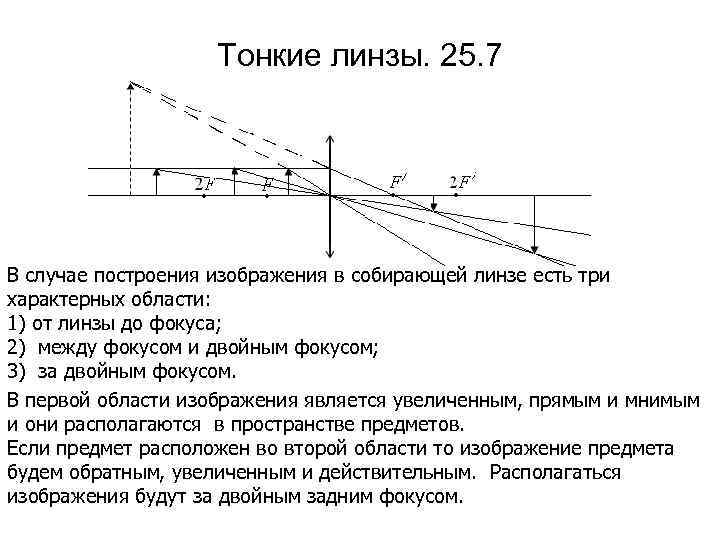Тонкие линзы. 25. 7 В случае построения изображения в собирающей линзе есть три характерных области: 1) от линзы до фокуса; 2) между фокусом и двойным фокусом; 3) за двойным фокусом. В первой области изображения является увеличенным, прямым и мнимым и они располагаются в пространстве предметов. Если предмет расположен во второй области то изображение предмета будем обратным, увеличенным и действительным. Располагаться изображения будут за двойным задним фокусом.

Тонкие линзы. 25. 8 Если предметы будут располагаться за двойным передним фокусом, то изображения будут уменьшенными, обратными и действительными. Располагаться они будут между задним фокусом и двойным задним фокусом. Есть еще две точки на оптической оси которые изображения которых не было описано – двойной фокус и фокус. Изображение предмета расположенного на расстоянии равным двойному фокусному расстоянию будет находиться в двойном заднем фокусе и иметь линейное увеличении -1, т. е. оно будет обратным, действительным его размеры будут такие же, как и предмета. Предмет расположенный в фокальной плоскости будет иметь изображение на бесконечности, так как лучи вышедшие из любой точки в фокальной плоскости после прохождения тонкой линзы превращаются в параллельный пучок.

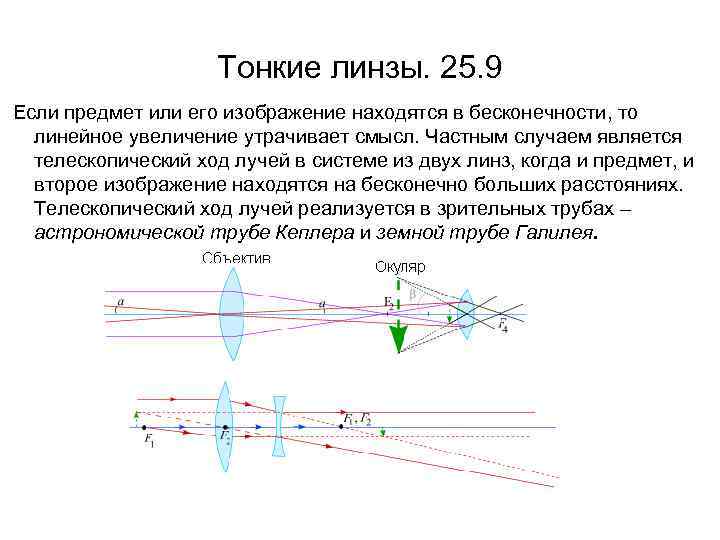Тонкие линзы. 25. 9 Если предмет или его изображение находятся в бесконечности, то линейное увеличение утрачивает смысл. Частным случаем является телескопический ход лучей в системе из двух линз, когда и предмет, и второе изображение находятся на бесконечно больших расстояниях. Телескопический ход лучей реализуется в зрительных трубах – астрономической трубе Кеплера и земной трубе Галилея.

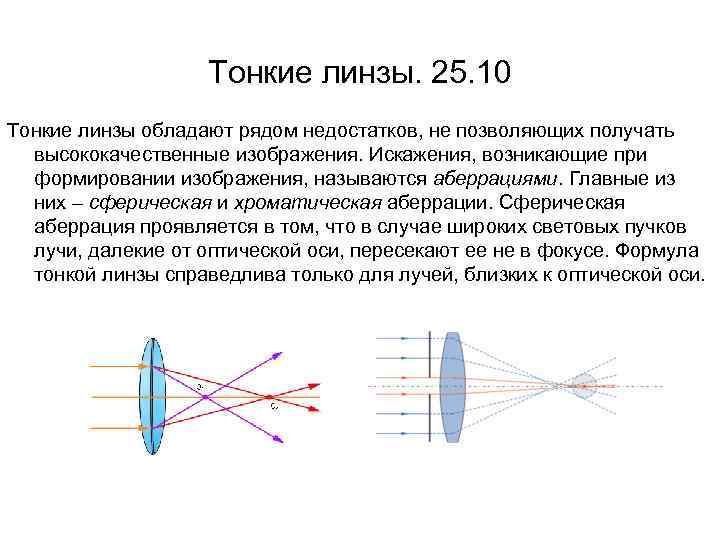Тонкие линзы. 25. 10 Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями. Главные из них – сферическая и хроматическая аберрации. Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси.

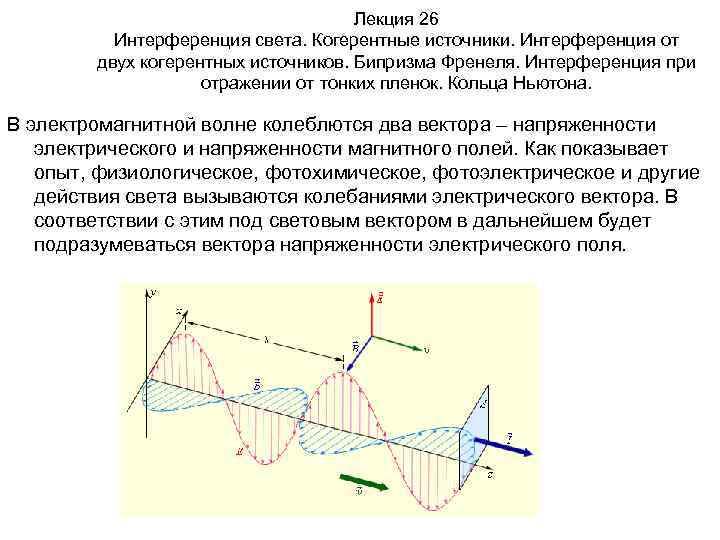Лекция 26 Интерференция света. Когерентные источники. Интерференция от двух когерентных источников. Бипризма Френеля. Интерференция при отражении от тонких пленок. Кольца Ньютона. В электромагнитной волне колеблются два вектора – напряженности электрического и напряженности магнитного полей. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрического вектора. В соответствии с этим под световым вектором в дальнейшем будет подразумеваться вектора напряженности электрического поля.

Интерференция. 26. 2 Пусть в некоторую точку пространства приходят две световые волны. Эти волны возбуждают в пространстве колебания одинакового направления. Амплитуда суммарного колебания определяется по правилу сложения двух колебаний одинакового направления. В результате получим: Если разность фаз δφ=(α 1 -α 2) возбуждаемых волнами колебаний остается постоянной во времени. То волны называются когерентными. В случае говорят о сложении колебаний в фазе или синфазном сложении, для которого следует, что амплитуда суммарных колебаний равна сумме амплитуд каждого из колебаний

Интерференция. 26. 3 В случае говорят о сложении колебаний с противоположными фазами или противофазном сложении, для которого следует, что амплитуда суммарных колебаний равна модулю разности амплитуд каждого из колебаний: Квадрат амплитуды напряженности электрического поля пропорционален интенсивности I электромагнитного поля. С учётом этого следует выражение для интенсивности суммы колебаний электромагнитных волн : Явление перераспределения в пространстве интенсивности электромагнитного поля, представляющего собой сумму двух монохроматических волн одной частоты, в зависимости от их разности фаз называется интерференцией.

Интерференция. 26. 4 Явление интерференции можно наблюдать, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. В результате получим две когерентные волны. Затем необходимо сложить их, предварительно заставив пройти различные оптические пути. В общем случае полученные таким образом две световые волны пройдут до точки сложения пути s 1 и s 2. Первая волна возбудит в точке сложения колебание А вторая волна – колебание

Интерференция. 26. 5 скорость распространения первой и второй волны Таким образом, разность фаз колебаний, возбуждаемых в точке сложения, будет равна оптическая разность хода

Интерференция. 26. 6 Таким образом, получаем, что если оптическая разность хода равна целому числу длин волн, то волны в точке сложения колеблются синфазно, так, как разность фаз равна числу кратному 2π. Т. е. получаем условие интерференционного максимума: Если же оптическая разность хода равна полуцелому числу длин волн в вакууме то волны в точке сложения колеблются в противофазе, так, как разность фаз равна Т. е. получаем условие интерференционного минимума: Рассмотрим более подробно основные свойства интерференционной картины, создаваемой двумя источниками электромагнитных волн одинаковой интенсивности и наблюдаемой на плоском экране, расположенным на расстоянии l от плоскости расположения от источников.

Интерференция. 26. 7 В качестве таких источников могут быть, например две бесконечноузкие, параллельные друг - другу щели или два отверстия бесконечно малого диаметра, расстояние между которыми d<

Интерференция. 26. 8 Ширина интерференционной полосы опредемая, как расстояние между соседними интерференционными максимумами или минимумами, интерференционные порядки которых отличаются на единицу.

Интерференция. 26. 9 Бизеркала Френеля – два плоских зеркала располагаются так, что их отражающие поверхности образуют угол близкий к π ширина интерференционной полосы - область перекрытия волн на экране число интерференционных полос

Интерференция. 26. 10 Одним из наиболее часто используемых в лабораториях приборов для получения интерференции является бипризма Френеля - изготовленные из одного куска стекла две призмы с малым преломляющим углом θ имеющие общее основание. При освещении бипризмы Френеля монохроматическим светом от источника, расположенного на расстоянии а на экране будет наблюдаться картина чередующихся светлых и темных ширина интерференционной полосы число интерференционных полос

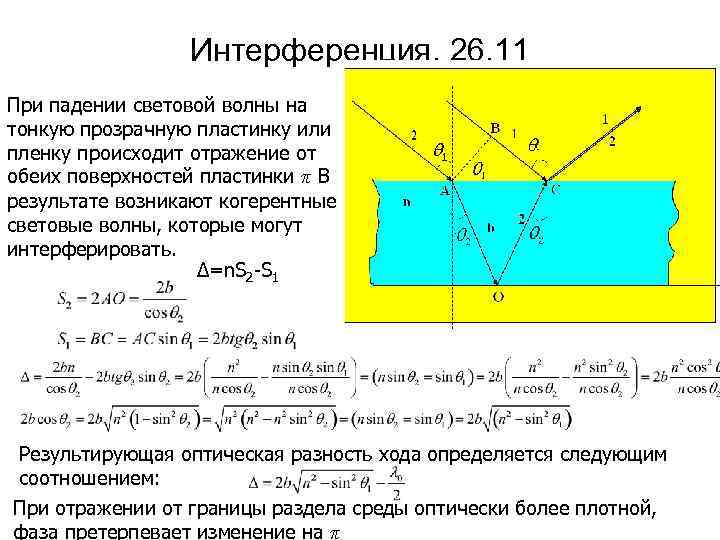Интерференция. 26. 11 При падении световой волны на тонкую прозрачную пластинку или пленку происходит отражение от обеих поверхностей пластинки π В результате возникают когерентные световые волны, которые могут интерферировать. Δ=n. S 2 -S 1 Результирующая оптическая разность хода определяется следующим соотношением: При отражении от границы раздела среды оптически более плотной, фаза претерпевает изменение на π

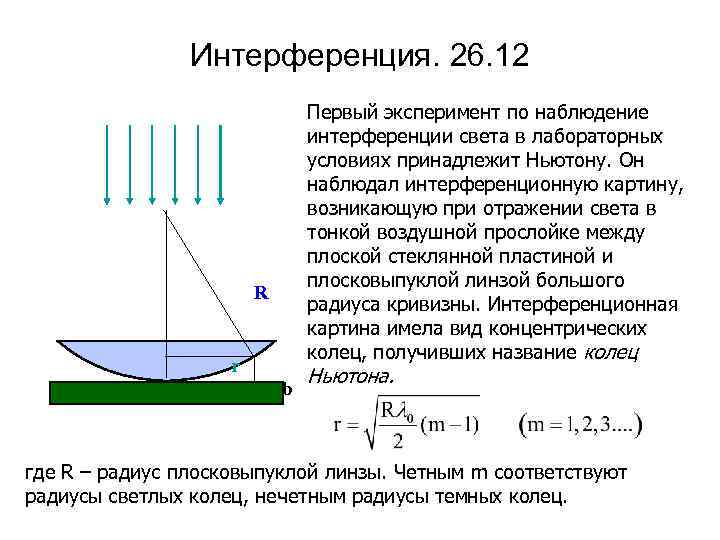Интерференция. 26. 12 Первый эксперимент по наблюдение интерференции света в лабораторных условиях принадлежит Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Интерференционная картина имела вид концентрических колец, получивших название колец R r b Ньютона. где R – радиус плосковыпуклой линзы. Четным m соответствуют радиусы светлых колец, нечетным радиусы темных колец.

Лекция 27 Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля. Диаграмма Френеля. Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым. Т. Юнгом. Независимо от него французский ученый О. Френель развил количественную теорию дифракционных явлений (1818 г. ).

Дифракция. 27. 2 В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент времен. Принцип Гюйгенса Различают два вида явления дифракции в зависимости от расстояния точки наблюдения до препятствия или неоднородности, а также от вида волнового фронта в точке наблюдения. Если точка наблюдения расположена достаточно далеко от препятствия и в точку наблюдения после взаимодействия с неоднородностью приходит плоская волна, то говорят о дифракции Фраунгофера. В остальных случаях говорят о дифракции Френеля.

Дифракция. 27. 3 • Как следует из принципа Гюйгенса- Френеля амплитуда волны в точке наблюдения Р, создаваемая источником монохроматической электромагнитной волны в точке О, может быть найдена как суперпозиция амплитуд сферических волн, испускаемых вторичными источниками на произвольной замкнутой поверхности S, охватывающей точку O. Пусть S сферическая поверхность радиуса a c центром в точке S. Разобьем волновую поверхность на кольцевые зоны, зоны Френеля, таким образом, что бы расстояние от краев каждой зоны до точки Р отличались на Тогда расстояние от внешнего края m-й зоны до точки Р можно представить следующим образом:

Дифракция. 27. 4 Колебания приходящие в точку Р от аналогичных точек двух соседних зон, находятся в противофазе. Поэтому и результирующее колебания, создаваемые каждой из зон в целом будут для соседних зон различаться по фазе на π. Для определения результирующей амплитуды в точке Р, необходимо знать амплитуду создаваемую каждой из зон. Очевидно, что амплитуда каждой из зон зависит от ее площади. Определим площадь произвольной зоны Френеля. Эта площадь будет являться разностью площадей двух сферических сегментов, ганицы которых соответствуют m-ой и (m-1)-ой зонам Френеля.

Дифракция. 27. 5 Площадь сферического сегмента вычисляется по формуле где hm – высота сегмента. Определим ее S b a т. к. , то Р O Таким образом, получаем площадь сферического сегмента: экран

Дифракция. 27. 6 В результате площадь m-й зоны Френеля Полученное выражение не зависит от m. Следовательно, при не слишком больших m площади зон Френеля примерно одинаковы. Радиус m-ой зоны Френеля: Если положить a=b=1 м и λ=0. 5 мкм, то для радиуса первой зоны получается значение 0. 5 мм.

Дифракция. 27. 7 Одинаковые по площади зоны должны были бы возбуждать в точке наблюдения колебания с одинаковой амплитудой. Однако у каждой последующей зоны угол α между лучом, проведенным в точку наблюдения, и нормалью к волновой поверхности возрастает. Френель высказал предположение (подтвержденное экспериментом), что с увеличением угла α амплитуда колебаний уменьшается, хотя и незначительно A 1 > A 2 > A 3 >. . . > Am, С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.

Дифракция. 27. 8 Так как расстояния от двух соседних зон до точки наблюдения отличаются на λ / 2, следовательно, возбуждаемые этими зонами колебания находится в противофазе. Поэтому волны от любых двух соседних зон почти гасят друга. Суммарная амплитуда в точке наблюдения есть A = A 1 – A 2 + A 3 – A 4 +. . . = A 1 – (A 2 – A 3) – (A 4 – A 5) –. . . Таким образом, суммарная амплитуда колебаний в точке P всегда меньше амплитуды колебаний, которые вызвала бы одна первая зона Френеля. В частности, если бы были открыты все зоны Френеля, то до точки наблюдения дошла бы невозмущенная препятствием волна с амплитудой A 0. В этом случае можно записать: так как выражения, стоящие в скобках, равны нулю. Следовательно, действие (амплитуда), вызванное всем волновым фронтом, равно половине действия одной первой зоны.

Дифракция. 27. 9 Если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастает. Например, если открыты 1, 3 и 5 зоны, то

Дифракция. 27. 10 Разобьем волновую поверхность на кольцевые зоны, аналогичные зонам Френеля, но гораздо меньше по ширине ( разность хода от краев зоны до точки Р составляет одинаковую для всех зон малую долю λ). Колебание, создаваемое в точке Р каждой из зон, изобразим в виде вектора, длина которого равна амплитуде колебания, а угол, образуемый вектором с направлением принятым за начало отсчета, дает начальную фазу колебания. В силу разбиения зон два любых соседних вектора будут повернуты друг относительно друга на один угол. Также амплитуда при переходе от зоны к зоне уменьшается. Следовательно, векторная диаграмма, получаемая при сложении колебаний возбуждаемых отдельными зонами, будет иметь вид спирали.

Лекция 28 Дифракция Френеля от простейших преград. Дифракция от круглого отверстия. Дифракция Френеля от простейших преград. Дифракция от непрозрачного круглого диска. Дифракционная решетка. Метод расчёта с помощью зон Френеля интенсивности света в точке наблюдения применим для анализа задач дифракции электромагнитных волн на простых по форме препятствиях. Пусть экран с отверстием радиуса r 0 расположен так, так что центр отверстия расположен на прямой, перпендикулярной плоскости экрана с отверстием, соединяющей точку наблюдения P и точку источника S. Разобьем поверхность волнового фронта, падающего на отверстие, на зоны Френеля по отношению к точке наблюдения P. Будем называть открытыми такие зоны Френеля, которые располагаются внутри отверстия. Соответственно зоны Френеля, попадающие на поверхность непрозрачного экрана, называются закрытыми.

Дифракция. 28. 2 Если размер отверстия во много раз меньше расстояний от экрана до источника a и от экрана до точки наблюдения b, то можно найти число m открытых отверстием зон Френеля:

Дифракция. 28. 3 Суммарная амплитуда в точке наблюдения есть A = A 1 – A 2 + A 3 – A 4 +. . . ±Am = 0. 5(A 1±Am) Амплитуды волн зон Френеля при их небольшом числе можно считать примерно одинаковыми. По этой причине в точке Р будет либо максимум, либо минимум интенсивности дифрагированной волны от отверстия в зависимости соответственно от нечётности или чётности числа открытых зон Френеля.

Дифракция. 28. 4 m – четное Рассмотрим наблюдение интенсивности дифрагированного отверстием света на непрозрачном экране, помещённом в точку P, параллельно плоскости экрана с отверстием. В виду симметрии наблюдаемое на экране распределение интенсивности света будет иметь характер чередующихся тёмных и светлых колец с центром в точке P. Интенсивность света в максимумах по мере удаления от центральной точки будет убывать. Убывание объясняется тем, что при смещении точки наблюдения P из центра на периферию открытые из точки P центральные зоны Френеля частично закрываются и, кроме того, частично открываются новые зоны Френеля, ослабляющие интенсивность света в точке наблюдения. m – нечетное

Дифракция. 28. 5 Пусть свет из точки источника S освещает непрозрачный диск радиуса r 0, за которым на прямой, перпендикулярной плоскости диска и проведенной через его центр, располагается точка наблюдения P. Как и выше, будем считать, что размер диска во много раз меньше расстояний от диска до источника a и от диска до точки наблюдения b.

Дифракция. 28. 6 Предположим, что диск из точки наблюдения P закрывает m зон Френеля. Тогда амплитуда света A в точке наблюдения будет равна алгебраической сумме амплитуд волн открытых зон Френеля: Учитывая, что амплитуды соседних зон Френеля примерно равны другу, однотипные выражение в скобках можно положить равными нулю, и тогда получим: Отсюда следует, что в центре дифракционной картины, создаваемой диском, всегда наблюдается светлое пятно, независимо от размеров диска.

Дифракция. 28. 7 Дифракционная картина от диска, наблюдаемая на экране, имеет характер чередующихся тёмных и светлых колец, в центре которых находится светлое пятно. Структура дифракционной картины света от непрозрачного диска имеет общие черты с дифракционной картиной света от отверстия того же диаметра в непрозрачном экране. Периодическая система одинаковых, расположенных на одном и том же расстоянии друг от друга щелей, называется дифракционной решёткой. Расстояние d между серединами соседних щелей называется периодом дифракционной решётки. Обычно в дифракционных решётках, используемых в оптике, щели являются узкими, т. е. их размер b во много раз меньше периода дифракционной решётки d<

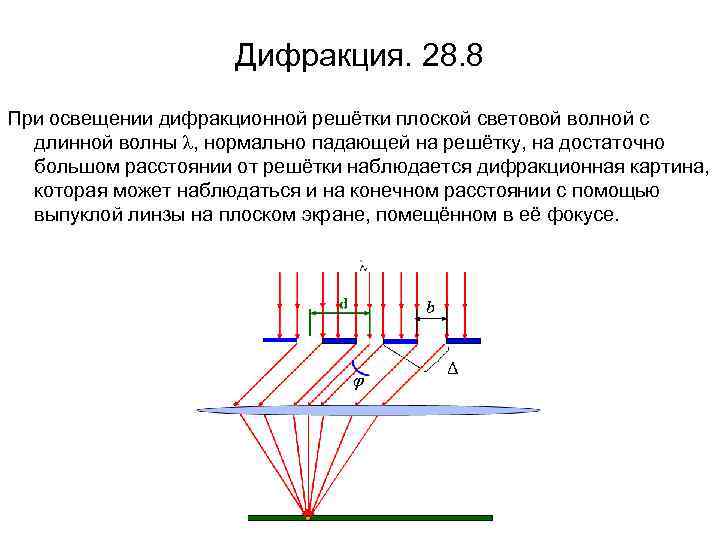Дифракция. 28. 8 При освещении дифракционной решётки плоской световой волной с длинной волны λ, нормально падающей на решётку, на достаточно большом расстоянии от решётки наблюдается дифракционная картина, которая может наблюдаться и на конечном расстоянии с помощью выпуклой линзы на плоском экране, помещённом в её фокусе.

Дифракция. 28. 9 Характер распределения интенсивности представляет собой чередование главных дифракционных максимумов, между которыми располагаются побочные дифракционные максимумы и минимумы. Главные дифракционные максимумы интенсивности располагаются в направлениях φm, в которых волны от щелей в точке наблюдения имеют разность хода, кратную λ, т. е. : где - целые числа. Главный дифракционный максимум, соответствующий направлению, называется дифракционным максимумом m- го порядка. Центральный дифракционный максимум соответственно является дифракционным максимумом нулевого порядка (m=0) и имеет наибольшую величину.

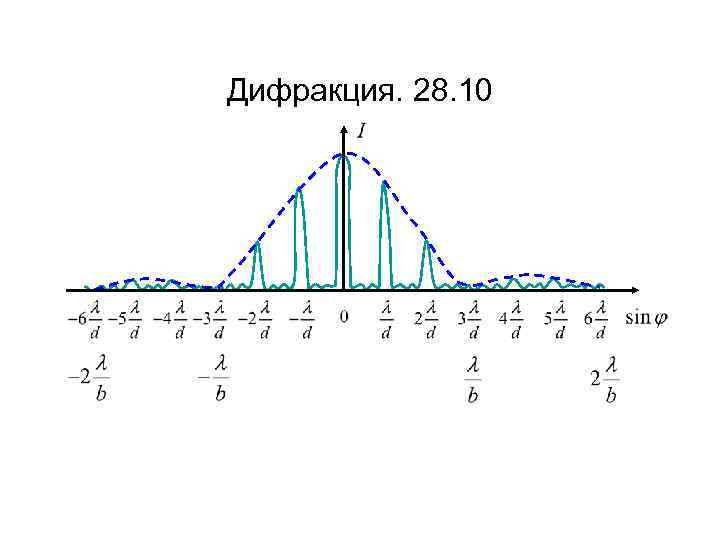Дифракция. 28. 10