Лекція 1 ВСТУП ДО ТЕОРІЇ РОЗПОДІЛУ ІНФОРМАЦІЇ




































Лекция_ОТРИ+.ppt
- Количество слайдов: 45
 Лекція 1 ВСТУП ДО ТЕОРІЇ РОЗПОДІЛУ ІНФОРМАЦІЇ
Лекція 1 ВСТУП ДО ТЕОРІЇ РОЗПОДІЛУ ІНФОРМАЦІЇ
 ЛІТЕРАТУРА • 1. Лившиц Б. С. , Пшеничников А. П. , Харкевич А. Д. Теория телетрафика. –М. : Связь, 1979. – 224 с. • 2. Омельченко А. В. Основи аналізу систем розподілу інформації. Навч. посібник. – Харків: ХНУРЕ, 2008. – 136 с. • 3. Безрук В. М. , Бідний Ю. М. , Омельченко А. В. Інформаційні мережі зв'язку. Ч. 1. Математичні основи інформаційних мереж зв'язку. – Харків: ХНУРЕ, 2011. – 292 с. • 4. Крылов В. В. , Самохвалова С. С. Теория телетрафика и ее приложения. – СПб. : BHV-Санкт- Петербург, 2005. – 288 с. 5. Саати Т. Элементы теории массового обслуживания и ее приложения. – М. : Сов. радио, 1965. – 510 с. 6. Клейнрок Л. Теория массового обслуживания. – М. : Машиностроение, 1979 – 432 с.
ЛІТЕРАТУРА • 1. Лившиц Б. С. , Пшеничников А. П. , Харкевич А. Д. Теория телетрафика. –М. : Связь, 1979. – 224 с. • 2. Омельченко А. В. Основи аналізу систем розподілу інформації. Навч. посібник. – Харків: ХНУРЕ, 2008. – 136 с. • 3. Безрук В. М. , Бідний Ю. М. , Омельченко А. В. Інформаційні мережі зв'язку. Ч. 1. Математичні основи інформаційних мереж зв'язку. – Харків: ХНУРЕ, 2011. – 292 с. • 4. Крылов В. В. , Самохвалова С. С. Теория телетрафика и ее приложения. – СПб. : BHV-Санкт- Петербург, 2005. – 288 с. 5. Саати Т. Элементы теории массового обслуживания и ее приложения. – М. : Сов. радио, 1965. – 510 с. 6. Клейнрок Л. Теория массового обслуживания. – М. : Машиностроение, 1979 – 432 с.
 ЛІТЕРАТУРА • 7. Шнепс М. А. Системы распределения информации. Методы расчета: Справ. пособие. – М. : Связь, 1979. – 344 с. • 8. Клейнрок Л. Вычислительные системы с очередями. – М. : Мир, 1979 – 600 с. • 9. Уолдренд Дж. Телекоммуникационные и компьютерные сети. Вводный курс. – М. : Постмаркет, 2001. – 480 с. • 10. Методичні вказівки до лабораторних робіт з курсу "Основи теорії масового обслуговування" для студентів усіх форм навчання спеціальностей напрямку “Телекомунікації” /Упоряд. : Ю. М. Бідний, А. В. Омельченко. Харків, ХТУРЕ, 1998. -44 с. • 11. Методичні вказівки до лабораторних робіт з курсу "Системи комутації в електрозв’язку" для студентів усіх форм навчання спеціальностей напрямку “Телекомунікації” /Упоряд. : А. В. Омельченко та ін. , Харків, ХНУРЕ, 2006. - 99 с. • 12. Методичні вказівки до практичних занять з дисципліни "Основи теорії масового обслуговування" для студентів усіх форм навчання спеціальностей напрямку “Телекомунікації” /Упоряд. : С. В. Омельченко, А. В. Омельченко. Харків, ХНУРЕ, 2010. -40 с.
ЛІТЕРАТУРА • 7. Шнепс М. А. Системы распределения информации. Методы расчета: Справ. пособие. – М. : Связь, 1979. – 344 с. • 8. Клейнрок Л. Вычислительные системы с очередями. – М. : Мир, 1979 – 600 с. • 9. Уолдренд Дж. Телекоммуникационные и компьютерные сети. Вводный курс. – М. : Постмаркет, 2001. – 480 с. • 10. Методичні вказівки до лабораторних робіт з курсу "Основи теорії масового обслуговування" для студентів усіх форм навчання спеціальностей напрямку “Телекомунікації” /Упоряд. : Ю. М. Бідний, А. В. Омельченко. Харків, ХТУРЕ, 1998. -44 с. • 11. Методичні вказівки до лабораторних робіт з курсу "Системи комутації в електрозв’язку" для студентів усіх форм навчання спеціальностей напрямку “Телекомунікації” /Упоряд. : А. В. Омельченко та ін. , Харків, ХНУРЕ, 2006. - 99 с. • 12. Методичні вказівки до практичних занять з дисципліни "Основи теорії масового обслуговування" для студентів усіх форм навчання спеціальностей напрямку “Телекомунікації” /Упоряд. : С. В. Омельченко, А. В. Омельченко. Харків, ХНУРЕ, 2010. -40 с.
 Основні питання • Моделі і задачі теорії розподілу інформації • Основні елементи математичних моделей систем розподілу інформації • Класифікація моделей Кендала-Башаріна • Основні задачі теорії розподілу інформації
Основні питання • Моделі і задачі теорії розподілу інформації • Основні елементи математичних моделей систем розподілу інформації • Класифікація моделей Кендала-Башаріна • Основні задачі теорії розподілу інформації
 ЗАДАЧІ ТЕОРІЇ ТЕЛЕТРАФІКУ • Теорія розподілу інформації називається ще теорією телетрафіку. При буквальному перекладі з грецької “теле” означає далеко, а “ трафік “ ( traveho ) – перевезти, переслати. Поняття “телетрафік “ може означати будь-які потоки інформації в СРІ. • Основи нової теорії були закладені у працях датського математика, співробітника Копенгагенської телефонної компанії А. К. Ерланга. Сформульований ним принцип статистичної рівноваги й отримані на його основі формули для розрахунку комутаційних схем і сьогодні є базовими в теорії розподілу інформації та теорії масового обслуговування. В подальшому теорія розподілу інформації розвивалася в роботах багатьох вітчизняних і зарубіжних учених.
ЗАДАЧІ ТЕОРІЇ ТЕЛЕТРАФІКУ • Теорія розподілу інформації називається ще теорією телетрафіку. При буквальному перекладі з грецької “теле” означає далеко, а “ трафік “ ( traveho ) – перевезти, переслати. Поняття “телетрафік “ може означати будь-які потоки інформації в СРІ. • Основи нової теорії були закладені у працях датського математика, співробітника Копенгагенської телефонної компанії А. К. Ерланга. Сформульований ним принцип статистичної рівноваги й отримані на його основі формули для розрахунку комутаційних схем і сьогодні є базовими в теорії розподілу інформації та теорії масового обслуговування. В подальшому теорія розподілу інформації розвивалася в роботах багатьох вітчизняних і зарубіжних учених.
 • Ангер Краруп Ерланг народився в 1878 р. Місті Лонборге в Данії Він був піонером у вивченні трафіку телекомунікаційних систем. У 1909 р. він опублікував свою першу роботу “Теорія вірогідності і телефонія”. Ця робота була визнана у всьому світі, а його формула до цих пір використовується при розрахунках сучасних телекомунікаційних систем. У сорокових роках Agner Krarup Erlang минулого століття в його честь (1878 -1929) була названа одиниця вимірювання трафіку в телекомунікаційних системах.
• Ангер Краруп Ерланг народився в 1878 р. Місті Лонборге в Данії Він був піонером у вивченні трафіку телекомунікаційних систем. У 1909 р. він опублікував свою першу роботу “Теорія вірогідності і телефонія”. Ця робота була визнана у всьому світі, а його формула до цих пір використовується при розрахунках сучасних телекомунікаційних систем. У сорокових роках Agner Krarup Erlang минулого століття в його честь (1878 -1929) була названа одиниця вимірювання трафіку в телекомунікаційних системах.
 • Теорія розподілу інформації являє собою дисципліну, що розробляє методи аналізу й синтезу систем комутації, інформаційних і комп'ютерних систем, а також систем керування. Теорія розподілу інформації ( телетрафіку ) є галуззю теорії масового обслуговування, що в свою чергу є розділом прикладної математики, і вивчає кількісні характеристики процесів масового обслуговування. Нині теорія масового обслуговування, крім інфокомунікацій , ефективно використовується для розв’язання задач торгівлі, транспорту та інших сфер економічної діяльності. • Основними задачами теорії розподілу інформації є задача аналізу СРІ і задача синтезу СРІ. При цьому найбільш суттєві результати досягнуті в області аналізу СРІ.
• Теорія розподілу інформації являє собою дисципліну, що розробляє методи аналізу й синтезу систем комутації, інформаційних і комп'ютерних систем, а також систем керування. Теорія розподілу інформації ( телетрафіку ) є галуззю теорії масового обслуговування, що в свою чергу є розділом прикладної математики, і вивчає кількісні характеристики процесів масового обслуговування. Нині теорія масового обслуговування, крім інфокомунікацій , ефективно використовується для розв’язання задач торгівлі, транспорту та інших сфер економічної діяльності. • Основними задачами теорії розподілу інформації є задача аналізу СРІ і задача синтезу СРІ. При цьому найбільш суттєві результати досягнуті в області аналізу СРІ.
 Основні елементи математичних моделей систем розподілу інформації • Теорія розподілу інформації вивчає кількісні характеристики функціонування СРІ в рамках математичних моделей [1, 2]. • Математична модель СРІ включає такі основні елементи: 1) потік викликів; 2) структуру СРІ; 3) дисципліну обслуговування викликів; 4) сукупність характеристик якості обслуговування викликів. • Потоком викликів називається послідовність викликів, що надходять на СРІ у деякі моменти часу. Під викликом розуміється заявка на обслуговування. • Структура СРІ визначається складом приладів (каналів) системи і взаємозв'язками між ними. • Системи розподілу інформації можуть мати такі структури: 1) одноканальні або багатоканальні; 2) повнодоступні та не повнодоступні; 3) одноланкові й багатоланкові.
Основні елементи математичних моделей систем розподілу інформації • Теорія розподілу інформації вивчає кількісні характеристики функціонування СРІ в рамках математичних моделей [1, 2]. • Математична модель СРІ включає такі основні елементи: 1) потік викликів; 2) структуру СРІ; 3) дисципліну обслуговування викликів; 4) сукупність характеристик якості обслуговування викликів. • Потоком викликів називається послідовність викликів, що надходять на СРІ у деякі моменти часу. Під викликом розуміється заявка на обслуговування. • Структура СРІ визначається складом приладів (каналів) системи і взаємозв'язками між ними. • Системи розподілу інформації можуть мати такі структури: 1) одноканальні або багатоканальні; 2) повнодоступні та не повнодоступні; 3) одноланкові й багатоланкові.
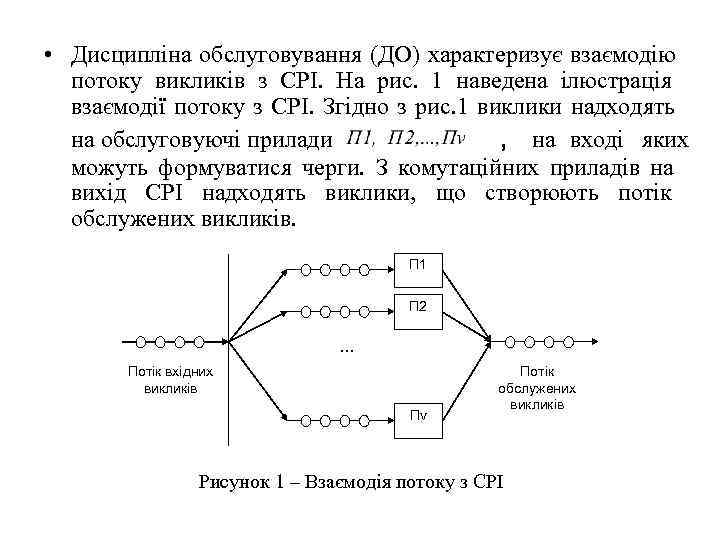
 • Дисципліна обслуговування (ДО) характеризує взаємодію потоку викликів з СРІ. На рис. 1 наведена ілюстрація взаємодії потоку з СРІ. Згідно з рис. 1 виклики надходять на обслуговуючі прилади , на вході яких можуть формуватися черги. З комутаційних приладів на вихід СРІ надходять виклики, що створюють потік обслужених викликів. П 1 П 2 . . . Потік вхідних Потік викликів обслужених викликів Пv Рисунок 1 – Взаємодія потоку з СРІ
• Дисципліна обслуговування (ДО) характеризує взаємодію потоку викликів з СРІ. На рис. 1 наведена ілюстрація взаємодії потоку з СРІ. Згідно з рис. 1 виклики надходять на обслуговуючі прилади , на вході яких можуть формуватися черги. З комутаційних приладів на вихід СРІ надходять виклики, що створюють потік обслужених викликів. П 1 П 2 . . . Потік вхідних Потік викликів обслужених викликів Пv Рисунок 1 – Взаємодія потоку з СРІ
 • Дисципліна обслуговування описується такими основними характеристиками: • 1) способами обслуговування: • а) із втратами, коли не обслужені виклики втрачаються; • б) з очікуванням; • в) з повторними викликами; • г) комбіновані; • 2) законами розподілу тривалості обслуговування викликів: • а) фіксована тривалість; • б) випадкова тривалість із заданим імовірнісним законом; • в) довільний закон розподілу тривалості обслуговування;
• Дисципліна обслуговування описується такими основними характеристиками: • 1) способами обслуговування: • а) із втратами, коли не обслужені виклики втрачаються; • б) з очікуванням; • в) з повторними викликами; • г) комбіновані; • 2) законами розподілу тривалості обслуговування викликів: • а) фіксована тривалість; • б) випадкова тривалість із заданим імовірнісним законом; • в) довільний закон розподілу тривалості обслуговування;
 • 3) режимами пошуку вільних приладів системи (виходів): а) вільний пошук; б) груповий пошук в) індивідуальний пошук; • 4) порядком обслуговування викликів: а) у порядку черги; б) у випадковому порядку; в) обслуговування пакетами; • 5) наявністю обмежень при обслуговуванні всіх або деяких категорій викликів: а) за тривалістю очікування; б) за тривалістю обслуговування; в) наявністю пріоритетів (переваг) в обслуговуванні викликів певних категорій. • Під якістю обслуговування розуміється, наскільки вчасно і повно проведено обслуговування викликів (вимог, заявок), що надійшли до системи.
• 3) режимами пошуку вільних приладів системи (виходів): а) вільний пошук; б) груповий пошук в) індивідуальний пошук; • 4) порядком обслуговування викликів: а) у порядку черги; б) у випадковому порядку; в) обслуговування пакетами; • 5) наявністю обмежень при обслуговуванні всіх або деяких категорій викликів: а) за тривалістю очікування; б) за тривалістю обслуговування; в) наявністю пріоритетів (переваг) в обслуговуванні викликів певних категорій. • Під якістю обслуговування розуміється, наскільки вчасно і повно проведено обслуговування викликів (вимог, заявок), що надійшли до системи.
 Класифікація моделей Кендала-Башаріна • Існують різні моделі СРІ. Для них були розроблені різні принципи класифікації. Понад п'ятдесят років тому була запропонована класифікація Кендала , що базувалася на використанні лише трьох символів. Для опису складних процесів функціонування сучасних інфокомунікаційних систем ця класифікація була доповнена. Ряд доповнень до класифікації Кендала був розроблений відомим російським ученим в області теорії масового обслуговування Г. П. Башаріним. У сучасній технічній літературі для опису складних СМО тепер використовується класифікація Кендала- Башаріна, що використовує до шести символів. • Згідно з Кендалом-Башаріним , математична модель характеризується послідовністю символів, розділених рискою: X 1/X 2/X 3/X 4/X 5/X 6.
Класифікація моделей Кендала-Башаріна • Існують різні моделі СРІ. Для них були розроблені різні принципи класифікації. Понад п'ятдесят років тому була запропонована класифікація Кендала , що базувалася на використанні лише трьох символів. Для опису складних процесів функціонування сучасних інфокомунікаційних систем ця класифікація була доповнена. Ряд доповнень до класифікації Кендала був розроблений відомим російським ученим в області теорії масового обслуговування Г. П. Башаріним. У сучасній технічній літературі для опису складних СМО тепер використовується класифікація Кендала- Башаріна, що використовує до шести символів. • Згідно з Кендалом-Башаріним , математична модель характеризується послідовністю символів, розділених рискою: X 1/X 2/X 3/X 4/X 5/X 6.
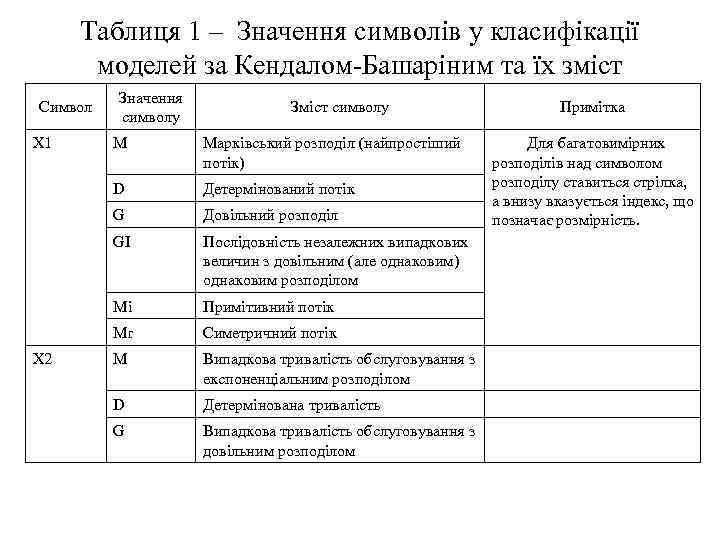
 • Тут перший символ X 1 позначає розподіл інтервалів між викликами й характеризує потік; другий X 2 – розподіл тривалості обслуговування; третій X 3 – структуру системи розподілу інформації; четвертий X 4 – спосіб обслуговування викликів; п'ятий X 5 – дисципліну черги; шостий X 6 – порядок заняття вільних приладів. Таким чином, символи X 2, Х 4, X 5 і X 6 характеризують дисципліну обслуговування. • Значення символів X 1 – X 6 та їх зміст вказані в табл. 1.
• Тут перший символ X 1 позначає розподіл інтервалів між викликами й характеризує потік; другий X 2 – розподіл тривалості обслуговування; третій X 3 – структуру системи розподілу інформації; четвертий X 4 – спосіб обслуговування викликів; п'ятий X 5 – дисципліну черги; шостий X 6 – порядок заняття вільних приладів. Таким чином, символи X 2, Х 4, X 5 і X 6 характеризують дисципліну обслуговування. • Значення символів X 1 – X 6 та їх зміст вказані в табл. 1.
 Таблиця 1 – Значення символів у класифікації моделей за Кендалом-Башаріним та їх зміст Значення Символ Зміст символу Примітка символу X 1 M Марківський розподіл (найпростіший Для багатовимірних потік) розподілів над символом D Детермінований потік розподілу ставиться стрілка, а внизу вказується індекс, що G Довільний розподіл позначає розмірність. GI Послідовність незалежних випадкових величин з довільним (але однаковим) однаковим розподілом Mi Примітивний потік Mr Симетричний потік X 2 M Випадкова тривалість обслуговування з експоненціальним розподілом D Детермінована тривалість G Випадкова тривалість обслуговування з довільним розподілом
Таблиця 1 – Значення символів у класифікації моделей за Кендалом-Башаріним та їх зміст Значення Символ Зміст символу Примітка символу X 1 M Марківський розподіл (найпростіший Для багатовимірних потік) розподілів над символом D Детермінований потік розподілу ставиться стрілка, а внизу вказується індекс, що G Довільний розподіл позначає розмірність. GI Послідовність незалежних випадкових величин з довільним (але однаковим) однаковим розподілом Mi Примітивний потік Mr Симетричний потік X 2 M Випадкова тривалість обслуговування з експоненціальним розподілом D Детермінована тривалість G Випадкова тривалість обслуговування з довільним розподілом
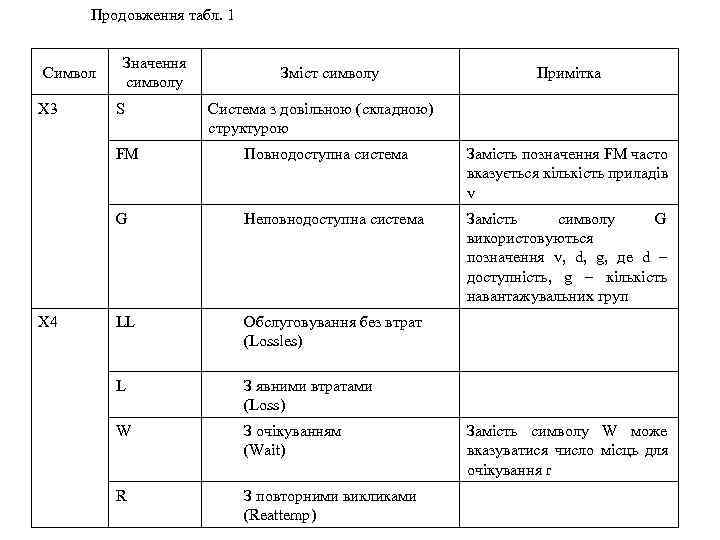
 Продовження табл. 1 Значення Символ Зміст символу Примітка символу X 3 S Cистема з довільною (складною) структурою FM Повнодоступна система Замість позначення FM часто вказується кількість приладів v G Неповнодоступна система Замість символу G використовуються позначення v, d, g, де d – доступність, g – кількість навантажувальних груп X 4 LL Обслуговування без втрат (Lossles) L З явними втратами (Loss) W З очікуванням Замість символу W може (Wait) вказуватися число місць для очікування r R З повторними викликами (Reattemp)
Продовження табл. 1 Значення Символ Зміст символу Примітка символу X 3 S Cистема з довільною (складною) структурою FM Повнодоступна система Замість позначення FM часто вказується кількість приладів v G Неповнодоступна система Замість символу G використовуються позначення v, d, g, де d – доступність, g – кількість навантажувальних груп X 4 LL Обслуговування без втрат (Lossles) L З явними втратами (Loss) W З очікуванням Замість символу W може (Wait) вказуватися число місць для очікування r R З повторними викликами (Reattemp)
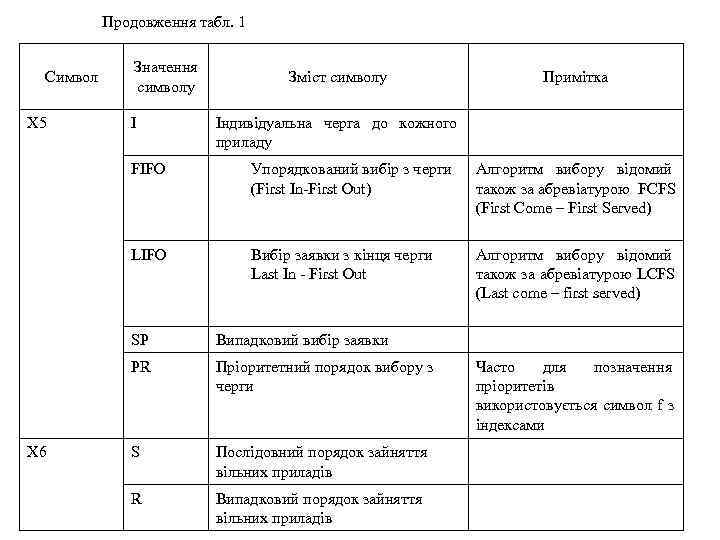
 Продовження табл. 1 Значення Символ Зміст символу Примітка символу X 5 I Індивідуальна черга до кожного приладу FIFO Упорядкований вибір з черги Алгоритм вибору відомий (First In-First Out) також за абревіатурою FCFS (First Come – First Served) LIFO Вибір заявки з кінця черги Алгоритм вибору відомий Last In - First Out також за абревіатурою LCFS (Last come – first served) SP Випадковий вибір заявки PR Пріоритетний порядок вибору з Часто для позначення черги пріоритетів використовується символ f з індексами X 6 S Послідовний порядок зайняття вільних приладів R Випадковий порядок зайняття вільних приладів
Продовження табл. 1 Значення Символ Зміст символу Примітка символу X 5 I Індивідуальна черга до кожного приладу FIFO Упорядкований вибір з черги Алгоритм вибору відомий (First In-First Out) також за абревіатурою FCFS (First Come – First Served) LIFO Вибір заявки з кінця черги Алгоритм вибору відомий Last In - First Out також за абревіатурою LCFS (Last come – first served) SP Випадковий вибір заявки PR Пріоритетний порядок вибору з Часто для позначення черги пріоритетів використовується символ f з індексами X 6 S Послідовний порядок зайняття вільних приладів R Випадковий порядок зайняття вільних приладів
 Основні задачі теорії розподілу інформації • Основна мета теорії розподілу інформації полягає в розробці методів оцінювання якості функціонування систем розподілу інформації (СРІ). • Основними задачами теорії розподілу інформації є задача аналізу СРІ і задача синтезу СРІ. • Задача аналізу СРІ полягає у знаходженні залежностей і значень величин, що характеризують якість обслуговування, від характеристик і параметрів вхідного потоку викликів, схеми й дисципліни обслуговування. • У початковий період розвитку телефонної техніки задачі аналізу були актуальнішими, ніж задачі синтезу. • Задача синтезу полягає у визначенні структури і параметрів СРІ при заданих потоках, дисципліні і якості обслуговування. Ця задача є більш складною, ніж задача аналізу, і під час її вирішення, як правило, використовуються результати аналізу СРІ.
Основні задачі теорії розподілу інформації • Основна мета теорії розподілу інформації полягає в розробці методів оцінювання якості функціонування систем розподілу інформації (СРІ). • Основними задачами теорії розподілу інформації є задача аналізу СРІ і задача синтезу СРІ. • Задача аналізу СРІ полягає у знаходженні залежностей і значень величин, що характеризують якість обслуговування, від характеристик і параметрів вхідного потоку викликів, схеми й дисципліни обслуговування. • У початковий період розвитку телефонної техніки задачі аналізу були актуальнішими, ніж задачі синтезу. • Задача синтезу полягає у визначенні структури і параметрів СРІ при заданих потоках, дисципліні і якості обслуговування. Ця задача є більш складною, ніж задача аналізу, і під час її вирішення, як правило, використовуються результати аналізу СРІ.
 • Близькими до задач аналізу й синтезу є задачі оптимізації. Ці задачі виникають під час проектування СРІ і полягають у тому, щоб визначити такі значення параметрів СРІ, для яких при заданих потоках, якості й дисципліні обслуговування складність СРІ є мінімальною або ж при заданих потоках, дисципліні обслуговування, складності якісні показники функціонування системи розподілу інформації є найкращими. • Основними методами вирішення задач теорії розподілу інформації є аналітичний, чисельний і метод статистичного моделювання. • Аналітичні методи дозволяють вирішувати задачі теорії розподілу інформації в тих випадках, коли структура системи, характеристики потоку й дисципліна обслуговування відносно прості. При цьому розглядаються всі можливі стани системи, що обумовлені станом кожного елемента СРІ. Такі стани називаються мікростанами системи. Щоразу, коли надходить новий виклик або закінчується яка-небудь фаза роботи системи, вона змінює свій мікростан. Для кожного мікростану записується рівняння статистичної рівноваги. З розв`язку систем таких рівнянь знаходять точне вирішення задачі в межах прийнятої моделі.
• Близькими до задач аналізу й синтезу є задачі оптимізації. Ці задачі виникають під час проектування СРІ і полягають у тому, щоб визначити такі значення параметрів СРІ, для яких при заданих потоках, якості й дисципліні обслуговування складність СРІ є мінімальною або ж при заданих потоках, дисципліні обслуговування, складності якісні показники функціонування системи розподілу інформації є найкращими. • Основними методами вирішення задач теорії розподілу інформації є аналітичний, чисельний і метод статистичного моделювання. • Аналітичні методи дозволяють вирішувати задачі теорії розподілу інформації в тих випадках, коли структура системи, характеристики потоку й дисципліна обслуговування відносно прості. При цьому розглядаються всі можливі стани системи, що обумовлені станом кожного елемента СРІ. Такі стани називаються мікростанами системи. Щоразу, коли надходить новий виклик або закінчується яка-небудь фаза роботи системи, вона змінює свій мікростан. Для кожного мікростану записується рівняння статистичної рівноваги. З розв`язку систем таких рівнянь знаходять точне вирішення задачі в межах прийнятої моделі.
 • Для складних систем число мікростанів таке велике, що вирішити систему рівнянь статистичної рівноваги не можливо навіть за допомогою сучасних ЕОМ. Більш перспективним є так званий макропідхід. У складній системі з дуже великою кількістю мікростанів мікростани поєднуються в макростани. Для кожного макростану записується рівняння статистичної рівноваги. Внаслідок вирішення системи таких рівнянь знаходять точні або наближені формули для ймовірностей макростанів. • У багатьох випадках не вдається знайти аналітичне вирішення сформульованої задачі аналізу СРІ. Тоді можливе вирішення задачі аналізу СРІ за допомогою ЕОМ з використанням спеціальних алгоритмів, що дозволяють знаходити наближені рішення чисельними методами [1].
• Для складних систем число мікростанів таке велике, що вирішити систему рівнянь статистичної рівноваги не можливо навіть за допомогою сучасних ЕОМ. Більш перспективним є так званий макропідхід. У складній системі з дуже великою кількістю мікростанів мікростани поєднуються в макростани. Для кожного макростану записується рівняння статистичної рівноваги. Внаслідок вирішення системи таких рівнянь знаходять точні або наближені формули для ймовірностей макростанів. • У багатьох випадках не вдається знайти аналітичне вирішення сформульованої задачі аналізу СРІ. Тоді можливе вирішення задачі аналізу СРІ за допомогою ЕОМ з використанням спеціальних алгоритмів, що дозволяють знаходити наближені рішення чисельними методами [1].
 • Найбільш універсальним методом, що придатний для розв ’ язання задач практично будь-якої складності, є метод статистичного моделювання. Метод полягає в побудові математичної моделі системи, реалізація якого здійснюється у вигляді програми для ЕОМ. Моделювання дозволяє одержати чисельні результати, що характеризують якість обслуговування при заданих параметрах потоку, схеми й дисципліни обслуговування. Однак у силу специфіки методу він є менш зручним порівняно з аналітичним і чисельним методами під час визначення прихованих закономірностей функціонування або залежностей між окремими характеристиками системи. Крім того, для отримання достатньо точних результатів метод статистичного моделювання потребує великого обсягу обчислень. • У багатьох випадках розумне поєднання аналітичних і чисельних методів з методом статистичного моделювання дозволяє детально проаналізувати СРІ. При малих значеннях параметрів системи вдається одержати рішення точними аналітичними методами й проаналізувати граничні випадки при асимптотичній поведінці характеристик досліджуваної системи. Отримані висновки доповнюються результатами статистичного моделювання в області реальних значень параметрів системи.
• Найбільш універсальним методом, що придатний для розв ’ язання задач практично будь-якої складності, є метод статистичного моделювання. Метод полягає в побудові математичної моделі системи, реалізація якого здійснюється у вигляді програми для ЕОМ. Моделювання дозволяє одержати чисельні результати, що характеризують якість обслуговування при заданих параметрах потоку, схеми й дисципліни обслуговування. Однак у силу специфіки методу він є менш зручним порівняно з аналітичним і чисельним методами під час визначення прихованих закономірностей функціонування або залежностей між окремими характеристиками системи. Крім того, для отримання достатньо точних результатів метод статистичного моделювання потребує великого обсягу обчислень. • У багатьох випадках розумне поєднання аналітичних і чисельних методів з методом статистичного моделювання дозволяє детально проаналізувати СРІ. При малих значеннях параметрів системи вдається одержати рішення точними аналітичними методами й проаналізувати граничні випадки при асимптотичній поведінці характеристик досліджуваної системи. Отримані висновки доповнюються результатами статистичного моделювання в області реальних значень параметрів системи.
 Лекція 2 ПОТОКИ ВИКЛИКІВ Основні питання 1 Поняття потоків викликів і основні способи їхнього задання 2. Класифікація потоків викликів відповідно до їх властивостей 3. Основні класи потоків. Найпростіші потоки
Лекція 2 ПОТОКИ ВИКЛИКІВ Основні питання 1 Поняття потоків викликів і основні способи їхнього задання 2. Класифікація потоків викликів відповідно до їх властивостей 3. Основні класи потоків. Найпростіші потоки
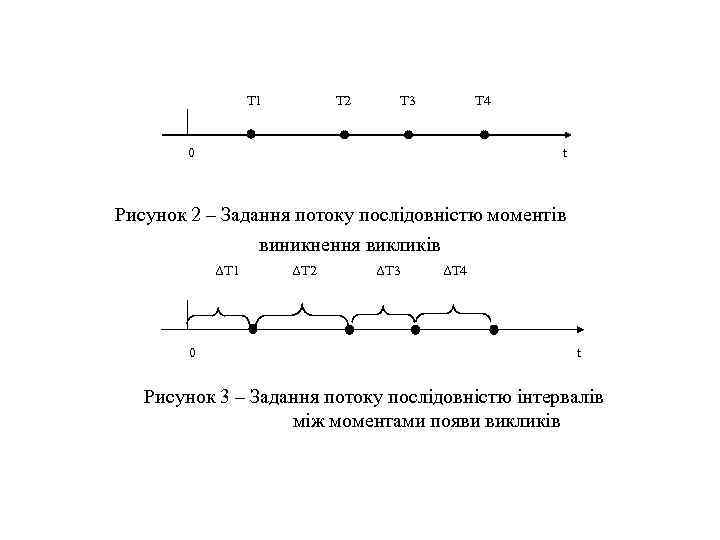
 Поняття потоків викликів і основні способи їхнього задання • Потоком викликів (заявок) називається послідовність викликів (заявок), що надходять на СРІ в деякі моменти часу [1 -5]. • Потоки можуть бути детермінованими або випадковими. • Детермінований потік – це потік викликів з фіксованими моментами їхнього надходження. Такий потік рідко зустрічається. • Якщо моменти надходження викликів залежать від випадкових факторів, то потік називається випадковим. Випадковий потік може бути заданий трьома еквівалентними способами: • 1) послідовністю моментів виникнення викликів (див. рис. 2); • 2) послідовністю інтервалів між сусідніми викликами (див. рис. 3); • 3) цілочисленним процесом, що визначає кількість викликів, які надійшли протягом часу [t 0, t) (див. рис. 4).
Поняття потоків викликів і основні способи їхнього задання • Потоком викликів (заявок) називається послідовність викликів (заявок), що надходять на СРІ в деякі моменти часу [1 -5]. • Потоки можуть бути детермінованими або випадковими. • Детермінований потік – це потік викликів з фіксованими моментами їхнього надходження. Такий потік рідко зустрічається. • Якщо моменти надходження викликів залежать від випадкових факторів, то потік називається випадковим. Випадковий потік може бути заданий трьома еквівалентними способами: • 1) послідовністю моментів виникнення викликів (див. рис. 2); • 2) послідовністю інтервалів між сусідніми викликами (див. рис. 3); • 3) цілочисленним процесом, що визначає кількість викликів, які надійшли протягом часу [t 0, t) (див. рис. 4).
 T 1 T 2 T 3 T 4 0 t Рисунок 2 – Задання потоку послідовністю моментів виникнення викликів ΔT 1 ΔT 2 ΔT 3 ΔT 4 0 t Рисунок 3 – Задання потоку послідовністю інтервалів між моментами появи викликів
T 1 T 2 T 3 T 4 0 t Рисунок 2 – Задання потоку послідовністю моментів виникнення викликів ΔT 1 ΔT 2 ΔT 3 ΔT 4 0 t Рисунок 3 – Задання потоку послідовністю інтервалів між моментами появи викликів
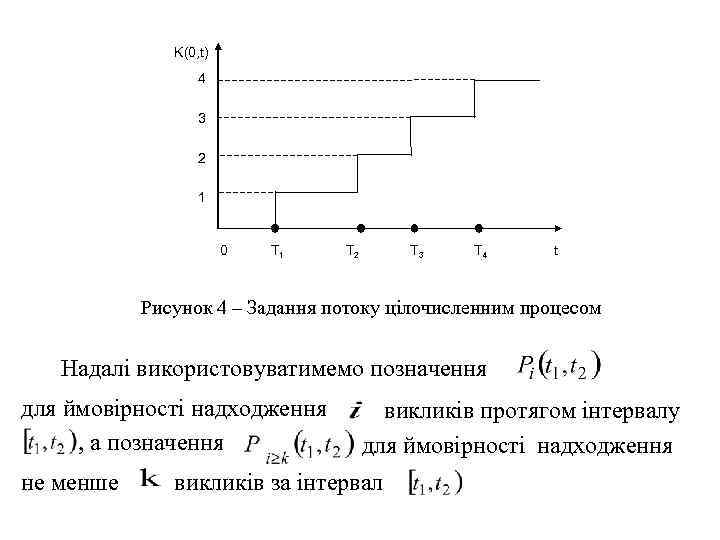
 K(0, t) 4 3 2 1 0 T 1 T 2 T 3 T 4 t Рисунок 4 – Задання потоку цілочисленним процесом Надалі використовуватимемо позначення для ймовірності надходження викликів протягом інтервалу , а позначення для ймовірності надходження не менше викликів за інтервал
K(0, t) 4 3 2 1 0 T 1 T 2 T 3 T 4 t Рисунок 4 – Задання потоку цілочисленним процесом Надалі використовуватимемо позначення для ймовірності надходження викликів протягом інтервалу , а позначення для ймовірності надходження не менше викликів за інтервал
 • Імовірнісний опис потоку викликів може бути виконаний з використанням багатовимірних функцій розподілу обраних характеристик потоку. • До основних числових характеристик потоків викликів належать: провідна функція потоку, інтенсивність і параметр потоку. • Провідною функцією потоку Λ(t) називається математичне очікування числа викликів, що надійшли за інтервал часу , тобто • Згідно з означенням, (1) Провідна функція невід’ємна й неспадна. Потоки з неперервною провідною функцією називаються регулярними, а зі східчастою – сингулярними.
• Імовірнісний опис потоку викликів може бути виконаний з використанням багатовимірних функцій розподілу обраних характеристик потоку. • До основних числових характеристик потоків викликів належать: провідна функція потоку, інтенсивність і параметр потоку. • Провідною функцією потоку Λ(t) називається математичне очікування числа викликів, що надійшли за інтервал часу , тобто • Згідно з означенням, (1) Провідна функція невід’ємна й неспадна. Потоки з неперервною провідною функцією називаються регулярними, а зі східчастою – сингулярними.
 • Під параметром потоку у момент часу розуміється величина (2) . Під інтенсивністю потоку розуміється середнє число викликів за одиницю часу: . (3) Для будь-яких потоків , причому для так званих ординарних потоків .
• Під параметром потоку у момент часу розуміється величина (2) . Під інтенсивністю потоку розуміється середнє число викликів за одиницю часу: . (3) Для будь-яких потоків , причому для так званих ординарних потоків .
 Класифікація потоків викликів відповідно до їх властивостей • Потоки викликів класифікуються згідно з такими властивостями, як однорідність, стаціонарність, ординарність і післядія. Розглянемо ці властивості. • 1. У неоднорідному потоці кожен виклик має дві і більше характеристики. Наприклад, виклики, що надходять від абонентів телефонної мережі, характеризуються моментами їхнього надходження, напрямками встановлення з'єднань, тривалістю обслуговування й іншими характеристиками. • Однорідний потік характеризується лише моментами надходження викликів. • На практиці потоки викликів, як правило, є неоднорідними. Однак у теорії розглядаються однорідні потоки, якщо відсутні спеціальні застереження. • 2. Властивість стаціонарності потоку означає, що його ймовірнісні характеристики не змінюються в часі.
Класифікація потоків викликів відповідно до їх властивостей • Потоки викликів класифікуються згідно з такими властивостями, як однорідність, стаціонарність, ординарність і післядія. Розглянемо ці властивості. • 1. У неоднорідному потоці кожен виклик має дві і більше характеристики. Наприклад, виклики, що надходять від абонентів телефонної мережі, характеризуються моментами їхнього надходження, напрямками встановлення з'єднань, тривалістю обслуговування й іншими характеристиками. • Однорідний потік характеризується лише моментами надходження викликів. • На практиці потоки викликів, як правило, є неоднорідними. Однак у теорії розглядаються однорідні потоки, якщо відсутні спеціальні застереження. • 2. Властивість стаціонарності потоку означає, що його ймовірнісні характеристики не змінюються в часі.
 • Потік викликів називається стаціонарним, якщо при будь- якому спільна ймовірність надходження викликів за інтервали часу …, не залежить від початкового моменту часу . Для стаціонарного потоку його параметр та інтенсивність постійні: . Потік, що не має властивості стаціонарності, називається нестаціонарним. 3. Потік викликів називається ординарним, якщо в ньому неможливе одночасне надходження двох і більше викликів, тобто виконується така умова: (4)
• Потік викликів називається стаціонарним, якщо при будь- якому спільна ймовірність надходження викликів за інтервали часу …, не залежить від початкового моменту часу . Для стаціонарного потоку його параметр та інтенсивність постійні: . Потік, що не має властивості стаціонарності, називається нестаціонарним. 3. Потік викликів називається ординарним, якщо в ньому неможливе одночасне надходження двох і більше викликів, тобто виконується така умова: (4)
 • Потік, що не має цієї властивості, називається неординарним. • Приклад ординарного потоку – потік викликів, що надходить на АТС від великої групи абонентів, а прикладами неординарних потоків є потоки телеграм у кілька адрес. • 4. Потік викликів називається потоком без післядії, якщо для будь-якого сумісна ймовірність надходження , викликів за відповідні інтервали , (5) не залежить від процесу надходження викликів до початкового моменту часу t.
• Потік, що не має цієї властивості, називається неординарним. • Приклад ординарного потоку – потік викликів, що надходить на АТС від великої групи абонентів, а прикладами неординарних потоків є потоки телеграм у кілька адрес. • 4. Потік викликів називається потоком без післядії, якщо для будь-якого сумісна ймовірність надходження , викликів за відповідні інтервали , (5) не залежить від процесу надходження викликів до початкового моменту часу t.
 • Іншими словами, відсутність післядії потоку означає незалежність плину випадкового потоку викликів після деякого моменту часу від його плину до цього моменту. • Прикладом потоку без післядії може служити потік телефонних викликів, що надходять від великої групи джерел. Це пов'язано з тим, що лише невелика частина (10 -20%) абонентської групи водночас бере участь у з'єднаннях. • Потоки, які не мають властивості відсутності післядії, називаються потоками з післядією. • Потоки викликів від спарених телефонних апаратів і потоки викликів від малих абонентських груп є прикладами потоків з післядією.
• Іншими словами, відсутність післядії потоку означає незалежність плину випадкового потоку викликів після деякого моменту часу від його плину до цього моменту. • Прикладом потоку без післядії може служити потік телефонних викликів, що надходять від великої групи джерел. Це пов'язано з тим, що лише невелика частина (10 -20%) абонентської групи водночас бере участь у з'єднаннях. • Потоки, які не мають властивості відсутності післядії, називаються потоками з післядією. • Потоки викликів від спарених телефонних апаратів і потоки викликів від малих абонентських груп є прикладами потоків з післядією.
 Основні класи потоків Найпростіші потоки • Найпростішим потоком називається стаціонарний ординарний потік без післядії. Цей потік є основною моделлю в теорії телетрафіку. • Для найпростішого потоку справедлива теорема. • Теорема 1. Надходження викликів за інтервал часу тривалістю у найпростішому потоці підпорядковується розподілу Пуассона з імовірностями , (6) де – імовірність того, що за інтервал часу довжиною надійде викликів; – параметр найпростішого потоку.
Основні класи потоків Найпростіші потоки • Найпростішим потоком називається стаціонарний ординарний потік без післядії. Цей потік є основною моделлю в теорії телетрафіку. • Для найпростішого потоку справедлива теорема. • Теорема 1. Надходження викликів за інтервал часу тривалістю у найпростішому потоці підпорядковується розподілу Пуассона з імовірностями , (6) де – імовірність того, що за інтервал часу довжиною надійде викликів; – параметр найпростішого потоку.
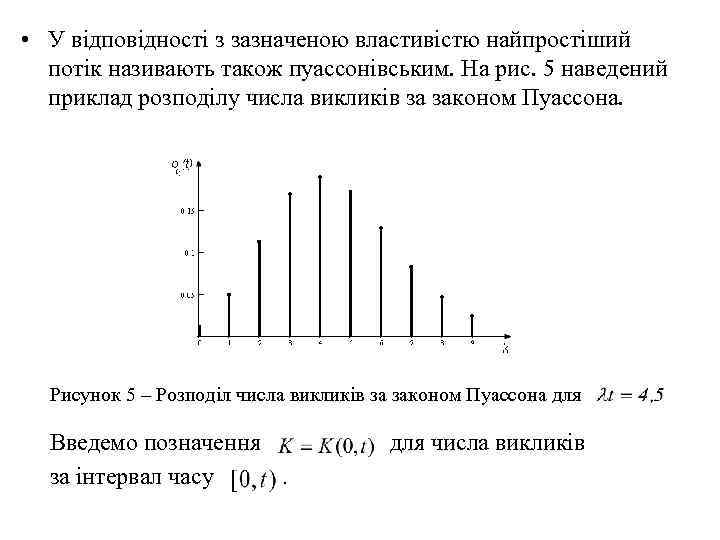
 • У відповідності з зазначеною властивістю найпростіший потік називають також пуассонівським. На рис. 5 наведений приклад розподілу числа викликів за законом Пуассона. Рисунок 5 – Розподіл числа викликів за законом Пуассона для Введемо позначення для числа викликів за інтервал часу .
• У відповідності з зазначеною властивістю найпростіший потік називають також пуассонівським. На рис. 5 наведений приклад розподілу числа викликів за законом Пуассона. Рисунок 5 – Розподіл числа викликів за законом Пуассона для Введемо позначення для числа викликів за інтервал часу .
 • Тоді із властивостей розподілу Пуассона випливають такі наслідки. • 1. . • 2. Імовірності пов'язані між собою рекурентним співвідношенням , , (7) де . 3. Послідовність імовірностей , з розподілу Пуассона при монотонно спадає зі зростанням . Якщо , то зі зростанням імовірності спочатку монотонно зростають до досягнення моди або двох модальних значень, а потім монотонно спадають.
• Тоді із властивостей розподілу Пуассона випливають такі наслідки. • 1. . • 2. Імовірності пов'язані між собою рекурентним співвідношенням , , (7) де . 3. Послідовність імовірностей , з розподілу Пуассона при монотонно спадає зі зростанням . Якщо , то зі зростанням імовірності спочатку монотонно зростають до досягнення моди або двох модальних значень, а потім монотонно спадають.
 • Якщо дрібне число, то мода , де – ціла частина числа , якщо ж ціле, то розподіл має дві моди: ; . 4. Зі зростанням добутку обвідна значень , наближається до нормального розподілу. Вже при =10 має місце добра апроксимація такої обвідної нормальним розподілом: (8)
• Якщо дрібне число, то мода , де – ціла частина числа , якщо ж ціле, то розподіл має дві моди: ; . 4. Зі зростанням добутку обвідна значень , наближається до нормального розподілу. Вже при =10 має місце добра апроксимація такої обвідної нормальним розподілом: (8)
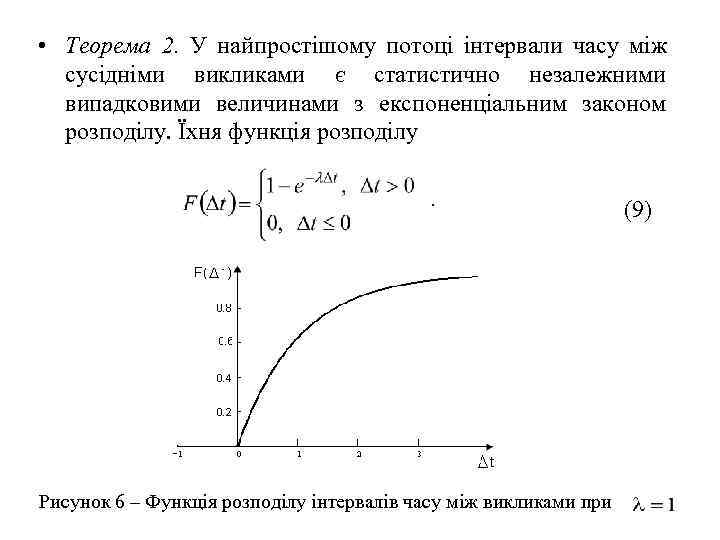
 • Теорема 2. У найпростішому потоці інтервали часу між сусідніми викликами є статистично незалежними випадковими величинами з експоненціальним законом розподілу. Їхня функція розподілу (9) Рисунок 6 – Функція розподілу інтервалів часу між викликами при
• Теорема 2. У найпростішому потоці інтервали часу між сусідніми викликами є статистично незалежними випадковими величинами з експоненціальним законом розподілу. Їхня функція розподілу (9) Рисунок 6 – Функція розподілу інтервалів часу між викликами при
 • Щільність імовірності експоненціального розподілу описується виразом , (10) а математичне очікування й дисперсія відповідно дорівнюють , . (11) Можна показати, що розподіл інтервалів часу між викликами за експоненціальним законом є не тільки необхідною, але й достатньою умовою для того, щоб потік був найпростішим. Експоненціальний закон має таку важливу властивість: якщо проміжок часу, розподілений за експоненціальним законом, тривав певний час, то це жодним чином не впливає на закон розподілу тієї частини, що залишилася від усього проміжку.
• Щільність імовірності експоненціального розподілу описується виразом , (10) а математичне очікування й дисперсія відповідно дорівнюють , . (11) Можна показати, що розподіл інтервалів часу між викликами за експоненціальним законом є не тільки необхідною, але й достатньою умовою для того, щоб потік був найпростішим. Експоненціальний закон має таку важливу властивість: якщо проміжок часу, розподілений за експоненціальним законом, тривав певний час, то це жодним чином не впливає на закон розподілу тієї частини, що залишилася від усього проміжку.
 Нестаціонарний пуассонівський потік викликів • Нестаціонарним пуассонівським потоком (або найпростішим потоком із змінним параметром) називається ординарний потік без післядії, у якого параметр залежить від часу . Для цього потоку ймовірність надходження заявок на інтервалі часу визначається формулою , (12)
Нестаціонарний пуассонівський потік викликів • Нестаціонарним пуассонівським потоком (або найпростішим потоком із змінним параметром) називається ординарний потік без післядії, у якого параметр залежить від часу . Для цього потоку ймовірність надходження заявок на інтервалі часу визначається формулою , (12)
 Потоки з обмеженою післядією • Потоком з обмеженою післядією називається потік, у якого послідовність інтервалів часу між сусідніми викликами являє собою послідовність незалежних випадкових величин. Такий потік викликів описується послідовністю функцій розподілу інтервалів між викликами. Окремими випадками потоку з обмеженою післядією є: . - рекурентний потік, що характеризується однаково розподіленими інтервалами між викликами ; (13) - рекурентний потік із запізнюванням, для якого ; . (14)
Потоки з обмеженою післядією • Потоком з обмеженою післядією називається потік, у якого послідовність інтервалів часу між сусідніми викликами являє собою послідовність незалежних випадкових величин. Такий потік викликів описується послідовністю функцій розподілу інтервалів між викликами. Окремими випадками потоку з обмеженою післядією є: . - рекурентний потік, що характеризується однаково розподіленими інтервалами між викликами ; (13) - рекурентний потік із запізнюванням, для якого ; . (14)
 Потоки з обмеженою післядією • У теорії надійності рекурентний потік називається процесом відновлення, а рекурентний потік із запізнюванням – загальним процесом відновлення.
Потоки з обмеженою післядією • У теорії надійності рекурентний потік називається процесом відновлення, а рекурентний потік із запізнюванням – загальним процесом відновлення.
 Потоки Пальма • Стаціонарний ординарний рекурентний потік із запізнюванням називається потоком Пальма. • Потоки Пальма описують виклики, загублені в СРІ. • Найпростіший потік є особливим випадком потоку Пальма, у якого всі проміжки часу між викликами, в тому числі і перший, мають експоненціальний розподіл. • Існує теорема Пальма, яка стверджує, що якщо на СРІ із втратами та експоненціальним законом розподілу тривалості обслуговування викликів надходять виклики, що утворять потік Пальма, то потік не обслужених викликів є потоком Пальма. Зокрема, якщо вихідний потік найпростіший, то потік загублених викликів буде потоком Пальма.
Потоки Пальма • Стаціонарний ординарний рекурентний потік із запізнюванням називається потоком Пальма. • Потоки Пальма описують виклики, загублені в СРІ. • Найпростіший потік є особливим випадком потоку Пальма, у якого всі проміжки часу між викликами, в тому числі і перший, мають експоненціальний розподіл. • Існує теорема Пальма, яка стверджує, що якщо на СРІ із втратами та експоненціальним законом розподілу тривалості обслуговування викликів надходять виклики, що утворять потік Пальма, то потік не обслужених викликів є потоком Пальма. Зокрема, якщо вихідний потік найпростіший, то потік загублених викликів буде потоком Пальма.
 Потоки Пальма • У теорії випадкових потоків показується, що для потоку Пальма випадкові величини мають неперервний розподіл із щільністю ймовірності (15) де , . (16) Для потоків Пальма (17)
Потоки Пальма • У теорії випадкових потоків показується, що для потоку Пальма випадкові величини мають неперервний розподіл із щільністю ймовірності (15) де , . (16) Для потоків Пальма (17)
 Потік Ерланга • Потоком Ерланга m-го порядку називається потік Пальма, в якому інтервали між сусідніми викликами – статистично незалежні випадкові величини, розподілені за законом Ерланга m-го порядку, тобто мають неперервний розподіл із щільністю ймовірності , (18) де λ – параметр розподілу Ерланга. Потік Ерланга відноситься до класу потоків з обмеженою післядією, для яких інтервали часу між сусідніми викликами є статично незалежними випадковими величинами з довільними й у загальному випадку різними законами розподілу.
Потік Ерланга • Потоком Ерланга m-го порядку називається потік Пальма, в якому інтервали між сусідніми викликами – статистично незалежні випадкові величини, розподілені за законом Ерланга m-го порядку, тобто мають неперервний розподіл із щільністю ймовірності , (18) де λ – параметр розподілу Ерланга. Потік Ерланга відноситься до класу потоків з обмеженою післядією, для яких інтервали часу між сусідніми викликами є статично незалежними випадковими величинами з довільними й у загальному випадку різними законами розподілу.
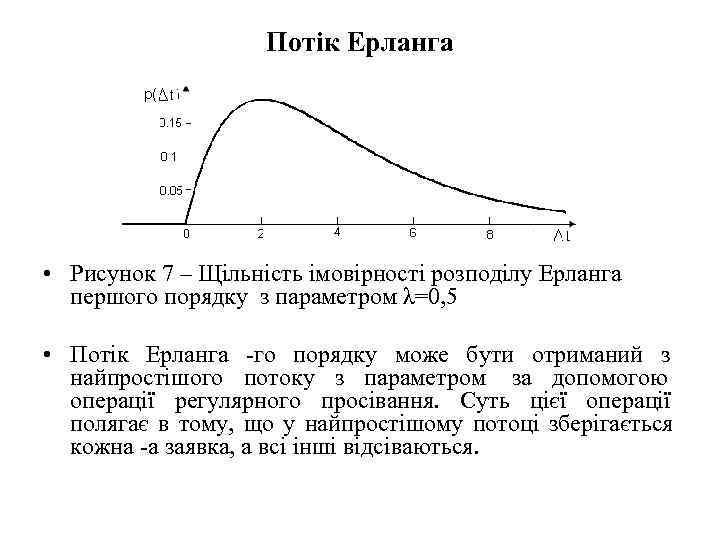
 Потік Ерланга • Рисунок 7 – Щільність імовірності розподілу Ерланга першого порядку з параметром λ=0, 5 • Потік Ерланга -го порядку може бути отриманий з найпростішого потоку з параметром за допомогою операції регулярного просівання. Суть цієї операції полягає в тому, що у найпростішому потоці зберігається кожна -а заявка, а всі інші відсіваються.
Потік Ерланга • Рисунок 7 – Щільність імовірності розподілу Ерланга першого порядку з параметром λ=0, 5 • Потік Ерланга -го порядку може бути отриманий з найпростішого потоку з параметром за допомогою операції регулярного просівання. Суть цієї операції полягає в тому, що у найпростішому потоці зберігається кожна -а заявка, а всі інші відсіваються.
 Потік Ерланга • При m=0 розподіл Ерланга збігається з експоненціальним розподілом. • При m≥ 0 розподіл Ерланга має єдиний максимум у точці Δt=m/λ, тому що . (19) Математичне очікування й дисперсія інтервалу часу між сусідніми викликами в потоці Ерланга m- го порядку дорівнюють , (20) де λ – параметр розподілу.
Потік Ерланга • При m=0 розподіл Ерланга збігається з експоненціальним розподілом. • При m≥ 0 розподіл Ерланга має єдиний максимум у точці Δt=m/λ, тому що . (19) Математичне очікування й дисперсія інтервалу часу між сусідніми викликами в потоці Ерланга m- го порядку дорівнюють , (20) де λ – параметр розподілу.
 Потік Ерланга • Потоки Ерланга при різному порядку створюють потоки з різним ступенем випадковості: від найпростішого при m=0 до детермінованого при m=∞. • Модель потоку Ерланга застосовують для опису процесів у системах розподілу інформації, коли найпростіший потік викликів розділяється на m+1 напрямок згідно з операцією регулярного просіювання.
Потік Ерланга • Потоки Ерланга при різному порядку створюють потоки з різним ступенем випадковості: від найпростішого при m=0 до детермінованого при m=∞. • Модель потоку Ерланга застосовують для опису процесів у системах розподілу інформації, коли найпростіший потік викликів розділяється на m+1 напрямок згідно з операцією регулярного просіювання.
