Lecture № 1. 4. Calculation systems. Hexadecimal

Lecture № 1. 4. Calculation systems. Hexadecimal calculation system. At adjustment of hardware IBM or creation of the new program often there is a necessity to glance inside of a computer memory to estimate its current condition. But there all is filled by long followers of zero and ones — binary numbers. These sequences are very inconvenient for perception. In this connection binary numbers began to break into groups on four categories. It is possible to make sixteen various binary numbers of four zero and ones. For coding 4 bats 16 signs for what 10 figures of decimal system and 6 letters of the latin alphabet are used are necessary.

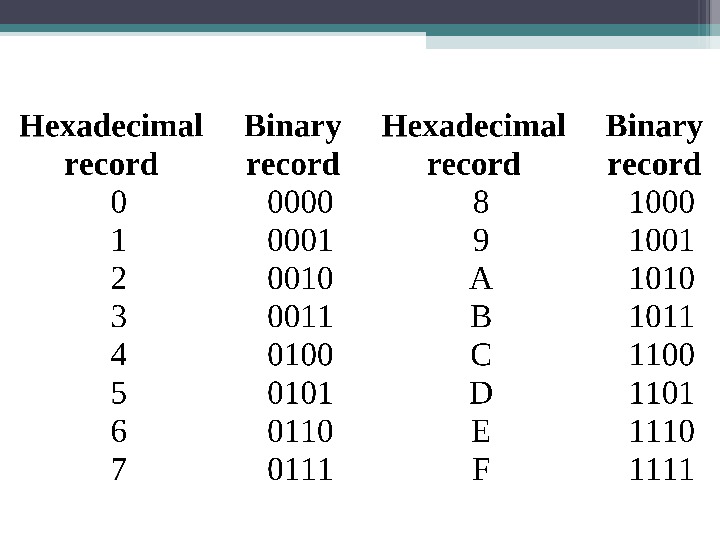
Each hexadecimal digit represents four binary digits (bits) also called a » nibble » Transition from hexadecimal system to binary (and back) is simple, binary nibbles are replaced with hexadecimal record. Example. The number В 3 16 to translate in binary calculation system В 3 16 =10110011 2 Example. The number 1111001110 2 to translate in hexadecimal calculation system 1111001110 2 =3 СЕ 16 So that to translate number from decimal calculation system in hexadecimal it is possible to take advantage of two ways: under the formula, (to multiply number on degrees of number 16) or to make consistently translation in binary calculation system, and then in hexadecimal calculation system. Example. The number 365 10 to translate into hexadecimal calculation system: 1 ) 365 10 =13× 16 0 +6× 16 1 +1× 16 2 =16 А 16 2 ) 365 10 =1× 2 0 +1× 2 2 +1× 2 3 +1× 2 5 +1× 2 6 +1× 2 8 =101101101 2 =16 А

Addition and subtraction in the hexadecimal calculation system. At performance of these actions in hexadecimal calculation system it is necessary to observe following rules: 1) at record of results of addition and subtraction it is necessary to use figures of the hexadecimal alphabet: the figures designating numbers from 10 up to 15 enter the name latin letters, therefore, if the result is number from this interval, it should be written down the corresponding latin letter; 2) 10 in hexadecimal calculation system is equal 16, i. e. overflow of the category acts, if the result of addition more or is equal 16, and in this case for record of result it is necessary to subtract 16, to write down the rest, and to the senior category to add unit of overflow; 3) if it is necessary to borrow unit in the senior category, this unit is transferred in younger category in the form of sixteen units.

As it has noted been above, the computer is capable to distinguish only values a bit: 0 or 1. However is more often it works with bytes (1 byte = 8 bits). All work of a computer is a management of bytes streams which direct in the machine from the keyboard or disks, are transformed on commands of programs, temporarily are filled or enter the name on constant storage, and also appear on the screen of the display or a paper of the printer in the form of familiar letters, figures, service signs. Byte it is more convenient to measure greater sets larger units: 1024 byte = 1 Kb (kilobyte) 1024 kilobytes (1048576 bytes) = 1 Mb (megabyte) What whole positive number can be written down in 1 byte? The Maximal binary number in eight-digit byte 1111 2 =255 10. If it is required to write down greater number some byte is required. From here it is visible, that together with 0 in one byte it is possible to write down 256 various decimal numbers.

This property byte helps to interpret pressing of any key, i. e. a combination of zero and unit (one byte) as decimal number from 0 up to 255. For the machine this number can serve as number of «letter» with the image of the pressed key which is stored in memory of the machine. Special electronic schemes under this number find «letter» and «print» it on the screen. To each letter, figure, a service sign any code — decimal number in a range from 0 up to 255 is appropriated. These codes are stored in the special code table which shares on two half (with codes from 0 up to 127 and from 128 up to 255). All over the world as the standard table ASCII which codes half of possible symbols — from 0 up to 127 is accepted. Second half of code table (codes from 128 up to 255) is intended for accommodation of symbols of national alphabets, pseudo-graphic symbols, some mathematical signs. It is necessary to know, that capital and lower case letters have different codes, and many latin and Russian letters have visually indiscernible tracings, but different codes (for example A). Example. The word the COMPUTER in codes will look as

Translation of numbers from one calculation system to another. While translating numbers from a decimal calculation system in system with basis P> 1 usually use following algorithm: 1) if the whole part of number it shares on P then the remainder of division is remembered is translated. Received private again shares on P, the rest is remembered. Procedure proceeds until private does not become equal to zero. Remainders of division on P leave by way of, to return their reception; 2) if the fractional part of number it is multiplied on P then the whole part is remembered and rejected is translated. Again received fractional part is multiplied on P, etc. Procedure proceeds until the fractional part does not become equal to zero. The whole parts leave after a binary comma by way of their reception. Result can be either final, or periodic binary fraction. Therefore, when the fraction is periodic, it is necessary to break multiplication to any step and to be content with the approached record of initial number in system with basis P.

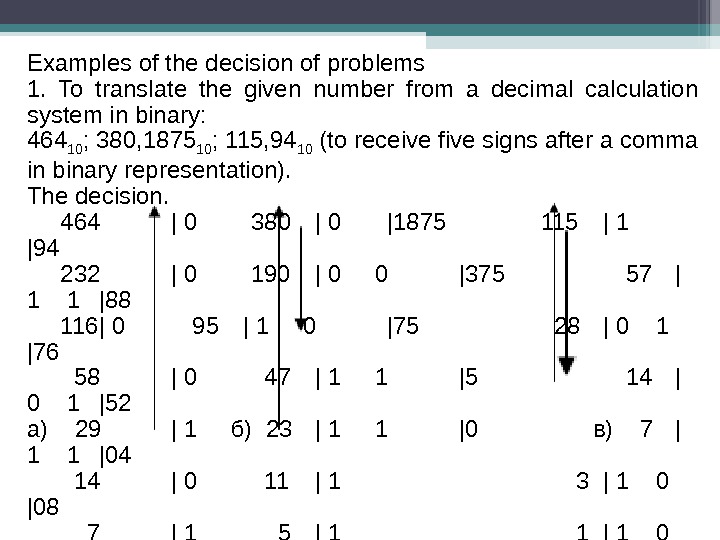
Examples of the decision of problems 1. To translate the given number from a decimal calculation system in binary: 464 10 ; 380, 1875 10 ; 115, 94 10 (to receive five signs after a comma in binary representation). The decision. 464 | 0 380 | 0 |1875 115 | 1 |94 232 | 0 190 | 0 0 |375 57 | 1 1 |88 116 | 0 95 | 1 0 |75 28 | 0 1 |76 58 | 0 47 | 1 1 |5 14 | 0 1 |52 а) 29 | 1 б) 23 | 1 1 |0 в) 7 | 1 1 |04 14 | 0 11 | 1 3 | 1 0 |08 7 | 1 5 | 1 1 | 1 0 |16 3 | 1 2 | 0 1 | 1 464 10 = 111010000 2 ; 380, 1875 10 = 101111100, 0011 2 ; 115, 94 10 = 1110011, 11110 2 (in the present case it has been received six signs after a comma then the result has been approximated).

If it is necessary to translate number from a binary calculation system in a calculation system which basis is the degree of the two, it is enough to unite figures of binary number in groups on so much figures, what exponent, and to use resulted below algorithm. For example, if translation is carried out in hexadecimal system groups will contain four figures (16 = 24). So, in the whole part we shall make a grouping from right to left, in fractional — from left to right. If in last group there are no figures, finish zero: in the whole part — at the left, in fractional — on the right. Then each group is replaced with the corresponding figure of new system. Conformity are resulted in tables.

Let’s translate from binary system in hexadecimal number 1111010101, 11 2. 0011 1101 0101, 1100 2 = 3 D 5, C 16. While translating numbers from a calculation system with basis P in a decimal calculation system it is necessary to number categories of the whole part from right to left, since zero, and in a fractional part, since the category right after a comma from left to right (initial number-1). Then to calculate the sum of products of corresponding values of categories on the basis of a calculation system in a degree equal to number of the category. It also is representation of initial number in a decimal calculation system. 2. To translate the given number in a decimal calculation system. a ) 1000001 2 =1× 2 6 +0× 2 5 +0× 2 4 +0× 2 3 +0× 2 2 +0× 2 1 +1× 2 0 =64+1=65 1 0. The remark. It is obvious, that if in any category there is a zero corresponding composed it is possible to lower.

b ) 1000011111, 01012. 1000011111, 0101 2 =1× 29 + 1× 24 + 1× 23 + 1× 22 + 1× 21 + 1× 20 + 1× 2 -2 + 1× 2 -4 = 512 + 16 + 8 + 4 + 2 + 1 + 0, 25 + 0, 0625 = 543, 3125 10. c ) 29 A, 5 16 =2× 162 +9× 161 +10× 160 +5× 16 -1 =512+144+10+0, 3125 = = 656, 3125 10. For performance of arithmetic operations in a calculation system with basis P it is necessary to have corresponding tables of addition and multiplication. For P = 2 and 16 tables are presented in lecture file.