L 13 Simple Harmonic Motion SHM LECTURE OUTLINE

L– 13 Simple Harmonic Motion (SHM) LECTURE OUTLINE 1. Periodic Motion: Simple Harmonic Motion 2. Motion of a Spring-Mass System 3. The Simple Pendulum 4. Mathematical Description of Simple Harmonic Oscillation 1

Project announcement • Each group is required to take distance v/s voltage readings (10 readings ) on your wind generator and plot a graph. • This is the last week to work on project.

1. Periodic motion: Simple Harmonic Motion SHM occurs when the net force is proportional to the displacement from the equilibrium point and is always directed toward the equilibrium point. i. e. it obeys Hooke’s law where F is the restoring force, x is the displacement and k is the spring constant (or 3 force constant)

Examples of SHM Not every periodic motion is SHM. However most periodic motions approximate to SHM for small displacements. Also assume no friction etc. - Mass on the end of a horizontal or vertical spring; - Simple and Compound pendula; - Vibrational motion of atoms and molecules in solids (amplitude depends on temperature). 4

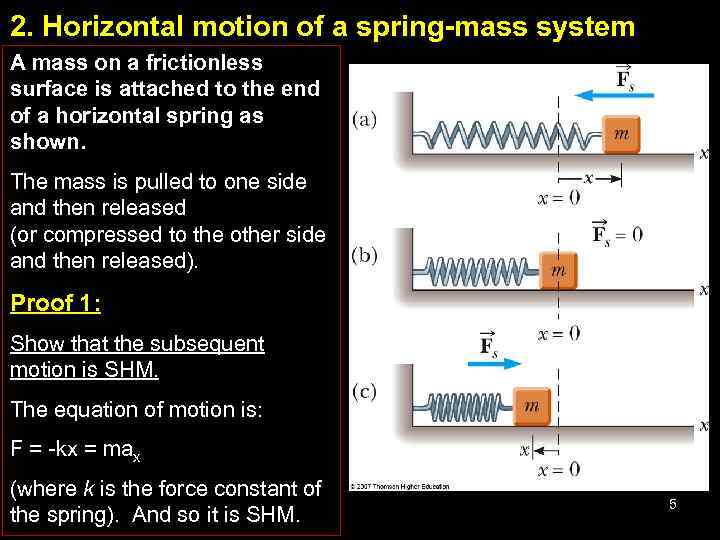2. Horizontal motion of a spring-mass system A mass on a frictionless surface is attached to the end of a horizontal spring as shown. The mass is pulled to one side and then released (or compressed to the other side and then released). Proof 1: Show that the subsequent motion is SHM. The equation of motion is: F = -kx = max (where k is the force constant of the spring). And so it is SHM. 5

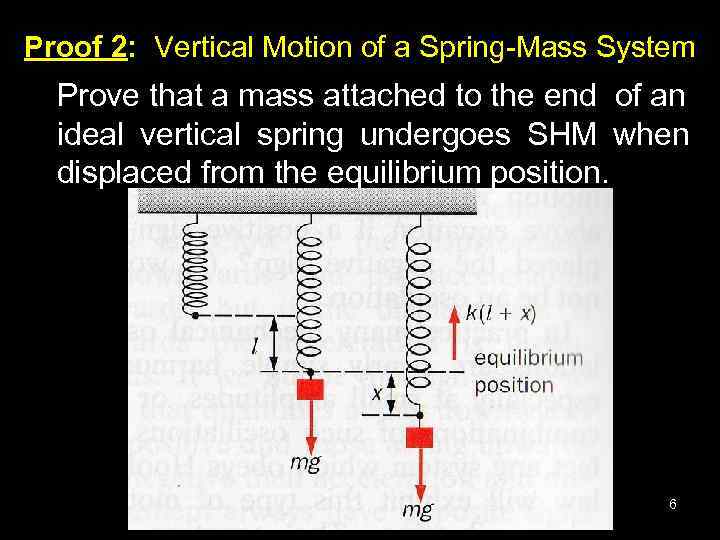Proof 2: Vertical Motion of a Spring-Mass System Prove that a mass attached to the end of an ideal vertical spring undergoes SHM when displaced from the equilibrium position. 6

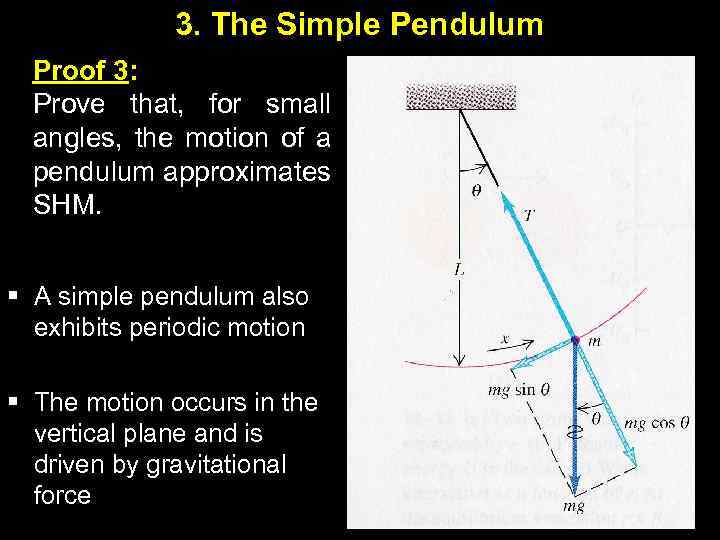3. The Simple Pendulum Proof 3: Prove that, for small angles, the motion of a pendulum approximates SHM. § A simple pendulum also exhibits periodic motion § The motion occurs in the vertical plane and is driven by gravitational force 7

4. Mathematical Description of Simple Harmonic Oscillation Basic equation of motion for SHM It is often convenient to write this as: where (ω is the angular frequency) This is a differential equation: 8

Proof 4: Prove that general solution for the equation has a form: Constants A and B depend on the initial conditions i. e. value of x and v when t = 0. The another possible form is φ – initial phase 9

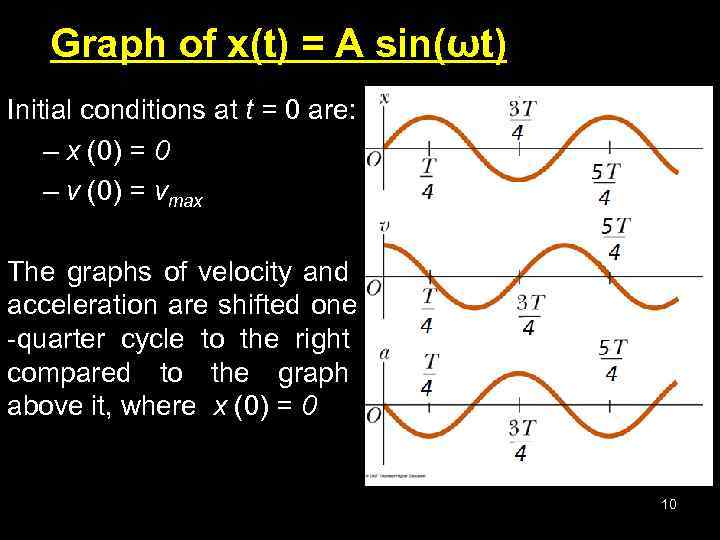Graph of x(t) = A sin(ωt) Initial conditions at t = 0 are: – x (0) = 0 – v (0) = vmax The graphs of velocity and acceleration are shifted one -quarter cycle to the right compared to the graph above it, where x (0) = 0 10

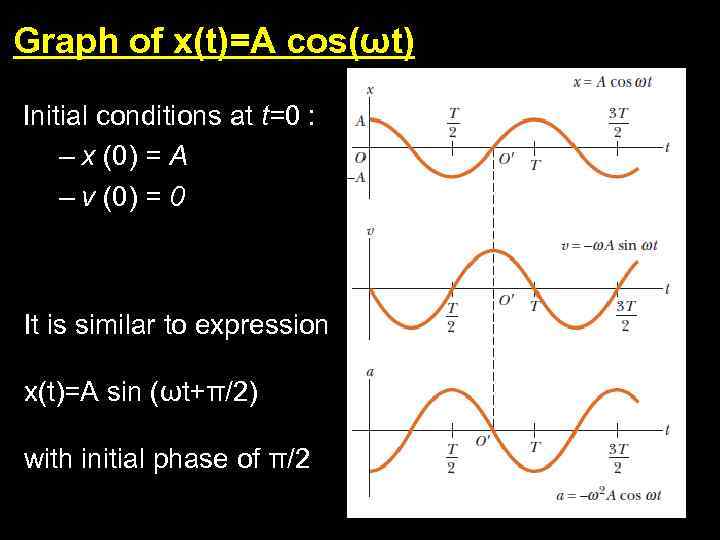Graph of x(t)=A cos(ωt) Initial conditions at t=0 : – x (0) = A – v (0) = 0 It is similar to expression x(t)=A sin (ωt+π/2) with initial phase of π/2 11

Physical meaning of this solution At t = 0 then x = 0, so the motion “starts” when the mass is passing through the equilibrium position x varies sinusoidally and the motion repeats with period and frequency ω is the angular frequency A is called the amplitude and is the maximum displacement. The maximum speed is vmax = Aω The maximum acceleration is amax = Aω2 12

For a spring Then And For a simple pendulum Then And 13

Example 1: A mass of 100 g is on a horizontal spring of constant k = 10. 0 Nm-1. It is initially displaced by 0. 100 m, and then released so that it oscillates. Assume friction is negligible. A) Find the amplitude, the period and the frequency of the SHM; B) Write down expressions for displacement, velocity and acceleration of SHM as functions 14 of time.

Example 2 An object in SHM has an amplitude A = 0. 200 cm and a frequency f = 20. 0 Hz. A) Write down expression for displacement as a function of time taking equilibrium point as initial position (x=0 at t=0); B) Find the velocity and acceleration of an object at x = 0; x = A and x = - A. 15

Ｖelocity v and acceleration a in terms of displacement acceleration velocity Find v 2 in terms of displacement, not time 16

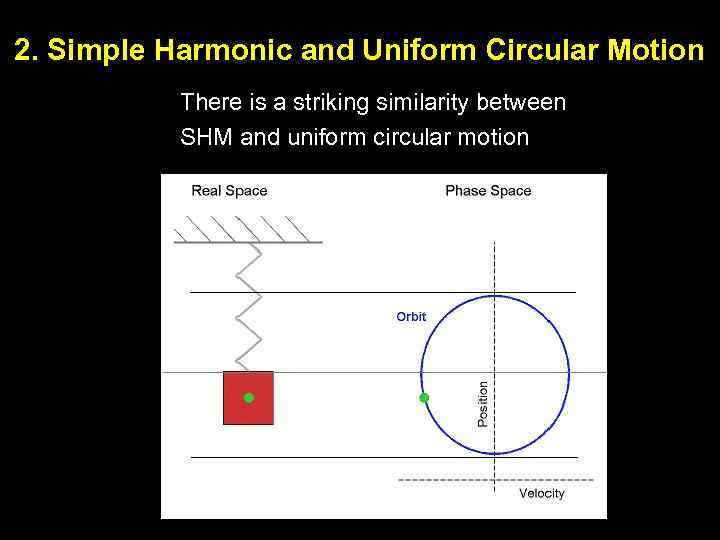2. Simple Harmonic and Uniform Circular Motion There is a striking similarity between SHM and uniform circular motion 17

Animations for Simple and physical pendulum See animations at: http: //wps. aw. com/aw_young_physics_11/13/3510/898588. c w/nav_and_content/index. html Animation 9. 10: Shows independence of period on mass, and dependence on length Animation 9. 12: A comparison between a simple and a uniform compound pendulum of same mass m. • Do they have the same period? • If no, which one do you expect to have the shortest period? 18

READING: - Adams and Allday, 3. 35, 3. 36 - Serway, Chapter 13, Sections 13. 1 -13. 4 LECTURE CHECK LIST • Understand what is meant by a differential equation (DE); • Be able to solve the DE for SHM by using a general solution; • Be able to solve problems using the equations of Simple Harmonic Motion. 19

ANSWERS Example 1 A) 0. 100 m; 0. 628 s; 1. 59 Hz; B) x=(0. 100 m) cos(10. 0 t) v=-(1. 00 m/s) sin(10. 0 t) a=-(10. 0 m/s 2) cos(10. 0 t) Example 2 i) x=(0. 200 cm)sin(12. 6 t); ii) 0. 251 m/s, 0 and 0; iii) 0, -31. 8 m/s² and 31. 8 m/s² 20