КВАДРАТИЧНЫЕ ФОРМЫ Квадратичной формой F зависящей от

КВАДРАТИЧНЫЕ ФОРМЫ Квадратичной формой F , зависящей от n переменных x 1, x 2, … , xn называется функция вида F = a 11 x 12 + 2 a 12 x 1 x 2 + a 22 x 22 + … + ann xn 2 = i, j= 1 n∑ aij xi xj , где aij = aji (i, j = 1, … , n) — вещественные числа. Симметричная матрица A = (aij) (i, j = 1, … , n) называется матрицей квадратичной формы F. Если переменные x 1, x 2, … , xn интерпретировать как координаты переменного вектора x в некотором ортонормированном базисе e 1, e 2, … , en n –мерного евклидова пространства, то матрица A есть матрица некоторого самосопряженного оператора ^A в этом базисе.

i, j= 1 n∑ aij xi xj = (^Ax, x). Действительно, пусть x = i= 1 n∑ xi ei и его образ y = ^A x. Тогда i–я координата образа yi = (^A x)i = j= 1 n∑ aijxj. Подставляя это выражение в формулу для скалярного произведения в ортонормированном базисе, получим (^Ax, x) = i= 1 n∑ xi yi = i, j= 1 n∑ aij xi xj = F Если рассматривать матрицу квадратичной формы как матрицу некоторого самосопряженного оператора, то, очевидно, ее вид будет зависеть от выбора базиса. Базис, в котором квадратичная форма F имеет вид F = i= 1 n∑ λi (xi')2(1) называется , а выражение (1) — квадратичной формы.

У всякого самосопряженного оператора существует ортонормированный базис из собственных векторов f 1, f 2, … , fn , соответствующих собственным значениям λ 1, λ 2, … , λn (среди которых могут быть равные). В этом базисе f 1, f 2, … , fn квадратичная форма относительно новых переменных x 1', x 2', … , xn' имеет канонический вид. Одна и та же квадратичная форма может быть приведена к каноническому виду многими способами, поэтому канонический вид определен неоднозначно.

Квадратичную форму F = i, j= 1 n∑ aij xi xj можно привести к каноническому виду с помощью ортогонального преобразования координат. Доказательство см. в книге О. В. Зиминой ``Линейная алгебра и аналитическая геометрия". Ортогональное преобразование в двумерном пространстве (на плоскости) есть либо поворот V 2 на угол j , либо отражение относительно оси, либо композиция этих операторов.

называется ранг ее матрицы. Если Rg A = n , квадратичная форма называется Если Rg A

Число слагаемых с положительными и отрицательными коэффициентами в каноническом виде квадратичной формы постоянно и не зависит от способа приведения формы к каноническому виду (т. е. от выбора собственного базиса).

Пример 1. Найдем матрицу квадратичной формы F = 2 x 12 − 4 x 1 x 2 + x 22 + 2 x 1 x 3 − x 32. Решение. 1. Запишем квадратичную форму F в виде: F = 2 x 12 − 2 x 1 x 2 − 2 x 1 + x 22 + x 1 x 3 + x 3 x 1 − x 32. 2. Матрица этой квадратичной формы есть 2 − 2 1 A = − 2 1 0 1 − 1 0

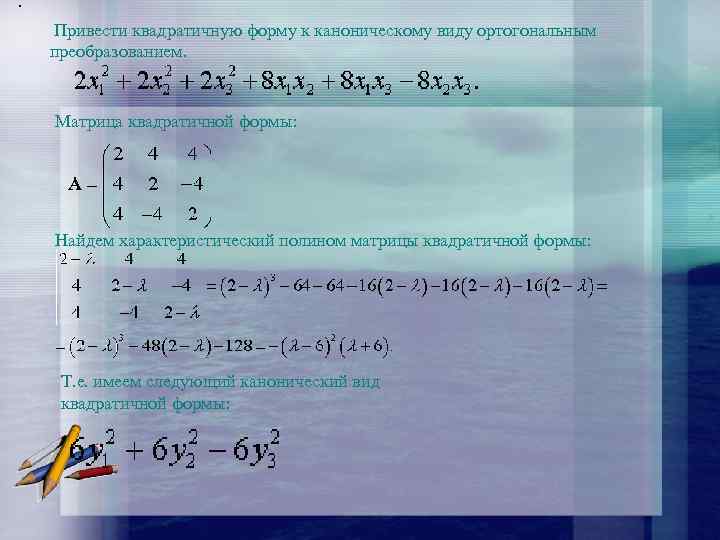. Привести квадратичную форму к каноническому виду ортогональным преобразованием. Матрица квадратичной формы: Найдем характеристический полином матрицы квадратичной формы: Т. е. имеем следующий канонический вид квадратичной формы: