КУРС ИНФОРМАТИКА И МАТЕМАТИКА ЧАСТЬ 2 МАТЕМАТИКА

КУРС ИНФОРМАТИКА И МАТЕМАТИКА ЧАСТЬ 2. МАТЕМАТИКА

Статистика l Статистика – наука, которая изучает массовые общественные явления (прежде всего, социально-экономические), исследование которых связано с количественными характеристиками и выявлением присущих им закономерностей. Предметом статистики являются общие вопросы измерения и анализа массовых количественных отношений и взаимосвязей.

Статистика l Иногда под статистикой понимают также и статистические данные: l l l l статистика торговли, судебная статистика, статистика занятости, демографическая статистика (статистика населения), медицинская статистика, транспортная статистика, статистика труда и т. д.

Математическая статистика l l Раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных. Математическая статистика тесно связана с теорией вероятностей, изучающей случайные события и случайные процессы.

Теория вероятностей l l Вероятность – числовая характеристика (мера) возможности появления какого-либо определенного события в тех или иных определенных условиях, которые могут повторяться неограниченное число раз. Вероятность принимает значения в интервале [0; 1] или [0%, 100%].

Теория вероятностей l l Событие, которое наступает в определенных условиях всегда, имеет вероятность 1 или 100%. Оно называется достоверным. Событие, которое не наступает в определенных условиях никогда, имеет вероятность 0. Оно называется невозможным.

Теория вероятностей l l На практике представление о вероятности события дает относительная частота (доля) его появления в серии с конечным числом испытаний. Чем больше число испытаний, тем ближе значение частоты к вероятности.

МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Введение

Основные понятия l l Математическая статистика имеет дело с совокупностью объектов, которые обладают некоторым набором признаков (показателей, характеристик). Это т. н. статистическая совокупность. Статистическая совокупность может включать все изучаемые объекты (в этом случае она называется генеральной совокупностью) или только часть объектов (тогда она называется выборкой).

Типы признаков l В связи с возможностью измерения все признаки принято делить на две большие группы: количественные и качественные.

Типы признаков l Наиболее часто в статистике используются количественные признаки. Примеры? l Количественный признак может быть измерен для каждого объекта числом. Каким образом?

Типы признаков l l Качественные признаки не могут быть измерены количественно для каждого объекта. Они указывают (обычно в текстовой форме) категорию, к которой относится тот или иной объект. Примеры? Однако качественные признаки также допускают измерение. Каким образом?

Дескриптивная статистика

Дескриптивная статистика l l Для более глубокого исследования материала необходимы количественные показатели, раскрывающие общие свойства статистической совокупности. Дескриптивная, или описательная, статистика позволяет заменить совокупность индивидуальных значений каждого показателя некоторыми общими для всех объектов величинами.

Дескриптивная статистика l Эти обобщенные показатели: l l l показывают тенденцию развития процесса или явления; позволяют сравнивать различные совокупности; используются во всех разделах математической статистики.

Основные статистические характеристики l Основные статистические характеристики можно разделить на две группы: l меры среднего уровня и l меры рассеяния (разброса).

Основные статистические характеристики l Меры среднего уровня дают усредненную характеристику совокупности объектов по определенному признаку. l Меры рассеяния показывают, насколько хорошо средние значения представляют данную совокупность.

Меры среднего уровня l К мерам среднего уровня относятся: l l l среднее (арифметическое) значение (обозначается Mean или ) , мода (обозначается Mo), медиана (обозначается Median или Mе).

Среднее арифметическое значение l Среднее арифметическое значение – это сумма значений признака у всех объектов совокупности, отнесенная к общему числу объектов: где - значение признака у i-го объекта, n – число объектов в совокупности.

Среднее арифметическое значение l Пример 1. Значения возраста в совокупности (группе) из 5 человек равны 30, 35, 30, 40 и 30 лет. Чему равен средний возраст?

Мода l l Мода – наиболее часто встречающееся значение признака в данной совокупности объектов. Пример 1. Значения возраста в группе из 5 человек равны 30, 35, 30, 40 и 30 лет. Чему равна мода?

Медиана l l Медиана – это "серединное" значение признака в том смысле, что у половины объектов значения этого признака меньше медианы, а у другой половины объектов – больше медианы. Для того, чтобы найти медиану, необходимо упорядочить все значения признака по возрастанию (или убыванию) и найти то число, которое находится в середине полученного ряда.

Медиана l Пример 1. Чему равна медиана для признака возраст в группе из пяти человек, которым 30, 35, 30, 40 и 30 лет?

Медиана l Пример 2. К группе добавили еще одного человека с возрастом 50 лет. Как подсчитать медиану?

Частотные распределения l Обычно предполагается, что исходные данные имеют вид таблицы "объектыпризнаки", т. е. каждый признак задается для каждого объекта. Это неудобно для больших совокупностей. Почему?

Частотные распределения l В этом случае полезно строить распределение признака, которое дает информацию о том, сколько раз встречаются различные значения (или интервалы значений) признака, т. е. каковы их частоты.

Частотные распределения l l Графическое изображение частотного распределения называется гистограммой. Гистограмма показывает зависимость частоты встречаемости признака от соответствующего значения или интервала группировки.

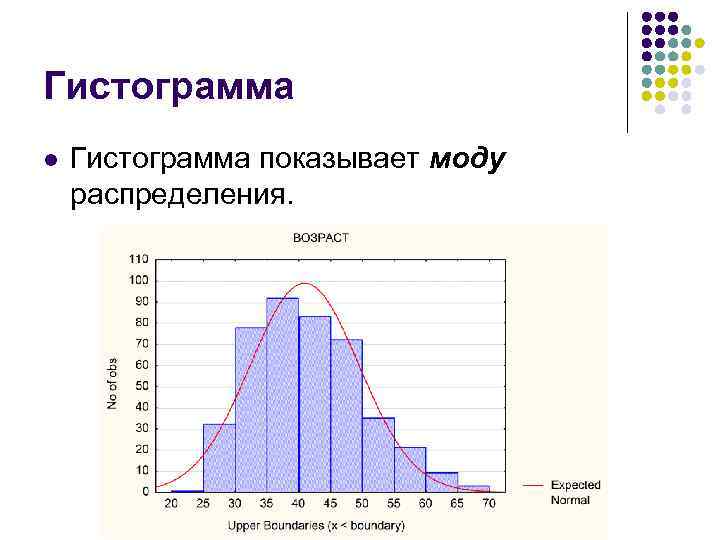Гистограмма l Гистограмма показывает моду распределения.

Гистограмма l Иногда наибольшую высоту могут иметь несколько столбиков. Например, распределение часто бывает бимодальным. Если мода имеет только одно значение, распределение называется унимодальным.

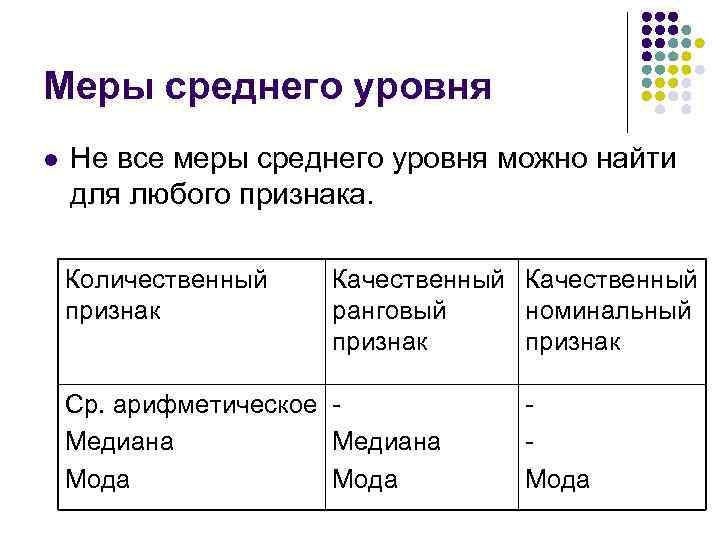Меры среднего уровня l Не все меры среднего уровня можно найти для любого признака. Количественный признак Качественный ранговый номинальный признак Ср. арифметическое Медиана Мода

Меры среднего уровня l В случае количественных данных все меры среднего уровня измеряются в тех же единицах, что и сам исходный признак. l Что произойдет, если все значения исходного признака изменятся в несколько раз? Что произойдет, если все значения исходного признака изменятся на некоторую величину? l

Меры среднего уровня l l Если распределение значений признака достаточно симметрично, все три меры среднего уровня (среднее арифметическое, медиана и мода) дают близкие значения. Если имеются значения, сильно отличающиеся от других, то они заметно влияют на среднее арифметическое ("притягивают" его к себе). В таком случае лучше использовать медиану, менее чувствительную к "выпадающим точкам".

Меры среднего уровня l Пример 3. Дан ряд значений: 30, 30, 35, 400. Найти среднее арифметическое значение, моду и медиану. Какое из трех значений лучше характеризует совокупность?

Меры рассеяния l l Все меры рассеяния показывают, насколько сильно варьируют значения признака (а точнее – их отклонения от среднего) в данной совокупности. Чем меньше значение меры разброса, тем ближе значения признака у всех объектов к своему среднему значению, а значит, и друг к другу. Чему должна быть равна величина меры разброса, если значения признака у всех объектов одинаковы?

Меры рассеяния l К мерам рассеяния относятся: l l l среднее квадратическое или стандартное отклонение – мера разброса значений признака около среднего арифметического значения (Std. Dev. – standard deviation или ). дисперсия признака ( 2) коэффициент вариации – отношение стандартного отклонения к среднему арифметическому (V, в процентах).

Среднее квадратическое отклонение l Величина среднего квадратического (или стандартного) отклонения вычисляется по формуле: l где - значение признака у i-го объекта, среднее арифметическое значение, n – число объектов в совокупности.

Среднее квадратическое отклонение l Среднее квадратическое отклонение измеряется, как и среднее арифметическое значение, в тех же единицах, что и сам исходный признак. l Что произойдет, если все значения признака изменить в несколько раз? Что произойдет если все значения признака увеличить (уменьшить) на некоторую величину? l

Коэффициент вариации l Коэффициент вариации вычисляется по формуле: l В отличие от среднего квадратического отклонения, коэффициент вариации измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности.

Коэффициент вариации l Пример 4. В первой группе средний доход в – 8 тыс. руб. , а во второй – 80 тыс. руб. l В первой группе среднее квадратическое отклонение для признака доход равно 4 тыс. руб. , а во второй – 20 тыс. руб. l Какая группа более однородна по величине дохода?

Коэффициент вариации l l l Если V не превышает 30%, совокупность объектов считается однородной по данному признаку. Если V превышает 50%, совокупность считается неоднородной. Такую совокупность разбивают на более однородные части. Если V находится в диапазоне 30 -50%, то решение об однородности принимает исследователь.

Меры рассеяния l l l Все меры рассеяния (среднее квадратическое отклонение, дисперсию и коэффициент вариации) можно вычислять только для количественных признаков. При этом величины среднего квадратического отклонения и дисперсии меняются при изменении единиц измерения признака, а величина коэффициента вариации – не изменяется. Коэффициент вариации может превышать 100%.