Круг. Окружность. Длина окружности. Площадь круга Гревцева Елизавета

Круг. Окружность. Длина окружности. Площадь круга Гревцева Елизавета 6 г

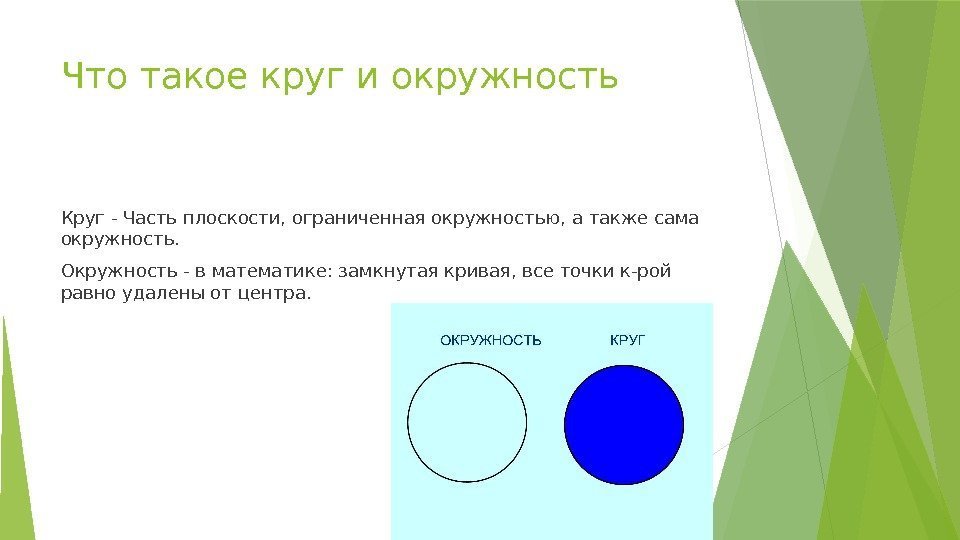Что такое круг и окружность Круг — Часть плоскости, ограниченная окружностью, а также сама окружность. Окружность — в математике: замкнутая кривая, все точки к-рой равно удалены от центра.

Что такое радиус и диаметр Радиус — Прямая линия, соединяющая центр с любой точкой окружности или поверхности шара. Диаметр — прямая линия, соединяющая две точки окружности и проходящая через центр.

Длина окружности 1. Формула для вычисления длины окружности через радиус: C = 2πr, где C – длина окружности, r – радиус окружности. То есть длина окружности равна удвоенному произведению радиуса на пи (π примерно равно 3, 14). 2. Подставьте данные вам значения в формулу и найдите длину окружности. Например, вы вырезаете полоску декоративной бумаги, чтобы обернуть ее вокруг пирога. Радиус пирога равен 50 см. Подставьте это значение в формулу. C = 2πr C = 2π x 50 C = 100π C = 314 см.

Площадь круга 1) Площадь круга равна произведению квадрата радиуса на число пи (3. 14). 2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус. S — площадь круга π — число пи (3. 1415) r — радиус круга