Кривые второго порядка.

Кривые второго порядка. 1

Определение. Алгебраической кривой 2 -го порядка называется линия, которая в некоторой Д. П. С. К. задается уравнением вида: (*) 2

Классификация кривых 2 -го порядка. Пусть в Д. П. С. К. задано уравнение второго порядка вида (*). Тогда существует такая Д. П. С. К. ( каноническая), в которой это уравнение примет один из следующих видов (каноническое уравнение): 1. Эллипс 3

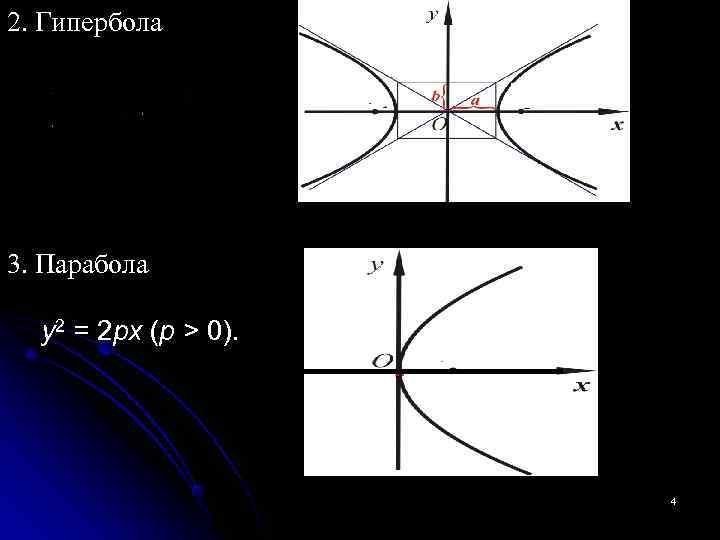
2. Гипербола 3. Парабола y 2 = 2 px (p > 0). 4

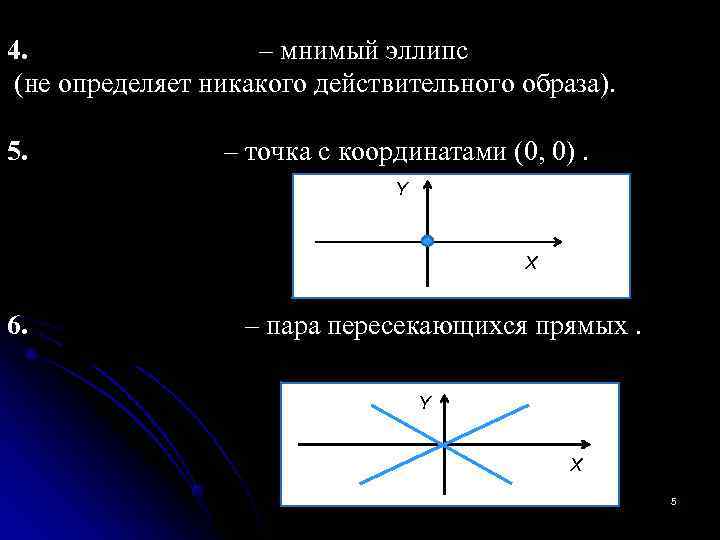
4. – мнимый эллипс (не определяет никакого действительного образа). 5. – точка с координатами (0, 0). Y X 6. – пара пересекающихся прямых. Y X 5

7. y 2 = b 2 – параллельных прямых. 8. y 2 = –b 2 – пара мнимых, параллельных прямых (не определяет никакого действительного образа). 9. y 2 = 0 – пара совпадающих прямых (ось OX). 6

Эллипс. Определение. Эллипсом называется кривая, которая в некоторой Д. П. С. К. определяется каноническим уравнением вида: B 2 Точки A 1(-a, 0), A 2(a, 0), B 1(0, A 2 -b), B 2(0, b) - вершины, A 1 a – большая полуось, b – малая полуось, O (0, 0)-центр эллипса (центр симметрии), B 1 оси OX, OY – оси симметрии. 7

расстояние от центра до фокусов, точки F 1(-c, 0), F 2(c, 0) – фокусы эллипса. - эксцентриситет эллипса. Так как c < a для эллипса, то Эксцентриситет характеризует степень вытянутости эллипса вдоль оси ОХ. Если значительно меньше чем а, то эллипс значительно вытянут вдоль оси ОХ. Таким образом, чем ближе эксцентриситет к единице, тем эллипс более вытянут вдоль оси ОХ. Если b=a, то и эллипс вырождается в окружность. 8 Для окружности c = 0 и оба фокуса совпадают с центром.

Прямые называются директрисами. Так как и директрисы проходят вне эллипса. Пусть М - произвольная точка на эллипсе, тогда векторы - фокальные радиус-векторы точки М, расстояние от любой точки М эллипса до фокусов F 1 и F 2 называются фокальными радиусами точки М и обозначаются r 1 и r 2. 9

Фокальное свойство эллипса. Сумма расстояний от любой точки М, лежащей на эллипсе, до фокусов есть величина постоянная и равная 2 а: Доказательство. Пусть точка M (x 0, y 0) – произвольная точка эллипса, F 1(-c, 0), F 2(c, 0) - фокусы. Тогда Точка M (x 0, y 0) лежит на эллипсе, 10

Тогда Аналогично, Так как то и 11

Пусть точка M (x 0 , y 0) такая, что Докажем, что точка M эллипсу. Избавимся от иррациональности в уравнении: 12

точка M эллипсу. 13

Фокальное свойство является определяющим для эллипса. Определение. Эллипсом называется геометрическое место точек на плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная. 14

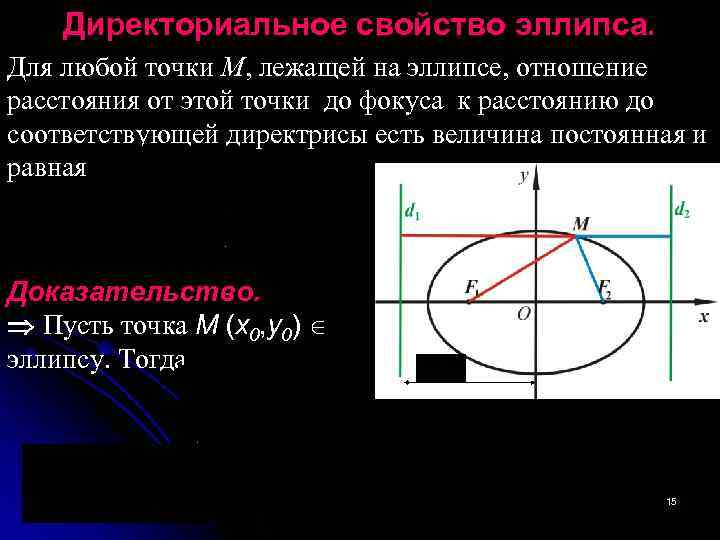
Директориальное свойство эллипса. Для любой точки М, лежащей на эллипсе, отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы есть величина постоянная и равная Доказательство. Пусть точка M (x 0, y 0) эллипсу. Тогда 15

Из фокального свойства эллипса: Пусть точка M (x 0 , y 0) такая, что 16

Избавимся от иррациональности в уравнении: 17

точка M эллипсу. 18

Аналогично, точка M эллипсу. Директориальное свойство является определяющим для эллипса. Определение. Эллипсом называется геометрическое место точек на плоскости, для каждой из которых отношение расстояния до некоторой фиксированной точки плоскости, называемой фокусом, к расстоянию до некоторой фиксированной прямой, соответствующей этому фокусу и называемой директрисой, равно некоторой 19 константе

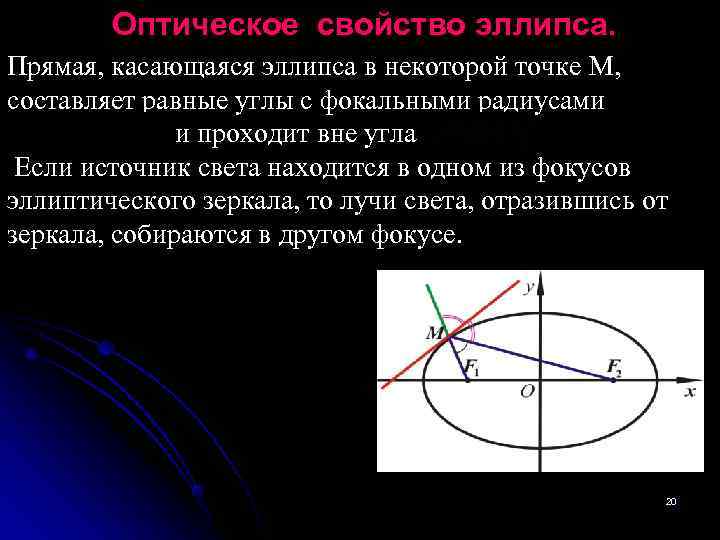
Оптическое свойство эллипса. Прямая, касающаяся эллипса в некоторой точке M, составляет равные углы с фокальными радиусами и проходит вне угла . Если источник света находится в одном из фокусов эллиптического зеркала, то лучи света, отразившись от зеркала, собираются в другом фокусе. 20

Гипербола. Определение. Гиперболой называется кривая, которая в некоторой Д. П. С. К. определяется каноническим уравнением вида: Из уравнения видно, что для любой точки M (x 0, y 0), B 2 лежащей на гиперболе A 2 то есть все точки гиперболы A 1 лежат вне вертикальной полосы шириной 2 a. B 1 Гипербола не пересекает ось ординат. A 1(-a, 0), A 2(a, 0) -вершины, a – действительная полуось, b – мнимая полуось, O(0, 0)- 21 центр симметрии, OX, OY – оси симметрии.

расстояние от центра до фокусов, F 1(-c, 0), F 2(c, 0) – фокусы гиперболы. - эксцентриситет. Так как c >a для гиперболы, то Прямые называются директрисами. Так как и директрисы проходят внутри гиперболы. Пусть М - произвольная точка на гиперболе. Векторы - фокальные радиус-векторы точки М, расстояние от любой точки М гиперболы до фокусов F 1 и 22 F 2 называются фокальными радиусами точки М.

Асимптоты гиперболы. Прямая линия называется асимптотой кривой, если расстояние от переменной точки на кривой до прямой стремится к нулю при неограниченном удалении точки кривой от начала координат. Покажем, что прямые являются асимптотами гиперболы. Расстояние от точки кривой до прямой стремится к нулю, если стремится к нулю разность ординат кривой и прямой. Из уравнения гиперболы находим: Покажем, что прямая является асимптотой ветви гиперболы Найдем предел: 23

Аналогично, можно показать, что прямая является асимптотой ветви гиперболы Утверждение. Произведение расстояний от точки, лежащей на гиперболе, до асимптот есть величина постоянная и равная Доказательство. Пусть точка M (x 0, y 0) – произвольная точка гиперболы, 24

25

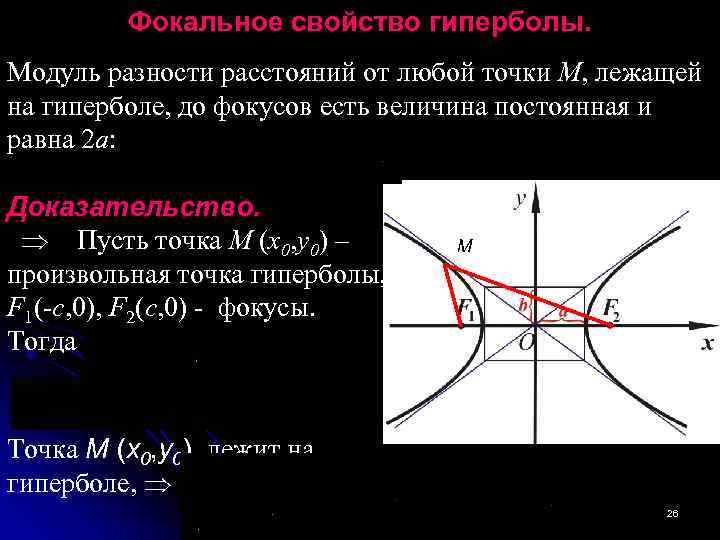
Фокальное свойство гиперболы. Модуль разности расстояний от любой точки М, лежащей на гиперболе, до фокусов есть величина постоянная и равна 2 а: Доказательство. Пусть точка M (x 0, y 0) – M произвольная точка гиперболы, F 1(-c, 0), F 2(c, 0) - фокусы. Тогда Точка M (x 0, y 0) лежит на гиперболе, 26

Тогда Аналогично, Так как то 27

Пусть точка M (x 0 , y 0) такая, что Докажем, что точка M гиперболе. Избавимся от иррациональности в уравнении: 28

29

M гиперболе. Фокальное свойство является определяющим для гиперболы. Определение. Гиперболой называется геометрическое место точек на плоскости, для которых модуль разности расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная и равна 2 а. 30

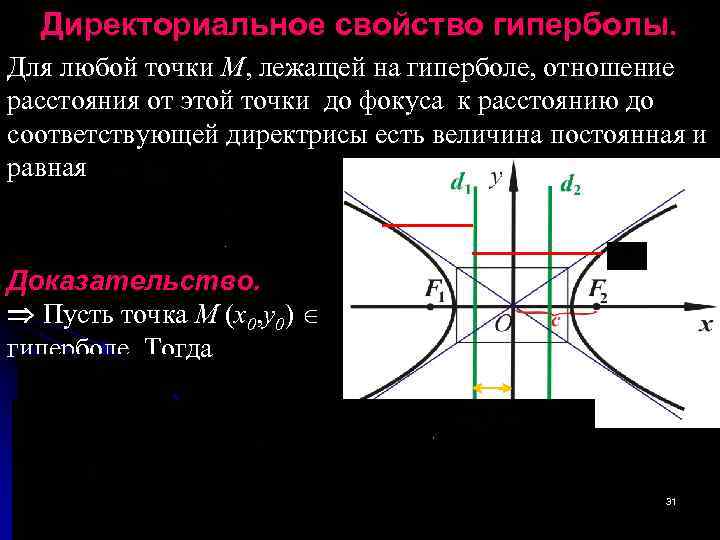
Директориальное свойство гиперболы. Для любой точки М, лежащей на гиперболе, отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы есть величина постоянная и равная Доказательство. Пусть точка M (x 0, y 0) гиперболе. Тогда 31

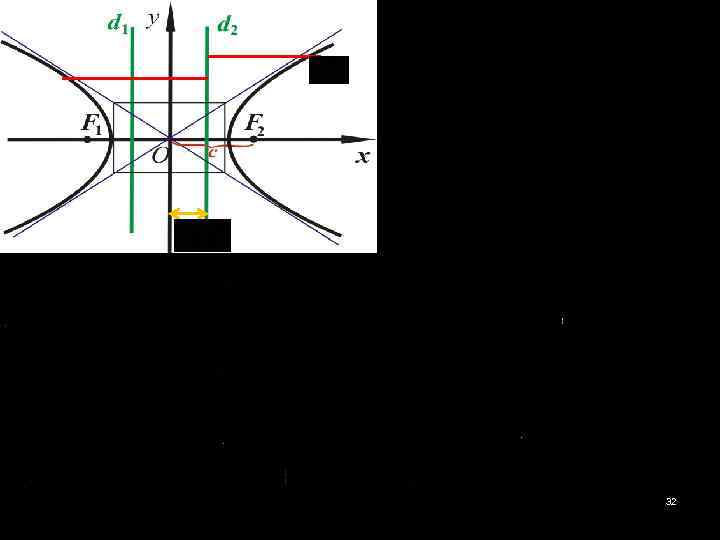
32

Тогда Пусть точка M (x 0 , y 0) такая, что 33

Избавимся от иррациональности в уравнении: 34

точка M гиперболе. 35

Аналогично, точка M гиперболе. Директориальное свойство является определяющим для гиперболы. Определение. Гиперболой называется геометрическое место точек на плоскости, для каждой из которых отношение расстояния до некоторой фиксированной точки плоскости, называемой фокусом, к расстоянию до некоторой фиксированной прямой, соответствующей этому фокусу и называемой директрисой, равно некоторой 36 константе

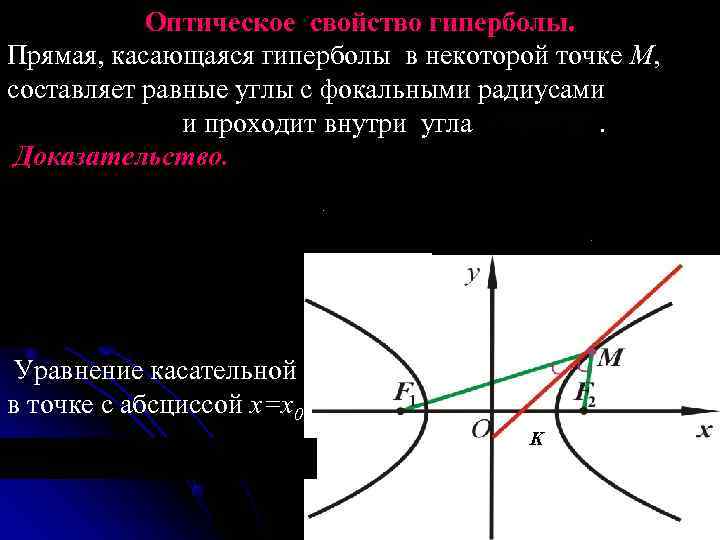
Оптическое свойство гиперболы. Прямая, касающаяся гиперболы в некоторой точке M, составляет равные углы с фокальными радиусами и проходит внутри угла . Доказательство. Уравнение касательной в точке с абсциссой x=x 0 K, 37

Напишем уравнение касательной в точке M (x 0 , y 0): Для правой ветви: Точка M (x 0 , y 0) лежит на гиперболе, следовательно, 38

Для левой ветви: уравнение касательной к гиперболе. 39

Найдем координаты точки K- точки пересечения касательной с осью абсцисс: по свойству биссектрисы угла получили, что MK-биссектриса угла в треугольнике касательная составляет равные углы с фокальными 40 радиусами.

Если источник света находится в одном из фокусов гиперболического зеркала, то лучи света, отразившись от зеркала, идут далее так, как если бы они исходили из другого фокуса. 41

Парабола. Параболой называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат имеет вид: y 2 = 2 px (p > 0). Число р – параметр; точка О(0, 0) – вершина параболы; ось OX – ось симметрии; точка – фокус. Пусть М(x 0, y 0) – произвольная точка, лежащая на параболе, тогда – фокальный радиус-вектор точки М. Прямая – директриса параболы. 42

Парабола не имеет центра симметрии. Так координата у входит в уравнение параболы в квадрате, то парабола симметрична относительно оси ОХ. При х=0 у=0, т. е. парабола проходит через начало координат. При Расстояние от любой точки параболы до фокуса называется фокальным радиусом точки и обозначается через r. 43

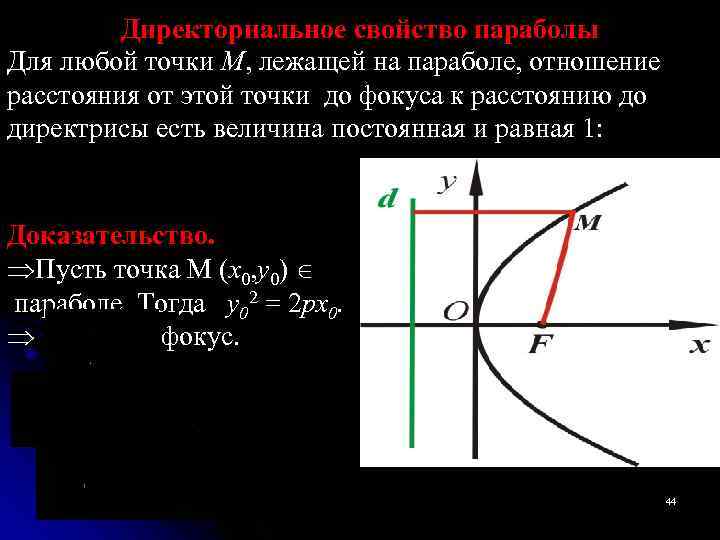
Директориальное свойство параболы Для любой точки М, лежащей на параболе, отношение расстояния от этой точки до фокуса к расстоянию до директрисы есть величина постоянная и равная 1: Доказательство. Пусть точка M (x 0, y 0) параболе. Тогда y 02 = 2 px 0. фокус. 44

так как p>0, x 0>0. Пусть точка M (x 0 , y 0) такая, что Покажем, что точка M лежит на параболе. Избавимся от иррациональности в уравнении: 45

точка M лежит на параболе. Определение. Параболой называется геометрическое место точек на плоскости, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. 46

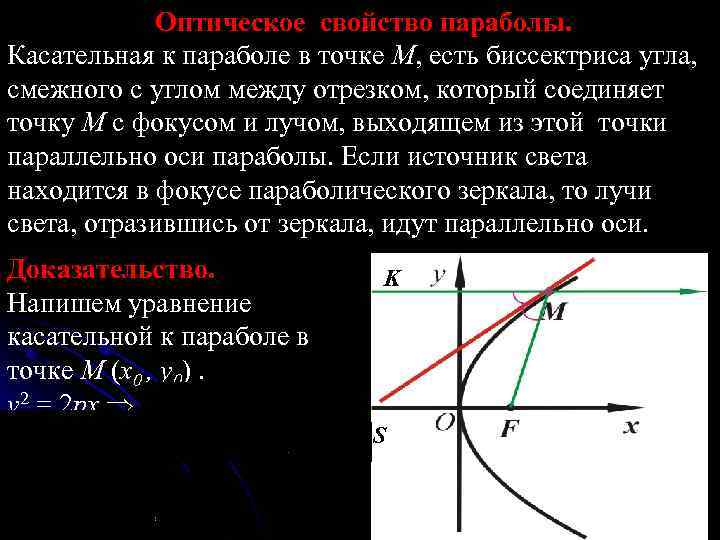
Оптическое свойство параболы. Касательная к параболе в точке M, есть биссектриса угла, смежного с углом между отрезком, который соединяет точку M с фокусом и лучом, выходящем из этой точки параллельно оси параболы. Если источник света находится в фокусе параболического зеркала, то лучи света, отразившись от зеркала, идут параллельно оси. Доказательство. K Напишем уравнение касательной к параболе в точке M (x 0 , y 0). y 2 = 2 px S 47

Так как уравнение касательной к параболе. Заметим, что вектор должен идти по биссектрисе угла KMF. 48

Найдем координаты точки S- точки пересечения касательной с осью абсцисс: Получили, что идущему по биссектрисе угла KMF. 49

Примеры. 1. Определить тип кривой , найти её основные параметры, сделать чертеж в данной ДПСК. Решение. Сгруппируем слагаемые и выделим полный квадрат по переменным х и y: Перейдем к новой декартовой прямоугольной системе координат X O Y , которая получается из исходной декартовой системы координат XOY параллельным переносом осей OX и OY: 50

Тогда – каноническое уравнение эллипса. Найдем основные параметры эллипса: a=3 - большая полуось, b=2– малая полуось, – расстояние от центра до фокуса; точки – фокусы, – эксцентриситет. Прямые и – директрисы. Найдем центр, вершины, фокусы, директрисы эллипса в исходной XOY системе координат, пользуясь формулами: и результаты запишем в таблицу: 51

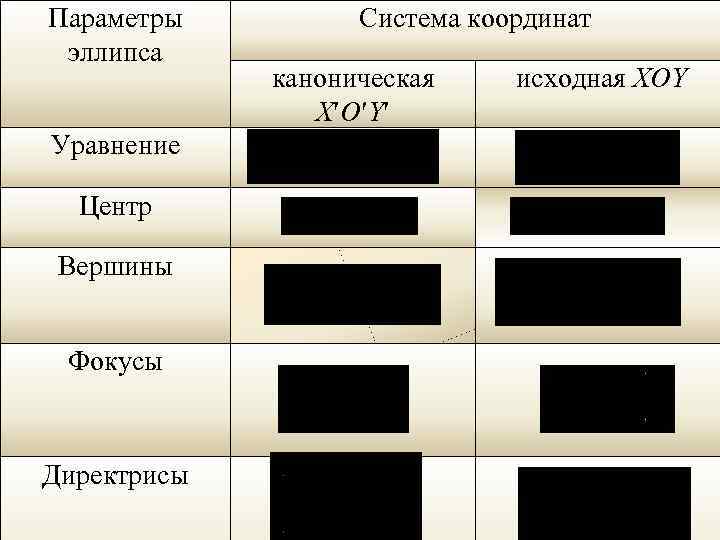
Параметры Система координат эллипса каноническая исходная XOY X O Y Уравнение Центр Вершины Фокусы Директрисы 52

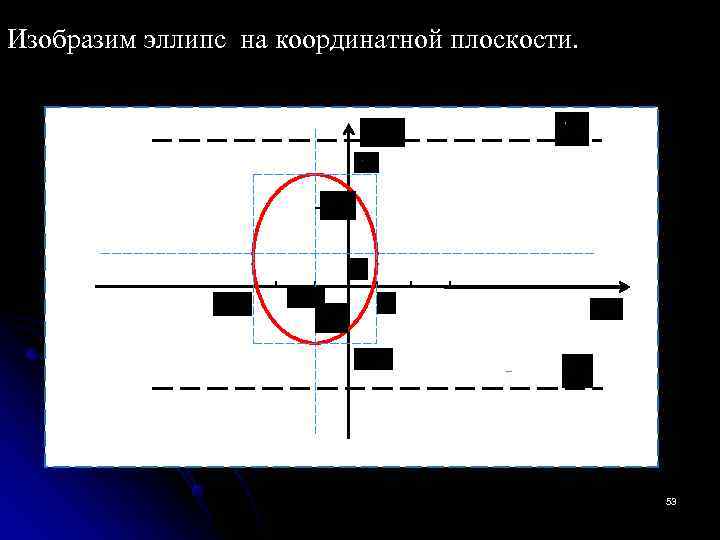
Изобразим эллипс на координатной плоскости. 53

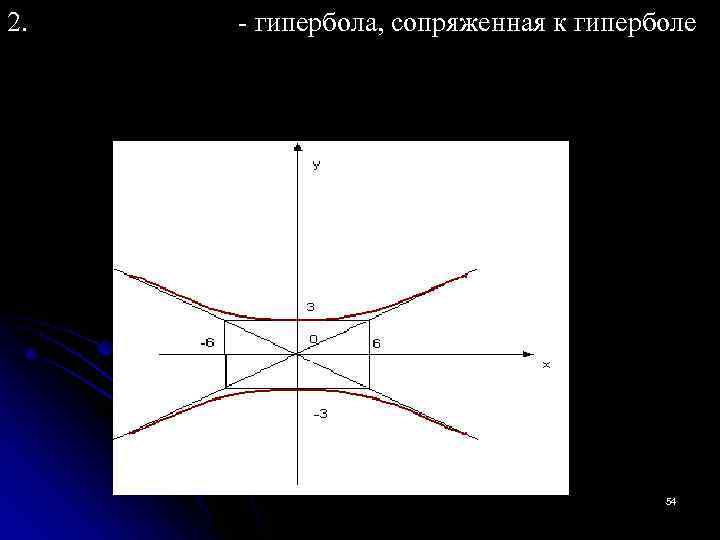
2. - гипербола, сопряженная к гиперболе 54

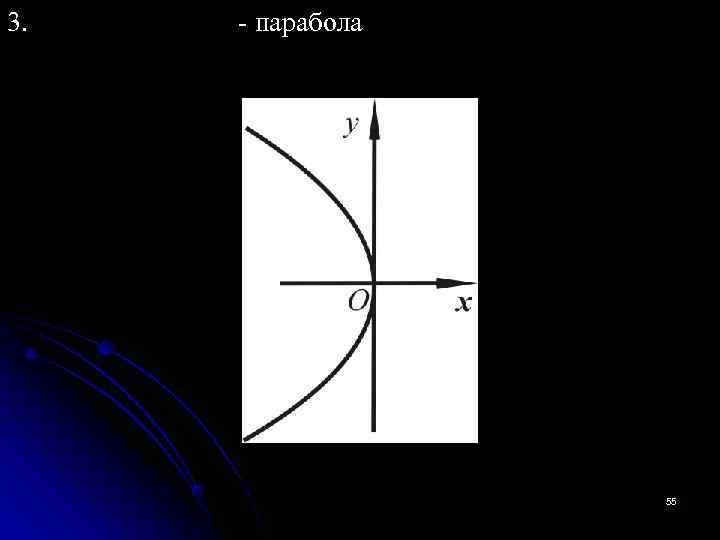
3. - парабола 55

4. Написать уравнение гиперболы, если известно, что точка лежит на гиперболе, один из фокусов находится в точке , а соответствующая директриса задана уравнением Решение. По директориальному свойству гиперболы: Пусть точка лежит на гиперболе. Тогда по директориальному свойству имеем 56

57