Кривые второго порядка Кривой второго порядка






















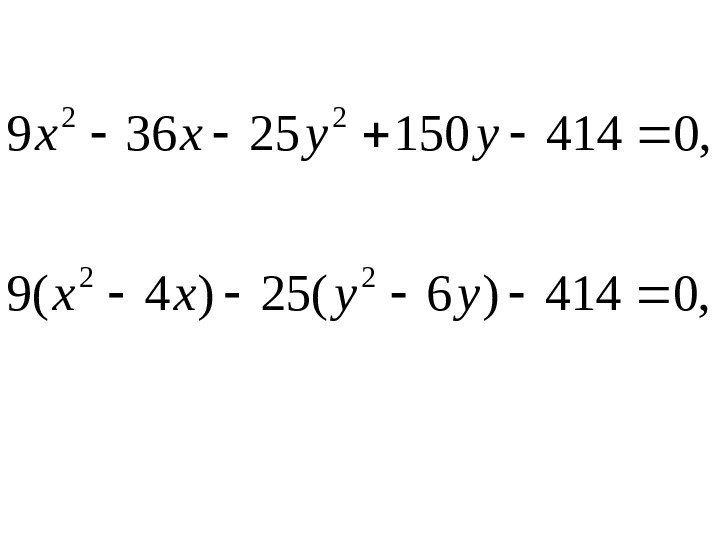
![, 0414]9)3[(25 ]4)2[(9 , 0414)3332(25 )2222(9 2 2 222 y x yy , 0414]9)3[(25 ]4)2[(9 , 0414)3332(25 )2222(9 2 2 222 y x yy](http://present5.com/presentforday2/20170124/analit_geo_2_images/analit_geo_2_27.jpg)
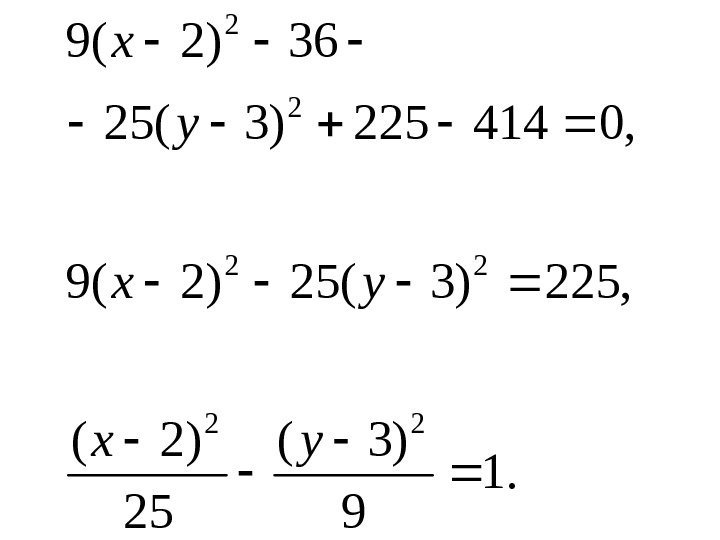


analit_geo_2.ppt
- Размер: 155.0 Кб
- Автор:
- Количество слайдов: 32
Описание презентации Кривые второго порядка Кривой второго порядка по слайдам
 Кривые второго порядка • Кривой второго порядка называется линия, уравнение которой в декартовой системе координат имеет вид, 0222 22 FEy. Dx. Cy. Bxy. Ax
Кривые второго порядка • Кривой второго порядка называется линия, уравнение которой в декартовой системе координат имеет вид, 0222 22 FEy. Dx. Cy. Bxy. Ax
 где коэффициенты А, В, С одновременно не обращаются в нуль. При А = В = С = 0 уравнение задаёт прямую, которая называется линией первого порядка. • К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.
где коэффициенты А, В, С одновременно не обращаются в нуль. При А = В = С = 0 уравнение задаёт прямую, которая называется линией первого порядка. • К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.
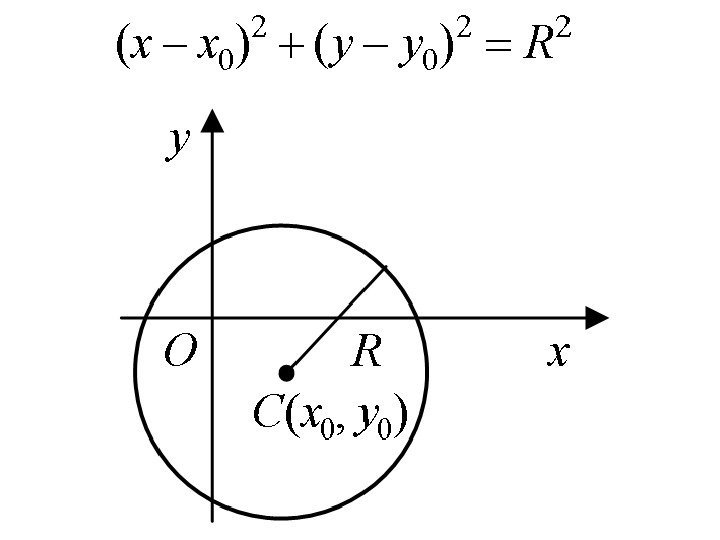
 • Окружностью называется множество точек плоскости, равноудаленных от данной точки (центра). • Если центр окружности поместить в начало координат, то каноническое уравнение окружности радиусом R имеет вид. 222 Ryx
• Окружностью называется множество точек плоскости, равноудаленных от данной точки (центра). • Если центр окружности поместить в начало координат, то каноническое уравнение окружности радиусом R имеет вид. 222 Ryx
 • Если центр окружности находится в точке C(x 0 , y 0 ) , то ее уравнение записывается в виде. )()( 22 0 Ryyxx
• Если центр окружности находится в точке C(x 0 , y 0 ) , то ее уравнение записывается в виде. )()( 22 0 Ryyxx

 • Пусть на плоскости заданы две точки F 1 и F 2 , расстояние между которыми равно 2 с, и задано число a > c.
• Пусть на плоскости заданы две точки F 1 и F 2 , расстояние между которыми равно 2 с, и задано число a > c.
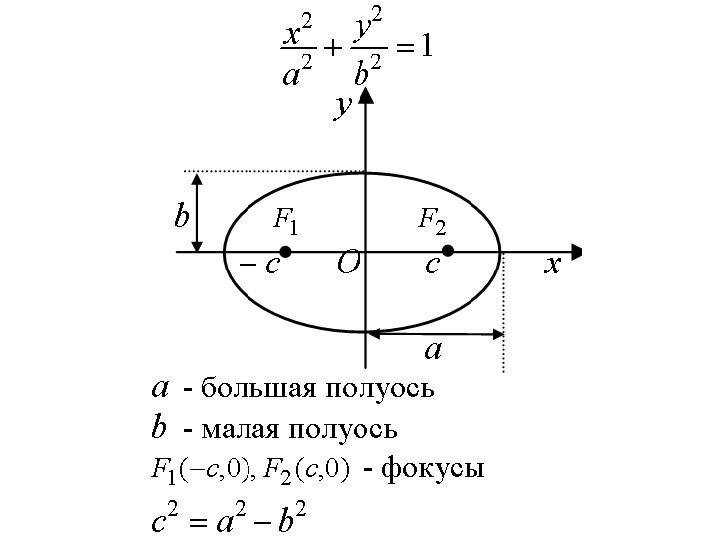
 • Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек F 1 и F 2 (фокусов) есть величина постоянная, равная 2 а.
• Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек F 1 и F 2 (фокусов) есть величина постоянная, равная 2 а.

 • Если систему координат выбрать так, как указано на рис. , то каноническое уравнение эллипса запишется в виде где а – большая, b – малая полуоси эллипса (при a > b ). , 1 2 2 b y a x , 222 cab
• Если систему координат выбрать так, как указано на рис. , то каноническое уравнение эллипса запишется в виде где а – большая, b – малая полуоси эллипса (при a > b ). , 1 2 2 b y a x , 222 cab
 • Фокусы эллипса расположены в точках F 1 (-c; 0) и F 2 (c; 0). • Окружность есть частный случай эллипса при a = b.
• Фокусы эллипса расположены в точках F 1 (-c; 0) и F 2 (c; 0). • Окружность есть частный случай эллипса при a = b.
 • Пусть на плоскости заданы две точки F 1 и F 2 , расстояние между которыми равно 2 с , и задано число a < c.
• Пусть на плоскости заданы две точки F 1 и F 2 , расстояние между которыми равно 2 с , и задано число a < c.
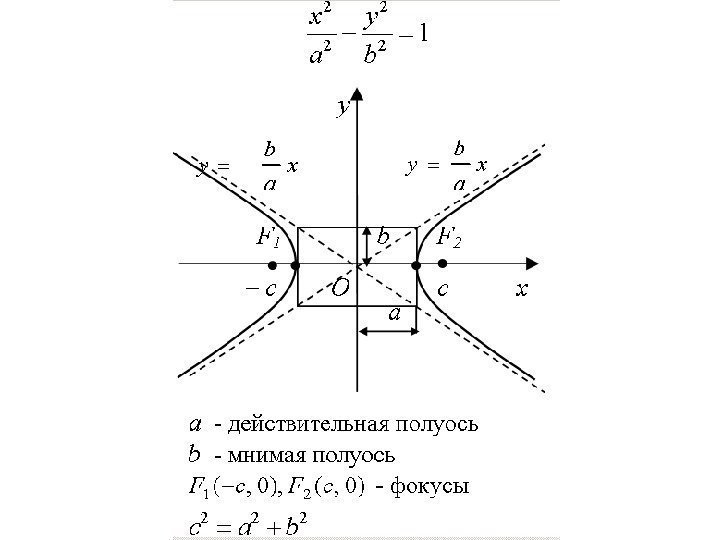
 • Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек F 1 и F 2 (фокусов) есть величина постоянная, равная 2 а.
• Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек F 1 и F 2 (фокусов) есть величина постоянная, равная 2 а.

 • Если систему координат выбрать так, как указано на рис. , то каноническое уравнение гиперболы запишется в виде • где • а – действительная, b – мнимая полуоси гиперболы. , 1 2 2 b y a x , 222 acb
• Если систему координат выбрать так, как указано на рис. , то каноническое уравнение гиперболы запишется в виде • где • а – действительная, b – мнимая полуоси гиперболы. , 1 2 2 b y a x , 222 acb
 • Гипербола состоит из двух ветвей и расположена симметрично относительно координатных осей. При этом ее ветви при удалении в бесконечность как угодно близко подходят к прямым которые называются асимптотами гиперболы. , x a b y
• Гипербола состоит из двух ветвей и расположена симметрично относительно координатных осей. При этом ее ветви при удалении в бесконечность как угодно близко подходят к прямым которые называются асимптотами гиперболы. , x a b y
 • При построении гиперболы вначале строят основной прямоугольник со сторонами x = ± a, y = ± b. Затем через противоположные вершины этого прямоугольника проводят прямые, которые являются асимптотами гиперболы.
• При построении гиперболы вначале строят основной прямоугольник со сторонами x = ± a, y = ± b. Затем через противоположные вершины этого прямоугольника проводят прямые, которые являются асимптотами гиперболы.
 • Вершины гиперболы расположены в точках с координатами ( – а, 0) и ( а, 0), а фокусы – в точках F 1 (-c; 0) и F 2 (c; 0).
• Вершины гиперболы расположены в точках с координатами ( – а, 0) и ( а, 0), а фокусы – в точках F 1 (-c; 0) и F 2 (c; 0).
 • Уравнение (или ) также задаёт гиперболу, сопряженную с гиперболой Действительная и мнимая полуоси этой гиперболы соответственно равны b и а. 1 2 2 2 2 b y a x 1 2 2 b y a x
• Уравнение (или ) также задаёт гиперболу, сопряженную с гиперболой Действительная и мнимая полуоси этой гиперболы соответственно равны b и а. 1 2 2 2 2 b y a x 1 2 2 b y a x
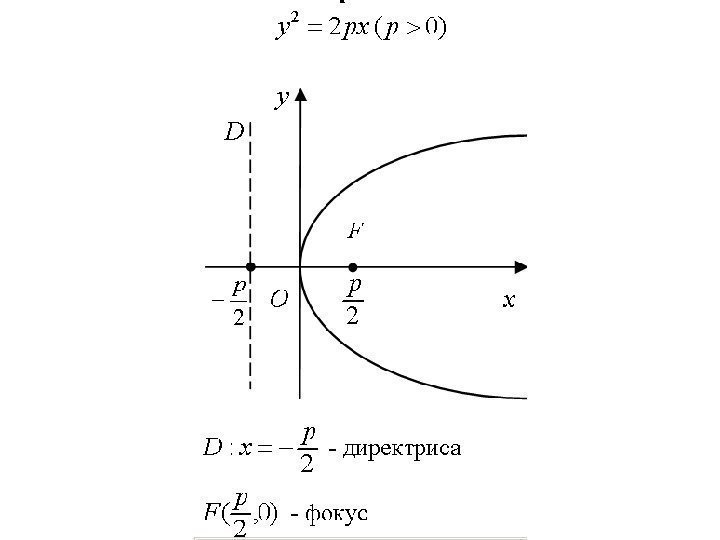
 • Пусть на плоскости задана точка F и прямая D , расстояние между которыми равно р. • Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой D (директрисы).
• Пусть на плоскости задана точка F и прямая D , расстояние между которыми равно р. • Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой D (директрисы).

 • Если систему координат выбрать так, как указано на рис. , то каноническое уравнение параболы запишется в виде. 2 2 pxy
• Если систему координат выбрать так, как указано на рис. , то каноническое уравнение параболы запишется в виде. 2 2 pxy
 • Эта парабола симметрична относительно оси Ох. Директрисой является прямая точка – фокус параболы, р – параметр параболы. , 2 p x 0, 2 p
• Эта парабола симметрична относительно оси Ох. Директрисой является прямая точка – фокус параболы, р – параметр параболы. , 2 p x 0, 2 p
 • Если p < 0, то парабола направлена в противоположную сторону. • Уравнение задаёт параболу, симметричную относительно оси Оу. pyx
• Если p < 0, то парабола направлена в противоположную сторону. • Уравнение задаёт параболу, симметричную относительно оси Оу. pyx
 • Для того, чтобы построить кривую второго порядка, заданную общим уравнением, уравнение кривой приводят к каноническому виду и переходят к новой системе координат.
• Для того, чтобы построить кривую второго порядка, заданную общим уравнением, уравнение кривой приводят к каноническому виду и переходят к новой системе координат.
 • Пример. Определить тип линии и схематически построить её: 041415036259 22 yxyx
• Пример. Определить тип линии и схематически построить её: 041415036259 22 yxyx
 • Решение. Приведем заданное уравнение к каноническому виду. Для этого в исходном уравнении выделим полные квадраты по переменным х и у. Перепишем исходное уравнение в виде:
• Решение. Приведем заданное уравнение к каноническому виду. Для этого в исходном уравнении выделим полные квадраты по переменным х и у. Перепишем исходное уравнение в виде:
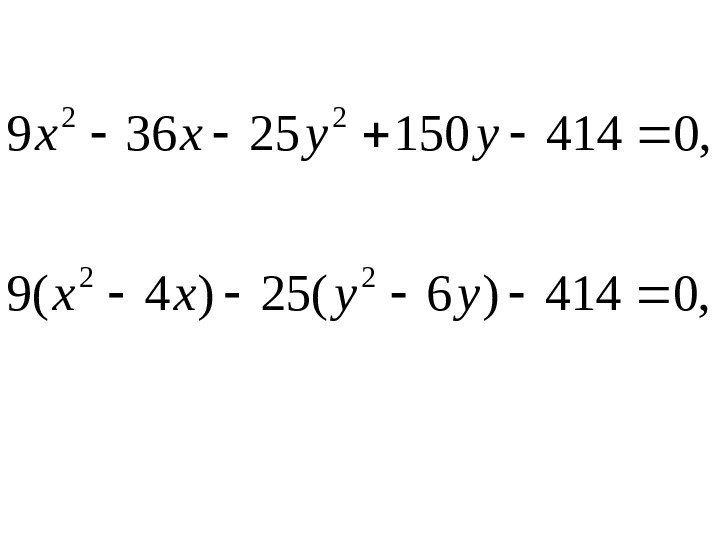 , 0414)6(25)4(9 , 041415025369 22 22 yyxx
, 0414)6(25)4(9 , 041415025369 22 22 yyxx
![, 0414]9)3[(25 ]4)2[(9 , 0414)3332(25 )2222(9 2 2 222 y x yy , 0414]9)3[(25 ]4)2[(9 , 0414)3332(25 )2222(9 2 2 222 y x yy](http://present5.com/presentforday2/20170124/analit_geo_2_images/analit_geo_2_27.jpg) , 0414]9)3[(25 ]4)2[(9 , 0414)3332(25 )2222(9 2 2 222 y x yy xx
, 0414]9)3[(25 ]4)2[(9 , 0414)3332(25 )2222(9 2 2 222 y x yy xx
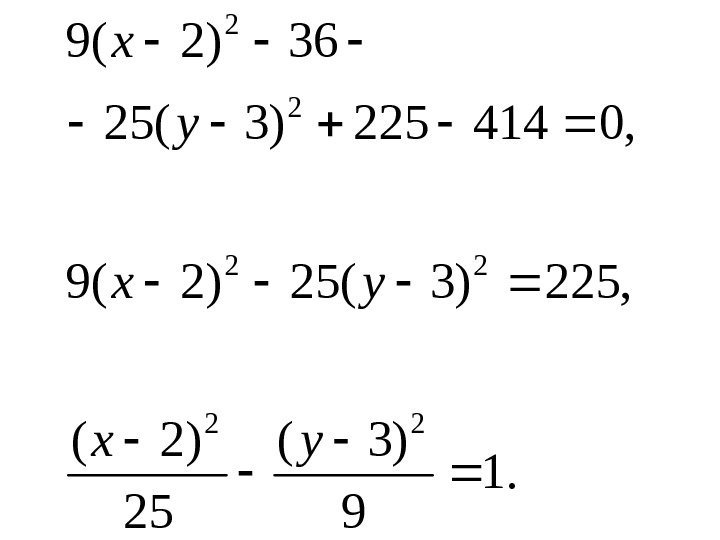 . 1 9 )3( 25 )2( , 225)3(25)2(9 , 0414225)3(25 36)2(9 22 22 2 2 yx yx y x
. 1 9 )3( 25 )2( , 225)3(25)2(9 , 0414225)3(25 36)2(9 22 22 2 2 yx yx y x
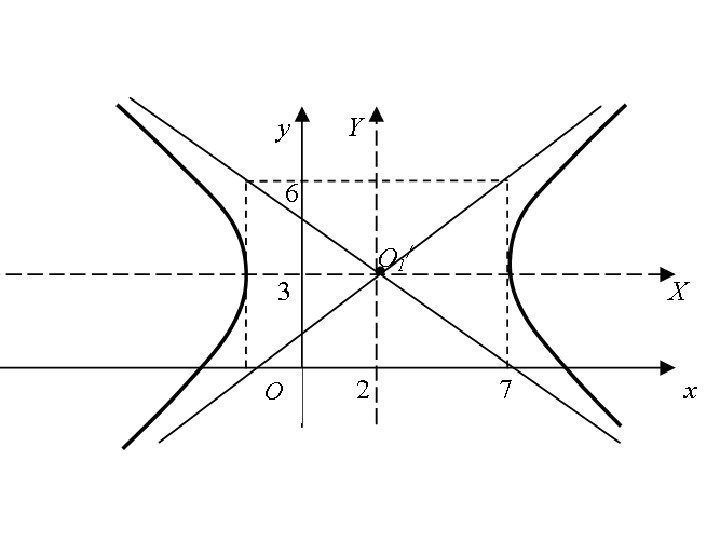
 • Совершим параллельный перенос координатных осей по формулам: (2, 3) – координаты центра O 1 системы координат X и Y. В этой системе координат уравнение принимает вид: . 3 , 2 y. Y x. X 1 925 22 YX
• Совершим параллельный перенос координатных осей по формулам: (2, 3) – координаты центра O 1 системы координат X и Y. В этой системе координат уравнение принимает вид: . 3 , 2 y. Y x. X 1 925 22 YX
 • Получили каноническое уравнение гиперболы (действительная полуось а = 5, мнимая полуось b =3)
• Получили каноническое уравнение гиперболы (действительная полуось а = 5, мнимая полуось b =3)

