КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ Криволинейная поверхность – непрерывное

КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ

Криволинейная поверхность – непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x, y, z) = 0.

КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ Криволинейные поверхности условно можно разделить на такие группы: • поверхности вращения, образованные вращением произвольной образующей вокруг неподвижной оси; • линейчатые поверхности, образованные движением прямой линии; в частности, винтовые поверхности, образованные движением прямой линии по винтовым направляющим; • поверхности второго порядка, которые перерезаются плоскостью по кривой второго порядка, - по кругу, эллипсу, параболе, гиперболе, и т. д. ; • циклические поверхности, образованные движением окружности; • топографические поверхности, которые не могут быть образованы за каким-либо простым законом и задаются на чертеже семейством некоторых линий (обычно линиями уровня).

ПРИМЕРЫ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ

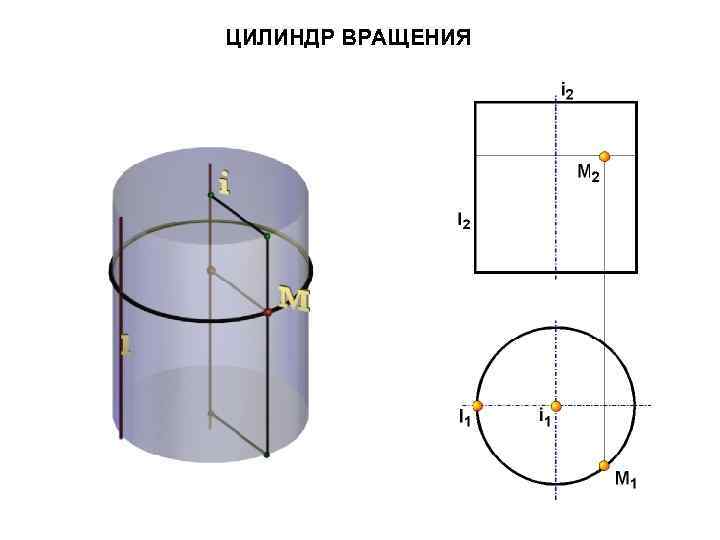ЦИЛИНДР ВРАЩЕНИЯ

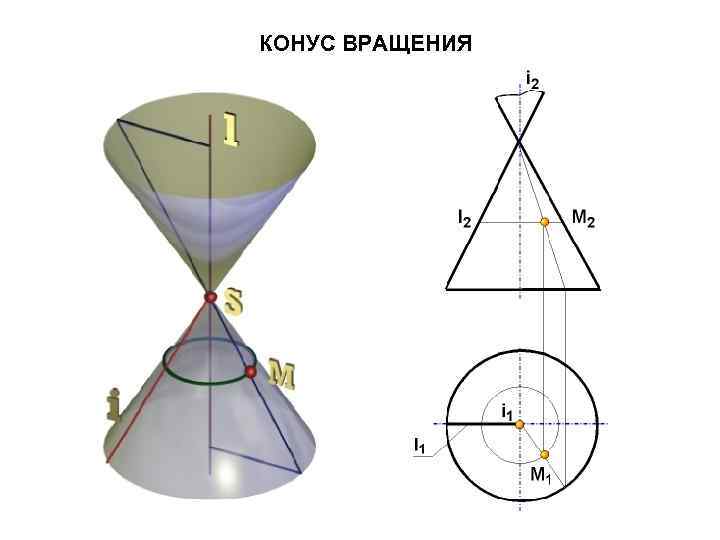КОНУС ВРАЩЕНИЯ

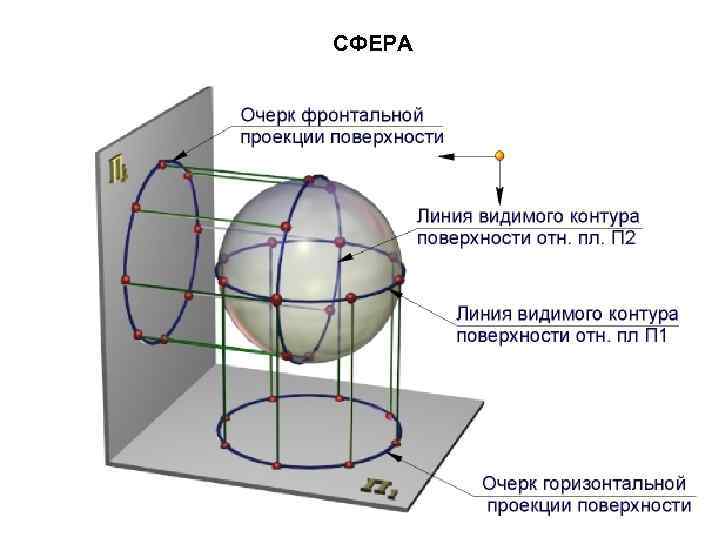СФЕРА

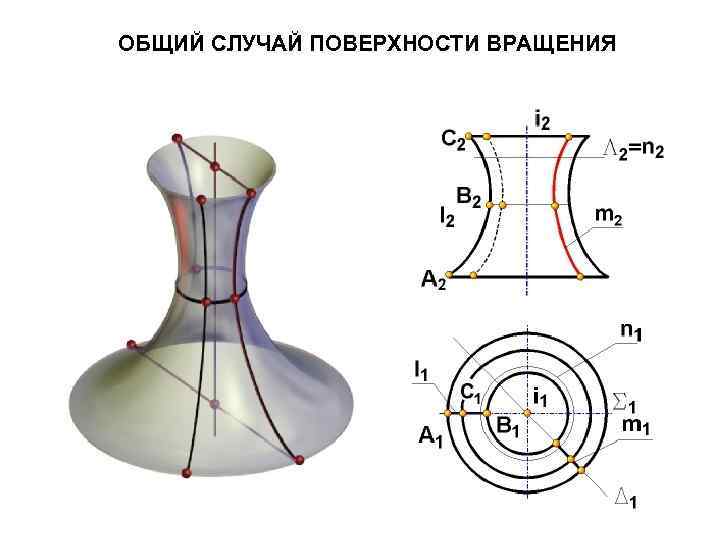ОБЩИЙ СЛУЧАЙ ПОВЕРХНОСТИ ВРАЩЕНИЯ

ПРИМЕРЫ ЛИНЕЙЧАТЫХ ПОВЕРХНОСТЕЙ

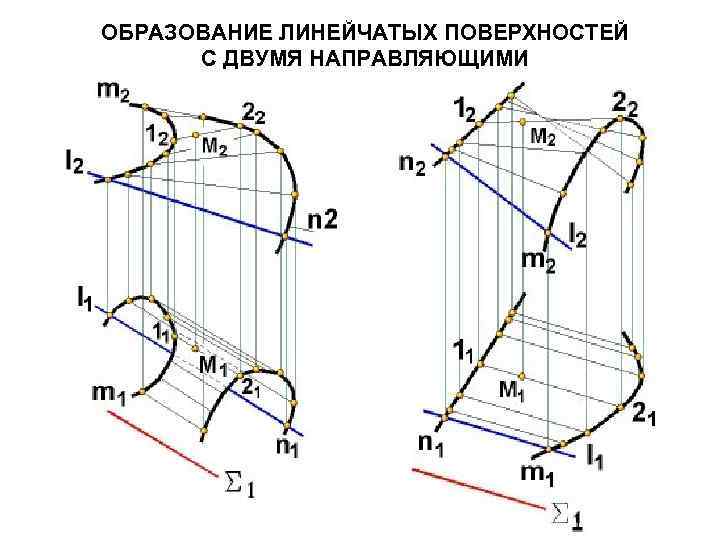ОБРАЗОВАНИЕ ЛИНЕЙЧАТЫХ ПОВЕРХНОСТЕЙ С ДВУМЯ НАПРАВЛЯЮЩИМИ

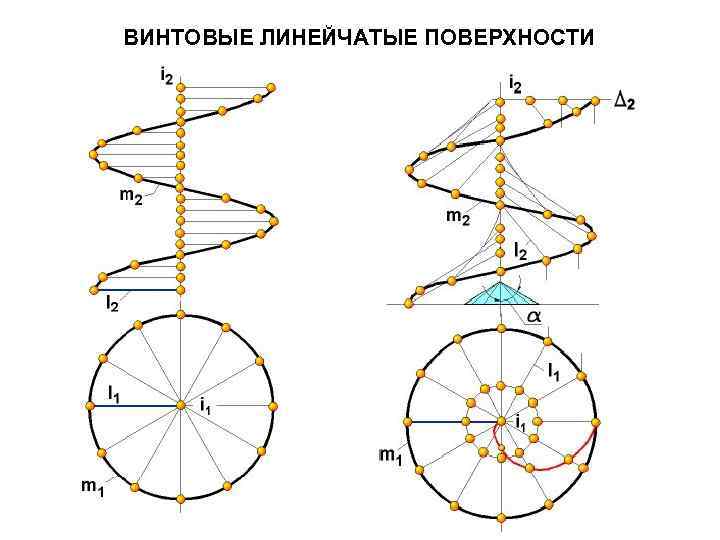ВИНТОВЫЕ ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ

ПРИМЕРЫ ПОВЕРХНОСТЕЙ 2 -ГО ПОРЯДКА

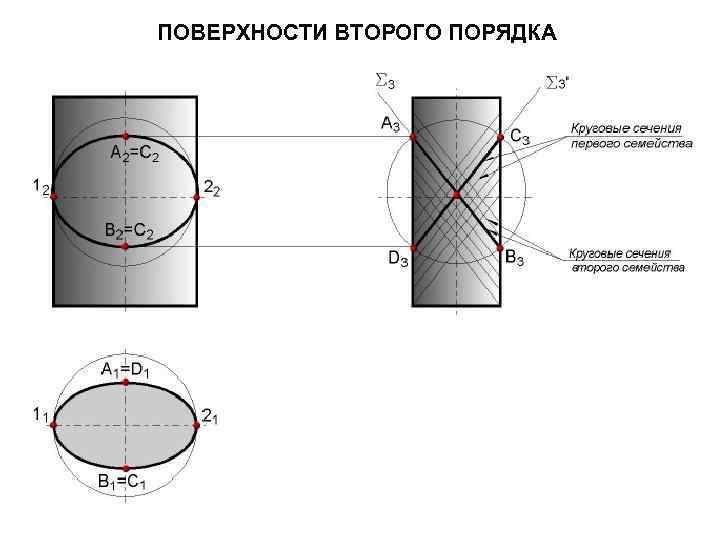ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

ПРИМЕР НЕЗАКОНОМЕРНОЙ (ТОПОГРАФИЧЕСКОЙ) ПОВЕРХНОСТИ